基于ABAQUS的JKM8330数控机床砂轮主轴有限元分析*

王成禹　王玉琢　邹世文　彭灵辉　胡建华　姚青青　姚海彪

(①清华大学航天航空学院，北京 100084；②江西杰克机床有限公司，江西 吉安 343008)



基于ABAQUS的JKM8330数控机床砂轮主轴有限元分析*

王成禹①王玉琢②邹世文②彭灵辉②胡建华②姚青青②姚海彪②

(①清华大学航天航空学院，北京 100084；②江西杰克机床有限公司，江西 吉安 343008)

应用Python语言实现对ABAQUS的二次开发，建立了JKM8330数控机床砂轮主轴的三维模型，采用弹簧单元模拟轴承支承的弹性支承边界条件，建立了砂轮主轴的动力学有限元分析模型，研究其在不同边界条件下的模态特性。通过参数化讨论的研究方法，深入研究了主轴振型对高速数控磨床加工精度的影响，获得了不同弹性支承刚度对主轴模态频率的影响规律。研究结果为高速数控磨床的结构优化设计提供了理论依据。

ABAQUS；砂轮主轴；弹性支承；模态分析；有限元

(①School of Aerospace, Tsinghua University, Beijing 100084, CHN;②Jiangxi JACK Machine Tool Co., Ltd., Ji’an 343008, CHN)

大功率高刚性高速主轴单元是实现高速高效高精磨削的关键，此类主轴单元目前主要应用在采用CBN砂轮磨削的凸轮轴高速精密加工装备中。随着我国汽车实施欧五排放标准的日益临近，大功率高刚性高速主轴单元的应用必将日益广泛。然而随着主轴单元转速的不断提高，所带来的问题也越来越突出，其动、静态性能对高速数控磨床的加工精度具有非常重要的影响[1]。为了提高高速数控磨床的加工精度、可靠性和加工性能，国内外学者对高速主轴等关键部件做了大量的研究工作[2-5]。

砂轮主轴在高速旋转的情况下，可能因砂轮主轴的不平衡严重影响加工精度，甚至引起配套液压轴承等关键部件的失效破坏。由于主轴单元在高速运转时产生的振动无法通过或者由于结构的原因不能通过在线动平衡的方式进行消减，所造成的后果是磨削表面质量的下降以及CBN砂轮耐用度的显著降低等。故为了消减高速振动除了需要提高主轴组件的支撑刚性和动平衡精度外，还有非常重要的一点是要对主轴组件本身的动态特性进行分析与优化设计，通过优化设计确定主轴组件支撑刚性的合理范围及动平衡精度，从而保证主轴单元高速运转的平稳性。

基于ABAQUS有限元分析软件建立了JKM8330数控机床砂轮主轴的动力学分析有限元模型，研究其不同边界条件下的振动模态特性。通过参数化讨论的方法，研究了不同弹性支承对主轴模态频率的影响，获得了主轴振型对高速数控磨床加工精度的影响规律。研究结果为高速磨床的结构改进设计提供了理论依据。

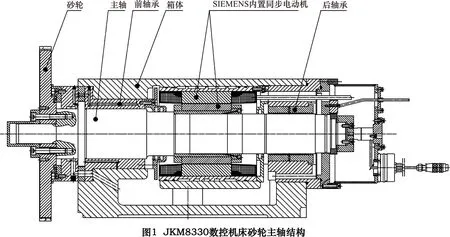
1　JKM8330数控机床砂轮主轴结构

以江西杰克机床有限公司自主研制生产的JKM8330数控机床高速砂轮主轴为研究对象。JKM8330高精度随动数控凸轮轴磨床采用了自主研发的高速高刚性液体动静压电主轴，可保证砂轮使用线速度达120 m/s以上，真正实现了高效磨削。砂轮架进给系统采用直线电动机直驱的高精度、高灵敏度响应圆柱静压导轨。所采用的多磨头磨削控制技术可在一次装夹中，通过自动切换不同尺寸的砂轮来完成工件异形复合面的高精度随动磨削。

该高速主轴单元是采用动静压轴承支撑的电主轴，电动机置于两静压轴承之间，主轴前支撑直径为100 mm，后支撑直径为80 mm，驱动电动机采用西门子内置电动机，电动机额定功率为34 kW，最大功率为50 kW，主轴单元最高转速可达8 500 r/min，额定工作转速为6 600 r/min，在额定工作转速下可保证直径350 mm的CBN砂轮(砂轮宽度≤60 mm)在120 m/s的线速度下实现高速高效高精度磨削，结构简图如图2所示。主轴动静压轴承支撑的静态刚度在500 N/μm以上，动态刚性在1 000 N以上。

2　有限元分析模型

2.1高速砂轮主轴有限元模型的建立

高速砂轮主轴单元主要由转轴、轴承、电动机和壳体组成，这里只考虑转轴和轴承部分。ABAQUS有限元分析软件是一款目前应用最广的动、静力学分析软件之一，应用Python语言实现对ABAQUS的二次开发，建立高速砂轮主轴的有限元分析模型，如图3所示。

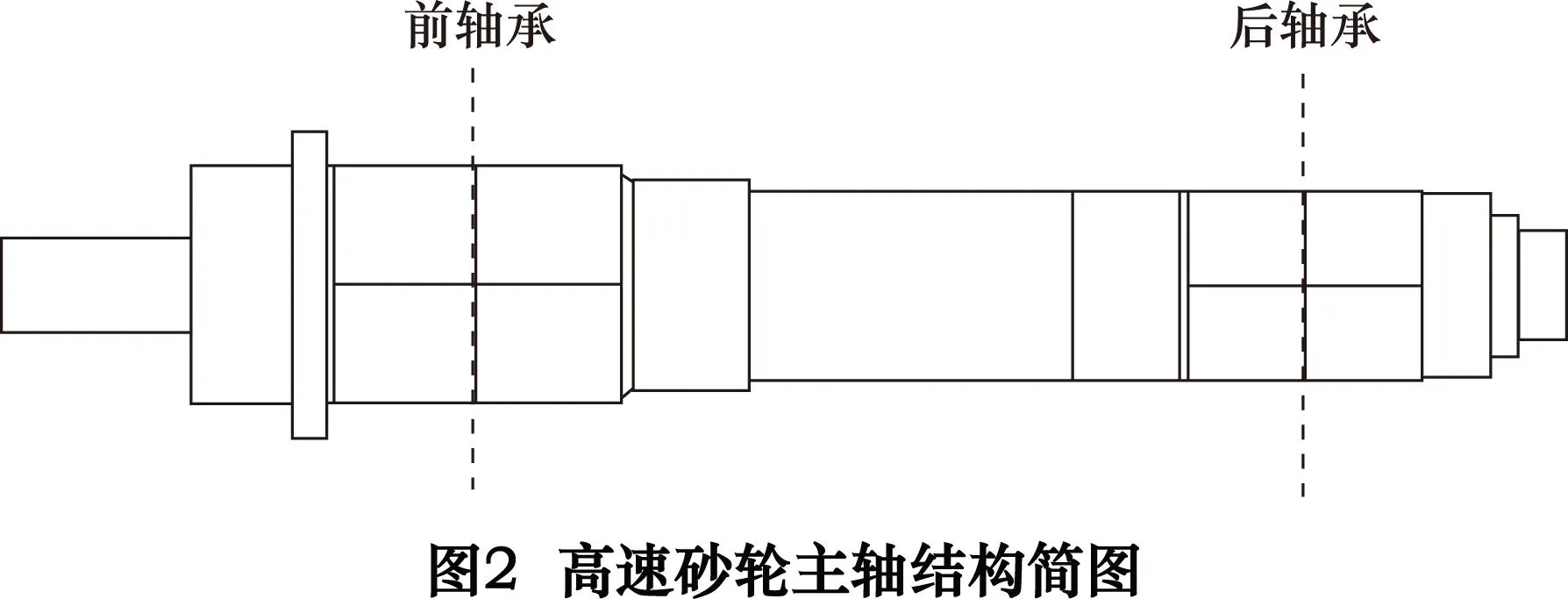
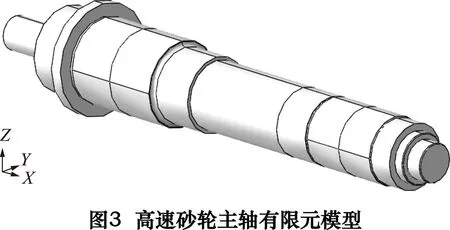
对于有限元分析计算，网格划分对计算结果影响较大。为了获得准确的计算模拟结果，对模型进行了精细的网格划分，共生成523 450个C3D4实体单元，如图4所示。

2.2材料属性及边界条件

该高速主轴单元的材料是38CrMoAlA合金钢，具体性能参数如表1所示。

表138CrMoAlA合金钢的性能参数

E/MPaμΡ/(kg/m3)2100000.37800

基于主轴单元的有限元模型，合理施加边界条件是准确获得力学响应的重要保证。根据实际情况可知，主轴的支承并不是刚性的，在进行分析时应该考虑轴承的弹性性能影响。由于砂轮主轴的轴向刚度非常大，将动静压轴承简化为只具有径向刚度的弹性支承边界，支点位置如图5所示，每个弹性支承均由4个均布的弹簧组成[6]。

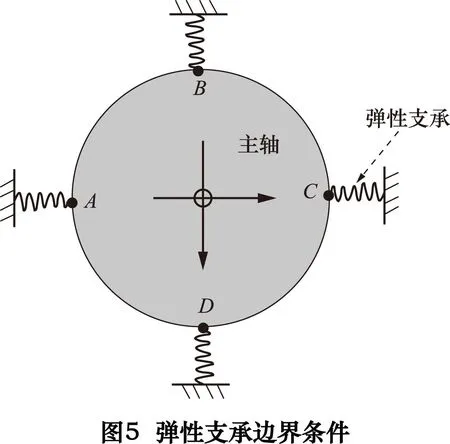
如图5所示，为了限制主轴的轴向刚体运动，在前轴承处与弹簧相连接的4个主轴上的节点(ABCD)上施加轴向位移约束，而在弹簧另一端施加完全约束，即约束所有自由度。

3　数值模拟结果与讨论

采用参数化讨论的研究方法，研究主轴振型对高速数控磨床加工精度的影响，深入探究不同轴承弹性支承刚度对主轴模态频率的影响规律。

3.1主轴振型对高速数控磨床加工精度的影响

为了确定高速砂轮主轴结构的振动特性，需要对其进行准确的模态分析[7-9]。JKM8330数控机床砂轮主轴前后轴承的弹性支承刚度分别为Kfore=500 N/μm和Kback=300 N/μm。采用Block Lanczos方法计算了主轴的振动响应，并提取了前9阶振动模态，这里给出前9阶振型云图，如图6所示，表2给出了对应的固有频率计算结果。

根据表2，可以看出：砂轮主轴的1阶固有振动频率等于0，即表征主轴在圆周方向具有刚体转动特性，可以忽略；第2阶与第3阶固有频率非常接近，并且从图6中可以看出两阶振型表现为正交，可将其视为一对重根；同理，第4阶与第5阶和第6阶与第7阶均是频率相近，振型正交；然而，第8阶振型表现为主轴轴向拉伸特性；第9阶振型表现为主轴前后两端的转动特性。

由公式(1)可以计算得到主轴的临界转速，如表2所示。

n=60·f

(1)

式中：n为主轴临界转速，r/min；f为主轴模态频率。

为了保证数控机床的运行安全和加工精度要求，机床在工作时的砂轮主轴的最高转速不能超过最小临界转速的75%，即不能超过53 418×75%=40 063.5 r/min，而JKM8330数控机床砂轮主轴最高转速为8 500 r/min，远远小于要求的临界转速。因此，在该种条件下，砂轮主轴可以有效地避开共振区域，保证数控机床的运行安全和相应的加工精度要求。

如图6所示，砂轮主轴主要以弯曲变形为主要振型特性，同时也有轴向拉伸变形和主轴头部与尾部的转动。为了保证砂轮主轴的磨削加工精度，主轴的综合变形不允许超过极限值。

综上分析，可以得出：该型砂轮主轴的设计刚度远远大于要求值，因此，可以通过进一步优化设计，改善主轴性能，节约成本，提高主轴的可靠性。

3.2弹性支承刚度对主轴模态频率的影响规律

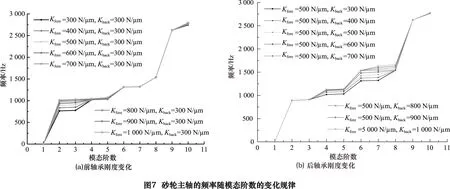
为了研究轴承弹性支承刚度对主轴模态频率的影响，采用参数化讨论的方法，获得了弹性支承刚度对主轴模态频率的影响规律，如图7所示。

图7a给出了在后轴承弹性支承刚度不变的情况下，前轴承弹性支承刚度的变化对主轴各阶模态频率的影响曲线。如图所示，对于主轴的前2～5阶固有频率，随着Kfore的增加而逐渐增大，但第2阶和第3阶固有频率对Kfore产生的变化更加敏感，这说明了Kfore的变化对前5阶固有频率具有非常重要的影响；然而，当主轴模态阶数大于6阶之后，随着Kfore的变化，主轴模态频率的变化非常小，这说明仅仅通过调整前轴承的弹性支承刚度不能够明显地改变主轴的高阶频率。

如图7b所示，在前轴承弹性支承刚度不变的情况下，随着后轴承弹性支承刚度的变化，中间阶数的主轴模态频率产生明显的变化。可以看出，第3～8阶主轴模态频率随后轴承弹性支承刚度的增加而逐渐增大；然而，后轴承弹性支承刚度的变化对第1～3阶和第8～10阶频率的影响非常小，这说明了通过改变后轴承弹性支承刚度可以较好的控制主轴的中间阶数频率，而对较低阶和较高阶频率的总体作用不大。

表2砂轮主轴模态频率及临界转速

阶数123456789频率/Hz0890.3908.751018.910321313.31322.41539.42624.2临界转速/(r/min)053418545256113461920787987934492364157452

综上所述，可以在一定程度上通过调整前后轴承弹性支承刚度来控制主轴的模态频率，进而减小主轴的振动对数控磨床磨削加工精度的影响。

4　结语

应用Python语言实现对ABAQUS的二次开发，建立了JKM8330数控机床砂轮主轴的动力学有限元分析模型，研究其在不同边界条件下的振动模态特性。通过参数化讨论的研究方法，深入研究了主轴振型对高速数控磨床加工精度的影响，获得了不同弹性支承刚度对主轴模态频率的影响规律，得出结论如下：

(1)该型主轴的第2阶和第3阶固有频率对前轴承弹性支承刚度产生的变化更加敏感，而仅仅通过调整前轴承的弹性支承刚度不能够明显地改变主轴的高阶频率。

(2)后轴承弹性支承刚度的改变对主轴中间阶数频率的影响较大，而对较低阶和较高阶频率的总体作用不大。

(3)计算得到了该型主轴的重要模态参数，为进一步结构改进设计提供了理论基础。

[1]Zhang Y M, Lin X L, Wang X D, et al. The study on the dynamic characteristic of high speed machine tool and experiment validate[J]. Advances in Materials Manufacturing Science and Technology, 2004, 471/472: 571-576.

[2]Krulewich A K. Temperature integration model and measurement point selection for thermally induced machine tool errors[J].Mechatronics, 1998(8): 395-412.

[3]Ramesh R, Mannan M A, Poo A N. Support vector machines model for classification of thermal error in machine tools[J]. Advanced Manufacturing Technology, 2002, 20: 112-120.

[4]Lin C W, Tu J F, Kamman J. An integrated thermomechanical dynamic modal to characterize motorized machine tool spindles during very high speed rotation[J].International Journal of Machine Tool & Manufacturing, 2003, 43: 1035-1050.

[5]赵中太, 陈波. 浅谈高速机床的振动[J]. 制造技术与机床, 2010(2):45-46.

[6]梁双翼, 陈晨, 尹辉俊. 基于有限元方法的电主轴模态分析[J]. 制造业自动化, 2012(34): 57-60.

[7]韩益建. 数控机床的振动故障分析[J]. 制造技术与机床, 2009(5):134-135.

[8]李芳芳, 贾平, 宁怀民. 基于ANSYS的某型号丝杠的模态分析[J]. 机械设计与制造, 2011(11): 61-62.

[9]刘丹萍, 蒋占四, 冯建国, 等. 机床主轴的SolidWorks建模与有限元分析[J]. 机床与液压, 2013(41): 123-125.

(编辑汪艺)

如果您想发表对本文的看法，请将文章编号填入读者意见调查表中的相应位置。

Finite element analysis of JKM8330 CNC machine grinding wheel spindle based on ABAQUS

WANG Chengyu①, WANG Yuzhuo②, ZOU Shiwen②, PENG Linghui②, HU Jianhua②, YAO Qingqing②, YAO Haibiao②

The three-dimensional model of JKM8330 CNC machine grinding wheel spindle is established based on ABAQUS. The spring elements are adopted to simulate the elastic support boundary conditions. The dynamic mechanics finite element analysis model for grinding wheel spindle is proposed to study the modal characteristics for different boundary conditions. A numerical parametrical study is conducted to discuss the effect of the main shaft vibration mode on the machining precision of high speed CNC grinding machine, and the influence law of the elastic support stiffness on the spindle modal is obtained. It is signif-icant to Provide theoretical references for the structure optimization design of high speed grinding machine.

ABAQUS; grinding wheel spindle; elastic support; modal analysis; FEM

TP391.9

A

王成禹，男，1987年生，博士研究生，主要研究方向是轻质复合材料动静力学性能研究，已发表论文7篇。

2015-08-12)

160320

*国家科技重大专项项目(2015ZX04002022-004)