基于啮合接触分析下的斜齿轮齿面滑动摩擦因数的计算*

王　成

(①北京工业大学机械工程与应用电子技术学院，北京 100124；②济南大学机械工程学院，山东 济南 250022)



基于啮合接触分析下的斜齿轮齿面滑动摩擦因数的计算*

王成①②

(①北京工业大学机械工程与应用电子技术学院，北京 100124；②济南大学机械工程学院，山东 济南 250022)

根据Xu推导出的齿面滑动摩擦因数计算公式，利用斜齿轮副啮合接触分析的相关结果，对斜齿轮齿面滑动摩擦因数进行计算。首先，通过斜齿轮副轮齿接触分析和承载接触分析，得到齿面啮合点的法向载荷、传动误差、接触点位置和接触线长度。其次，将法向载荷带入赫兹公式得到最大接触应力。将传动误差带入齿面啮合点速度计算公式，最终得到齿面啮合点的滑动速度和卷吸速度。最后，将所有参数带入齿面滑动摩擦因数计算公式，得到一对斜齿轮轮齿从进入啮合到退出啮合齿面接触点的滑动摩擦因数。以一对斜齿轮传动为例，利用上述方法计算得到齿面接触点的滑动摩擦因数，与Xu得出的结论进行对照，结果合理。

斜齿轮；滑动摩擦因数；啮合接触分析

齿面滑动摩擦因数是齿面摩擦特性研究的重要内容。准确计算啮合齿面的滑动摩擦因数，对于减少齿轮啮合摩擦损失、增大轮齿承载能力和改善齿轮系统传动性能等方面具有重要意义。

齿面滑动摩擦因数的计算方法分为以弹流润滑理论为基础和以齿面摩擦特性试验为基础2类[1]。通常对于齿面滑动摩擦因数的处理，一种是用平均滑动摩擦因数代替齿面啮合点的滑动摩擦因数[2-5]。而据试验结果表明，齿面滑动摩擦因数与齿面啮合点的滑动速度、卷吸速度、润滑油粘度、载荷、曲率半径和表面粗糙度等有关。第二种来自于试验公式，显然他们比第一种方法更加准确，但这些公式均取自于特定的试验环境，如润滑类型、温度、速度、载荷和表面粗糙度等，而这些可能与使用者的实际计算环境存在差异。第三种是对试验公式的改进，使它们应用范围更广。但这些公式假定轮齿承受理想载荷，没有考虑齿轮修形、支撑变形等情况。此外，有些公式存在较多问题[6-7]。例如，齿轮在节点附近啮合时，其滑动速度趋向0，即接近纯滚动。这时，滑动摩擦因数应该接近于0。而利用这些公式得到的结果往往过大。

Xu[8-9]根据文献[1]中的非牛顿热弹性润滑理论，推导出弹流润滑状态下的直齿轮和斜齿轮齿面滑动摩擦因数计算公式，与相关的试验结果对照，能很好的符合。Xu得出的相关结论包括：(1)目前的滑动摩擦因数计算公式得出的结果一般较大；(2)齿轮在节线附近啮合时，滑动摩擦因数接近于0；(3)齿面啮合点的滑动速度和卷吸速度之比的绝对值越小，滑动摩擦因数越小。

Xu所推导的公式如下，

(1)

(2)

式中：μ为滑动摩擦因数；SR为齿面啮合点的滑动速度Vs和卷吸速度Ve之比，SR=vs/ve，r为齿面啮合点的综合曲率半径，r=r1r2/(r1+r2)，r1和r2为两齿轮齿面啮合点的曲率半径；Ph为最大接触应力；v0为润滑油的动力粘度，cPs；s为微粗糙度，μm；bi为与齿轮润滑油相关的常数，文献[8-9]中采用一种常用的齿轮润滑油(75W90)，bi(i=1, 2, …, 9)=(-8.92，1.03,1.04，-0.35,2.81，-0.10,0.75，-0.39,0.62)。

Kolivand[10]在此基础上，对弧齿锥齿轮和准双曲面齿轮的齿面滑动摩擦因数进行了计算。

Xu和Kolivand在计算齿面接触点滑动速度和卷吸速度时，仅考虑了齿轮啮合的几何关系，未考虑承载传动误差的存在，而承载传动误差是表征受载情况下被动轮实际转角偏离理论转角的数值。因此，本文利用Litvin[11-12]的齿轮啮合接触分析理论，基于Xu推导出的齿面滑动摩擦因数计算公式，对斜齿轮齿面滑动摩擦因数进行精确计算，其计算流程见图1。

1　斜齿轮副几何接触分析(tooth contact analysis-TCA)和承载接触分析(loaded Tooth contact analysis-LTCA)

1.1斜齿轮副几何接触分析TCA

图2为一对斜齿轮副啮合的坐标关系，当一对齿轮接触时，两齿面的接触点有公共位置矢量和公共法线矢量。即，斜齿轮副的几何接触分析可用下式表示：

(3)

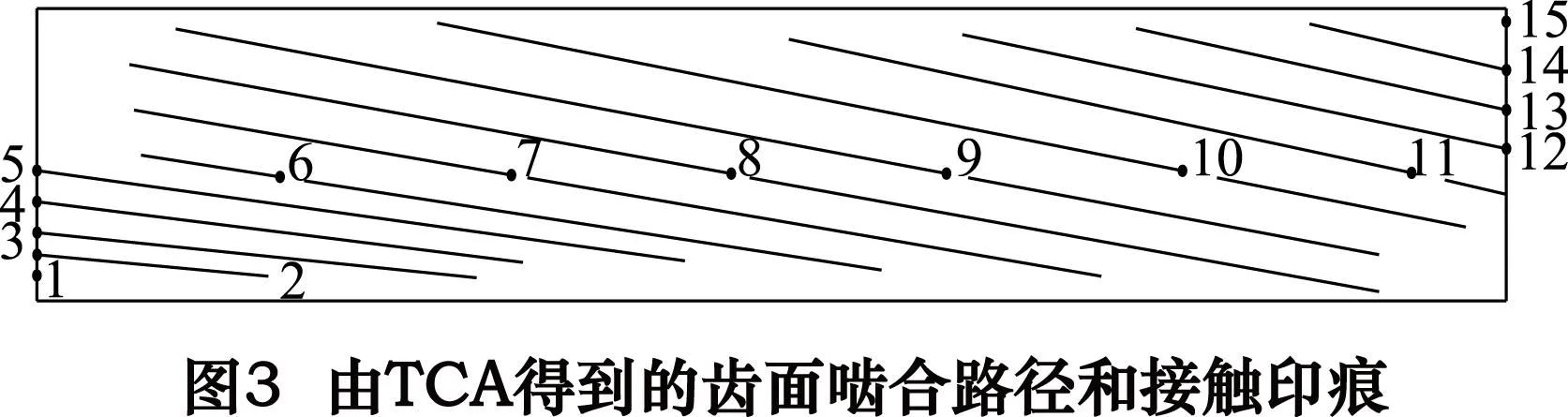
第二个矢量方程是由单位矢量组成，因此，式(3)包括5个方程。该方程中有6个参数，以小轮转角φ1为已知量，按一定步长赋值，可以得到另外5个参数值。齿轮边缘接触的求解方法类似，只是参数变为了5个，同样以小轮转角φ1为已知量，按一定步长赋值，可以得到另外4个参数值。斜齿轮TCA的求解具体可以参见文献[12]，通过TCA的求解，可得到齿面啮合路径和接触印痕。图3为某斜齿轮副通过TCA计算后得到的齿面啮合路径和接触印痕。

1.2斜齿轮副承载接触分析LTCA

斜齿轮副在受载时，瞬时接触点变为椭圆，而椭圆长轴远大于短轴，因此承载接触分析放在长轴上进行。根据轮齿受载前后的变形关系，斜齿轮副的承载接触分析可用下式表示：

(4)

其中：Xj(j=1,2,…,2n+1)为人工变量，[X]=[X1,X2, …,X2n]T；[λ]为主、被动轮接触椭圆长轴离散点处的柔度矩阵；[F]为离散点载荷；[d]为啮合点处变形后的法向齿面间隙；F为总法向载荷；[w]为啮合点处初始法向齿面间隙；[Z]为轮齿变形后的法向位移。

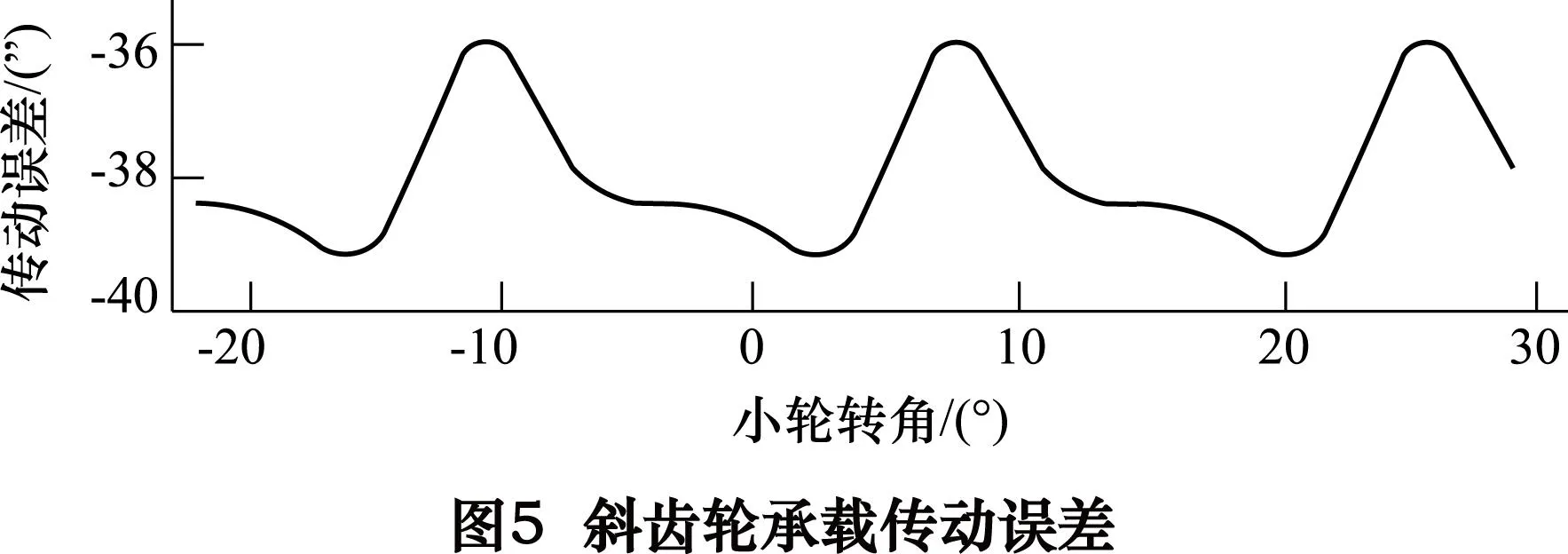
利用有限元柔度矩阵的非线性规划法可以对方程(4)进行求解[13]，通过LTCA的求解，可得到齿面载荷分布和承载传动误差。图4和图5为某斜齿轮副通过LTCA计算后得到的齿面载荷分布和承载传动误差。

1.3齿面啮合点法向载荷的计算

根据LTCA的计算结果，可以求得一对轮齿从啮入到啮出任意啮合位置接触点i上的法向载荷Fi(图6)，其可表示为[5]：

(5)

其中：n为接触点i处椭圆长轴离散点j的个数，pj为离散点所受的法向载荷。

1.4接触位置接触线长度的计算

根据离散点的法向载荷可以得到该接触位置接触线的长度。以图6为例，如果计算得到的p1=0，p2>0，pn>0，则实际接触线的长度为离散点p2和pn之间的距离。

2　齿面滑动摩擦因数计算公式中相关参数的计算

2.1齿面啮合点滑动速度和卷吸速度的计算

Sheng[14]利用齿轮啮合的几何关系得到齿面接触点的滑动速度和卷吸速度。在此基础上，我们考虑传动误差的影响，以此计算被动轮的实际转角值。

在图7中，轮1为主动轮，轮2为从动轮。轮1和轮2在啮合点i处的齿面切向速度V1(i)、V2(i)为

v1(i)=ω1ri1sin(αi1)

(6)

v2(i)=ω2(i)ri2sin(αi2)

(7)

(8)

式中：ω1为轮1的角速度；ω2(i)为轮2在啮合位置i处的角速度；Δω(i)为啮合位置i处的承载传动角速度误差；Z1、Z2分别为轮1、轮2的齿数；αi1、αi2分别为轮1、轮2车啮合点i的压力角，αik=arccos(rbk/rik)，k=1、2(1为轮1、2为轮2)；rb1、rb2为轮1、轮2的基圆半径；ri1、ri2为轮1、轮2上啮合点i至回转中心o1、o2的距离。

通过LTCA可得到轮1和轮2啮合接触点的角度误差，为将其转化为角速度误差，涉及到的时间计算如下：

(9)

式中：t表示轮1转过相邻瞬时接触点所需的时间；N是一对斜齿轮轮齿从啮入到啮出齿面瞬时接触位置(点)的个数；Δφi是主、从动轮齿面瞬时接触点的角度误差。

轮1和轮2齿面啮合点的滑动速度Vs(i)为：

vs(i)=v1(i)-v2(i)

(10)

轮1和轮2齿面啮合点的卷吸速度Ve(i)为：

(11)

随着啮合位置的变化，αi1和αi2不断变化，在节点上，αi1=αi2，其滑动速度趋向0(若不考虑传动误差，则滑动速度为0)，即接近纯滚动。

2.2最大接触应力的计算

最大接触应力Ph可近似地用赫兹公式来表示：

(12)

式中：W′为沿齿面接触线单位长度上的平均载荷，W′=F/l，l为接触线的长度(即LTCA中所求得的椭圆长轴的长度)；F为接触点(椭圆长轴)的法向载荷；r为齿面接触点的综合曲率半径；E′为等效杨氏模量值。

(13)

在齿轮设计中引入的弹性系数ZE，

(14)

将式(13)和(14)代入式(12)，得

(15)

3　算例

以一对斜齿轮传动为例，这对斜齿轮的参数见表1。齿轮的材料均为铸钢，弹性系数ZE=188.0。齿轮润滑油的参数见表2。

表1斜齿轮传动的参数

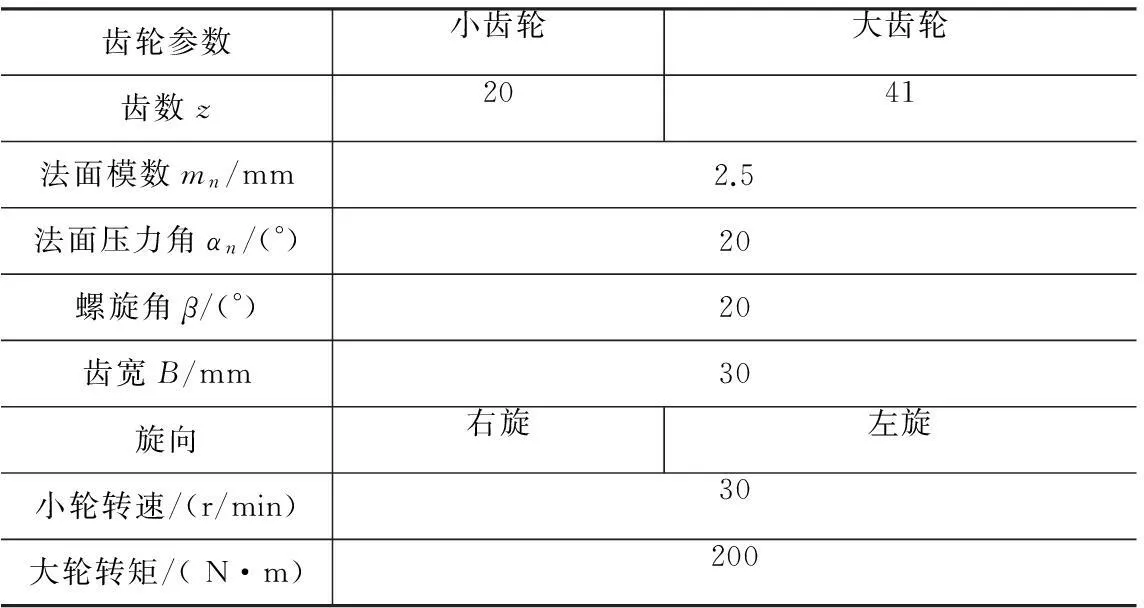
齿轮参数小齿轮大齿轮齿数z2041法面模数mn/mm2.5法面压力角αn/(°)20螺旋角β/(°)20齿宽B/mm30旋向右旋左旋小轮转速/(r/min)30大轮转矩/(N·m)200

表2齿轮润滑油的参数(测量温度100 ℃)

参数测量值密度ρ/(kg/L)0.78运动粘度υ/cSt14.31

运动粘度υ的国际单位是m2/s，动力粘度v0的国际单位是Pa·s。文中所给单位为非国际单位，它们之间的关系如下，

1 Pa·s=1 N·s/m2=103cPs

(16)

1 cSt=1 mm2/s

(17)

因此，齿轮油的动力粘度v0为，

v0=ρv=0.78/10-3×(14.31×10-6)×103=11.2cPs

(18)

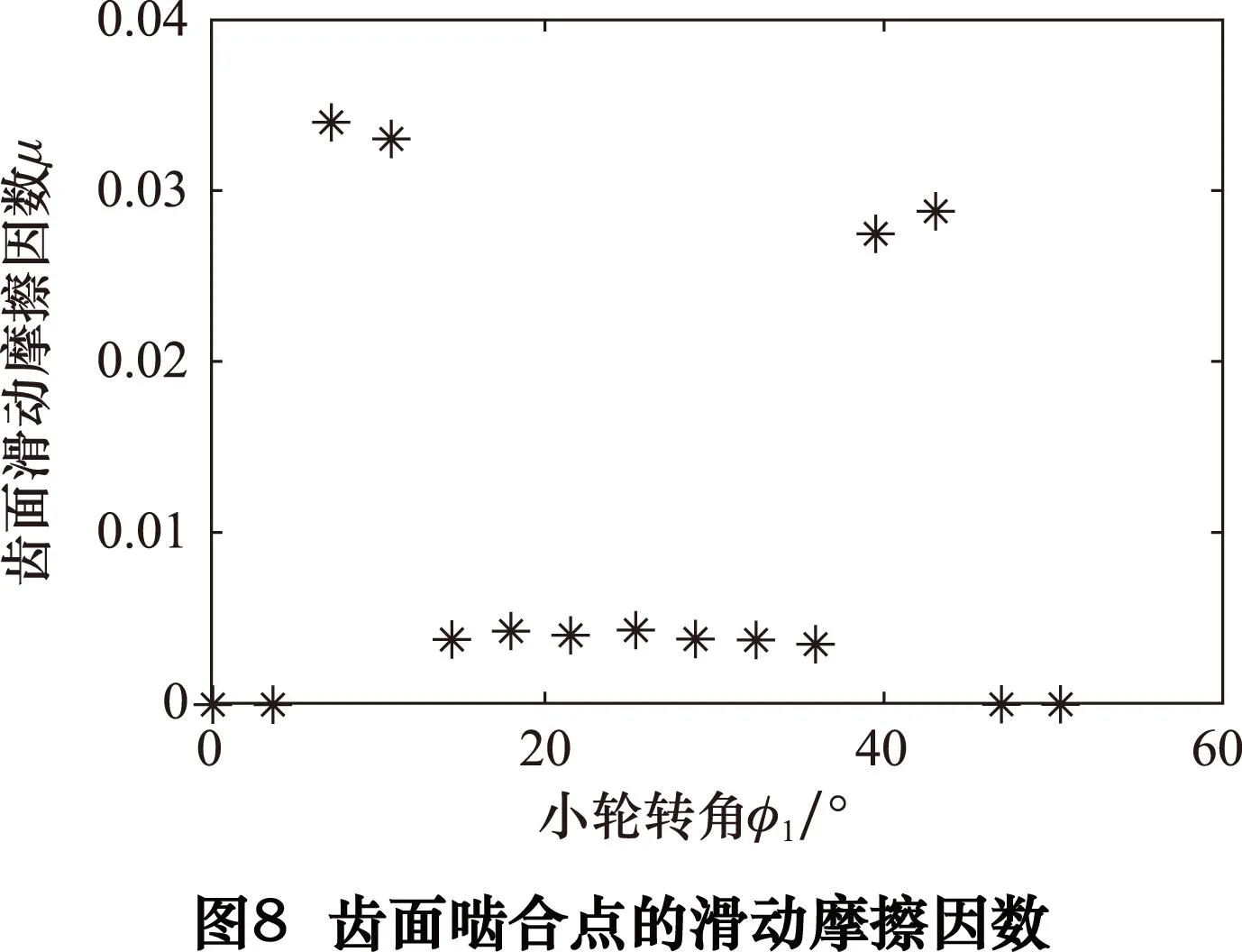
斜齿轮副TCA和LTCA的计算结果分别见图3、4、5和表3。将它们分别带入式(3)～(18)，得到式(1)和式(2)中的相关参数，进而得到一对斜齿轮轮齿从进入啮合到退出啮合齿面接触点的滑动摩擦因数以及滑动摩擦因数与齿面啮合点的滑动速度和卷吸速度之比SR的关系(图8和图9)。

从图8和图9中可以看出：(1)齿面接触点的滑动摩擦因数较小，符合文献[8-9]中的相关结论。(2)齿轮节点附近滑动摩擦因数接近于0，这符合齿轮在节点附近啮合，其滑动速度趋向0，即接近纯滚动。这时，滑动摩擦因数应该接近于0的结论。(3)齿面啮合点的滑动速度和卷吸速度之比的绝对值越小，滑动摩擦因数越小，这符合文献[8-9]中的相关结论。

4　结语

利用斜齿轮副轮齿接触分析TCA和承载接触分析LTCA的相关结果，计算得到齿面啮合点的最大接触应力、滑动速度、卷吸速度、接触线长度和综合曲率半径等相关参数。带入Xu推导的齿面滑动摩擦因数计算公式中，得到一对斜齿轮轮齿从进入啮合到退出啮合齿面接触点的滑动摩擦因数。以一对斜齿轮传动为例，利用上述方法计算得到齿面接触点的滑动摩擦因数，结果表明合理。啮合齿面滑动摩擦因数的准确计算，对于减少齿轮啮合摩擦损失、增大轮齿承载能力和改善齿轮系统传动性能等方面具有重要意义。

表3斜齿轮副TCA和LTCA的计算结果

位置结果δϕ/(”)r/mml/mmF/N138.5125.100238.8525.3700338.8325.694.78130436.0726.14.75568537.9226.67.151575638.5126.69.542523738.8526.614.333468838.8326.614.3333861936.0726.614.3335841037.9226.611.9425771138.5126.69.5416281238.8526.864.776841338.8327.482.3841611436.0728.17001537.9228.9300

[1]Cioc C, Cioc S, Moraru, L, et al. A deterministic elastohydrodynamic lubrication model of high-speed rotorcraft transmission components [J]. Tribol. Trans., 2002, 45(4): 556-562.

[2]Heingartner P, Mba D. Determining power losses in the helical gear mesh; case study [C]. Proceeding of DETC’3, ASME 2003 Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Chicago, Illinois, 2003.

[3]Pedrero J I. Determination of the efficiency of cylindrical gear sets[C]. 4th World Congress on Gearing and Power Transmission, Paris, France, 1999.

[4]Michlin Y, Myunster V. Determination of power losses in gear transmissions with rolling and sliding friction incorporated [J]. Mechanism and Machine Theory, 2002, 37: 167-174.

[5]王成, 高常青, 贾海涛. 基于人字齿轮啮合特性的滑动摩擦功率损失的研究[J]. 中南大学学报, 2012,43(6):2173-2178.

[6]Drozdov Y N, Gavrikov Y A. Friction and scoring under the conditions of simultaneous rolling and Sliding of bodies [J]. Wear, 1967, 11(4): 291-302.

[7]O’Donoghue J P, Cameron A. Friction and temperature in rolling sliding contacts [J]. ASLE Trans., 1966, 9(2): 186-194.

[8]Xu H. Development of a generalized mechanical efficiency prediction methodology for gear pairs [D]. Ph.D. Dissertation, Ohio State University, Columbus, Ohio, 2005.

[9]Xu H, Anderson N E, Maddock D G Kahraman. Prediction of mechanical efficiency of parallel-axis gear pairs [J]. Journal of Mechanical Design, 2007, 129(1): 58-68

[10]Kolivand M, Li S, Kahraman A. Prediction of mechanical gear mesh efficiency of hypoid gear pairs [J]. Mechanism and Machine Theory, 2010, 45(11): 1568-1582.

[11]Litvin F L. Gear geometry and applied theory [M]. PTR Prentice Hall, Englewood Cliffs, New Jersey 07632, USA, 1994.

[12]Litvin F L, Lu Jian, Townsend D O, et al. Computerized simulation of meshing of conventional helical involute gears and modification of geometry [J]. Mechanism and Machine Theory, 1999, 34: 123-147.

[13]Shuting Li. Gear contact model and loaded tooth contact analysis of a three-dimensional, thin-rimmed gear [J]. Journal of Mechanical Design, 2002, 124(3):511-517.

[14]Sheng Li, Ahmet Kahraman.Prediction of spur gear mechanical power losses using a transient elastohydrodynamic lubrication model [J]. Tribology Transactions, 2010, 53 (4), 554-563.

(编辑孙德茂)

如果您想发表对本文的看法，请将文章编号填入读者意见调查表中的相应位置。

Calculation of sliding friction coefficients of helical gears based on the contact analysis

WANG Cheng①②

(①College of Mechanical Engineering and Applied Electronics Technology, Beijing University of Technology,Beijing 100124, CHN; ②School of Mechanical Engineering, University of Jinan, Jinan 250022, CHN)

According to the sliding friction coefficient formula proposed by Xu, the sliding friction coefficients of tooth surface are calculated based on the effects of meshing contact analysis of helical gears. Firstly, the normal forces, the transmission errors, the position of contact points and the length of contact line are obtained from tooth contact analysis (TCA) and loaded tooth contact analysis (LTCA) of helical gears. Secondly, the normal forces are substituted into the Hertz formula, the maximum contact stresses are calculated. The transmission errors are substituted into the calculation formula of speed, the sliding velocity and rolling velocity of contact points on tooth surface are calculated. Finally, all parameters are substituted into the formula of sliding friction coefficient, the sliding friction coefficient from gear-into gear-out are obtained. Illustrated by an example of a pair of helical gears, the sliding friction coefficients of contact points are obtained by the above methods. Compared with the conclusion obtained by Xu, the effects are reasonable.

helical gears; sliding friction coefficient; meshing contact analysis

TH132

A

王成，男，1977生，在职博士后，讲师，主要从事机械传动等方面的研究。

2015-07-21)

160310

*国家自然科学基金(51475210)；山东省优秀中青年科学家科研奖励基金(BS2011ZZ002)； 中国博士后科学基金(2014M550577)；北京市博士后工作经费(2014ZZ-27)