基于FDE-SVR的非线性系统辨识

王鲜芳，张 帅

（河南师范大学 计算机与信息工程学院，河南 新乡453007）

基于FDE-SVR的非线性系统辨识

王鲜芳，张 帅

（河南师范大学 计算机与信息工程学院，河南 新乡453007）

针对非线性系统辨识中模型难以确定的问题，提出一种基于FDE-SVR（Fuzzy Differential Evolution Support Vector Regression，FDE-SVR）的非线性系统辨识方法。论文首先使用FDE自动获取SVR的相关参数；然后，使用FDE-SVR进行非线性系统辨识；最后，验证FDE-SVR辨识得到的非线性系统模型。仿真实验表明：FDE-SVR辨识可以忽略模型的具体结构，辨识得到的模型具有较高的精度，最终验证该模型的泛化性。

系统辨识；支持向量机；模糊集；差分进化

0　引言

在实际工业生产过程中，大部分系统是非线性的，如果想要准确地控制一个非线性系统，就要对非线性系统的模型进行辨识，才能实施控制或者故障诊断［1-2］。传统的线性系统辨识理论尽管比较成熟，但难以在非线性系统中应用，因此设计一种针对非线性系统智能辨识方法尤为重要。

基于支持向量回归机 （Support Vector Regression）的非线性系统识别是一种新兴的辨识方法，能够有效地处理非线性、高维数据，并且具有较强的泛化能力。这些特点使得SVR非常适合于非线性系统辨识。王文栋［3］等提出了基于SVR的控制系统辨识建模研究，吴德会［4］利用SVR来进行非线性动态系统的辨识。但是SVR参数的确定过程比较繁琐和困难，针对参数确定困难的问题，本文提出了基于FDE的SVR参数选择方法，并用该方法得到的最优参数进行非线性系统辨识。

基于FDE-SVR的非线性系统辨识的主要步骤：首先使用FDE自动获取SVR最优相关参数；得到最优参数以后，把最优参数代入SVR中进行非线性系统辨识；辨识得到相应的非线性系统模型后，使用典型信号验证得到基于 FDE-SVR的非线性系统模型；最后通过仿真实验证明该设计的有效性。

1　基于FDE-SVR的非线性系统辨识原理

基于SVR的非线性系统辨识的结构详细为：

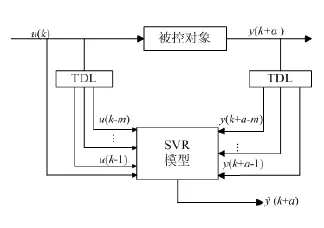
图1 基于SVR的结构框架

图1中，m为输入延迟，n为输出延迟，α为系统输出对输入的总时延数，且一般情况下，u为控制系统的辨识信号 y为控制系统的输出信号，ŷ为SVR辨识的SVR模型M的输出，TDL为多分头时延系统。辨识目的就是用SVR模型代替被控制对象得到ŷ，作为被控对象的输出。

1.1SVR基本原理

支持向量机（Support Vector Machine，SVM）是Corinna Cortes和Vapnik［5］于20世纪90年代中期首先提出的一种统计学习理论。支持向量回归机［6］（Support Vector Regression，SVR）是后来在SVM的基础上通过引入不敏感损失函数的概念应用到回归拟合问题中，回归问题研究的是根据已知的输入样本值估计与之对应的输出值。假设给定样本训练集

收稿日期：2016-04-10

基金项目：国家自然科学基金（5201119120003）；河南省高校创新人才支持计划项目（2012HASTIT011）

作者简介：王鲜芳（1969―），女，河南洛阳人，教授，主要从事生化过程建模、故障诊断、机器学习等研究。

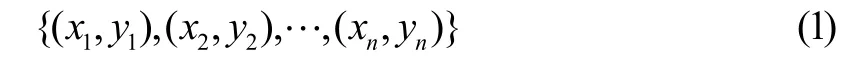
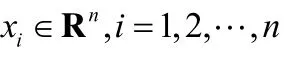
SVR形式表示：

其中，wT是权向量，w∈RK，b∈R是偏置向量常数。依据该结构风险最小化原则，式（2）的SVR优化目标函数为

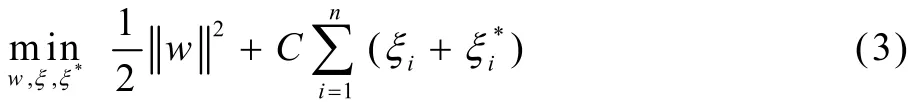
约束条件：

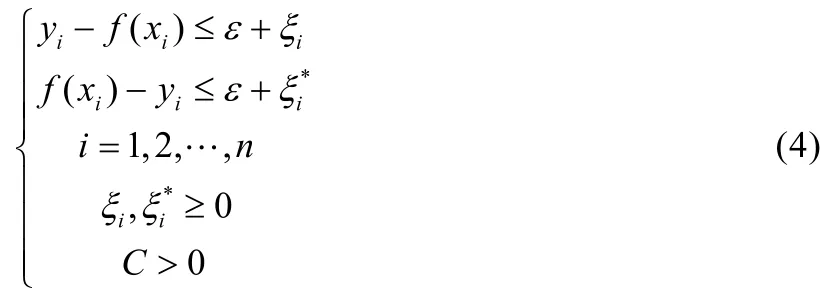
非线性SVR的回归函数形式为：

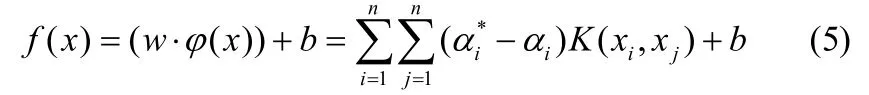
使用高斯核函数的SVR有三个参数：惩罚系数C、核参数σ和不敏感损失函数ε。惩罚系数C表示对样本误差的惩罚程度，影响模型的泛化能力。核参数σ决定样本分布在高维空间中的复杂程度。不敏感损失函数ε忽略实际值与估计值间的误差掉，对特定区间的误差是不敏感，一般选择为0.1，0.01 和0.001，本文选择为0.001。

1.2基于FDE的SVR参数选取

由于SVR的参数的确定是一个复杂的过程，所以引入模糊集［7］中隶属度函数，将模糊集概念引入到差分进化算法（Differential Evolution， FD）［8］中提出了一个用使用模糊差分进化算法（Fuzzy Differential Evolution， FDE）来自动获取SVR的参数。具体做法：

（1）输入变量与输出变量的量化

输入变量DEn/N、Kgn/N（N代表总的进化代数），变化范围分别为（0，1］、（0.02，0.1）；输出变量为kF和kCR；变化范围分别为［0.97，1.02］、［0.97，1.02］。变量的量化等级分为三级［1，2，3］，量化情况如表1所示

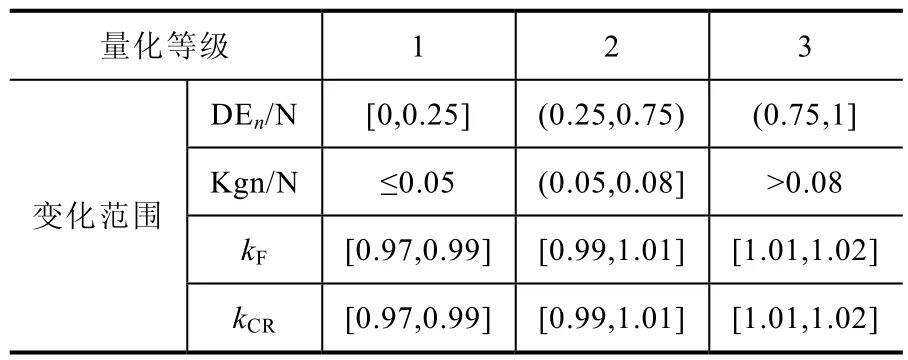
表1　模糊变量的量化值

（2）模糊集合的隶属度函数

对于输入变量DEn/N、Kgn/N、kF、kCR采用数值法描述它们的模糊集合的隶属度函数，如表2所示：

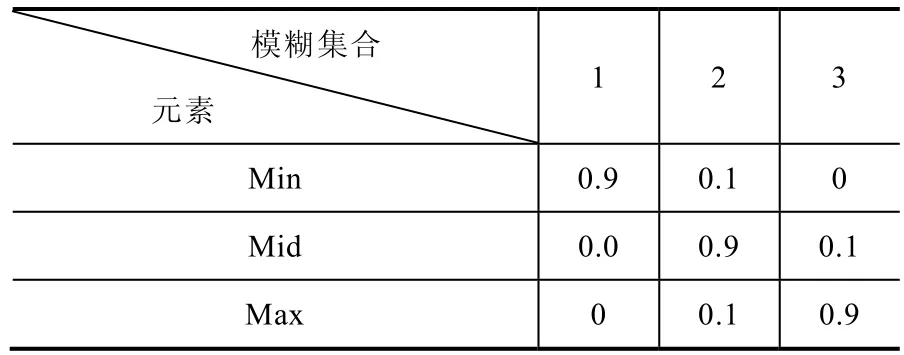
表2　变量模糊集合隶属度函数

（3）模糊推理规则

根据以上影响差分进化调节因子的模糊分析，可以得到模糊差分进化优化过程中对进化算子调整的推理规则。具体如表3所示：

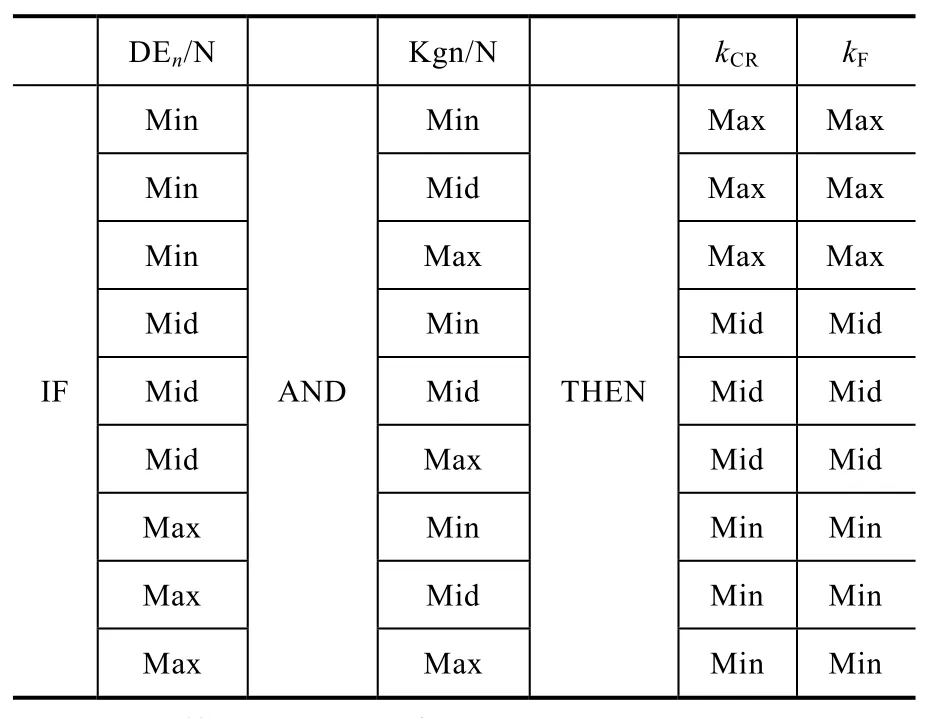
表3　模糊推理准则

（4）模糊变量的清晰化

由表3模糊推理得到的是模糊量，而实际控制必须为清晰量，因此需要将模糊量kF和kCR清晰化，以方便后续步骤的计算。该论文采用随机法，从相应的范围中随机选择。

综上所述模糊差分进化算法具体实现过程为：

（1）生成初始群体

在n维实数空间中按（6）式产生满足条件的个体，具体方法为：

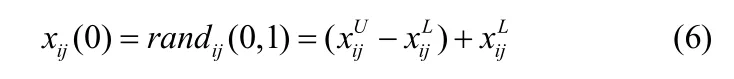
（2）变异操作

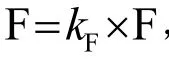
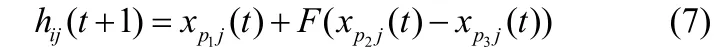
如果无局部优化问题，则变异操作可写为

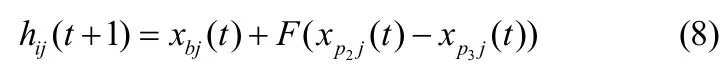
（3）交叉操作

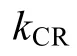
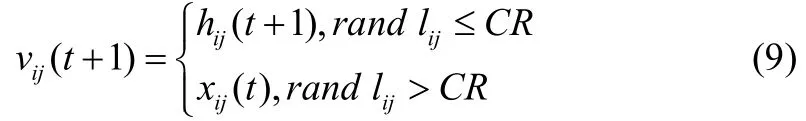
（4）选择操作

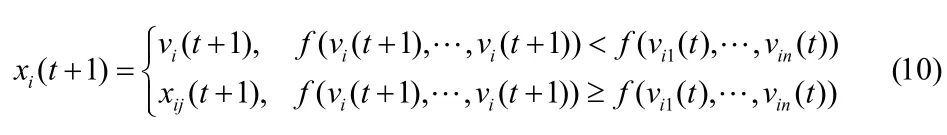
（5）判断是否达到最大进化次数如果达到则结束，输出SVR需要选择的参数C，σ2，否则返回步骤（2）继续进化。

1.3FDE-SVR非线性系统辨识流程

在非线性系统辨识中，非线性系统模型的结构难以确定。因此，论文主要使用 FDE-SVR来模拟逼近非线性系统模型，优点是：避开确定非线性系统模型结构，实现非线性系统辨识。该过程中，论文基于 FDE-SVR进行非线性系统辨识的主要思想为：使用FDE自动获取SVR的相关参数，然后用FDE-SVR来进行非线性系统辨识；最后，验证辨识出的系统模型。

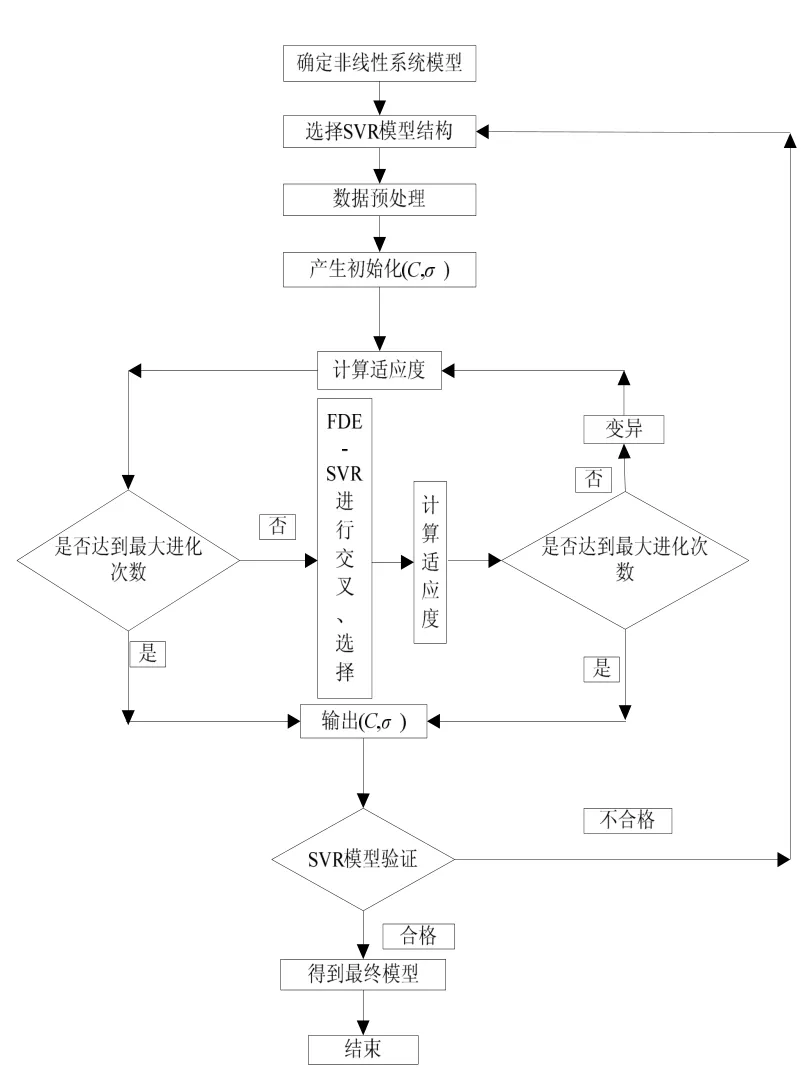
图2　FDE-SVR非线性系统辨识一般步骤

2　仿真实验

2.1仿真模型选择及辨识目的

该论文以（11）式为被辨识对象，进行仿真研究。

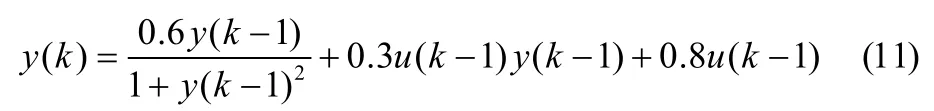
辨识的目的：使最终目标使辨识得到的辨识模型和系统与实际输出差值最小，为此定义适度函数：

2.2数据来源及样本选择

则设计模型（11）的训练样本为：

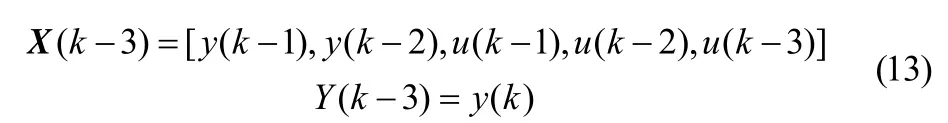
采样时间为0.01s和仿真时间为2s。系统辨识信号采用幅值为2的随机信号。SVR参数选择：输入向量为：

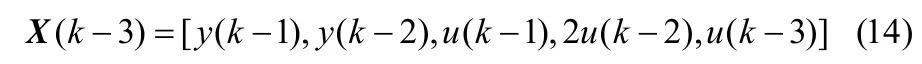
输出为：

2.3基于FDE的SVR参数范围

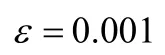
2.4辨识结果及分析

为了说明 FDE-SVR在寻优参数时的优势，分别使用FDE和DE进行参数寻优实验。

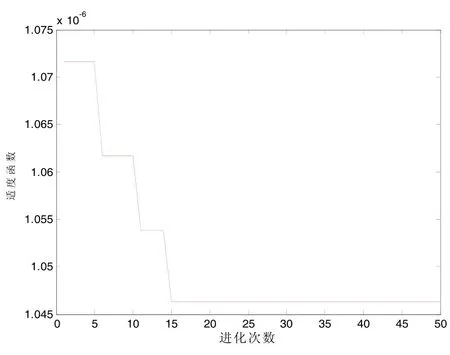
图3　DE-SVR适度函数变化图

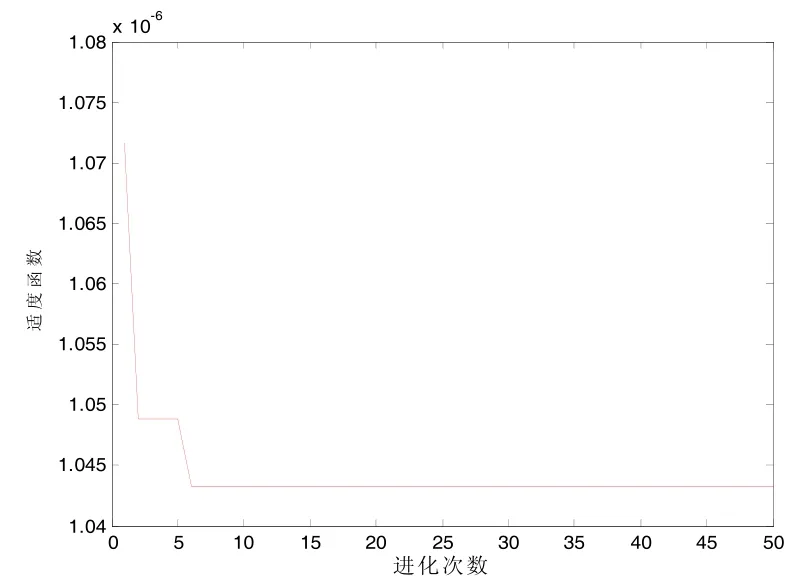
图4　FDE-SVR适度函数变化图

对比图（3）DE-SVR适度函数变化图与（4）FDE-SVR适度函数变化图可以得出改进后的差分进化算法比典型的差分进化算法在寻找 SVR的参数上具有明显的趋势。改进后的差分进化算法在寻找最优参数的时，经过6代就可以找到最优参数。而标准差分算法在经过19代左右才找到最优参数。

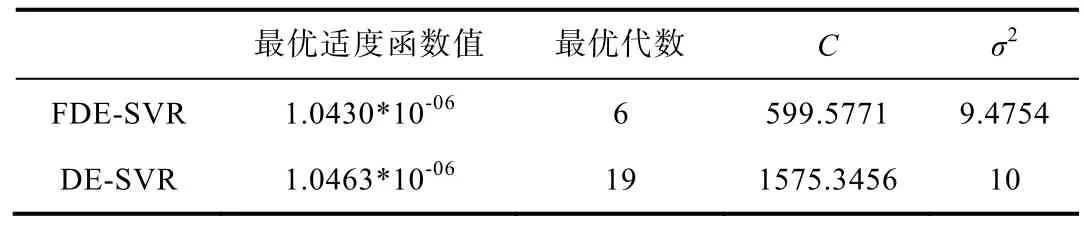
表4　SVR结果对比

由表（4）得出来的最优参数可以得到以下对应的辨识模型图：

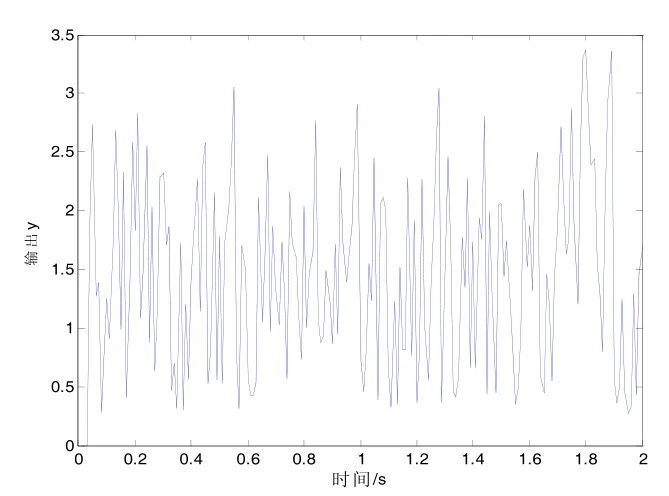
图5　FDE-SVR辨识模型输出

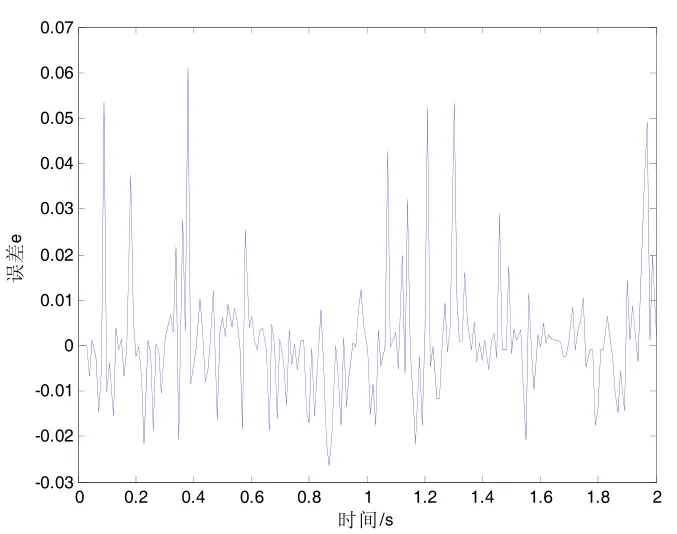
图6　FDE-SVR辨识模型输出

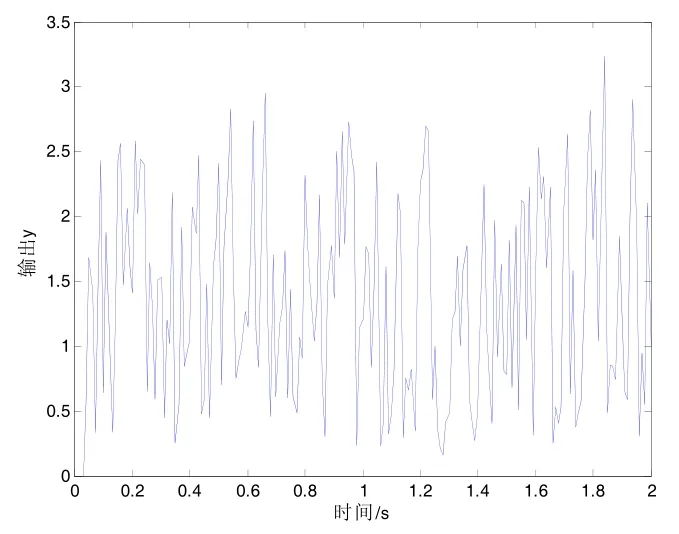
图7　DE-SVR辨识模型输出

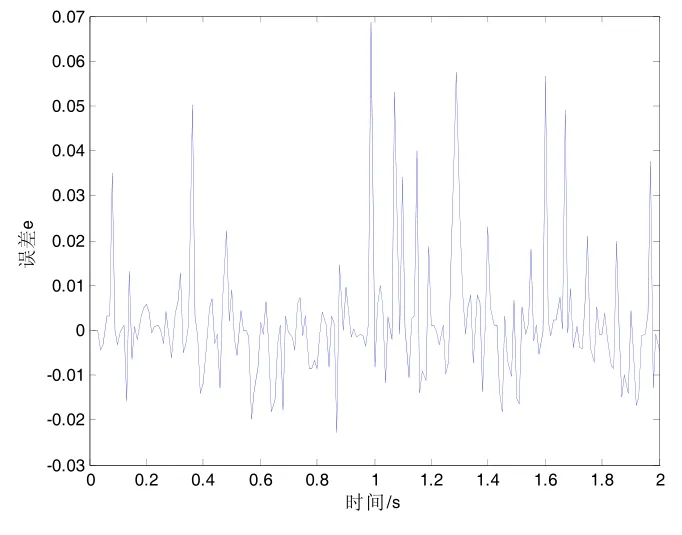
图8　DE-SVR输出误差

图（5）FDE-SVR辨识模型输出和图（6）DE-SVR输出误差，图（7）FDE-SVR输出误差和图（8）DE-SVR辨识模型输出可以得出结论：SVR在对模型进行辨识时，得出了模型误差精度都达到 10-2。差别可以在图1和图2中看出来，仅仅是在得到最优参数时需要进化的次数。

2.5模型验证

为了验证辨识出的模型的性能，采用的校验信号分别为：幅值为1的阶跃信号。

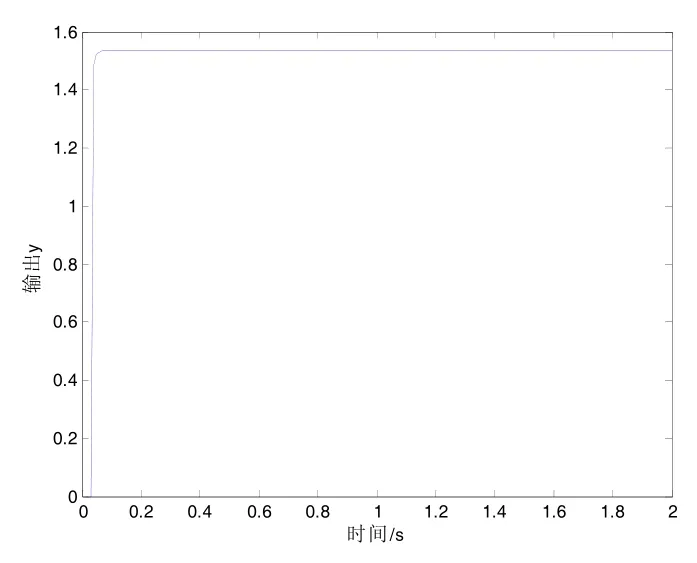
图9　阶跃信号FDE-SVR辨识建模输出

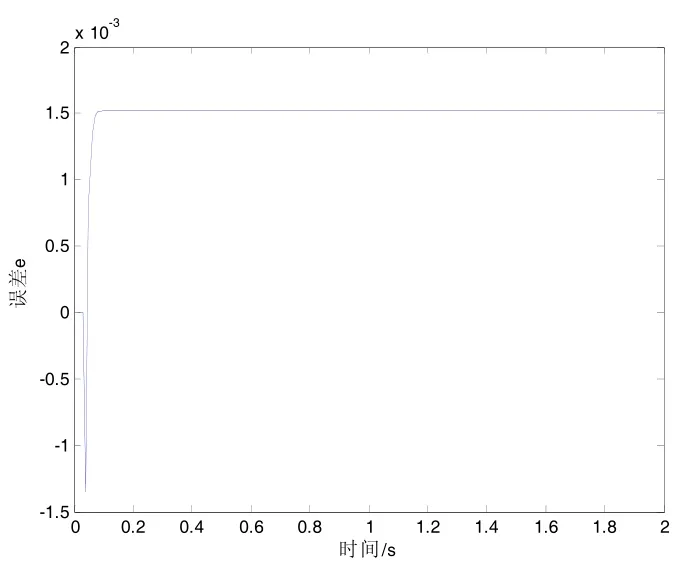
图10　阶跃信号FDE-SVR辨识校验误差

由图9阶跃信号FDE-SVR模型辨识输出和图10阶跃信号FDE-SVR辨识校验误差可以知道，辨识误差为 10-3数量级，说明使用FDE-SVR得到的模型具有良好的泛化能力。

3　结论

论文针对非线性系统辨识中系统模型难以确定的问题，提出基于 FDE-SVR的非线性系统辨识方法，使用FDE-SVR模拟非线性系统模型。FDE-SVR可以避免SVR参数反复试凑的过程，快速高效的获取SVR的相关参数。使用FDE-SVR辨识出的非线性系统模型具有较高的精度。最后，论文使用阶跃信号验证了FDE-SVR辨识出模型的有效性。

（责任编辑 杨文忠）

［1］ 王鲜芳，王岁花，杜昊泽，王平.基于模糊粗糙集和支持向量机的化工过程故障诊断［J］.控制与决策，2015（2）：353-356.

［2］ 王鲜芳，王平，张帅，李贺.基于 SVM和 MCGS的生化过程故障诊断设计［J］.郑州师范教育，2015（6）：35-38.

［3］ 王文栋，郭伟.基于SVR的控制系统辨识建模研究［J］.燃气涡轮试验与研究，2009（3）：33-36.

［4］ 吴德会.非线性动态系统的SVR辨识法［A］. 中国自动化学会控制理 论专 业委 员会（Technical Committee on Control Theory，Chinese Association of Automation）.第二十六届中国控制会议论文集［C］.中国自动化学会控制理论专业委员会（TechnicalCommitteeonControlTheory，Chinese Association of Automation）：，2007：4.Zadeh L.A. From circuit theory to system theory［J］. Proceedings of the IRE.1962，50（5）：856-865.

［5］ CorinnaCortes，VladimirVapnik.Support-Vector Networks［J］.1995，Machine Learning（3）：273-297.

［6］ B. E. Boser， I. M. Guyon， V. N. Vapnik. A training algorithm for optimal margin classifiers. In Proceedings of the 5th annual ACM Workshop on computation learning theory［M］.ACM Press.1992，144-152.

［7］ 闫雨石.几类特殊模糊集的理论与应用探析［J］.数字技术与应用，2015（3）：202.

［8］ 盛明明，黄海燕，赵玉.基于克隆选择的误分进化算法及其在SVM中的应用［J］.计算机科学，2015（S2）：19-21，48.

TP183

A

1008-2093（2016）03-0006-05