一道高考解三角形试题的多解与感悟

北京市第十二中学　(100071)

刘　刚　赵　毅



一道高考解三角形试题的多解与感悟

北京市第十二中学(100071)

刘刚赵毅

三角内容在高中数学中占有重要的地位，是高考的重点．三角中的许多问题，如求值、恒等式(不等式)的证明等，不仅能用代数法解决，还可以找到它的几何模型，利用几何法解决．这不仅可以使学生体会数形结合这一重要的数学思想，深刻认识三角问题的本质；还可以培养学生综合运用数学知识来解决问题的能力，提高解题的灵活性．下面以一道高考求角试题为例，进行解法剖析与变式梳理，以此丰富我们的教学思路．

1.试题

例1(2015湖南，文17)设ΔABC的内角A,B,C的对边分别为a,b,c,a=btanA.

(Ⅰ)证明：sinB=cosA；

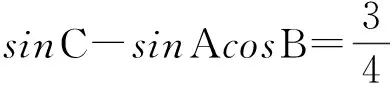
2.试题特点

本题是一道解三角形问题，主要考查正(余)弦定理、和差角公式、二倍角公式、诱导公式等知识以及三角恒等变换中的数学思想方法，检验学生的推理与计算能力．已知条件中边、角同时存在，通常这类问题有两种解法：边化角或角化边，使得边角进行统一，本题边化角较容易转化，从而证明(Ⅰ)问．(Ⅱ)问既可以通过三角恒等变换用代数法解决，也可以构造图形用几何法解决，考查学生的创新能力．

3.解法分析

(Ⅰ)略，(Ⅱ)解法如下：

思路一、代数法

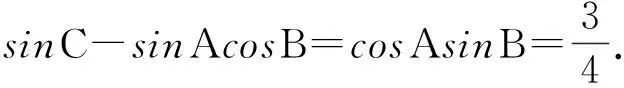
点评:由于A,B,C在已知等式中都有，且它们的和为π，因此可以消元进行求解．消掉哪一个角呢？如果消A或B，那么sinAcosB在展开后就变为3次，那后面就更难求解了，因此可以消掉C，也就是sinC可以用sin(A+B)表示， 在展开后可以与sinAcosB进行合并，这样问题就可以得到解决，所以要结合代数式的特点进行消元．

点评:解法2还是进行消元处理，结合已知条件得到有两个角可以用剩下的一个角表示，这样就得到了关于这个角的方程，然后再利用诱导公式、二倍角公式进行求解．

点评:解法3从等式结构特点出发，先利用积化和差公式变为一次的形式，通过合并再利用和差化积公式进行消元，变换技巧强，对学生的计算、推理能力是一种考验．

思路二、几何法

图1

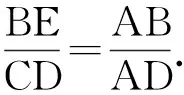
点评:解法4通过构造直角三角形，把涉及到的三角函数都用边来表示，然后找出边的关系，从而使问题得以解决．

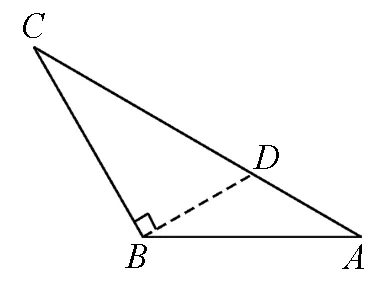
图2

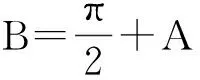
点评:解法5充分利用角A,B之间的关系，过点B构造出一个直角，则剩下的角与A相等，由此分析图形特点进而得出答案．

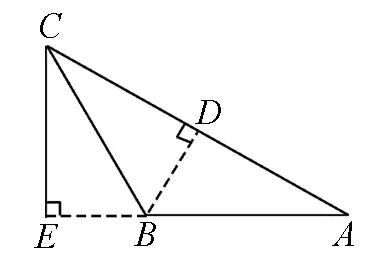
图3

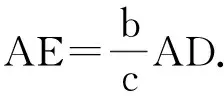
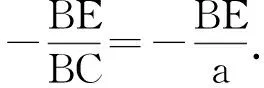
点评:解法6通过化斜为直，分析图形特点，把三角函数都用边来表示，找出内在关系，又进一步得到了函数值之间的关系，体现了数形结合的思想方法．

图4

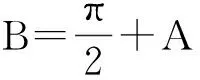
点评:解法通过作垂直、平行线等添加辅助线方法，利用图形特征，借助三角形相似、勾股定理等平面几何知识使问题得以解决，综合性强．

本题(Ⅱ)问通过代数法和几何法使问题得以解决．代数法就是运用定义、公式、定理等知识进行代数运算，从而求得答案，具有模式化、套路化、对计算能力要求高等特点．几何法就是适当添加辅助线构造基本图形，利用图形特点，运用平面几何知识进行解答，计算量通常较小．本题(Ⅱ)问在运用几何法的过程中，通过化斜为直解题，令人耳目一新，回味无穷，强化了学生数形结合的解题思想．

4　变式梳理

在高考解三角试题中，很多题目都可以化斜为直运用几何法进行解决，不仅可以避免三角变换中解题技巧，还可以减少计算量，往往能取得较好的效果，下面再举几例进行说明．

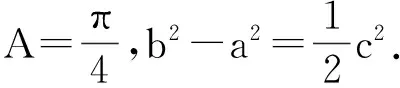
(Ⅰ)求tanC的值；

(Ⅱ)若ΔABC的面积为3，求b的值．

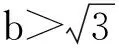
图5

点评:在作高时注意判断要作哪一条边上的高，本题求角C的函数值，另外角A已知，因此过点B作三角形的高比较容易解决问题．另外还要注意判断作垂线时垂足的位置．

图6

点评:本题如果直接考虑代数法，计算量会很大，很多学生解不对或求不出．但如果是结合已知条件作一条高效果就大不一样了，因此在解题时一定要注意分析图形特点，适当添加辅助线，然后再代数计算，这是一种常用的思维方式．

例4(2015全国Ⅰ，理16)在平面四边形ABCD中，∠A=∠B=∠C=75°，BC=2，则AB的取值范围是.

解析:如图7，延长BA，CD交于点E，平移AD，

图7

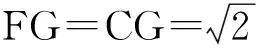
点评:在解题过程中要注意分析角之间的关系，由此构造了含45°角的直角三角形，使得问题的解决大大得到了简化．

5　解题感悟

本文介绍了代数法、几何法在解三角形试题中的应用．实际上，相当多的题目并没有明显的几何特征，用几何方法是比较困难的，往往要用代数法进行解决．在解题过程中这两种方法并不是独立的，通常先用几何法挖掘图形特点，适当添加辅助线，然后再用代数法进行解决，这就是通性通法．教师要注意这方面的引导，这样才能取得较好的解题效果，才能揭示问题的本质，从而提升解题的针对性．