一道调研题的多解对二轮复习的启示

江苏省泰州市姜堰区蒋垛中学　(225503)

臧　华



一道调研题的多解对二轮复习的启示

江苏省泰州市姜堰区蒋垛中学(225503)

臧华

通过高考一轮复习，学生的数学基础知识和解题方法学了那么多，但是一遇到能力题还是用不上，究其原因在于一轮复习的知识过于零碎，未成体系；单个方法像珍珠一样没有用题目连成串．笔者攫取了一道双变量求最值的调研题，通过对解题方法的剖析谈一谈二轮复习的启示.

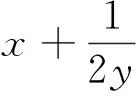
考情分析：多元变量问题求最值是高考的重点题型，且花样不少、难度颇大，许多学生常出现问题．

方法准备：减元法、换元法、构造法、基本不等式等.

在波利亚的四个解题步骤中，审题最重要，而审题有这样一个技巧：当你对整道题目没有思路时，可以将题目条件推导出“新条件”，将结论推导到“新结论”.

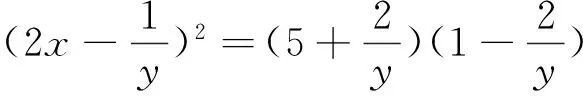
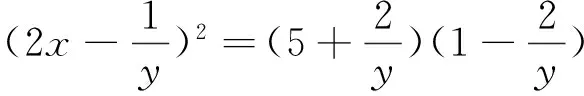
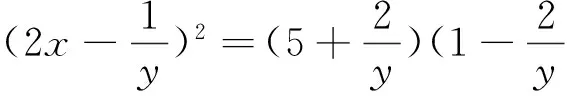
评注：将条件和结论整体代换后，问题就变成了我们熟悉的直线与圆的位置关系.

评注：只要看到圆和椭圆的结构式，我们都可以尝试用三角换元处理双变量问题，然后利用三角函数的有界性求最值.

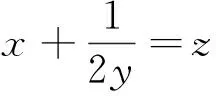
评注：因为正实数x,y满足方程(2xy-1)2=(5y+2)(y-2)，因此可以利用方程有解的思想来处理.

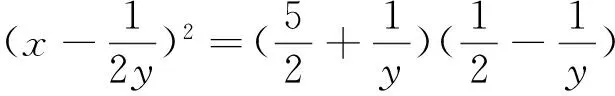
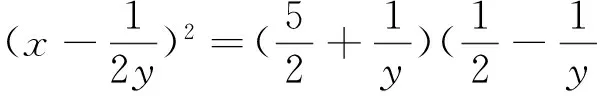
感悟双变量问题求最值一般有三个方向可考虑：一是消元法,即利用已知方程，消去一个未知数，得到单变量的函数形式；二是构造法(构造同元、同次、同结构)，把条件和结论中的不同结构的未知数通过构造转化成相同的元素；三是换元法(整体换元、三角换元)化生题为熟题，一道难题，难就难在题目条件与结论的关系难以建立，而你自己推出的“新条件”与“新结论”之间的关系往往比原题更容易建立，这也意味着解出题目的可能性也就越大．

启示一轮复习结束之后，学生已经掌握了很多知识和方法，也有了一定的解题基础，但是碰到能力题还是一筹莫展，如今高考对能力题提出由“知识立意”向“能力立意”的转变要求，这就要求二轮复习不能原地踏步，而要重视构建知识体系，将解题方法“散珠成串”，搭建思考问题的“脚手架”，在问题解决中体验知识、方法、思想的用途，重视一题多解，达到用数学的眼光去观察问题，自动化地联想与转化，寻求最佳求解方案；二轮复习要坚持在问题解决中潜移默化强化策略性知识的培养，不断渗透程序性知识，提升利用概念解题的自动化水平，帮助学生构建相互联系的知识结构．