基于启发式采样算法的二自由度机械臂轨迹规划

阮玲燕，余晓流，杨　帆，鲁嗣昂，史威严（安徽工业大学机械工程学院，安徽马鞍山243032）

基于启发式采样算法的二自由度机械臂轨迹规划

阮玲燕，余晓流，杨帆，鲁嗣昂，史威严
（安徽工业大学机械工程学院，安徽马鞍山243032）

针对传统的采样类轨迹规划算法存在随机性、计算效率低等问题，根据机械臂运动学约束，给出关于关节空间的启发式采样轨迹规划算法。采用拉格朗日法建立二自由度机械臂的动力学模型，以角加速度为采样对象，通过积分器采集角速度与角度位移进行转矩的实时检测，结合启发式采样算法，实现给定目标位姿的轨迹自动规划；且对机械臂两关节在不同负载下的运动位置、速度在MATLAB中进行仿真，并与传统的B-spline轨迹规划方法比较。结果表明，启发式采样算法可实现不同负载下给定目标位姿路径的自动规划，且在时效性及路径规划上具有优越性。

启发式采样算法；二自由度机械臂；拉格朗日法；轨迹规划

轨迹规划优化是近年来机械臂研究的主要方向，传统的轨迹规划主要分4个步骤［1-2］：计算1条无碰撞轨迹；考虑约束状况，平滑可实现路径；参数化平滑路径，获得机器运动轨迹；设计反馈控制器，跟踪轨迹。传统轨迹规划方法中，上一步中出现的问题会直接影响下一步轨迹规划，且效率不高［3-5］。

为解决上述弊端，多数学者采用采样类轨迹规划方法，其搜索特性大幅提高了计算效率。其中Ripidlyexploring Random Tree（RRT）［6］算法是重要的采样类算法之一，主要应用于机器人轨迹规划，其高效的搜索特性使其可直接应用于非完整性约束或非完整性动力学约束规划中，但随机采样生成的扩展树，二次规划路径的非重复性及随机性直接影响轨迹规划结果，存在较大轨迹偏差。代彦辉等［7］针对RRT算法中新生成随机点远离目标节点的问题，以基准向量为基准选择节点扩展方向，逐渐增加子节点，降低了节点生成的随机性并提高了扩展速度，但并未利用RRT算法搜索的高效性来优化轨迹。近年来，A*算法在路径优化领域中得到了广泛应用［8-10］，其利用启发函数估计任意点到目标点的远近程度，减少了搜索面积，但搜索效率与启发函数有关，多参数的启发函数会影响轨迹规划的计算效率及解的精确性。

借鉴上述算法的优点，文中基于RRT树状结构的随机采样与A*算法的启发式搜索思想，以二自由度机械臂为研究对象，给出一种启发式采样轨迹规划算法。

1　二自由度机械臂的动力学模型

二自由度机械臂连杆结构如图1所示。图中：l1，l2分别为连杆1，2的长度；q1为杆1与y轴间的夹角；q2为相邻两杆之间的夹角；d1为杆1质心与关节O处的距离；d2为杆2质心与关节A点处的距离。

图1　二自由度机械臂结构Fig.1 Structure of 2 DOF manipulator

建立如图1所示的坐标系，坐标原点O（0，0）与第一个关节重合，末端执行器的位置用（xB，yB）表示。末端执行器的位置坐标由连杆长度和关节角度关系确定，可表示为：

末端执行器的速度方程可表示为：

其中q̇1，q̇2分别为杆1与杆2的角速度。质点系的拉格朗日方程可表示为

式中：L为拉格朗日函数；K为系统动能之和；P系统势能之和，则动力学方程可表示为

式中：τi表示杆i的转矩；q̇1表示杆i角速度；qi表示杆i角度位移。设机械臂连杆的质量m1集中在杆1的C处；m2集中在杆2的D处；I1为杆1对关节O点处的转动惯量；I2为杆2对关节A点处的转动惯量。计算杆1，2的动能Ki和势能Pi（i=1,2）。对于杆1的动能和势能分别为：

同理，杆2的动能和势能分别为：

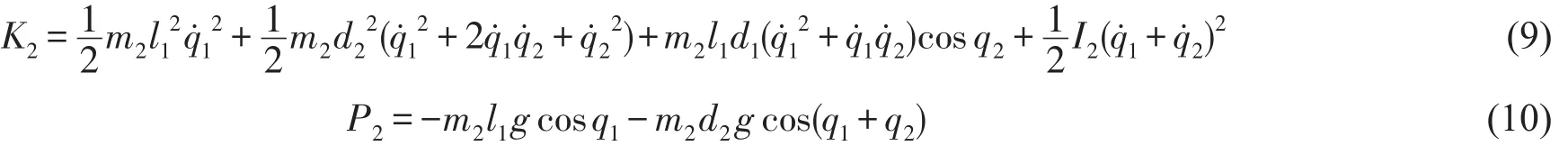
最终可得

将式（11）代入式（6）可分别求出相应关节处的转矩τ1和τ2。

2　启发式采样算法

启发式采样算法包括采样与启发评估两部分，采样主要通过Halton序列［11］生成采样序列，通过启发评估控制随机节点向目标节点的收敛方向，上一节点与当前节点及当前节点与目标节点间的欧几里得距离之和G的最小值Gmin为节点保存准则。其算法流程如图2，初始节点表示为nin，当前节点表示为nc，目标节点表示为ngo，m为用户可设定的子节点数目，栈CLOSE可连续推入有效节点，a为栈CLOSE中有效节点数目。

本文以给定目标位姿的二自由度机械臂为例，采用启发式采样算法进行轨迹规划，以最短路径为基本原则控制节点生成的方向，并以角加速度q̈替代图（2）中的节点作为采样对象，通过2个积分器分别获得机械臂的角速度q̇和角度位移q，避免对系统的动力学模型直接积分，运动学模型如图3。其中角度位移q与角速度q̇分别为对角加速度q̈的二次与一次积分，角加速度q̈（t）在采样时间间隔T内默认为常数，q̈（t）=q̈（mT）,t∈［mT,mT+T］，m为自然数。

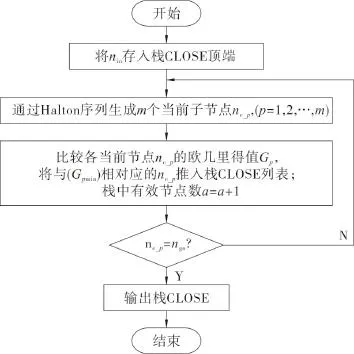
图2　启发式采样算法的流程图Fig.2 Flow Chart of heuristic sampling algorithm

图3　二自由度机械臂的运动学模型Fig.3 Kinematic model of 2 DOF manipulator

基于启发式采样算法下的二自由度机械臂轨迹规划步骤如下。

1）初始化并建立可保存有效节点的栈CLOSE。以q̈为采样对象的采样节点n，分别得到q̇和q以及转矩τ，即节点n组成得6维向量，j为初始节点与目标节点的总节点数。

2）逐点比较。在每个当前节点nc处产生m个子节点，分别比较上一节点与当前节点及当前节点与目标节点间的欧几里得距离之和G，并将Gmin相对应的当前节点推入栈CLOSE中。其中，排除超过转矩和角速度范围的节点。

3）迭代重复步骤2），直到接近或者达到目标节点。

4）保存。得到从初始位姿到目标位姿的所有优化节点，即二自由度机械臂两关节的角度、角速度以及关节处的转矩。

3　仿真结果与分析

3.1二自由度机械臂启发式采样算法仿真结果与分析

在MATLAB中对二自由度机械臂在启发式采样算法下进行轨迹仿真，算法参数与机械臂参数如下：

1）启发式采样算法的参数选择。随机产生角加速度q̈采样点上限总数为13 000，单个节点可产生4个分支，即m=4，时间间隔T=0.02；

2）机械臂参数。以含2个旋转关节的机械臂为研究对象，几何参数如表1，各关节的角度、角速度以及角加速度约束如表2。

基于以上参数限制条件，选定最终目标位姿（553.0 mm，-236.0 mm），对机械臂末端执行器分别持负载0，1.0，2.5 kg的运动轨迹进行仿真，结果如图4，5。

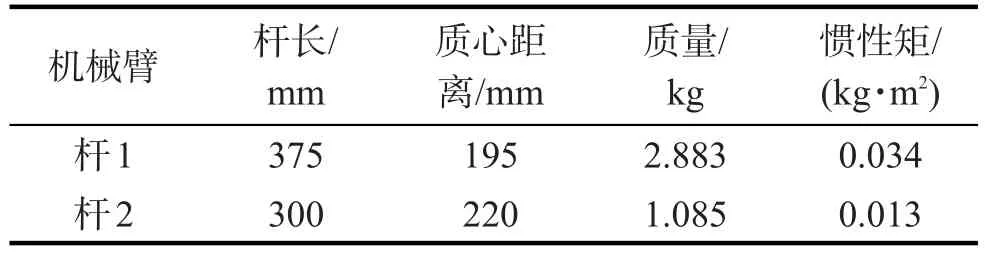
表1　机械臂的基本参数Tab.1 Basic parameters of manipulator

表2　机械臂运动约束参数Tab.2 Parameters of Motion Constraints of Manipulator

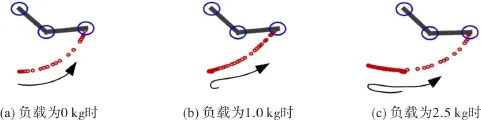
图4　二自由度机械臂在不同负载下的运动轨迹Fig.4 Trajectory of 2 DOF manipulator under different loads

图5　二自由度机械臂不同负载下各参数变化曲线Fig.5 Variation of parameters of 2 DOF manipulator under different loads

从图4可以得出：当负载为0 kg时，机械臂无回摆运动；负载为1.0 kg时，机械臂出现小幅度摆动；负载为2.5 kg时，机械臂相对于负载1.0 kg时有较大摆动，反映了在考虑转矩等动力学约束条件下，启发式采样算法从初始位姿到达目标位姿轨迹规划的自适应性。

图5为不同负载下（0，1.0，2.5 kg）关节1，2的角度位移、角速度、转矩的变化曲线。由图5（a），（b）可知，不同负载下，关节1，2最终角度位移分别为0.75，0.95 rad；由图5（c），（d）可知，关节1，2的角速度均为0 rad/s。由此可见：启发式采样算法可实现给定目标位姿下二自由度机械臂的轨迹规划；不同负载下机械臂到达给定目标位姿分别需21，26，52步，且机械臂在负载1.0，2.5 kg下，关节1角度位移与角速度相对于负载0 kg出现负值（即反向摆动），体现了启发式采样算法对于考虑转矩问题轨迹规划的自适应性。从图5（e），（f）可见，不同负载下，关节1相较于关节2转矩变化明显，表明启发式采样算法对关节1处的冲击较关节2处大，但仍在要求的-10～10 N·m范围内，且负载越小，对关节处的影响越小。

不同负载下目标位姿的模拟结果与实际位置的比较结果见表3。由表3可知：负载越轻，计算步数越少，轨迹规划时间越短，精确度越高；启发式采样算法在目标位姿的定位上存在一定的偏差，偏差大小与负载无关。

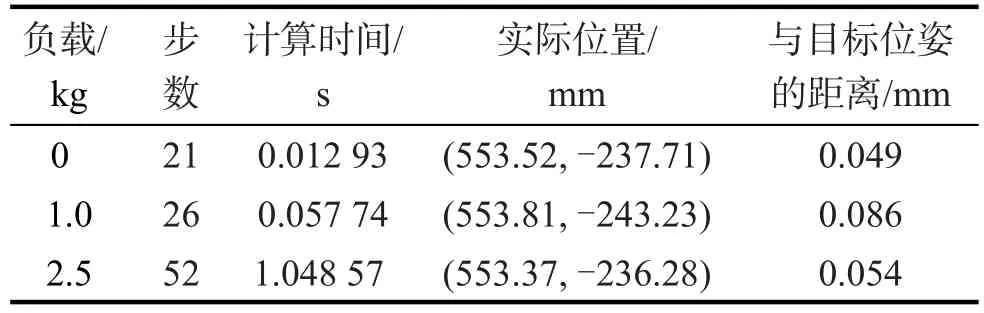
表3　不同负载下目标位姿的比较Tab.3 Comparisonoftargetpositionbetweendifferentloads

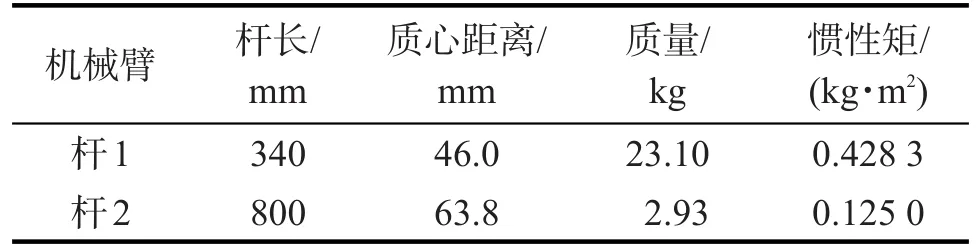
表4　机械臂的基本参数Tab.4 Basic Parameters of manipulator

图6　　不同算法下2个关节运动数据Fig.6 Data of two joints using different algorithms

综上分析可看出，启发式采样算法可以实现不同负载下的自动轨迹规划。通过积分器获得2关节角速度、角度位移，避免了对动力学模型直接积分及算法中出现多参数变量而导致计算速率降低。同时，关节1，2处在不同负载下的角度位移、角速度及转矩曲线体现了启发式采样算法的自适应性，为后续的研究奠定了基础。

3.2启发式采样算法与传统算法仿真结果对比分析

徐春泉等［12］采用B-spline传统算法实现二自由度机械臂轨迹规划，本文根据文献［12］中机械臂基本参数（表4），且采用启发式采样算法实现二自由度机械臂轨迹规划，所得对比结果如图6。从图6可以看出：到达指定目标位姿（395.62 mm，-187.83 mm）处，启发式采样算法得到的运动轨迹较B-spline算法平缓，规划时间短；同等条件下，启发式采样算法规划耗时0.82 s，B-spline算法规划耗时1.23 s。由此可见，启发式采样算法在二自由度机械臂的轨迹规划较B-spline方法在轨迹优化上具时效性及优越性。

4　结　论

结合采样与启发评估进行机械臂的轨迹规划，给出一种启发式采样优化的轨迹规划算法，将电机转矩的限制并入启发评估中，实现最短路径规划和实时优化。同时，对机械臂在不同负载下的运动轨迹进行仿真。仿真结果显示，启发式采样算法可实现在相关约束下二自由度机械臂自动搜索的轨迹规划，机械臂末端执行器可到达目标位姿，实现了二自由度机械臂在不同负载下对于给定目标位姿的路径自动规划。相较于B-spline轨迹规化方法，启发式采样算法具有规划时间短，路径平滑的优势。未来的研究重点是结合启发式采样算法模拟实现二自由度机械臂的目标位姿投掷过程，并对启发式采样算法进行进一步优化。

［1］LAVALLE S.Robotics andAutomation Magazine［M］.Boca Raton：CRC Press，2011：108-118.

［2］熊少康，章家岩.一种基于细菌觅食算法的机械手臂控制器设计［J］.安徽工业大学学报（自然学科版），2014，31（3）：290-294.

［3］DUNLAP D，COLLINS E G，YU W.Motion planning for steep hill climbing［C］//IEEE International Conference on Robotics and Automation.Shanghai：ICRA，2011：707-714.

［4］KARAMAN S，FRAZZOLI E.Optimal kinodynamic motion planning using incremental sampling-based method［C］//IEEE Conference on Decision and Control.Atlanta，Georgia：CDC，2010：7681-7687.

［5］PLAKU E，KAVRAKI L E，VARDI M Y.Motion planning with dynamic by synergistic combination of layers of planning［J］. IEEE Transaction on Robotics，2010，26（3）：469-482.

［6］LAVALLE S M，KUFFNER J J.Randomized kinodynamic planning［J］.International Journal of Robotics Research，2001，20（5）：378-400.

［7］代彦辉，梁艳阳，谢刚.基于RRT搜索算法的六自由度机械臂避障路径规划［J］.自动化技术与应用，2012（10）：31-37.

［8］DUNLAP D D，CALDWELL C V，COLLIONS E G.Motion Planning for Mobile Robots Via Sampling-based Model Predictive Optimization［M］.INTECH OpenAccess Publisher，2011：24-112.

［9］DIANKOV R，KUFFNER J.Randomized statistical path planning［C］//Proceedings of IEEE International Conference on Intelligent Robots and Systems.Boca Raton：CRC Press，2007：1-6.

［10］KOENIG S，LIKHACHEV M，FURCY D.Lifelong planningA*［J］.Artificial Intelligence，2004，155（1）：93-146.

［11］LAVALLE S M.PlanningAlgorithms［M］.Cambridge：Cambridge University Press，2006.

［12］XU C Q，MING A.Optimal Trajectory Generation for Manipulator with Strong Nonlinear Constraints and Multiple Boundary Conditions［C］//Proceedings of IEEE International Conference on Robotics and Biomimetics.［s.l.］：ROBIO，2004：192-197.

责任编辑：何莉

Path Planning for 2 DOF Manipulator Based on Heuristic Sampling Algorithm

RUAN Lingyan，YU Xiaoliu，YANG Fan，LU Si'ang，SHI Weiyan
（School of Mechanical Engineering，Anhui University of Technology，Ma'anshan 243032，China）

Due to the problems of randomness and low computational efficiency of the traditional sampling algorithm，a heuristic sampling algorithm，taking the kinematic constraints of the arms into consideration，was proposed.The automatic path planning using heuristic sampling algorithm was achieved by establishing the Lagrangian dynamic model of 2 degree of freedom（2 DOF）manipulator，and the joint angle and angular velocity which implemented the real-time detection of joint torque，was obtained by using the integrator in sampling angular acceleration.The trajectorys of angle and angular velocity of the two joints under different loads were simulated with MATLAB and compared with that of B-spline method.The result of the simulation verifies that the trajectory can be planned automatically under different loads by using heuristic sampling algorithm，which has advantages in timeliness and path planning.

heuristic sampling algorithm；2 degree of freedom manipulator；Lagrangian method；path planning

TP242

Adoi：10.3969/j.issn.1671-7872.2016.02.008

1671-7872（2016）02-0130-05

2015-10-21

国家自然科学基金项目（50905122，5375013）；安徽省自然科学基金项目（1208085ME64）

阮玲燕（1990-），女，安徽马鞍山人，硕士生，主要研究方向为机器人设计与控制。

余晓流（1962-），男，安徽安庆人，博士，教授，主要研究方向为机器人及其检测技术，先进制造技术方向。