量纲分析理论在气淬钢渣粒化度问题中的运用

魏环，常锦才，薄惠丰

(华北理工大学 理学院，河北 唐山 063009)



量纲分析理论在气淬钢渣粒化度问题中的运用

魏环，常锦才，薄惠丰

(华北理工大学 理学院，河北 唐山 063009)

气淬粒化；粒化度；量纲分析；Π定理；物理相似性原理；相似准数

气淬粒化钢渣工艺是目前正在研究与探索的干法处理钢渣的一种新工艺，确保钢渣气淬后具有一定的粒化度是这一工艺要达到的目标之一。该项研究围绕气淬钢渣的粒化度问题，运用量纲分析理论，分析了钢渣的粒化度与各种控制参量的关系，并为获得这一关系及气淬工艺的最佳控制参数提出了模拟实验方案。

钢渣是转炉炼钢过程中由铁水中的各种元素(如Fe、Ca、Mg、Si、Mn、Al、P等)氧化形成的氧化物与造渣剂以及熔蚀的耐火材料等多种成分结合而成的炉渣。钢渣出炉时的温度约在1 450～1 650℃范围内，是介于理想固体和液体之间的典型高温黏弹性物质。气淬粒化钢渣工艺是目前正在研究与探索的干法处理这种“液态”钢渣的新工艺，它是利用高压氮气通过气流喷嘴产生的高速射流所携带的巨大动能，使液态钢渣粒化和放热的。与风淬钢渣处理法相比，氮气气淬钢渣处理工艺，可以为实现液态钢渣的显热、单质铁和尾渣矿物等三大资源的高效回收利用奠定更为有利的基础[1-6]。

由于钢渣的化学成分与水泥相似，其尾渣矿物通常作为制造水泥的原料，所以使钢渣气淬后具有一定的粒化细度(譬如渣粒的特征长度应小于3 mm，达到中沙大小)以节省细磨尾渣的费用，是气淬工艺使尾渣矿物能够高效回收利的一个重要目标。

钢渣的气淬粒化过程极其复杂，目前尚未建立起精确的数学模型来描述和解释其气淬现象。量纲分析法在处理没有现成的数学模型及方程的一类复杂问题时，具有独特优势与作用。该方法是在量纲一致的原则基础上，对物理量之间的关系进行分析，从基本物理观点出发来剖析问题，通过判断问题的性质及其控制参数来设计模拟实验，在反复的模拟实验过程中，寻找和整理出主要物理量之间的定量关系式，再去指导实践，达到最终解决实际问题的目的[7]。

该项研究运用量纲分析理论对影响气淬钢渣粒化度的因素进行分析研究，探寻其中的因果规律，并为获得气淬粒化钢渣的最佳控制参数提供模拟实验方案。

1量纲分析理论

1.1Π定理

量纲分析法的理论基础是Π定理，该定理是E.Buckingham在1914年提出来的，定理内容可表述如下[7，8]：

设某个问题涉及n+1个物理量p,p1,p2,…,pn，它们之间的函数关系式为

p=f(p1,p2,…,pn) ，

(1)

如果在选用的单位制中共涉及k个基本量纲，则在上述物理量中必存在k个线性无关的物理量，这k个独立的物理量可以作为一组基矢去度量其余的物理量，并且可以形成n+1-k个无量纲的量Π定理i(i=1,2,…,n+1-k.)。

若取p1,p2,…,pk作为一组基矢，则可以将式(1)表达成无量纲形式

Π=F(Π1,Π2,…,Πn-k).

(2)

其中，Π是对应于p的无量纲量，Π1,Π2,…,Πn-k则是分别对应于pk+1,pk+2,…,pn的无量纲量，每一个无量纲量均可表示为：

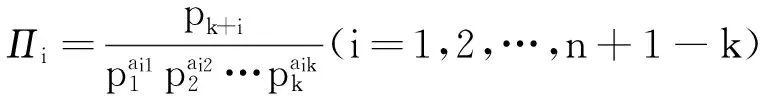
(3)

其中，ai1,ai2,…,aik为一组待定的幂指数。

无量纲量又称无量纲特征数，这些特征数反映了各个物理量之间相互影响与相互制约的关系，因此式(2)是更能揭示现象本质的无量纲因果关系式。

1.2物理相似性原理

式(2)给出了现象的因果规律，但是函数F的具体形式一般不能单纯依靠Π定理来获得，而是需要依靠实验或理论来求得。在工程技术以及其它领域中，有许多物理模型和数学方程还不清楚，还不能从基本原理出发获得解决的复杂问题，此时往往采用模拟实验的手段来解决问题。模拟实验是指人们用模型代替实际的原型而进行的研究实验，进行模拟实验的目的是为了指导实践，而能够将模拟实验的结果拿来指导实践的前提条件是，模拟实验(模型)与实际现象(原型)之间必须满足物理相似性原理[9-12]。

物理相似性原理指出：如果2种(或1组)物理现象相似，则2种(或1组)现象中的同名无量纲特征数必然相等，即：

(Πi)原型=(Πi)模型。

(4)

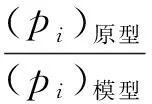
可见，量纲分析法作为一种定性分析的方法，并不单独使用，它需要与物理相似性原理相结合来完成对相应问题的研究。

2液态钢渣破碎过程的量纲分析

2.1影响钢渣气淬粒化度的主要因素

液态钢渣粒化的目标之一是利用氮气气流将钢渣破碎成符合生产计划要求的细小颗粒(注：用φ来量化表示破碎渣粒的特征长度，并称φ为钢渣的粒化度)，将气淬工艺中钢渣粒化度与相关的控制参量之间的关系以及气淬工艺的最佳控制参数作为关注和研究的重点。由于钢渣破碎过程极其复杂，破碎过程中液渣形状变化的所有状态无法详尽描述，因此，基于本文关注的重点，认为可以忽略破碎过程中液渣形状变化的细节，将破碎过程简化为液态钢渣在高压氮气射流冲击作用下被击碎成细小颗粒的动力学过程。

影响钢渣粒化度φ的主要因素包括氮气与液态钢渣两方面的控制参量。从物理角度看，钢渣气淬过程是两相流体之间的相互作用过程，也是动能与动量传输的动力学过程。气淬钢渣不仅需要高压氮气射流提供巨大的破碎动能，同时还需要氮气提供足够强大的冲击动力。从基本物理原理出发分析可知，气体的压强pg与气流喷嘴口径D决定了气流的冲击力，而单位时间内气流提供的动能大小则由气体压强pg、流速vg和气流喷嘴口径D三者共同决定；高温粘弹性液态钢渣是在氮气射流形成的冲击力以及自身的粘滞力和表面张力的共同作用下被破碎粒化的，因此，其粒化度与液态钢渣自身的密度ρl、粘度系数μl及表面张力系数σl有关。另外，转炉产生的钢渣流量Ql是不稳定的，氮气应该提供多大的动能还与钢渣流量有关，即钢渣的流量是对氮气射流的控制参数构成影响与限制的重要因素。

基于上述分析，钢渣破碎过程的主要控制参量分别是：

(1)氮气的控制参量为气流喷嘴出射的气体压强pg和出射的气流流速vg；

(2)气流喷嘴口径的特征长度为D；

(3)钢渣的控制参量为钢渣流量Ql；

(4)钢渣的本构参为密度ρl、粘度系数μl和表面张力系数σl。

2.2对气淬过程的量纲分析

在本问题中，将气淬钢渣粒化度φ作为因变量，设它与上述7个控制参量(作为自变量)存在函数关系：

φ=f(pg,vg,D,ρl,μl,σl,Ql)

(5)

本问题涉及的独立量纲为长度L、质量M和时间T，在式(5)中，物理量的总数为n+1=8，这8个物理量的量纲分别为：

[Pg]=ML-1T-2，[vg]=LT-1，[D]=L，[φ]=L；

[ρl]=ML-3，[μl]=ML-1T-1，[σl]=MT-2，[Ql]=L3T-1。

根据Π定理，上面8个物理量中存在着3个具有独立量纲的基本物理量，同时应该形成n+1-k=5个独立的无量纲特征数或相似准数(注：此后称无量纲特征数Π为相似准数)。

现取D、vg、ρl3个量作为基本物理量，它们的量纲表如下：

DvgρlM001L11-3T0-10

设5个相似准数的表达式为

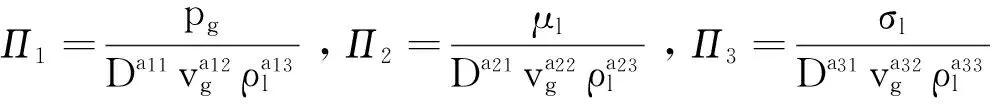
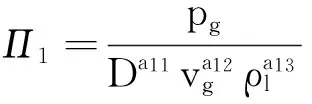
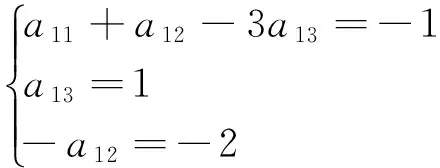
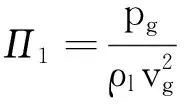
(6)

同理可得：

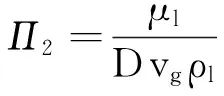
(7)

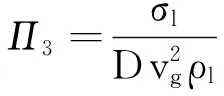
(8)

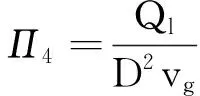
(9)

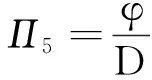
(10)

Π5=F(Π1,Π2,Π3,Π4)，

(11-a)

(11-b)

3关于模拟实验方案

如前所述，式(11)中函数的具体形式，不能仅凭Π定理获得，需要进一步结合物理相似性原理，通过模拟实验的方法来获得。事实上，由于钢渣出炉时的温度约在1 500 ℃左右，若直接对液态钢渣进行气淬粒化的实验研究，就必然需要处理与高温有关的诸多实验难题，所以，通过选择符合相似性原理要求的液态钢渣模型、借助模拟实验间接获得对气淬粒化原过程的经验性认识，无论从经济角度还是可操作角度考虑都是必然的选择。

3.1建立具有经验性质的钢渣粒化度与其控制参量间的因果关系式

在设计气淬粒化的模拟实验时，需要将每个相似准数作为区别不同状况的自变量，同时将式(11)构造成如下幂次形式：

(12)

其中，C为常数，α，β，γ，δ为实数。将式(12)取成对数形式，即

logΠ5=logC+αlogΠ1+βlogΠ2+γlogΠ3+δlogΠ4

(13)

在双对数坐标图中，式(13)对应于直线，其中的logC是直线的截距，α，β，γ，δ则是斜率，这些待定常数均可由模拟实验数据来确定。以确定α值为例，由于每个相似准数都是独立的，因此在相似准数Π2、Π3、Π4保持不变的实验条件下，将Π5视为Π1的函数，可以将式(13)整理成如下形式：

logΠ5=logC′+αlogΠ1

在整理模拟试验数据时，针对不同的Π1可以在双对数坐标图中做出一条直线，由直线的斜率可确定α值，由其截距则可确定C′值，式(12)中的其它待定常数可依此方法获得。

式(12)对气淬粒化的原过程同样成立，此式以幂次形式反映了钢渣粒化度与其控制参量间因果关系，是具有经验性质的表达式。

3.2获得气淬工艺最佳控制参数的模拟实验方案

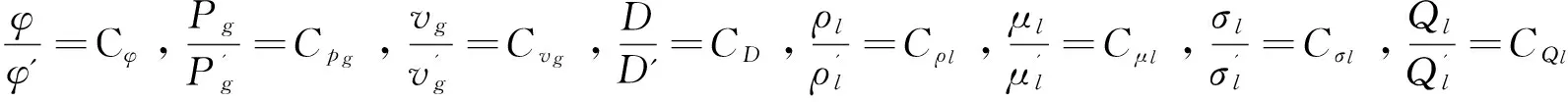
(14)

根据式(4)及式(6)，得：

(15)

同理，由式(7)～(10)、(14)可得：

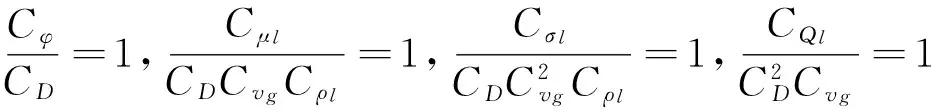
(16)

式(15)、式(16)给出的各个比例系数之间的关系式反映了影响钢渣粒化效果的主要因素之间的制约关系，其中Cρl、Cμl、Cσl的大小可由液态钢渣与模拟实验中的钢渣模型的本构参数来获得，因此可将它们视为已知量。于是，由式(15)、式(16)还可获得其余5个比例系数与3个已知量Cρl、Cμl、Cσl的关系：

(17)

(18)

(19)

(20)

能够使钢渣得到充分粒化、颗粒分布较为均匀并且粒化度符合气淬工艺要求的pg、vg、D值为最佳控制参数。由于控制参数pg、vg、D的取值与转炉产生的钢渣流量Ql以及尾渣粒化度φ的设计要求密切相关，因此，模拟实验应在对钢渣流量Ql的取值范围做出合理预设的前提下，再根据尾渣粒化度φ的设计要求，由

(21)

(22)

(23)

(24)

(25)

计算得到。

4 结论

本项研究围绕气淬钢渣的粒化度问题，运用量纲分析理论，分析了钢渣的粒化度与各种控制参量的关系，并为获得这一关系及气淬工艺的最佳控制参数提出了模拟实验方案。

[1]冷光荣，朱美善. 钢渣处理方法探讨与展望[J]. 江西冶金, 2005，25(4)： 44-47.

[2]李彬，许玉真. 采用钢渣替代铁矿石配料生产硅酸盐水泥熟料[J]. 水泥，2008，(4)：24-25.

[3]邢宏伟，魏航宇，胡长庆. 高炉渣余热回收探讨[J]. 河北冶金， 2008，(4):87-89.

[4]王少宁, 龙跃, 张玉柱, 等.钢渣处理方法的比较分析及综合利用[J]. 炼钢, 2010，26(2):75-78.

[5]龙跃. 气淬液态钢渣粒化机理及应用研究[D]. 沈阳: 东北大学, 2011.

[6]郭秀键.钢渣处理及资源化综合利用工艺[J]. 有色冶金设计与研究，2012，33(6):17-19.

[7]谈庆明.量纲分析[M] .合肥：中国科学技术大学出版社，2007:12-19.

[8]赵凯华.定性与半定量物理学[M].北京：高等教育出版社，1994：63-100.

[9]王丰.相似理论及其在传热学中的应用[M].北京：高等教育出版社，1990：58-96.

[10]杨世铭，陶文栓.传热学[M].北京：高等教育出版社，2006：229-242.

[11]F.P.Incropera，D.P.DeWitt，T.L.Bergman，等.传热和传质基本原理[M].北京：化学工业出版社，2014：214-239.

[12]Л.И.谢多夫.力学中的相似方法与量纲理论[M].北京：科学出版社，1982.

Application of Dimensional Analysis in Granulation Degree of Steel Slag by Gas Quenching

WEI Huan, CHANG Jin-cai, BO Hui-feng

(College of Science, North China University of Science and Technology, Tangshan Hebei China, 063009)

gas quenching granulation; granulation degree; dimensional analysis; theory; the physical similarity principle; similarity criterion

Gas quenching is a novel process for slag granulation in the steel industry which has drawn research interest for potential applications. One of the major goals is to achieve an optimal granulation degree of the slag by gas quenching. Focusing on this issue, a theoretical study is conducted by employing dimensional analysis theory in this research. The correlations between slag granulation degree and various parameters during gas quenching are discussed by dimensional analysis theory. A simulation experimental scheme for the correlations and optimal control parameters of gas quenching process is proposed.

2095-2716(2016)03-0014-06

TF741.3+2

A