压缩感知及其在地震勘探中的应用

王华忠,冯　波,王雄文,胡江涛,李　辉,刘少勇,周　阳

(同济大学海洋与地球科学学院波现象与反演成像研究组,上海200092)



压缩感知及其在地震勘探中的应用

王华忠,冯波,王雄文,胡江涛,李辉,刘少勇,周阳

(同济大学海洋与地球科学学院波现象与反演成像研究组,上海200092)

压缩感知思想在油气勘探领域已经受到了充分的关注。主要体现在两个方面,一个是与随机采样有关的随机地震数据采集系统的设计与评价、同时源激发的混叠数据分离、空间非规则数据的规则化、地震数据的去噪和地震数据压缩(传输)等;另一方面是地震数据的特征表达、模型参数(如速度模型参数)的特征表达、模型特征表达情况下的地震波正演模拟以及对应的稀疏反演方法(包括多尺度反演方法)。前者可以直接借鉴信号和图像处理领域发展的各种方法;后者需要勘探地球物理学家及相关领域研究人员提出合适的思想和方法。来自以沉积地层为主的地下介质中的反射(绕射)波场是有特征的或可压缩的;以层状地层为主的模型参数也是可压缩的。这是压缩感知方法能用于地震勘探的基础。首先简述了压缩感知的基本思想，指出它是一套随机采样理论。然后阐述了无论是叠前地震数据或是叠前偏移成像结果都是可以稀疏表达的，压缩感知理论可以在地震勘探中得到有效应用。接着从随机采样、同时源激发的混叠数据的分离、高维数据规则化方面展示了压缩感知思想的应用。关于随机采样，指出当前地震数据采集的技术重点应该是更高效地实现“两宽一高”的数据采集。最后列举了压缩感知思想在特征数据提取、编码炮集成像和特征波场成像中的应用。

信号和图像的特征表达;稀疏与冗余表示;压缩感知;随机采样;L1/L0范数反演

1　压缩感知思想

压缩感知的基本思想是假定实测数据中包含稀疏特征信号,选择合适的基函数能够抽取或表达这样的稀疏特征。所谓稀疏就是信号投影到基函数空间中,有有限个数的、幂指数衰减的投影系数值。可压缩性指的是可以用这样的投影系数值及对应的基函数的线性组合很好地表达原信号。在此基础上,可以用随机采样的方式(不必按香农(Shannon)采样定律)对信号进行稀疏采样(此处与稀疏的特征不同)。这个随机采样的过程可以认为是感知信号特征的过程。与Shannon采样相比,此处的随机采样可以仅仅采集很少的样点。相比于Shannon采样,这也是一种压缩采样(此处与信号的可压缩性不同)。关键是能否实现对连续信号的有效(满足一定精度的)恢复。Shannon采样期望实现对连续信号的精确恢复;压缩感知框架下的随机采样期望实现对连续信号的按精度要求的恢复。信号恢复问题一般地提为L1范数下的上述投影系数值的估计问题(当然也可以提为L2,L0甚至Lp范数下的估计问题)。此为压缩感知思想的简洁描述。

假定存在可以被压缩的信号m,选取基函数族,形成变换矩阵Φ,列向量代表基函数。期望列向量组成的基函数族是正交的基函数族。为了更稀疏的表达,可以选择框架基来表达信号:

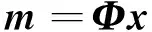
(1)

式中:向量x代表信号矢量在基函数族上的投影,也是压缩感知方法要估计的参数。它具备可压缩性特征,意指它具有幂指数衰减特征[1]。上式是信号预测关系式。

为了与随机观测的实测信号对应,引入随机采样算子R,预测并随机采样后的信号表示为:

(2)

与规则(或连续)信号相比,随机采样后的信号dcal的采样点数很稀少。这正是压缩感知采样与Shannon采样的区别所在。但是,压缩感知采样必须随机。随机采样感知到信号特征的概率要大于稀疏均匀采样,随机采样可以更好地在变换域进行连续信号的恢复。CANDÉS等[2]给出的RIP(Restricted Isometry Property)原则试图给出随机采样与连续信号可恢复性之间的定量标准。

(1)式和(2)式合并,预测并随机采样后的信号表示式变为:

(3)

式中:矩阵A被称为感知矩阵。实测数据dobs包含信号和噪声,往往假设噪声满足加性高斯分布。基于(3)式,由随机采样结果dobs估计向量x是一个反问题。一般地,仅仅估计x的具有比较大值的、有限的分量个数。这可以提为L2,L1或L0范数下的估计问题。L1范数下的估计应用最为广泛,因为这样的估计方法既是凸的,又保持一定的稀疏性。估计出向量x后,可以由(1)式恢复规则信号。此过程当然也可以进行去噪声、数据规则化和数据压缩。

L1范数下的反问题的提法为:

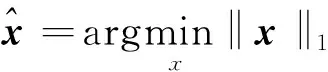
(4)

反问题的解法主要有:迭代再加权(IRLS)法、稀疏重构梯度投影(GPSR)法、SPGL1法、Bregman迭代方法、分裂Bregman(Split Bregman)迭代方法等[3-4]。

当前,Robust_PCA方法(Principal Component Analysis,PCA)代表了一类对噪声的非高斯假设方法,在噪声稀疏分布假设下发展了有效的信号和图像处理方法[5]。

很显然,实测数据中的噪声特征、信号m所具备的稀疏特征、变换矩阵的选择和随机采样矩阵的确定,以及所用的反演方法,一起决定了信号估计和恢复的精度。事实上,实际地震勘探中,信号m中的噪声对于信号的可恢复性有重大影响。相比较而言,将压缩感知的思想应用于采样和恢复时,比Shannon采样更难把握。这也是随机采样难于在地震勘探中迅速推广的原因。

2　反射波场和模型参数的稀疏特征及可压缩性

我们把勘探地震所面对的地下介质抽象为广大的、横向缓慢变化的沉积层中分布着由于火山活动、后期地质构造运动和其他地球动力运动引起的小尺度速度异常体(譬如地震勘探中的绕射地质体)。像断层、裂缝、地层尖灭、粗糙不整合面、孔洞等(大)小尺度的地质异常体是常见的油气运移通道和/或储集体,对它们的刻画和描述是油气资源勘探的重要目的。针对这样的介质情况,我们提出如下的抽象:地下介质的速度场可以分为背景速度加反射界面处的速度扰动。可用(5)式表示:

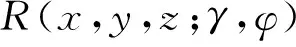
(5)

地震数据中不同偏移距接收到的反射同相轴的到达时间取决于背景速度vB(v,y,z)+δvB(v,y,z)或vB(v,y,z);同相轴上的反射波振幅取决于反射界面处波阻抗的变化或(角度)反射系数R(x,y,z;γ,φ)。不同偏移距的数据包括透射波数据(直达波和回折波(Diving Wave))和反射波数据(一次反射波和多次反射波)。当然,也包括其它更复杂的波现象,但是,目前主要利用透射波和反射波数据进行反演成像。上述观察决定了地震波反演成像的基本方法。

叠前地震数据可以抽象地描述为:将地表(也可以是井中或海底(OBC)等处)观测的地震信号视为以旅行时、炮检点坐标(或中点半偏移距)为变量的函数,它的基本特征应该是时距关系规定的、带限反射子波表现出的同相轴,叠加上一定分布特征的随机噪声(当然,也可能有不同原因产生的相干噪声)。速度(和各向异性参数)场的背景部分决定同相轴出现的位置,Q值和波阻抗变化决定反射子波的相对振幅。这样的观测决定了地震数据采集、数据规则化和去噪声可以利用压缩感知的思想,因为地震数据具有稀疏(局部线性)特征且可以被压缩。这样的观测也说明了叠前地震信号的特征与地震反射界面(像)的特征紧密相关。

因此,基于特征波场的数据预处理和反演成像具有勘探地震学物理基础。

3　随机采样思想在勘探地震中的应用

3.1地震数据随机采样

根据前两节的分析,压缩感知的思想可以被用在随机采样上,因为地震数据具备稀疏、可压缩性特征。一般地,随机采样是指炮点或检波点的空间随机采样。但是,至少目前的硬件条件,远远不适应炮点或检波点的随机布设。这也说明了目前发展独立检波器、独立(小的)震源的必要性。另一个更难以把握的问题是:由于地下介质性质(主要是速度场)横向空变可能比较剧烈,导致地震波场特征空变严重,如何设计出一个最佳的随机采样方案才能保证恢复的规则数据能很好地满足后续的精确反演成像的要求？RIP准则并没有很好地回答这个问题[2]。实质上,关于如何构建变换矩阵Φ[6]和随机采样矩阵R[4],目前的理论还没有转化为实用的方法。而仅仅考虑无假频采样的Shannon采样思想在设计观测系统时要容易得多。

我们认为,当前地震数据采集的核心问题应该是如何能真正实现“两宽一高(宽频带、宽方位和高密度)”采样,满足油气储层识别、定位、描述和评价的要求。只有在此基础上,才能开展基于压缩感知的随机采样,以提高采集效率并同时降低采集成本。

真正实现“两宽一高”地震数据采样首要的问题当然是完善目前的采集硬件。独立的震源和独立的检波器是最基本的要求。宽带震源(或多频带组合震源)及宽频响应检波器是必要的。在一个探区内,事先把这些独立的震源和检波器随机放置好,然后进行同时源激发采样,会达到非常高的采集效率。但是,目前还无法做到这一点。当前的地震数据采集,一个趋势是以陆上无线检波和海底节点(OBN)观测为代表的独立震源和独立检波观测方式,但目前它还在按Shannon采样原则布置炮检点。这样的采集方式与同时源激发相结合,试图实现宽方位观测。只要有足够多的无线检波器(陆上)或节点个数(海上),它当然也可以很好地兼顾高密度观测。高密度观测的实现非常依赖于炮点数的增加,这是同时源激发采集提高效率的自然要求。另一个趋势是增加陆上和海上单炮激发的带道能力,但是震源和检波器不是独立的,有线连接在一起。这样做的缺陷是很难真正地、高效率地实现宽方位和高密度观测,一定会被独立震源和独立检波的观测方式所取代。

我们认为,只有在独立震源和独立检波器基础上形成的观测系统才能最佳地与压缩感知的随机采样方式结合在一起形成未来的地震数据采集系统。期望震源具有宽频特征(或组合震源具有宽频特征)、自主移动特征及小型化(廉价)特征;检波器具有独立特征、无线互联特征、自主移动特征、宽频响应特征及小型化(廉价)特征。

事实上,当前典型的、基本能高效实现的“两宽一高”地震数据采集的观测系统应该首推海上的Coiling(及Quad)观测系统。但是,上述采集方式能高效实现的主要原因在于同时源激发,而不是随机空间采样,至少Coiling(及Quad)观测系统并没有刻意追求随机空间采样[7]。

我们认为,在当前硬件技术发展不满足要求的条件下,与其把精力放在基于压缩感知的随机采样上,不如放在如何用同时源激发提高宽方位高密度采样的效率上。同时源激发是目前提高“两宽一高”地震数据采样效率的切实可行的方法。即便是同时源激发数据采集也有很多问题要解决,譬如如何更好地设计同时源激发方案能更高效地进行采集,并能更彻底地分解混叠数据。

3.2同时源激发数据的解混叠

此处,我们避开同时源激发高效采集方案的设计问题,仅仅讨论混叠数据的分离方法。将混叠地震数据表达成:

db=Td=TΦx=Ax

(6)

式中:db是采集到的混叠数据;T是随机编码矩阵;d为常规未混叠的单炮;x是要估计的变换域的投影值。

提出的解混叠问题为:

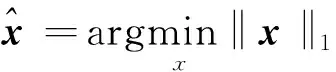
(7)

求解(7)式可以实现同时源观测数据的解混叠。但由于随机编码矩阵的形态很差，逆根本不存在，直接解(7)式定义的反问题不能很好地实现解混叠。

实际上，同时源观测数据的解混叠过程一般是按去噪的方式进行的。同时源地震激发时，副炮的激发时间是随机的，空间位置随机也可以起到相同的作用，按主炮将地震数据抽成譬如共偏移距道集，副炮中的同相轴会表现出随机性，类似随机噪声，可以用去噪的方式去除这些所谓的随机噪声，将主炮数据分离出来。由于一次去噪往往不彻底，一般设计一个迭代算法，将噪声去除干净。

图1展示了混叠数据分解的结果。混叠数据分解的基本过程是:首先对数据进行伪解码,就是数据重排,按一个选定的“主炮”进行数据排序,一般地排成共偏移距道集,其它“副炮”产生的数据就会表现出随机性。然后,利用设计的稀疏反演滤波方法滤除随机噪声,“主炮”的数据就被恢复出来。上述过程的实现方式很多,Robust_PCA方法是很好的选择[3]。图1a展示了未混叠的数据;图1b是混叠炮集;图1c就是用(6)式和(7)式表述的思想进行解混叠后的单炮数据。

图1　混叠数据分解的结果a 未混叠的单炮记录; b 混叠的单炮记录; c 解混叠后的单炮记录

3.3地震数据规则化与去噪

针对空间不规则采样(可以视为随机采样),如何更好地进行地震数据的规则化,可以视为压缩感知思想在勘探地震中的典型应用。甚至高维数据的去噪声问题,也可以归结为(4)式,只不过此时采样矩阵不再是随机的。在此意义下,地震数据的压缩(传输)也可以归结为压缩感知思想在勘探地震中的一种典型应用。实质上,高维数据规则化、去噪声和数据压缩,这些都是同一类问题,可以放在一起,用一个统一的框架来解决。这个统一的框架可以说就是所谓广义的压缩感知。

选择Fourier基函数,我们将高维地震数据规则化问题提为:

(8)

式中:A是前述的感知矩阵;W是Radon谱,引入W的目的是抗假频。在谱域进行残差估计,主要是计算方便,更容易考察估计结果的信噪比。(8)式用匹配追踪的方法求解,我们称此方法为加权匹配追踪(Weighted matching pursuit,WMP)。

图2a展示的是规则数据,图2b是非规则数据;图2c是利用(8)式进行的数据规则化结果,图2d是用抗泄漏的Fourier变换方法得到的数据规则化结果。二者的主要差异在于是否用Radon谱进行约束。Radon谱约束的主要目的在于更好地反假频。

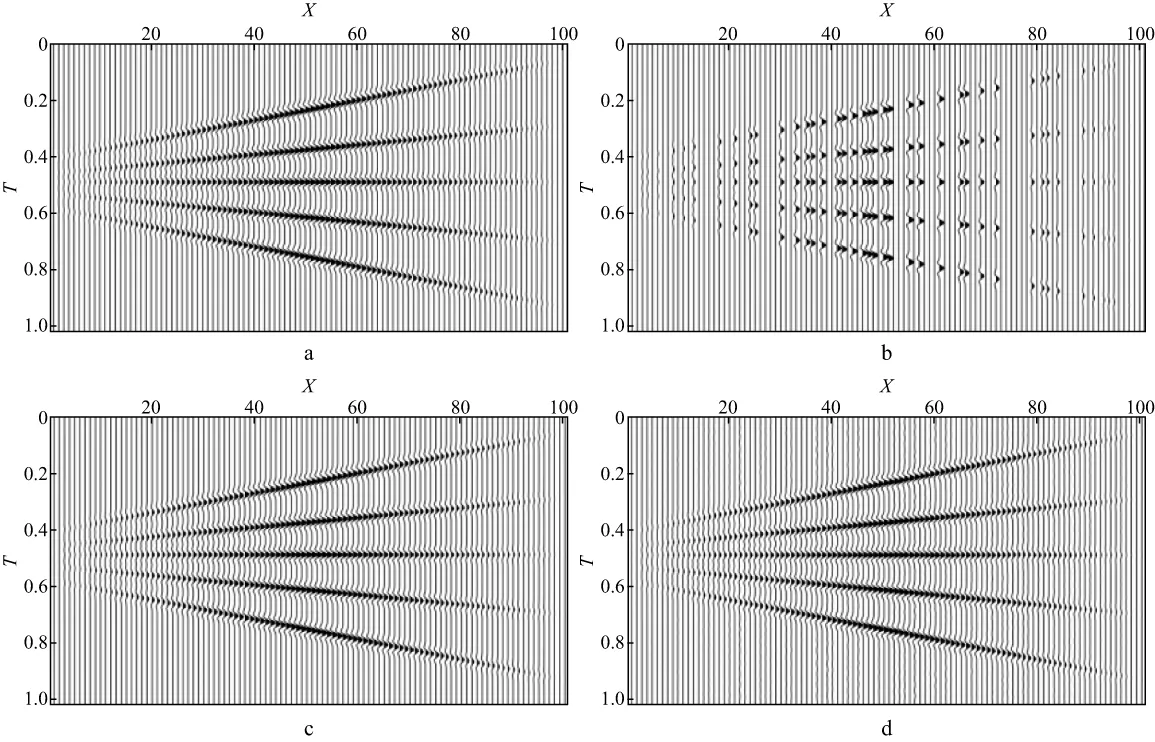
图2　两种方法得到的数据规则化结果a 规则数据; b 非规则数据; c WMP方法规则化; d 抗泄漏的Fourier变换(ALFT)方法规则化

4　特征波场提取与特征波成像

前已述及,地震数据的像(角度成像道集)与叠前地震数据本身都是有特征的、可以进行压缩的。压缩感知思想可以用在地震波反演成像中。有多种方式将压缩感知用于地震数据的成像过程。最常用的是用随机编码炮记录进行地震波偏移或反演成像,加快偏移或反演成像的计算效率。编码炮偏移可以实现的基础是成像结果(像)具有特征。

4.1编码炮道集叠前深度偏移成像

编码炮数据的最小二乘偏移可以表示成:

(9a)

式中:C为随机编码矩阵。随机编码的方式决定了编码炮偏移的效率以及成像结果中Cross-Talk噪声压制的程度。(9a)式的解可以表示为:

(9b)

式中:CTC是编码相关矩阵。选择合适的编码矩阵可以使得编码相关矩阵接近单位矩阵。当编码相关矩阵等于单位矩阵时,编码炮偏移就与常规单炮偏移完全等价。编码炮偏移的目标就是选择合适的编码矩阵使得在成像效率和成像效果之间达到最佳平衡。图3a是真反射系数;图3b是随机常规单炮道集逆时偏移(RTM)结果;图3c是常规单炮最小二乘RTM(LS_RTM)结果;图3d是随机编码超炮集的LS_RTM结果。图3d所示的随机编码超炮集的LS_RTM结果与图3c所示的常规单炮LS_RTM结果相比基本相同,但计算效率大为提高。

4.2特征波场提取与特征波场成像

我们提出了特征波场及特征波成像的概念[10]。特征波场定义为:局部时间空间域的单震相的方向带限波场。目的是利用特定的波场进行有针对性的成像。

一般地,特征叠前地震数据可以表达成:

(10)

特征像可以表达成:

(11)

(10)式表达的数据可以视为局部平面波,还可以进一步表达为高斯波包,更进一步可以表达为空间到达时或与相位有关的空间到达时。我们提出特征表达波场的目的不是利用压缩感知思想处理数据,而是试图建立起特征波场与特征像之间的更直接的关系,有利于后续的层析成像和最小二乘偏移。

我们首先构建了实测数据与局部平面波之间的预测关系:

d(x,ω)=B(x,p,ω)x(p,ω)

(12)

(12)式是空间阵列分析、空间谱分析中典型的预测模型[8]。基于此预测模型可以建立如下反问题:

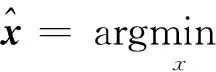
(13)

式中:B为感知矩阵。求解(13)式所示反问题得到

局部平面波的稀疏估计[11-12]。图4a是合成的具有局部平面波特征的数据;图4b是L2范数下估计的平面波场;图4c是L1范数下估计的平面波场。可以看出L1范数下局部平面波估计结果的稀疏性大为提高。

图3　真反射系数(a),常规RTM结果(b),常规单炮LS_RTM结果(c)以及随机编码超炮集LS_RTM结果(d)

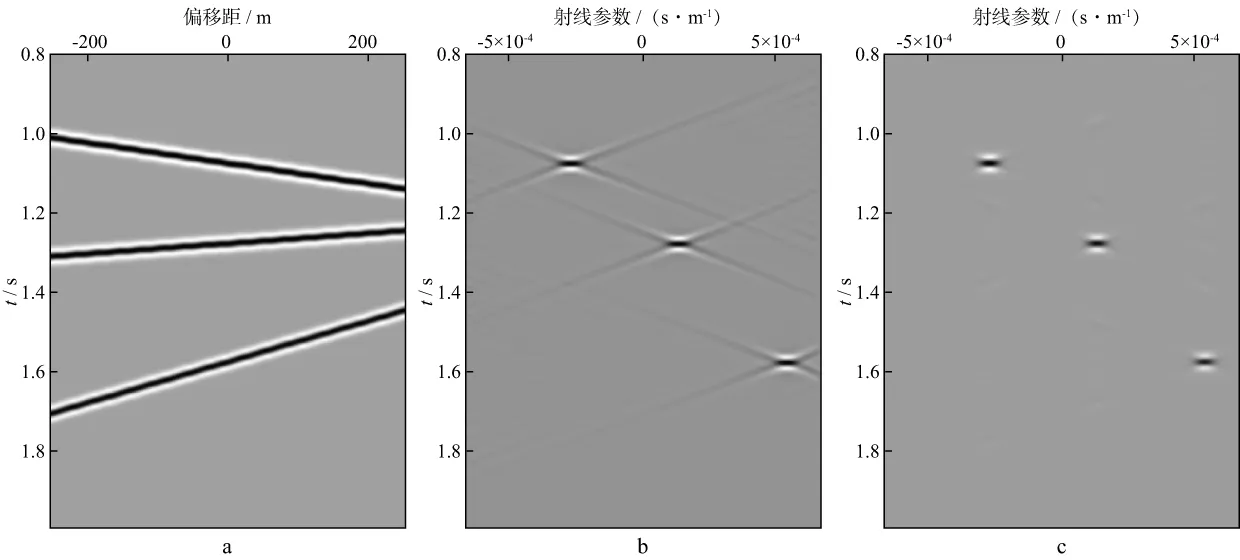
图4　合成波场(a),L2范数下估计的平面波场(b)和L1范数下估计的平面波场(c)

针对上述特征波场分解,我们构建了特征波场Beam成像方法和特征波场高斯波包成像方法[13]。目的是将特征波场更直接地映射为地下构造的像。更进一步地,也可以进行层析反演成像。图5a是理论速度模型;图5b是特征波场高斯波包叠前深度偏移成像结果。

更进一步地,我们希望做的工作是首先抽取参数模型的某一个尺度的特征点,然后做基于特征点的波动方程模拟,接着实现该尺度下的参数反演。逐渐加细尺度,反演越来越详细的模型参数。另一方面,针对当前的FWI难以应用于实际数据的情况,我们提出基于特征波场的逐步线性化的反演成像方法,即:波动理论的(与相位有关的)透射波到达时层析结合波动理论的(与相位有关的)反射波到达时层析以及LS_RTM,期望通过这种技术组合的方式推进FWI技术的实用化。

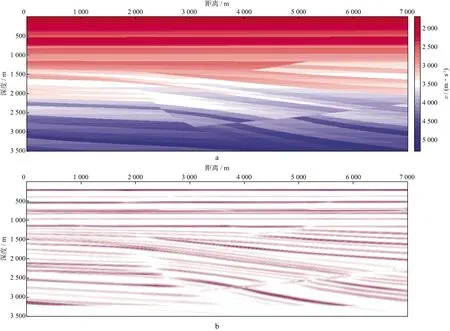
图5　理论速度模型(a)及特征波场高斯波包偏移成像结果(b)

5　结论

严格地讲,压缩感知是一个数据采样理论框架。但是在地震数据采样的应用中,我们认为地震数据采集当前的核心问题应该是如何能真正实现“两宽一高”采集,满足油气储层的识别、定位、描述和评价要求。只有在此基础上,才能开展基于压缩感知的随机采样,以提高采集效率并同时降低采集成本。目前震源和检波器技术还没有发展到与压缩感知随机采样相适应的程度。地震数据采样技术发展的重点依然在于如何用同时源激发的方式更好地实现“两宽一高”采集。

尽管压缩感知方法具有明晰的思想,并已有若干有效的应用实例,但是依然存在需要深入研究的问题。第一个问题是随机采样方式与规则数据可恢复性之间缺乏可操作性的评价方法,即究竟如何进行随机采样才能保证有较高的信号恢复精度,缺乏可操作性的评价手段。因为基于感知信号特征的随机采样方法要依据信号特征而变化,而信号特征事先是未知的。RIP指标并不能直接用于地震勘探中随机采样方式的构建和评价。这应该是随机采样方法不能贸然实用的原因。第二个问题是如何基于模型参数(譬如反射系数)的特征表达,构建相应的基于特征表达的波传播方法及数值模拟方法,实现多尺度的模型参数反演。HERRMANN等虽然提出了模型稀疏表达下的反演成像方法,但是他们的工作回避了模型的多尺度表达以及模型特征表达下的正演计算。对于模型参数特征表达情形下的反演成像而言,这两点才是最关键的、最能体现勘探地震或地球物理专业特点的地方。

压缩感知思想在勘探地震中的应用除了上述两点外,其它的思想和方法的借用都是顺理成章的。本文中列出的若干实例说明了这一点。

我们认为基于模型参数的多尺度稀疏表达、与之对应的波动方程求解、L1范数下的稀疏反演成像应该是压缩感知思想方法在勘探地震中重要且长期的研究方向。

[1]DONOHO D L.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306

[2]CANDÉS E J,TAO T.Decoding by linear programming[J].IEEE Transactions on Information Theory,2005,51(12):4203-4215

[3]ELAD M.Sparse and redundant representations:from theory to applications in signal and image processing[M].New York:Springer,2010:1-376

[4]PATEL V M,CHELLAPPA R.Sparse representations and compressive sensing for imaging and vision[M].New York:Springer,2013:1-102

[5]CANDÉS E J,LI X,MA Y,et al.Robust principal component analysis?[J].Journal of the ACM,2011,58(3):11

[6]MALLAT S.A wavelet tour of signal processing,third edition:the sparse way[M].Burlington:Academic Press,2008:1-832

[7]MOLDOVEANU N,KAPOOR J.Quad coil towed streamer marine acquisition[J].Expanded Abstracts

of 85thAnnual Internat SEG Mtg:81-85

[8]MANOLAKIS D G,INGLE V K,KOGON S M.Statistical and adaptive signal processing:spectral estimation,signal modeling,adaptive filtering and array processing[M].Boston:Artech House,2005:1-816

[9]HERRMANN F J,WANG D L.Seismic wavefield inversion with curvelet-domain sparsity promotion[J].Expanded Abstracts of 78thAnnual Internat SEG Mtg,2008:2497-2501

[10]王华忠,冯波,刘少勇,等.叠前地震数据特征波场分解、偏移成像与层析反演[J].地球物理学报,2015,58(6):2024-2034

WANG H Z,FENG B,LIU S Y,et al.Prestack data based characteristic seismic wave decomposition,its migration and tomography[J].Chinese Journal of Geophysics,2015,58(6):2024-2034

[11]胡江涛,王华忠,王雄文.拉东谱约束的射线束形成方法及应用[J].石油物探,2013,52(4):335-338

HU J T,WANG H Z,WANG X W.Beam forming by Radon spectrum constraint and its application[J].Geophysical Prospecting for Petroleum,2013,52(4):335-338

[12]王雄文,王华忠.基于压缩感知的高分辨率平面波分解方法研究[J].地球物理学报,2014,57(9):2946-2960

WANG X W,WANG H Z.A research of high-resolution plane-wave decomposition based on compressed sensing[J].Chinese Journal of Geophysics,2014,57(9):2946-2960

[13]李辉,冯波,王华忠.波场模拟的高斯波包叠加方法[J].石油物探,2012,51(4):327-337

LI H,FENG B,WANG H Z.A new wave field modeling method by using Gaussian Packets[J].Geophysical Prospecting for Petroleum,2012,51(4):327-337

(编辑：朱文杰)

Compressed sensing and its application in seismic exploration

WANG Huazhong,FENG Bo,WANG Xiongwen,HU Jiangtao,LI Hui,LIU Shaoyong,ZHOU Yang

(WavePhenomenaandInversionImagingGroup(WPI),SchoolofOceanandEarthScience,TongjiUniversity,Shanghai200092,China)

Compressed sensing (CS) has been given full attention in the domain of oil and gas seismic exploration.The idea of CS is mainly implemented in two aspects,one is random-sampling based applications,such as seismic acquisition design and evaluation,de-blending of simultaneous-source data,regularization of seismic data,denoising and compression of seismic data; the other is the characteristic expression of data and model parameters,and the corresponding forward modeling and sparse inversion methods (including multi-scale inversion).The former one can be solved by using various methods developed in signal and image processing fields while the latter one need geophysicists to develop new ideas and methods.Both the reflection scattering waves and layered models are compressible,which make is possible for the successful application of CS in exploration seismology.The basic idea of CS is concisely sketched and it is pointed out that CS is a theoretical frame of random sampling.And then we demonstrate that both the prestack seismic data and its migration results can be sparsely expressed.CS can be reasonably used in seismic exploration.We show its applications in random sampling,de-blending of simultaneous-source data and regularization of multi- dimensional seismic data.It is indicate that the current seismic data acquisition technology development should be focused on how to truly implement the so-called “broadband and wide-azimuth and high sampling density” seismic data acquisition.At last,the application of CS in characteristic data extraction,encoding shot gathers imaging and characteristic wavefield imaging are enumerated.

characteristic expression of signal and image,sparse and redundant representation,compressed sensing,random sampling,L1/L0norm inversion

2016-02-28;改回日期：2016-03-22。

王华忠(1964—),男,教授,主要从事地震波传播、地震数据分析和地震波反演成像方面的研究工作。

国家自然科学基金项目(41374117)和国家科技重大专项(2011ZX05005-005-008HZ,2011ZX05006-002,2011ZX05023)联合资助。

P631

A

1000-1441(2016)04-0467-08DOI:10.3969/j.issn.1000-1441.2016.04.001

This research is financially supported by the National Natural Science Foundation of China (Grant No.41374117) and the National Science and Technology Major Project of China (Grant Nos.2011ZX05005-005-008HZ,2011ZX05006-002,2011ZX05023).