一种体现孔隙形态影响的四参数孔隙度反演方法

郭继亮,李宏兵,李　明,张　研,李劲松,于　豪,刘晓虹

(中国石油天然气股份有限公司勘探开发研究院,北京100083)



一种体现孔隙形态影响的四参数孔隙度反演方法

郭继亮,李宏兵,李明,张研,李劲松,于豪,刘晓虹

(中国石油天然气股份有限公司勘探开发研究院,北京100083)

传统的测井孔隙度反演方法在反演复杂孔隙形态地层的孔隙度时往往存在偏差。孔隙形态的影响可以利用等效介质模型体现,提出了一种四参数孔隙度反演方法,即,引入差分等效介质(Differential Effective Medium,DEM)模型,将孔隙度反演与孔隙形态的影响相结合,利用中子、密度、纵波时差和横波时差四个参数实现地层的孔隙度和孔隙纵横比的同步反演。首先利用中子、密度和纵波时差反演地层孔隙度初值,通过DEM模型求取孔隙纵横比初值;而后利用纵波速度、横波速度和体积密度信息同步反演声学孔隙度和孔隙纵横比;最后综合利用中子、密度、纵波速度和横波速度数据,对地层孔隙度和孔隙纵横比进行同步反演。以西南某探区深层白云岩地层孔隙度反演为例,比较了不同孔隙度反演方法的效果,验证了四参数孔隙度反演方法的有效性。

孔隙纵横比;孔隙度;差分等效模型;四参数孔隙度模型;同步反演

孔隙度测井中,孔隙度是测井解释、储层评价、流体预测和储量计算的重要依据[1-3]。因此,孔隙度的求取非常关键。传统三参数孔隙度反演方法基于地层介质纵波速度、电子密度以及地层氢含量与孔隙空间大小的线性关系,利用声波时差、体积密度和中子孔隙度最小二乘拟合计算地层孔隙度,这种方法在砂岩地层中取得了良好的应用效果[4-7]。3个地层物性参数中,中子孔隙度和体积密度为标量,岩石基质不变的条件下,其大小仅取决于孔隙空间大小;地层速度为矢量,声波测井数据中包含地层高频速度信息,反映了地层孔隙结构对弹性特征的影响。井中的孔隙度-速度关系是地震岩石物理建模、储层参数反演和流体预测的基础[8-9]。地层孔隙度反演也是建立地层孔隙结构与弹性特征之间联系的过程[10-11]。WYLLIE等[12],RAYMER等[13],RAIGA-CLEMENCEAU等[14]和李宁[15]分别给出了声波孔隙度计算公式,在孔隙度较高且孔隙形态较简单的情况下应用效果均较好,但这些计算公式都未体现孔隙结构对地层速度的影响,无法解释同一孔隙度条件下速度的散布现象。

随着碳酸盐岩勘探开发程度的深入,在孔隙结构较复杂的地区,地层速度不仅受孔隙度影响,还受其它诸如孔隙结构的影响,其中最主要的就是孔隙形态[10,16]。这使得传统三参数孔隙度反演的效果受到影响,一般的解决方案是使用中子-密度双参数来反演孔隙度,从而避免复杂孔隙结构引起反演结果的偏差。双参数孔隙度反演方法可以得到较准确的孔隙度,但反演结果不反映地层的弹性信息,给进一步的井震结合带来困难[17-19]。孔隙纵横比是表征孔隙结构的主要参数,与孔隙度共同决定孔隙对介质声学特征的影响[20-22]。孔隙纵横比是岩石内孔隙形态的综合体现,二维平面内可以表示为等效椭圆孔隙的短轴和长轴之比[23]。孔隙纵横比对中子测井和密度测井没有明显的影响,其作用体现在地层速度上。

差分等效介质(DEM)模型是一种描述岩石弹性特征和孔隙结构关系的岩石物理模型,可以定量描述岩石干燥骨架弹性特征与其孔隙度和孔隙纵横比的关系[24]。利用DEM模型,向基质骨架中逐次加入微量不同形态的孔隙最终获得地层介质干骨架弹性模量,进而获得地层介质速度[25-27]。该方法在刻画复杂孔隙结构碳酸盐岩地层弹性特征方面效果较好,可以准确给出不同纵横比的孔隙对地层介质弹性特征的影响[28-31]。DEM模型具有高精度高稳定性的特点,其局限性在于模型的隐式表达形式使其运算效率较低[32-33]。ZIMMERMAN[26],BERRYMAN等[34]以及LI等[35]先后利用数值微分计算和模量比近似等方法得到了DEM模型的弹性模量显式表达式。LI等还采用变量置换和微分高阶展开的方法分别给出了4种基本孔隙形态和多重孔隙形态DEM模型弹性模量显式表达形式,并将其用于地层横波预测[36-39]。DEM公式显式表达式的提出大大提高了该方法的计算效率,扩展了其应用范围。

本文在考虑孔隙纵横比对地层速度影响的基础上,利用DEM模型描述孔隙度和孔隙纵横比对纵波速度和横波速度的影响,结合三参数孔隙度反演方法提出了四参数孔隙度反演方法,即利用纵波时差、横波时差、中子和密度信息反演受孔隙纵横比影响的地层孔隙度。将该方法应用于深层碳酸盐岩孔隙类型丰富的我国西南地区,而后对不同孔隙度反演方法反演结果的精度进行对比分析,以验证四参数孔隙度反演方法的反演效果。

1　四参数孔隙度模型

基于传统的三参数孔隙度模型,利用DEM模型描述孔隙度和孔隙形态对地层速度的影响,构建包含孔隙形态影响的四参数孔隙度模型。假设地层岩石物理体积模型由n种矿物和孔隙组成,则传统的三参数孔隙度反演公式为:

(1)

式中:ΔT,Φ和ρ分别表示纵波时差、中子孔隙度和体积密度;下角标L表示测井获得的地层参数;下角标f表示孔隙流体;下角标S代表骨架基质;设骨架由n种以上矿物组成,则下角标i代表岩石骨架中第i中矿物;Vi(i=1,2,…,n)为第i种矿物的体积含量;φ为孔隙度。去掉公式(1)中的纵波时差项就可得到中子-密度双参数孔隙度反演模型。常用的声波孔隙度反演公式中速度均为孔隙度的线性函数,如Wyllie公式和Raymer公式。虽然很多工作都证明了孔隙形态对介质弹性参数有着重要影响,但这种影响往往被忽略[10,38,40-41]。

为定量描述孔隙形态对地层速度的影响,引入孔隙纵横比参数,再利用DEM模型精确表达孔隙度和孔隙纵横比影响地层弹性模量程度。DEM模型描述了固体相态基质中加入n种不同形态包裹体后的弹性参数,每种成分均为逐次微量加入[25]。经典DEM模型表达式为:

(2)

式中:Ki和μi为第i种组分的体积模量和剪切模量;y为第i种组分的体积百分比;P*i和Q*i为第i种组分的形态因子。传统的DEM模型中目标体弹性参数K*和μ*以隐式方式存在,应用过程中一般采用递归算法离散化,计算效率较低且没有解析表达式,很难应用于反演。针对这个问题LI等[35-37]提出了针对不同孔隙形态的DEM模型显式表达式,大大提高了DEM模型的计算效率和适用性。本文采用LI等[35-37]给出的解析表达式对声波方程进行改进,单一孔隙纵横比DEM模型显式弹性参数表达式为:

(3)

(4)

式中:Kdry和μdry为岩石干燥骨架的体积模量和剪切模量;Km和μm为骨架基质的弹性模量;φ为介质孔隙度;α为表示孔隙形态的孔隙纵横比;a和b的形式为:

(5)

(6)

利用公式(3),公式(4),公式(5)和公式(6)可得到岩石干燥骨架体积模量Kdry和剪切模量μdry与孔隙度φ和孔隙纵横比α的关系,再通过Gassmann方程加入流体最终求出地层岩石的体积模量Ksat和剪切模量μsat。则地层纵波速度和横波速度即声学孔隙度模型为:

(7)

式中:ρb为介质体积密度。在声学孔隙度模型的基础上加入中子和密度信息,由中子、密度、纵波速度和横波速度4个参数共同反演地层的孔隙度和孔隙纵横比。其中孔隙度受这4个参数的影响,孔隙纵横比仅受纵波速度和横波速度的影响,其形式如下:

(8)

2　孔隙度反演方法

四参数孔隙度反演模型中,中子和密度参数为孔隙度的线性函数,纵波速度和横波速度为孔隙度和孔隙纵横比的非线性函数,因此4个物性参数与孔隙度和孔隙纵横比之间的关系为非线性关系。利用Levenberg-Marquardt法求解非线性反演方程。为了减小非线性方法对初值的依赖性,在进行孔隙度和孔隙形态联合反演时,给出较为准确的初值非常必要。反演基本流程如图1所示。

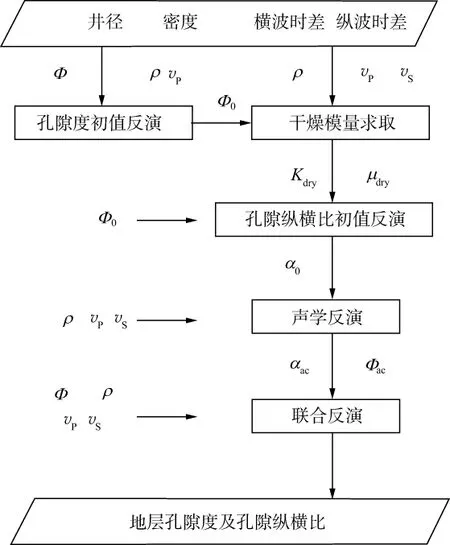
图1　四参数孔隙度模型反演流程

2.1初值反演

利用测井数据中的中子孔隙度、体积密度和纵波时差,交会计算得到地层孔隙度初值,进而利用DEM方法反演孔隙纵横比初值。

2.2声学反演

基于声学孔隙度模型,利用孔隙度初值和孔隙纵横比初值,同步反演声学孔隙度和声学孔隙纵横比。

2.3联合反演

利用四参数孔隙度模型,将声学孔隙度和声学孔隙纵横比作为反演初值,同步反演地层孔隙度和孔隙纵横比。

3　实际应用与效果分析

3.1初值反演

我国西南地区深层碳酸盐岩中孔隙类型丰富,包括溶蚀孔、基质孔和粒间孔等,孔隙纵横比不一(图2)[42-43]。将四参数孔隙度反演方法应用于该地区深层白云岩地层孔隙度和孔隙纵横比反演;对该区内MX13井,MX19井,MX203井和MX204井有岩心孔隙度数据的白云岩储层段进行孔隙度反演。

图2　研究区内MX13井储层岩心和薄片特征a 4606.10m岩心; b 4615.35m薄片; c 4614.30m岩心

研究区内地层以砂屑白云岩、残余砂屑白云岩和细-中晶白云岩为主,夹少量的灰岩和泥质,硅质含量非常少,据此建立的岩石物理体积模型如图3所示。经过矿物校正后骨架基质体积模量为94GPa,剪切模量为44GPa,密度为2.87g/cm3。

图3　研究区内岩石物理体积模型

以MX19井为例,地层中子、密度、纵波时差和横波时差的数据,以及地层三参数孔隙度数据如图4所示。其中孔隙度数据中红色线段为对应位置岩心孔隙度测量结果,蓝色曲线为三参数孔隙度反演结果,二者差异较大。将三参数孔隙度反演结果作为孔隙度反演的初值,初值是孔隙纵横比反演的必要条件,但由于其不反映地层孔隙结构特征,故存在一定偏差,仅可作为地层孔隙度的参考值。

利用测井数据中体积密度、纵波速度、横波速度和孔隙度初值反演地层的孔隙纵横比。反演的前提是获得地层岩石干燥骨架的体积模量和剪切模量,通过Gassmann方程利用孔隙度初值获得干燥骨架模量;进而反演地层孔隙纵横比初值。

利用Levenberg-Marquardt法实现孔隙纵横比的反演,其目标函数为:

(9)

式中:ρ,vP,vS为测井数据中获得的地层整体密度、纵波速度和横波速度信息;KM和μM为通过DEM模型和Gassmann方程计算获得的流体饱和岩石的体积模量和剪切模量,它们都是孔隙度和孔隙纵横比的函数,孔隙纵横比α0为反演的目标值。

反演结果即孔隙纵横比初值如图5所示,其中蓝色实线为三参数孔隙度,红点为对应的孔隙纵横比初值,绿色短竖线表示对应位置的岩心孔隙度,即实验室测出的岩心孔隙度大小。

孔隙纵横比初值是基于三参数孔隙度反演得到,因为三参数孔隙度存在偏差,所以孔隙纵横比初值也仅为地层孔隙结构特征的参考;地层孔隙度初值和孔隙形态初值的主要作用是为地层声学反演,即地层孔隙度和孔隙纵横比联合反演提供较合理的初值。

图4　测井参数及孔隙度初步反演结果(1ft≈0.3048m)

图5　三参数孔隙度(φ0)与孔隙纵横比初值(α0)

3.2声学反演

初值反演中分步求取孔隙度和孔隙纵横比的初值,声学反演利用地层的纵波速度、横波速度和体积密度信息同步反演孔隙度和孔隙纵横比。通过双参数联合反演获得的孔隙度和孔隙纵横比耦合程度进一步提高。相对于分步求取这两个参数,同步反演的结果更加准确地体现岩石孔隙结构和弹性参数之间的关系。通过Levenberg-Marquardt法实现双参数同步反演,其目标函数为:

(10)

公式(10)中各项参数意义与孔隙纵横比初值

反演的目标函数相同,区别在于反演的目标值为声学孔隙度φac和声学孔隙纵横比αac。

声学反演结果如图6所示,红色实线为声学反演得到的孔隙度φac,蓝色实线为孔隙度初值φ0(三参数孔隙度)。在有效储层部分二者差异较明显,声学孔隙度大于三参数孔隙度。与之对应的孔隙纵横比值差异较明显,蓝色散点表示的孔隙纵横比初值α0整体上低于用红色散点表示的声学孔隙纵横比αac。这也是声学反演对孔隙纵横比的进一步校正。

声学孔隙度和孔隙纵横比直观地反映了复杂孔隙结构条件下岩石中的孔隙度和孔隙纵横比对地层弹性参数的影响。这两个参数共同影响地层弹性参数,同步反演获得的两个参数同时体现它们的影响更加符合孔隙结构对地层物性影响的规律。

图6　声学孔隙度(φac)与声学孔隙纵横比(αac)反演结果

3.3联合反演

在声学反演的基础上进行四参数联合反演,即利用中子、密度测井及测井中的纵波速度和横波速度反演地层孔隙度和孔隙纵横比。联合反演是声学反演和中子-密度双参数反演的结合。与传统的三参数孔隙度反演相比,改进的孔隙度反演方法引入了横波速度,反演结果除了孔隙度外还有孔隙纵横比。联合反演依据(11)式,其目标函数为:

(11)

式中:φ4和α4为地层的孔隙度和孔隙纵横比。

图7为联合反演孔隙度与三参数孔隙度和声学孔隙度对比,其中蓝色实线为三参数孔隙度;红色实线为声学孔隙度;黑色实线为联合反演获得的地层孔隙度值;绿色竖线为对应位置的岩心孔隙度。可见,在大部分区域声学孔隙度较大;而传统的三参数孔隙度较小;四参数孔隙度居中。

联合反演得到的孔隙纵横比如图8所示,孔隙纵横比分布特征与孔隙度类似,联合反演获得的孔隙纵横比(红色散点)总体上高于初值(蓝色散点)。这种差异由对应的孔隙度差异造成,基于DEM模型,孔隙度增大使介质速度减小,而纵横比增大使速度增大,在介质速度一定时,孔隙度与孔隙度纵横比共同影响介质速度。联合反演充分体现了这两个参数的变化规律,因此获得了更加准确的反演结果。

3.4孔隙度分析

除了上述3种孔隙度(φ0,φac,φ4),对MX19井还采用了Raymer方程、Wyllie方程、中子-密度双参数方程求取了地层孔隙度分别记作φR,φW

图7　联合反演孔隙度与三参数孔隙度和声学孔隙度比较

图8　联合反演孔隙度和孔隙纵横比与初值比较

和φ2。6种孔隙度的比较如图9所示,基本都体现了地层孔隙度大小的变化趋势,但精度上各有不同,Raymer方程反演结果(φR)最大。

四参数孔隙度模型中还给出了影响介质速度变化的孔隙纵横比。MX19井中,四参数孔隙度与速度的交会图如图10所示,各个颜色的实线表示不同孔隙纵横比的速度和孔隙度关系,红色虚线表示Wyllie公式拟合速度曲线,黑色曲线表示Raymer公式拟合速度曲线。图10中孔隙度与速度关系不能简单的用Wyllie公式和Raymer公式表示,但DEM模型可利用孔隙纵横比准确表示速度和孔隙度的散布关系,即定量解释同一骨架基质条件下相同孔隙度对应不同速度的现象。速度散布是地层孔隙形态复杂的表现,也是孔隙形态对地层速度影响的表现。利用这种声学关系,结合地层体积密度和中子孔隙度反演得到的地层孔隙度具有更高的精度,而且可以充分体现地层孔隙形态对速度的影响,为地震岩石物理建模提供更加丰富的信息。

利用相同的方法计算MX13井,MX203井和MX204井的孔隙度并分析不同方法反演的孔隙度和孔隙纵横比。图11和图12 给出了这4口井分别采用Raymer方程、Wyllie方程、中子-密度双参数、中子-密度-声波三参数、声学孔隙度模型和四参数孔隙度模型反演获得的孔隙度值与相应位置的岩心孔隙度的偏差统计图和相似度统计图。偏差代表各组孔隙度与岩心孔隙度的L2范数,体现反演值与岩心孔隙度的空间距离;相似性代表各组孔隙度与岩心孔隙度的相关系数,体现反演孔隙度的分布形态特征。

图9　MX19井6种反演方法获得的孔隙度比较

通过与岩心孔隙度对比可得,四参数孔隙度具有偏差小的特征,在MX13井,MX19井以及MX204井中偏差最小,在MX203井中仅次于声学反演孔隙度,这是综合利用岩石声学特征和放射性特征的结果。三参数孔隙度、声学孔隙度和双参数孔隙度偏差中,双参数孔隙度反演方法的偏差最小;仅考虑弹性特征的声学孔隙度和忽略孔隙形态影响的四参数地层三参数孔隙度的偏差相近。而单独运用声波而未考虑孔隙形态影响的Raymer方程和Wyllie方程偏差较大,且在研究区内Wyllie方程的效果优于Raymer方程。这说明:即使多参数交会法孔隙度计算方法具有综合利用信息的优势,但在无法描述孔隙形态对介质声学特征影响的前提下,双参数孔隙度反演结果偏差更低。

相似性方面,MX13井,MX19井以及MX203井中双参数、三参数和四参数法反演结果与岩心孔隙度的相关程度均大于80%,相似性较高,而在MX204井中,这3种反演方法的相关程度也不低于75%,高于其它3种方法。其中四参数模型和双参数模型的相似性更高。依赖弹性特征的声学反演和仅仅利用纵波的反演相似性较低。综上所述,考虑孔隙纵横比影响的四参数地层孔隙度反演方法不但得到高精度的地层孔隙度值,还可以通过孔隙纵横比定量描述孔隙形态对地层介质弹性特征的影响。

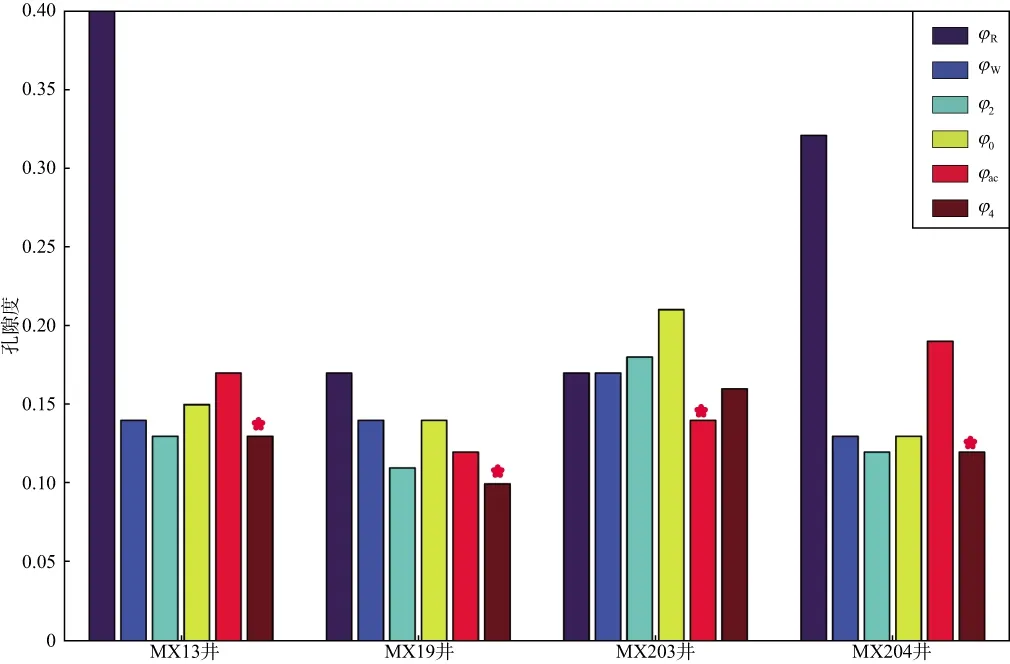
图11　不同孔隙度与岩心测量孔隙度偏差比较(星号表示偏差最小)

图12　不同孔隙度与岩心测量孔隙度相关性比较(星号表示相关性最大)

4　结论

本文提出一种四参数地层孔隙度反演方法,基于孔隙度和孔隙形态与介质弹性模量的关系,引入DEM模型,利用地层介质声学特征和放射性特征反演地层孔隙度和孔隙纵横比。将该方法应用于西南某地深层碳酸盐岩地层孔隙度反演取得了良好的效果。

1) 四参数孔隙度反演的结果与岩心测量结果符合度更高。这种符合度体现在高相关性和低偏差方面。

2) 四参数孔隙度反演获得的孔隙纵横比信息可以体现不同孔隙形态对介质弹性特征的影响,为进一步的地震岩石物理建模提供参考。

[1]DARLING T.Well logging and formation evaluation[M].Oxford:Gulf Professional Publishing,2005:1-336

[2]ETNYRE L M.Finding oil and gas from well logs[M].New York:Springer International Publishing AG,1989:249

[3]黄思静,张萌,朱世全,等.砂岩孔隙成因对孔隙度/渗透率关系的控制作用——以鄂尔多斯盆地陇东地区三叠系延长组为例[J].成都理工大学学报(自然科学版),2004,31(6):648-653

HUANG S J,ZHANG M,ZHU S Q,et al.Control of origin of pores over relationship of porosity to permeability in sandstone reservoir:a case study from Yanchang sandstone of Triassic of eastern Gansu,Ordos Basin[J].Journal of Chengdu University of Technology(Science & Technology Edition),2004,31(6):648-653

[4]SAVRE W C.Determination of a more accurate porosity and mineral composition in complex lithologies with the use of the sonic,neutron and density surveys[J].Journal of Petroleum Technology,1963,15(9):945-959

[5]张小莉,沈英,陈文学.利用测井资料分析成岩作用对储集层的影响[J].沉积学报,2000,18(1):127-131

ZHANG X L,SHEN Y,CHEN W X.Application of well logging information to analysis on the effect of diagenesis in reservoirs[J].Acta Sedimentologica Sinica,2000,18(1):127-131

[6]潘保芝,李舟波,付有升,等.测井资料在松辽盆地火成岩岩性识别和储层评价中的应用[J].石油物探,2009,48(1):48-52

PANG B Z,LI Z B,FU Y S,et al.Application of logging data in lithology identification and reservoir evaluation of igneous rock in Songliao basin[J].Geophysical Prospecting for Petroleum,2009,48(1):48-52

[7]JORGENSEN D G.Using geophysical logs to estimate porosity,water resistivity,and intrinsic permeability[M].Reston:United States Government Printing Office,1989:1-24

[8]GOMEZ C T,DVORKIN J,VANORIO T.Laboratory measurements of porosity,permeability,resistivity,and velocity on Fontainebleau sandstones[J].Geophysics,2010,75(6):E191-E204

[10]WEGER R J,EBERLI G P,BAECHLE G T,et al.Quantification of pore structure and its effect on sonic velocity and permeability in carbonates[J].AAPG Bulletin,2009,93(10):1297-1317

[11]CHILINGARIAN G V,MAZZULLO S J,RIEKE H H.Carbonate reservoir characterization:a geologic engineering analysis,Part II[M].Amstedam:Elsevier,1996:179-180

[12]WYLLIE M R J,GREGORY A R,GARDNER G H F.An experimental investigation of factors affecting elastic wave velocities in porous media[J].Geophysics,1958,23(3):459-493

[13]RAYMER L L,HUNT E R,GARDNER J S.An improved sonic transit time-to-porosity transform[J].SPWLA 21stAnnual Logging Symposium,1980:1-13

[14]RAIGA-CLEMENCEAU J,MARTIN J P,NICOLETIS S.The concept of acoustic formation factor for more accurate porosity determination from sonic transit time data[J].SPWLA 27thAnnual Logging Symposium,1986:54-60

[15]李宁.中国海相碳酸盐岩测井解释概论[M].北京:科学出版社,2013:64-67

LI N.Chinese marine carbonate log interpretation introduction[M].Beijing:Science Press,2013:64-67

[16]ANSELMETTI F S,EBERLI G P.The velocity-deviation log:a tool to predict pore type and permeability trends in carbonate drill holes from sonic and porosity or density logs[J].AAPG Bulletin,1999,83(3):450-466

[17]许敏.双孔隙度测井评价低孔白云岩干气藏[J].测井技术,1991,15(3):153-157

XU M.Evaluation of low porosity dry gas dolomite reservoir using dual porosity logs[J].Well Logging Technology,1991,15(3):153-157

[18]谭廷栋.中子和密度测井找气的一种特殊解释方法[J].石油学报,1992,13(4):31-40

TAN T D.A special interpretation method for gas finding by neutron and density log[J].Acta Petrolei Sinica,1992,13(4):31-40

[19]IJASAN O,TORRES-VERDN C,PREEG W E.Interpretation of porosity and fluid constituents from well logs using an interactive neutron-density matrix scale[J].Interpretation,2013,1(2):T143-T155

[20]XU S,PAYNE M A.Modeling elastic properties in carbonate rocks[J].The Leading Edge,2009,28(1):66-74

[21]WANG Z,WANG R,WEGER R J,et al.Pore-scale modeling of elastic wave propagation in carbonate rocks[J].Geophysics,2015,80(1):D51-D63

[22]蔡涵鹏,贺振华,唐湘蓉,等.碳酸盐岩孔隙结构影响分析和等效孔隙结构参数计算[J].石油物探,2013,52(6):566-572

CAI H P,HE Z H,TANG X R,et al.Influence analysis of carbonate pore structure and calculation of equivalent pore structure parameters[J].Geophysical Prospecting for Petroleum,2013,52(6):566-572

[23]WU T T.The effect of inclusion shape on the elastic moduli of a two-phase material[J].International Journal of Solids and Structures,1966,2(1):1-8

[24]MAVKO G,MUKERJI T,DVORKIN J.The rock physics handbook:tools for seismic analysis of porous media[M].New York:Cambridge University Press,2009:129-132

[25]NORRIS A N.A differential scheme for the effective moduli of composites[J].Mechanics of materials,1985,4(1):1-16

[26]ZIMMERMAN R W.Elastic moduli of a solid containing spherical inclusions[J].Mechanics of Materials,1991,12(1):17-24

[27]BERRYMAN J G,BERGE P A.Critique of two explicit schemes for estimating elastic properties of multiphase composites[J].Mechanics of Materials,1996,22(2):149-164

[28]RUIZ F,DVORKIN J.Sediment with porous grains:rock-physics model and application to marine carbonate and opal[J].Geophysics,2009,74(1):E1-E15

[29]RUIZ F,DVORKIN J.Predicting elasticity in nonclastic rocks with a differential effective medium model[J].Geophysics,2010,75(1):E41-E53

[30]FOURNIER F,LEONIDE P,BISCARRAT K,et al.Elastic properties of microporous cemented grainstones[J].Geophysics,2011,76(6):E211-E226

[31]SUN Z D,WANG H Y,LIU Z Z,et al.The theory and application of DEM-Gassmann rock physics model for complex carbonate reservoirs[J].The Leading Edge,2012,31(2):152-158

[32]RUIZ F,DVORKIN J.Empirical and theoretical models:applicability to predictions of elastic moduli of composites and rocks[J].The 42ndUS Rock Mechanics Symposium,2008:112-120

[33]JOHANSEN T A,DROTTNINGÅ,LECOMTE I,et al.An approach to combined rock physics and seismic modelling of fluid substitution effects[J].Geophysical Prospecting,2002,50(2):119-137

[34]BERRYMAN J G,PRIDE S R,WANG H F.A differential scheme for elastic properties of rocks with dry or saturated cracks[J].Geophysical Journal International,2002,151(2):597-611

[35]LI H B,ZHANG J J.Modulus ratio of dry rock based on differential effective-medium theory[J].

Geophysics,2010,75(2):N43-N50

[36]LI H B,ZHANG J J.Elastic moduli of dry rocks containing spheroidal pores based on differential effective medium theory[J].Journal of Applied Geophysics,2011,75(4):671-678

[37]LI H B,ZHANG J J.Analytical approximations of bulk and shear moduli for dry rock based on the differential effective medium theory[J].Geophysical Prospecting,2012,60(2):281-292

[38]李宏兵,张佳佳,姚逢昌.岩石的等效孔隙纵横比反演及其应用[J].地球物理学报,2013,56(2):43-51

LI H B,ZHANG J J,YAO F C.Inversion of effective pore aspect ratios for porous rocks and its applications[J].Chinese Journal of Geophysics,2013,56(2):43-51

[39]李宏兵,张佳佳.多重孔岩石微分等效介质模型及其干燥情形下的解析近似式[J].地球物理学报,2014,57(10):3422-3430

LI H B,ZHANG J J.A differential effective medium model of multiple-porosity rock and its analytical approximations for dry rock[J].Chinese Journal of Geophysics,2014,57(10):3422-3430

[40]LUCIA F J.Carbonate reservoir characterization:an integrated approach[M].Berlin:Springer Science & Business Media,2007:75-81

[41]钱恪然,张峰,李向阳,等.基于网格分析法的页岩储层等效孔隙纵横比反演[J].石油物探,2015,54(6):724-734

QIAN K R,ZHANG F,LI X Y,et al.Inversion of effective pore aspect ratio for shale reservoir using grid search method[J].Geophysical Prospecting for Petroleum,2015,54(6):724-734

[42]赵文智,沈安江,周进高,等.礁滩储集层类型、特征、成因及勘探意义:以塔里木和四川盆地为例[J].石油勘探与开发,2014,41(3):257-267

ZHAO W Z,SHEN A J,ZHOU J G,et al.Types,characteristics,origin and exploration significance of reef-shoal reservoirs:a case study of Tarim Basin,NW China and Sichuan Basin,SW China[J].Petroleum Exploration and Development,2014,41(3):257-267

[43]邹才能,杜金虎,徐春春,等.四川盆地震旦系—寒武系特大型气田形成分布、资源潜力及勘探发现[J].石油勘探与开发,2014,41(3):278-293

ZOU C N,DU J H,XU C C,et al.Formation,distribution,resource potential and discovery of the Sinian-Cambrian giant gas field,Sichuan Basin,SW China[J].Petroleum Exploration and Development,2014,41(3):278-293

(编辑：朱文杰)

Four parameters porosity inversion method representing the effect of pore morphology

GUO Jiliang,LI Hongbing,LI Ming,ZHANG Yan,LI Jinsong,YU Hao,LIU Xiaohong

(ResearchInstituteofPetroleumExploration&Development,PetroChina,Beijing100083,China)

Abstract: The deviations arise when inverting the porosity of reservoirs in complex pore structure with conventional porosity inversion methods.The effect of pore morphology on acoustic velocity can be indicated quantitatively by means of the equivalent media model.S-wave velocity is introduced to improve porosity equation and to calculate the effects of porosity and pore aspect ratio.The porosity and pore aspect ratio are simultaneously inverted using the density,neutron porosity,acoustic velocity and S-wave velocity data to improve inversion accuracy.Firstly,the initial porosity is inverted with neutron porosity,density and acoustic velocity,and the initial pore aspect ratio is calculated by difference equivalent model (DEM).Then,the acoustic porosity and pore aspect ratio are inverted simultaneously with bulk density and velocities information.Finally,the formation porosity and pore aspect ratio are inverted simultaneously with the comprehensive utilization of neutron porosity,S-wave velocity,acoustic velocity and bulk density.This method is applied to invert the porosity of deep dolomite formation in somewhere southwest of China.By comparing the results with other methods,the validity of this four parameter porosity inversion method is proved.

pore aspect ratio,porosity,difference equivalent model (DEM),four parameter porosity inversion,simultaneous inversion

2015-11-23;改回日期：2016-02-18。

郭继亮(1983—),男,博士,研究方向为地震岩石物理建模和岩石物理反演。

国家自然科学基金青年基金项目“基于波动方程理论的储层弹性参数反演及多尺度表征”(41504110)资助。

P631

A

1000-1441(2016)04-0576-11DOI:10.3969/j.issn.1000-1441.2016.04.013

This research is financially supported by the National Natural Science Foundation of China (Grant No.41504110).