基于Holtan产流的分布式水文模型

包红军,王莉莉,李致家,姚　成

(1. 国家气象中心,北京　100081; 2. 河海大学水文水资源学院,江苏 南京　210098)



基于Holtan产流的分布式水文模型

包红军1,王莉莉1,李致家2,姚成2

(1. 国家气象中心,北京100081; 2. 河海大学水文水资源学院,江苏 南京210098)

基于GIS与DEM技术,构建基于Holtan产流的分布式水文模型(Grid-Holtan模型)。模型以栅格为计算单元,栅格产流采用基于Holtan下渗方法的超渗产流计算,坡面汇流和河道汇流均采用逐栅格的一维扩散波水流演算模型模拟。将Grid-Holtan模型、陕北模型与新安江模型应用于半干旱的沁河孔家坡流域。结果表明,Grid-Holtan模型、陕北模型的模拟效果好于新安江模型,Grid-Holtan模型洪峰模拟效果更好。

水文过程模拟;分布式水文模型;Grid-Holtan模型;陕北模型;新安江模型;Holtan产流;一维扩散波;沁河孔家坡流域

水文过程的非线性与相互间作用,导致水文现象具有高度时空变异性[1]。流域下垫面的空间差异性分布特征成为影响流域降雨-径流预报精度的重要因素。随着现代地理信息系统(GIS)技术、数字高程模型(DEM)技术、遥感(RS)技术的快速发展,分布式水文模型以能够借助GIS技术、遥感与遥测等空间信息描述水文过程的机理与模拟流域的降雨-径流响应[2-3],与雷达、卫星估测降水[4]、数值天气预报降水[5-7]结合进行洪水预报,延长洪水预报预见期,成为水文模型的发展趋势与研究前沿[8-9]。

目前,基于水文循环的动力学机制的分布式水文物理模型由于模型输入与参数化方案的复杂性、计算资源消耗大,在流域洪水模拟与预报中应用较少,并且模型模拟与预报精度往往不高[8]。而且,任何一个分布式水文模型都只是在一定程度上反映了流域内的空间多样性与水文过程的物理机制,物理性模型只是相对于概念性模型而言,并没有“完全”的分布式物理模型。考虑到洪水模拟与预报特点,以及概念性模型的简单高效,国内外学者开始在分布式水文模型中融入概念性模型的优点,构建用于洪水预报的概念性与物理性相结合的分布式水文模型。美国天气局水文办公室(Office of Hydrologic development, National Weather Service,National Oceanic and Atmospheric Administration)组织的distributed model intercomparsion project(DMIP)项目研究结论也支持这一观点,并指出[10]:率定过的分布式水文模型洪水预报效果优于或者至少相当于集总式水文模型;用于洪水预报的分布式水文模型,应采用概念性的降雨径流模型与基于物理机制的分布式汇流模型。概念性降雨-径流模型是在大量的野外试验基础上建立起来的,符合水文过程的内在客观物理规律,具有一定的物理基础,并且结构简单、输入项少,易进行模型率定,常常可以获得较高的降雨-径流模拟与预报精度。概念性降雨-径流模型都经过了大量的实例验证,积累了丰富的应用经验,在此基础上进一步融入分布式手段加强对降雨、地貌特征、土壤类型和植被覆盖等因素空间变异性的描述,可以集两者之所长,促进分布式水文模型的进一步发展[8]。HL-RMS模型[11]、TOPKAPI模型[12]、BTOPMC模型[13]、Grid-Xinanjiang模型[14-15]等分布式水文模型都属于此类模型,其描述的产流机制大都反映的是蓄满产流[12-15],适用于我国的湿润与半湿润地区洪水模拟与预报。在我国北方半干旱与干旱地区,流域产流中还存在较大比例的超渗产流。为了提高在干旱半干旱流域的洪水模拟与预报能力,本文结合GIS、RS和DEM技术,以DEM栅格为流域计算单元,根据超渗产流理论,每个计算单元内产流计算采用概念性的Holtan下渗模型;考虑栅格之间的水量交换以及河道排水网络的影响,采用逐栅格的一维扩散波模型进行流域坡面与河道的分布式汇流,形成分布式水文模型(Grid-Holtan模型)。将该模型、陕北模型以及新安江模型应用于半干旱地区沁河孔家坡站以上流域水文过程模拟并对比分析研究,以探讨模型的洪水模拟与预报性能。

1　Grid-Holtan模型

Grid-Holtan模型将每个栅格作为一个计算单元处理,同一栅格内假设空间分布均匀,只考虑水文要素在栅格间的变化。模型通过计算出每个栅格垂直方向上的蒸散发、产流量,得到逐个栅格的产流量。栅格汇流演算时,考虑河道栅格与坡面栅格2种类型,若为河道栅格,则其地表径流和地下径流按比例汇入。模型的坡面汇流与河道汇流均采用逐栅格的一维扩散波水流演算法,这样就可以得到整个流域出口断面的水文过程。

1.1产流模型

1.1.1植被冠层截留计算

不同下垫面土地覆盖类型对植被冠层截留的降水量有明显差别,分布式水文模型考虑了流域下垫面土地覆盖的空间变化,体现分布式模型的优势。本研究的植被冠层截留计算采用文献[16]提出的方法:利用美国地质调查局提供的30″×30″下垫面流域17类土地覆盖数据,简化为林地、草地、耕地与水面,通过建立土壤覆盖类型与参数植被最大截留量Sr max之间的关系,可以得到每个栅格的Sr max。进入土壤的净雨量Pei(t)由式(1)计算:

(1)

式中Pi(t)——单元栅格i上t时刻的降雨量;Sri(t)——单元栅格i上t时刻的植被截留缺水量。

1.1.2河道降水处理

河道降水指的是直接降落到实际流域河道里、不参加坡面产汇流计算的降水量。在分布式水文模型进行洪水模拟与预报中,如不考虑河道降水往往会导致洪水预报的峰值偏小、峰现时间滞后,影响流域出口控制断面的洪水过程,尤其在河网密度较发达地区或当降雨强度较大时,河道降水的影响更不能忽视。在Grid-Holtan模型中,增加了对河道降水的考虑,把河道降水直接与河道栅格产流量叠加进行基于一维扩散波演算模型的河道水流演算。

单元栅格河道降水可表示为

(2)

式中:Pc——时段内栅格内非河道植被冠层截留量,mm;Lc——河道长度,m;Wc——河道断面最大过水面积所对应的水面宽,m;Ac——栅格单元的面积,m2;P——时段降雨量,mm。

1.1.3蒸散发计算

与湿润半湿润流域相比,干旱半干旱流域表层土壤较薄,缺水量较大,流域植被覆盖相对较少,因此Grid-Holtan模型中考虑植被及根系截留层蒸散发量Eai(t)和土壤层蒸散发量Ebi(t)。Eai(t)可由式(3)计算[16]:

(3)

式中:Epi(t)——单元栅格i上t时段的蒸散发能力;ρ——植被及根系截留层蒸散发控制指数。

Ebi(t)可由式(4)计算:

(4)

式中:Suz i(t)——单元栅格i上t时段的土壤层蓄水量;Di(t)——单元栅格i上t时段的土壤层缺水量;υ——土壤层蒸散发控制指数。

1.1.4Holtan产流计算

模型产流结构中,下渗过程是流域降雨径流过程的重要组成部分,决定了流域坡面流的形成。本文选取Holtan下渗模型:

(5)

式中:f——下渗率;FP——土壤根系层的蓄水能力,相当于田间持水量;θ——土壤层蓄水量;fc——稳定下渗率;D——土壤根系层的蓄水能力与土壤层蓄水量之差,α、δ——Holtan下渗模型待求的系数。

单元栅格i上t时段内地表产流量RSi的计算式如下:

(6)

(7)

本文对地下产流量RIi的计算主要是基于基流的考虑[17]:

(8)

式中:R0i——t=0时单元栅格i上的平均径流量;a、m——常数。

对于非河道栅格,栅格产流量由地表径流与地下径流组成;对于河道栅格,栅格产流量主要由地表径流、地下径流以及栅格河道降水组成。

1.2一维扩散波汇流模型

Grid-Holtan模型采用一维扩散波水流演算模型进行逐栅格分布式汇流计算。对于坡面栅格,假定其存在一个“虚拟河道”,地表径流与地下径流汇入虚拟河道进行河道水流演算;对于含河道栅格,地表径流、地下径流与河道降水汇入河道进行水流演算。水流演算采用一维扩散波模型。

1.2.1坡面汇流

Grid-Holtan模型的坡面水流运动利用一维扩散波方程组来描述:

(9)

式中:hs——坡面水流的水深,m;t——时间,s;us——坡面水流的平均流速,m/s;qs——单位时间内所计算的坡面径流深,m/s;x——流径长度,m;So——沿出流方向的地表坡度;Sf——沿出流方向的地表摩阻比降。

在进行栅格间汇流演算时,式(9)需要在每个栅格单元上进行离散,其中的连续性方程为

(10)

式中:Qsup——上游栅格入流量,m3/s;Qs——栅格单元的地表径流流量,m3/s;Qsout——栅格单元的地表径流出流量,m3/s。

本研究对扩散波方程组的求解采用Preissmann隐式差分格式[18]。

1.2.2河道汇流

河道水流运动的一维扩散波方程组为

(11)

式中:Ach——河道断面的过水面积,m2;Qch——河道流量,m3/s;ql——单宽旁侧入流,m2/s;hch——河道水流深度,m;Soc——河道坡度;Sfc——河道摩阻比降。

同样,对于湍流而言,有[19-20]:

其中

式中:nc——河道的曼宁糙率系数;R——水力半径,m;χ——湿周,m。

2　模 型 应 用

2.1流域介绍

选取黄河一级支流沁河流域的孔家坡水文站控制流域作为模型应用验证流域。沁河流域位于黄河流域中游,是黄河三花间的两大支流之一,发源于山西省沁源县,干流河道全长485 km,地域横跨山西、河南两省,其中山西境内流域面积为12 304 km2,占沁河流域面积90%。流域内年降水分布不均,主要在6—9月,占全年降水量的68%左右,降水量年际变化大,属于半干旱流域。孔家坡流域位于山西省境内,流域面积1 454 km2,流域内含有孔家坡水文站、赤石桥雨量站和郭道雨量站,该流域属于受人类活动影响较小的自然流域。

沁河流域历史上发生过多次大洪水。历史调查最大洪水洪峰流量为14 000 m3/s,1949年中华人民共和国建立以来的最大洪水出现在1982年,下游武陟站洪峰流域达到4 130 m3/s。沁河流域约占小花间无工程控制区面积的一半左右,对黄河干流防洪有一定的影响。本研究所选的孔家坡流域1958—2001年间发生10次洪水,其中1993年的洪水最大,洪峰流量达到2 070 m3/s。

2.2主要数据及来源

本研究Grid-Holtan模型使用的水文数据摘自《中华人民共和国水文年鉴：山西省沁河水文资料(1958—2001年)》,DEM数据来自于美国地质调查局(USGS)提供的全球30″×30″分辨率的DEM数据[22](图1),提取孔家坡流域水系(图2,提取阈值为30 km2)。流域下垫面覆盖数据采用美国地质调查局提供的全球30″×30″土地覆盖数据[23]。

图1　基于DEM的流域单元栅格流向Fig. 1　Flow direction in grid cells in Kongjiapo Catchment based on DEM

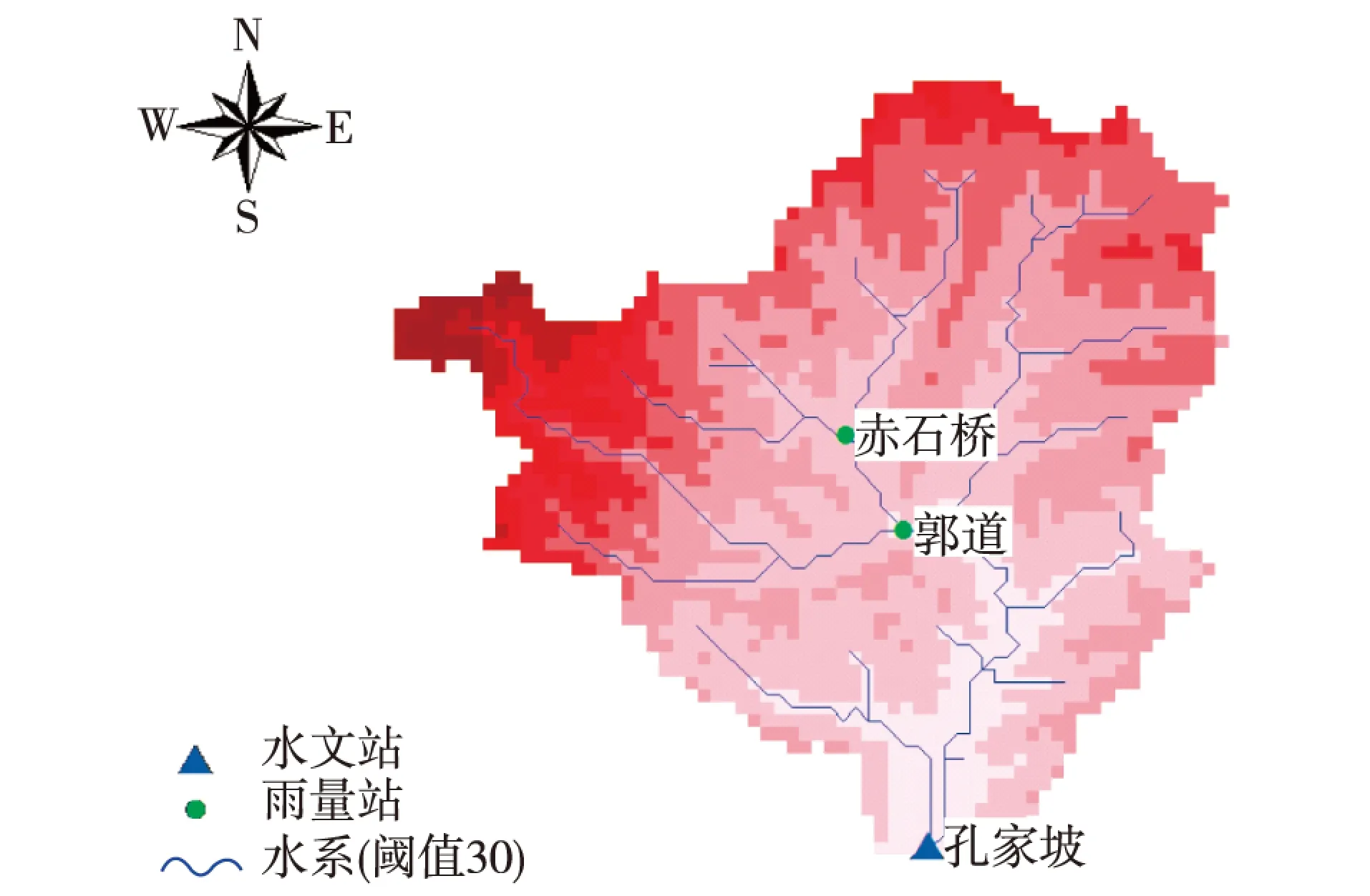
图2　孔家坡流域水系概化Fig. 2　Sketch of river system in Kongjiapo Catchment

2.3模型参数

Grid-Holtan模型中,共有7个参数。本研究在沁河孔家坡流域参数的取值范围如下:Srmax=0.02(林地)、0.01(耕地)、0.01(草地),ρ=2.0,υ=1.0,Holtan下渗系数α=0.51,δ=0.36,fc=8.6,nc=0.1(林地)、0.035(耕地)、0.17(草地)。

2.4模型应用与分析

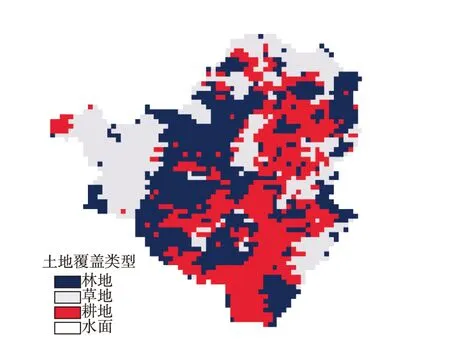
图3　孔家坡流域下垫面覆盖情况Fig. 3　Land cover types of Kongjiapo Catchment

选取1958—2001年间10场孔家坡流域汛期的典型洪水,时间步长取为1 h,用Grid-Holtan模型、陕北模型、新安江模型等3个模型对其进行洪水模拟,其中前7场洪水数据用来率定模型参数,后3场洪水数据用来检验模型。根据本研究使用的DEM与下垫面覆盖数据的分辨率(30″×30″),孔家坡流域划分为2 309个30″×30″的网格计算单元(图1),流域降水资料采用反距离权重法插值到网格计算单元。Grid-Holtan模型的产流参数主要通过流域出口断面的流量过程来率定,因此模型产流参数在全流域采用的同一套参数,其参数率定主要采用基于参数物理意义的人工率定方法。Sr max根据美国地质调查局提供的全球30″×30″土地覆盖数据得到的4种下垫面覆盖(林地、水面、耕地、草地)分别率定,扩散波汇流模型采用分布式参数,即每个栅格汇流糙率nc根据文献[24]提供的根据美国地质调查局提供的全球30″×30″土地覆盖数据得到的4种下垫面覆盖(林地、水面、耕地、草地)糙率取值方推求(孔家坡流域下垫面土地覆盖分布情况见图3)。流域初始状态初值根据新安江模型日模型结果推求。产流参数率定结果为:ρ=2.0,υ=1.0,fc=8.6 mm/h,α=0.51,δ=0.36。表1为3个模型次洪模拟结果特征值。从表1可以看出:Grid-Holtan模型与陕北模型模拟精度相近,效果较好,新安江模型模拟效果较差;Grid-Holtan模型在洪峰误差控制和径流深误差控制上好于其他模型,这也证明了Grid-Holtan模型理论与应用的合理性和可靠性。

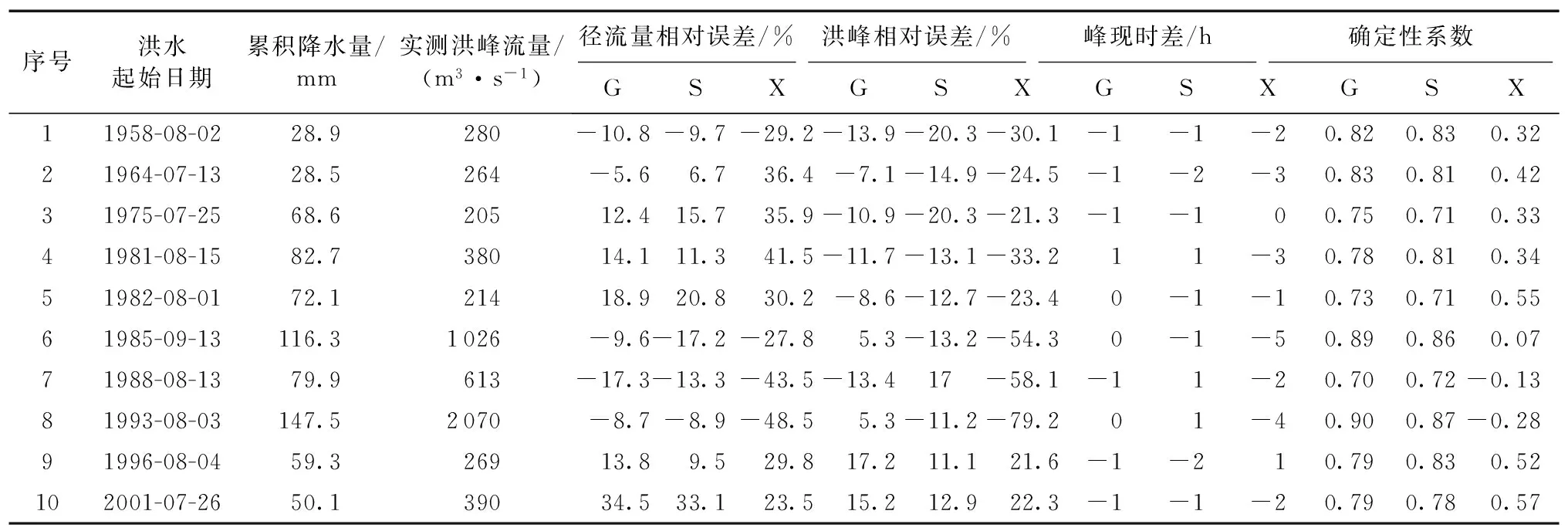
表1　3个水文模型在孔家坡流域洪水模拟特征值对比Table 1　Comparison of simulated results of flood in Kongjiapo Catchment using three hydrological models

注:G代表Grid-Holtan模型, S代表陕北模型,X代表新安江模型。

经过分析可以看出3个水文模型在孔家坡流域洪水模拟中的优劣,总结如下:(a)从洪峰来看,Grid-Holtan模型与陕北模型在10场洪水模拟上效果明显好于新安江模型。Grid-Holtan模型的洪峰相对误差平均值达到10.9%,陕北模型的洪峰相对误差平均值达到14.7%,而新安江模型的洪峰相对误差平均值为36.3%,这也证明了流域中存在一定比例的超渗产流,基于蓄满产流的新安江模型在流域的洪峰模拟上效果较差,满足不了洪水预报的要求。(b)从洪量来看,Grid-Holtan模型与陕北模型模拟效果基本相同,洪量相对误差平均值均为14.6%,说明Grid-Holtan模型的合理性。(c)从峰现时间及过程线拟合程度上来看,Grid-Holtan模型模拟误差明显好于陕北模型与新安江模型,这充分体现出分布式水文模型的优点,即在产汇流中考虑到半湿润地区下垫面空间分布的不均匀性。(d)10场洪水,2001年的洪水模拟中,Grid-Holtan模型和陕北模型模拟效果均不好,径流量误差分别达到34.5%和33.1%。究其原因,一方面半干旱流域产汇流机理比较复杂,目前国内外也难有完备的理论体系和成熟的洪水预报模型[25],本研究是基于相对比较简单的Holtan产流模型,还有进一步改进的空间;另一方面本研究由于资料原因,所选的洪水样本只有10场,相对较少,据此率定出来参数的普适性还需要进一步提升。另外,研究半干旱流域产汇流时,计算时间步长一般要小于或等于30 min,本研究由于资料原因计算时间步长取为1 h,对于超渗产流稍显较大,也是影响洪水模拟精度的原因之一。

Grid-Holtan模型和陕北模型在半干旱孔家坡流域均取得较为理想的模拟效果,相比而言,Grid-Holtan模型在洪峰误差控制上效果更好一些,主要原因是Grid-Holtan模型充分考虑到了半干旱地区下垫面的空间变异性和半干旱流域存在一定的超渗产流。其次,半湿润半干旱的洪水过程多为暴涨暴落。研究结果表明：Grid-Holtan模型退水较快,原因在于孔家坡流域存在一定的地下水,这是模型需要进一步完善的地方。新安江模型虽然在洪水整体模拟上效果不好,但在退水过程表现较好,这是因为新安江模型是三水源模型,模型考虑了地下水。要提高新安江模型在半干旱流域的模拟精度,可改进模型的产流方案,如增加超渗产流的新安江模型[16]。

3　结　　语

本研究针对半干旱地区的产汇流特性,结合GIS、RS和DEM技术,在Holtan产流理论的基础上以DEM栅格为流域计算单元,并考虑栅格之间的水量交换以及河道排水网络的影响,采用一维扩散波模型进行汇流计算,形成基于Holtan产流的栅格型分布式水文模型(Grid-Holtan模型)。通过Grid-Holtan模型、陕北模型、新安江模型在半干旱孔家坡流域应用来看,将该水文模型与陕北模型应用于半干旱地区沁河孔家坡站以上流域水文过程模拟并对比分析,结果表明Grid-Holtan模型与陕北模型均能取得较高的模拟精度,新安江模型模拟精度较差。笔者认为,针对半干旱及干旱流域水文过程的复杂性,仍存在需要进一步的研究:

a. Grid-Holtan模型是基于概念性产流模型与分布式汇流模型的栅格型超渗产流水文模型,其对于半干旱流域的陡涨陡落洪水过程,特别是洪水模拟精度较好。但与新安江模型相比,在洪水退水过程模拟不理想,这是因为三水源新安江模型较好地考虑了流域的地下水过程,而Grid-Holtan模型缺少对地下水过程的完备考虑。另外,Grid-Holtan模型产流机制是单一的超渗产流,在我国半湿润半干旱地区大部分都是蓄满与超渗共存,模型中还应该加入蓄满产流模块,采用蓄满超渗混合产流方式改进模型产流方案,如先蓄满后超渗模型、先超渗后蓄满模型以及在新安江模型蓄满产流基础上增加超渗产流的产流模型[26-27],这样才能与实际情况更相符,特别是在新安江模型蓄满产流基础上增加超渗产流的产流模型,可以弥补Grid-Holtan模型在流域地下水过程模拟的缺陷。

b. 近年来,由于气候变化和人类活动的双重作用改变了流域下垫面水文产汇流特性,特别是流域对洪水的调蓄能力会有一定的变化,这对流域水文模型的率定与检验提出新的考验。已经有研究表明,在我国北方流域下垫面变化对洪峰影响比对径流深的影响要大[28]。因此,如何在分布式水文模型的构建与验证中综合考虑下垫面变化的影响,是模型下一步应用发展要解决的问题。

[1] NRC. Opportunities in the hydrologic sciences[M]. Washington D. C.:National Academy Press, 1991.

[2] VIEUX B E. Distributed hydrologic modeling using GIS[M]. Dordrecht, the Netherlands: Kluwer Academic Publishers,2001.

[3] ABBOTT M B， REFSGAARD J C. Distributed hydrological modelling[M]. Dordrecht, the Netherlands: Kluwer Academic Publishers, 1996.

[4] LI,Zhijia,GE Wenzhong, LIU Jintao, et al. Coupling between weather radar rainfall data and a distributed hydrological model for real-time flood forecasting[J]. Hydrological Sciences Journal, 2005, 49(6): 945-958.

[5] CLOKE H L, PAPPENBERGER F. Ensemble flood forecasting: a review[J]. Journal of Hydrology,2009, 375: 613-626.

[6] 包红军,赵琳娜. 基于集合预报的淮河流域洪水预报研究[J], 水利学报, 2012,43(2):216-224.(BAO Hongjun,ZHAO Linna. Flood forecast of Huaihe River based on TIGGE ensemble oredictions[J]. Journal of Hydraulic Engineering,2012,43(2):216-224. (in Chinese))

[7] BAO Hongjun, ZHAO Linna. Development and application of an atmospheric-hydrologic-hydraulic flood forecasting model driven by TIGGE ensemble forecasts[J]. Acta Meteor Sinica,2012,26(1), 93-102.

[8] 张金存,芮孝芳.分布式水文模型构建理论与方法评述[J].水科学进展,2007,18(2):286-292.(ZHANG Jincun,RUI Xiaofang. Discussion of theory and methods for building a distributed hydrologic model[J]. Advances in Water Science,2007,18(2):286-292. (in Chinese))

[9] 杨大文,李忡,倪广恒,等.分布式水文模型在黄河流域的应用[J].地理学报,2004,59(1):143-154.(YANG Dawen, LI Chong, NI Guangheng,et al. Application of a distributed hydrological model to the yellow river basin[J]. Acta Geographica Sinica,2004,59(1):143-154. (in Chinese))

[10] MICHAEL S,SEO D J,KOREN V. The distributed model intercomparson project(DMIP): motivation and experiment design[J]. Journal of Hydrology,2004,298(1/2/3/4):4-26.

[11] KOREN V, SEANN R, MICHAEL S, et al. Hydrology laboratory research modeling system (HL-RMS) of the US national weather service[J]. Journal of Hydrology,2004, 298:297-318.

[12] TODINI E, CIARAPICA L. The TOPKAPI model[C]//SINGH V P, FREVERT D K. Mathematical Models of Large Watershed Hydrology. Littleton: Water Resources Publications, LLC, 2001.

[13] BAO Hongjun, WANG Lili, LI Zhijia, et al. Hydrological daily rainfall-runoff simulation with BTOPMC model and comparison with Xin’anjiang model[J]. Water Science and Engineering, 2010,3(2):121-131.

[14] 姚成,纪益秋,李致家,等.栅格型新安江模型的参数估计及应用[J].河海大学学报(自然科学版),2012,40 (1): 42-47.(YAO Cheng, JI Yiqiu, LI Zhijia, et al. Parameter estimation and application of grid-based Xin’anjiang model[J]. Journal of Hohai University (Natural Sciences),2012,40(1):42-47. (in Chinese))

[15] YAO Cheng, LI, Zhijia, YU, Zhongbo, et al. A priori parameter estimates for a distributed, grid-based xinanjiang model using geographically based information[J]. Journal of Hydrology, 2012,468/469(6):47-62.

[16] 王莉莉,李致家,包红军.基于栅格的分布式超渗产流水文模型构建及比较[J].河海大学学报(自然科学版),2010,38(2):123-128.(WANG Lili, LI Zhijia, BAO Hongjun. Development and comparison of grid-based distributed hydrological models for excess-infiltration runoffs[J]. Journal of Hohai University (Natural Sciences), 2010,38(2):123-128. (in Chinese))

[17] HORTON R E. The role of infiltration in the hydrologic cycle[J]. Eos Transactions American Geophysical Union, 1933, 14(1):143-154.

[18] 包红军.基于EPS的水文与水力学相结合的洪水预报研究[D].南京:河海大学, 2009.

[19] JULIEN P Y, SAGHAFIAN B. CASC2D users manual: a two dimensional watershed rainfall-runoff model(civil engineering report, CER90-91PYJ-BS-12)[R]. Fort Collins:Colorado State University, 1991.

[20] 姚成.基于栅格的新安江(Grid-Xinanjiang)模型研究[D]. 南京:河海大学, 2009.

[21] 中华人民共和国水利部水文局.中华人民共和国水文年鉴 ：山西省沁河水文资料(1958—2001年)[R].北京:中华人民共和国水利部水文局,2002.

[22] U.S. Geological Survey (USGS). GTOP30[EB/OL].[2006-02-10].http://edc.usgs.gov/products/elevation/gtopo30.html,2005.

[23] U.S. Geological Survey (USGS). Global Land Cover Characteristics Data Base[EB.OL]. [2006-02-10]. http://edcdaae.usgs.gov/globodc2_.asp,2005.

[24] 王莉莉,陈德辉.基于栅格的二维分布式超渗产流水文模型[J].水电能源科学,2011,29(11):6-10,54.(WANG Lili, CHEN Dehui. Two-dimensional distributed runoff yield hydrologic model based on grid[J]. Water Resource and Power, 2011,29(11):6-10,54. (in Chinese))

[25] WHEATER H, SOROOSHIAN S, SHARMA K D. Hydrological modelling in arid and semi-arid areas[M]. Cambridge,Singapore: Cambridge University Press,2007.

[26] 李致家, 黄鹏年, 姚成,等. 灵活架构水文模型在不同产流区的应用[J]. 水科学进展,2014,25(1):28-35.(LI Zhijia, HUANG Pengnian,YAO Cheng, et al. Application of flexible-structure hydrological models in defferent runoff generation regions[J]. Advances in Water Science,2014,25(1):28-35.(in Chinese))

[27] 王贵作,任立良.基于栅格垂向混合产流机制的分布式水文模型[J]. 河海大学学报(自然科学版), 2009, 37(4):386-390.(WANG Guizuo, REN Liliang. Distributed hydrological model based on grid vertically-mixed runoff generation[J]. Journal of Hohai University (Natural Sciences), 2009, 37(4):386-390. (in Chinese))

[28] 李致家,周赛,姚玉梅,等.经验方法研究下垫面变化对洪水的影响[J].湖泊科学, 2012,24(4):637-642.(LI Zhijia, ZHOU Sai,YAO Yumei, et al. Impacts of altered basin landscape on floods using an empirical method[J]. Journal of Lake Sciences,2012,24(4):637-642. (in Chinese))

A distributed hydrological model based on Holtan runoff generation theory

BAO Hongjun1, WANG Lili1, LI Zhijia2, YAO Cheng2

(1.NationalMeteorologicalCenter,ChinaMeteorologicalAdministration,Beijing100081,China;2.CollegeofHydrologyandWaterRecourses,HohaiUniversity,Nanjing210098,China)

Using the GIS and DEM techniques, a distributed hydrological model based on a runoff generation theory (the Grid-Holtan model) was developed. For each computational cell, the infiltration-excess runoff was calculated with the Holtan infiltration method, and the overland flow and river flow routing were simulated with the one-dimensional diffusion wave model. The Grid-Holtan model, Shanbei model, and Xinanjiang model were applied to the Kongjiapo Catchment of the Qinhe Basin, in China. The results show that the Grid-Holtan model and Shanbei model perform better in flood simulation than the Xinanjiang model, while the flood peak simulation accuracy of the Grid-Holtan model is higher.

hydrological process simulation; distributed hydrological model; Grid-Holtan model; Shanbei model; Xinanjiang model; Holtan runoff generation model; one-dimensional diffusion wave; Kongjiapo Catchment of Qinhe Basin

1000-1980(2016)04-0340-07

10.3876/j.issn.1000-1980.2016.04.010

2015-11-23

国家自然科学基金(51509043,41130639); 国家气象中心水文气象预报团队和中国气象局首批青年英才计划(2014-2017)

包红军(1980—),男，江苏淮阴人,高级工程师,博士,主要从事水文气象预报、流域水文模型及洪水预报预警研究。E-mail:baohongjun@cma.gov.cn

P338

A