降雨空间分布的模糊熵聚类分析

张继国,管耀宗,朱永忠

(1. 河海大学水利信息统计与管理研究所,江苏 常州　213022; 2. 河海大学理学院,江苏 南京　210098)



降雨空间分布的模糊熵聚类分析

张继国1,管耀宗2,朱永忠2

(1. 河海大学水利信息统计与管理研究所,江苏 常州213022; 2. 河海大学理学院,江苏 南京210098)

为了提高降雨量插值精度,充分挖掘降雨变量信息,利用模糊熵聚类分析算法,对流域内雨量站进行模糊熵聚类研究,通过基于可能性分布和距离判定的聚类有效性函数确定模糊熵系数和聚类数,从而得到模糊聚类结果,改进原有的插值方法。以淮河流域蚌埠站以上区域99个雨量站雨量数据,分别在一般情况下和模糊熵聚类情况下做交叉验证,结果显示,模糊熵聚类分析在反距离平方插值法中对降雨精度有所提升。

降雨空间分布;降雨数据精度;模糊熵聚类分析;聚类有效性分析;降雨量插值

HohaiUniversity,Changzhou213022,China;2.CollegeofSciences,HohaiUniversity,Nanjing210098,China)

降雨量是水文模型中径流模拟最基本、最主要的一个输入项,是研究其他水文问题的基础。其空间分布特征是影响产汇流模拟及其他一系列水文问题的重要控制因素[1]。随着研究的深入,水文模型对降雨数据精度和广度的要求越来越高。理论上获取高精度降雨数据的方法是建立高密度的雨量站网,但是由于经济条件和技术手段的约束,大部分地区气象观测站点数量不足,分布密度有限。因此,利用现有气象观测站的数据,通过空间插值对观测数据进行补充尤为重要,孔云峰等[2]通过多种插值方法探究了美国德州的空间雨量数据。然而,大尺度流域上的降雨空间具有很强的时空分布不均匀性和复杂性,对此,在区域内对已有站点作聚类分区处理,即将复杂的降雨测量站点系统划分成不同的子系统,减少不确定性因素的影响,是一种切实有效的研究方法[3]。李生辰等[4]在2007年研究了青藏高原降雨分区问题。杨绚等[5]在2008年通过降雨变化特征对中国干旱地区进行了聚类划分;郑永宏等[6]2012年研究了湖北省的降雨分区问题。

聚类分区主要分硬聚类和模糊聚类。相对于硬聚类,模糊聚类方法能够对类与类之间有交叉的数据样本集进行有效的聚类,所得的聚类结果明显优于硬聚类方法。由于模糊聚类建立了数据样本对于类别的不确定性的描述,表达了样本类属的模糊性,因此能够更客观地反映实际情况[7],并被广泛应用于水文研究中[8-9]。本文根据模糊熵聚类算法,将淮河流域蚌埠站以上的99个雨量站进行模糊划分,并研究模糊聚类分析在降雨量插值精度中的应用,为流域内雨量建模分析、水文循环研究、灾害预报等提供理论依据。

1　模糊熵聚类

1.1模糊熵目标函数

Tran等提出的模糊熵聚类算法(fuzzy entropy clustering)[10]是在模糊C均值聚类算法(fuzzyC-means clustering)基础上,引入熵的概念,对隶属度值分布进行了算法优化。

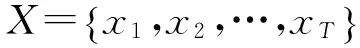
(1)

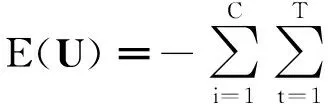
(2)

式中:C——聚类数;T——样本数;uit——成员xt对聚类Ci的隶属度;n——模糊熵系数;θi——聚类中心;d(xt,θi)——样本xt与θi的差异距离。

利用拉格朗日算子对目标函数求极值可以得到模糊熵聚类算法隶属度矩阵和聚类中心的更新方程(推导过程见文献[10]):

uit={∑Cj=1ed2(xt,θi)ed2(xt,θj)[〛1n}-1θi=∑Tt=1uitxt∑Tt=1uitìîíïïïïïùûúúúúú(3)(4)

1.2聚类数的确定

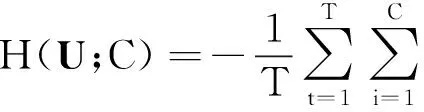
相应地,每一个聚类中心对T个样本构成的可能性分布也有一个香农信息熵,由此定义可能性划分熵为

(5)

范九伦[12]根据Bezdek划分熵和可能性划分熵定义了基于可能性分布的聚类有效性函数(式(6)),并提出当HP(U;C)取得最大值的时候,U为最佳聚类隶属度矩阵、C为最佳聚类数。

(6)

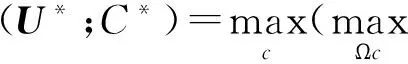
1.3模糊熵系数的确定

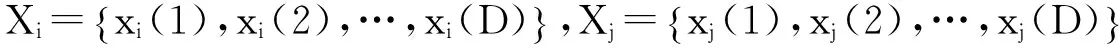
在已知数据样本中选取Xi、Xj、Xk、Xl(i、j、k、l=1，2，…，T)4个样本作为样本空间Ω,其隶属度向量为ui、uj、uk、ul,定义基于距离判定的模糊聚类有效函数为

(7)

式中:P{*}——事件*发生占总样本空间Ω的比例。

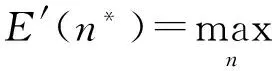
1.4研究步骤

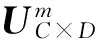
1.5聚类合理性验证

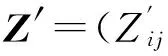
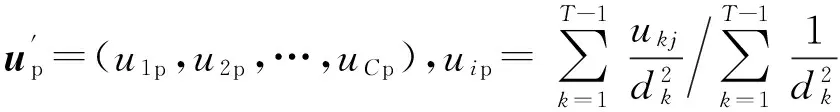
通过真实降雨量矩阵Z、一般情况下的插值雨量矩阵Z′和模糊熵聚类情况下的插值雨量矩阵Z*计算多个交叉统计量[13]。记Xo,Xe分别是已知降雨量数据和交叉检验的插值计算降雨量数据,N为数据个数,各统计量(相关系数R、平均相对误差RMAE、均方根误差RMSE、复合相对误差CRE)计算公式如下:

(8)

相关系数除去了偏差和方差的影响,考虑了插值估计数据与实际数据变化的同步性,表示了插值估计序列替代实际观测序列的潜在能力。平均相对误差和均方根误差反映了插值估计序列与实际序列比较得到的误差平均情况。复合相对误差是描述插值序列与实际序列的相似性指标,该统计量对大误差数据十分敏感。

2　研 究 实 例

2.1数据来源及相似度计算

研究数据来自淮河流域蚌埠站以上区域99个雨量站1953—2013年732个月的降雨量数据,站点基本情况见文献[14]。

淮河流域位于东经112°～118°、北纬31°～35°的区域内,介于长江和黄河两大流域之间。在气候上,它处于南北气候过渡带,降水时空分布严重不均,差异较大。淮河又是我国南北方的一条自然分界线。因此,研究淮河流域的降水时空不确定性具有较高的科学价值。

(9)

(10)

2.2聚类结果

研究发现,当聚类数过大时,出现聚类中心彼此靠近并有重合现象;模糊熵系数小于0.02时聚类划分过于分明,近似硬聚类,当系数大于0.03时聚类间过于模糊。因此,拟定聚类数C=2、3、4、5,模糊熵系数n=0.02、0.022、0.024、0.026、0.028、0.03和停止阈值ε=0.000 1。计算相应的聚类有效性值HP,当C=2、3、4、5时,HP=0.000 4、0.101 1、0.058 4、0.032 6。比较可得,当C=3时,HP取得最大值,因此选取最优聚类数C*=3。

在C*=3的情况下分别计算各模糊熵系数对应隶属度矩阵的距离判定有效性值E,当n=0.02、0.022、0.024、0.026、0.028、0.03时,E=0.761 8、0.763 2、0.764 0、0.764 2、0.762 5、0.764 1。比较可得,在C*=3的情况下,当n*=0.026时E取得最大值。从而得到相应的最优隶属度矩阵U*。聚类结果如图1所示(图中所示星点表示已知雨量站位置)。

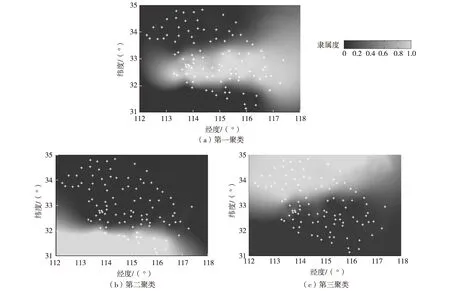
图1　聚类隶属度分布Fig. 1　Distribution of degree of membership in EFC

图1中3幅图分别表示3个聚类的隶属度分布,其中颜色越浅表示该区域对此聚类的隶属度越高,反之越低。中部雨量站集中在第一聚类中,南部雨量站集中在第二聚类中,北部雨量站集中在第三聚类中。可以看出,算法得到的聚类结果有明显的地理位置聚拢性,十分符合实际情况,即地理位置较近的地方,降雨量差异性较小。此外,分区多以纬度划分为主,说明降雨量在纬度变化中的差异变化大,符合我国淮河流域基本自然情况,即南北降雨量差异大、东西降雨量差异小。

表1　交叉验证统计量对比Table 1　Comparison of statistics in cross-validation

2.3验证结果

模糊熵聚类情况下和一般情况下反距离平方加权插值法各交叉统计量如表1所示。

可以看出,与一般情况相比,模糊熵聚类分析情况下,站点雨量插值与测量值相关系数有所提高,各类误差都有所下降,表明模糊熵聚类方法具有一定的优越性。

3　结　　语

通过模糊熵聚类分析,可以深入挖掘降雨信息在流域内的分布,有利于更加深入地探究降雨系统内部的关系,以及多种不确定因素。本文对淮河流域蚌埠站以上区域降雨量数据进行了模糊熵聚类分析,获得模糊熵聚类结果。同时,通过交叉验证法,说明了模糊熵聚类算法在反距离平方加权插值中的实用性。

[1] 石朋,芮孝芳. 降雨空间插值方法的比较与改进[J]. 河海大学学报(自然科学版),2005,33(4):361-365. (SHI Peng, RUI Xiaofang. Comparison and improvement of spatial rainfall interpolation methods. [J]. Journal of Hehai University (Natural Sciences), 2005,33(4):361-365. (in Chinese))

[2] 孔云峰,仝文伟. 降雨量地面观测数据空间探索与插值方法探讨[J]. 地理研究,2008,27(5):1097-1108.(KONG Yunfeng, TONG Wenwei. Spatial exploration and interpolation of the surface precipitation data[J]. Geographical Research, 2008, 27(5):1097-1108. (in Chinese))

[3] 张继国, 谢平, 龚艳冰, 等.降雨信息空间插值研究评述与展望[J].水资源与水工程学报, 2012, 23(1):6-9. (ZHANG Jiguo, XIE Ping, GONG Yanbing, et al. Review and perspectives of the research on spatial interpolation of rainfall information [J]. Journal of Water Resources and Water Engineering, 2012,23(1):6-9.(in Chinese))

[4] 李生辰, 徐亮, 郭英香, 等.近34a青藏高原年降水变化及其分区[J].中国沙漠, 2007, 27(2):307-314. (LI Shengchen, XU Liang, GUO Yingxiang, et al. Change of annual precipitation over QinghaiXizang Plateau and subregions in recent 34 years [J]. Journal of Desert Research, 2007, 27(2): 307-314. (in Chinese))

[5] 杨绚, 李栋梁.中国干旱气候分区及其降水量变化特征[J].干旱气象, 2008, 26(2):17-24. (YANG Xuan, LI Dongliang. Precipitation variation characteristics and arid climate division in China [J]. Arid Meteorology, 2008, 26(2):17-24.(in Chinese))

[6] 郑永宏, 林爱文, 代侦勇.湖北省降水分区研究[J].长江流域资源与环境, 2012, 21(7):859-863. (ZHENG Yonghong, LIN Aiwen, DAI Zhenyong. Research on precipitation regionalization in Hubei Province [J]. Resources and Environment in the Yangtze Basin, 2012,21(7):859-863.(in Chinese))

[7] 雷鸣. 模糊聚类新算法的研究[D].天津:天津大学,2007.

[8] 冀鸿兰,卞雪军,徐晶. 黄河内蒙古段流凌预报可变模糊聚类循环迭代模型[J]. 水利水电科技进展,2013,33(4):14-17. (JI Honglan, BIAN Xuejun, XU Jing. Variable fuzzy clustering loop iteration model for ice-run forecast in Inner Mongolia reach of Yellow River [J]. Advances in Science and Technology of Water Resources, 2013, 33(4):14-17.(in Chinese))

[9] 樊哲超,陈建生,董海洲,等. 应用环境同位素和模糊聚类方法研究堤防渗漏[J]. 水利水电科技进展,2005,25(2):8-10,57. (FAN Zhechao, CHEN Jiansheng, DONG Haizhou, et al. Application of environmental isotope and fuzzy clustering method to study of seepage from dykes [J]. Advances In Science and Technology of Water Resources, 2005, 25(2):8-10,57.(in Chinese))

[10] WU Xiaohong, ZHOU Jianjiang. Possibilistic fuzzy entropy clustering[J]. Journal of Computational Information Systems, 2007, 3(1):25-33.

[11] BEZDEK J C. Pattem recognition with fuzzy objective function algorithms [M]. New York: Plenum, 1981.

[12] 范九伦. 模糊聚类新算法与聚类有效性问题研究[D].西安:西安电子科技大学,1998.

[13] 熊秋芬,黄玫,熊敏诠,等. 基于国家气象观测站逐日降水格点数据的交叉检验误差分析[J]. 高原气象,2011,30(6):1615-1625.(XIONG Qiufen, HUANG Mei, XIONG Minquan, et al. Cross-validation error analysis of daily gridded precipitation based on China meteorological observation [J]. Plateau Meteorology,2011,30(6):1615-1625. (in Chinese))

[14] 张继国.降雨时空分布不均匀性信息熵研究[D].南京:河海大学,2004.

Fuzzy entropy clustering analysis of spatial distribution of precipitation

ZHANG Jiguo1, GUAN Yaozong2, ZHU Yongzhong2

(1.InstituteofInformationStatisticsandManagementofWaterResources,

In order to improve the accuracy of precipitation interpolation and fully explore the information regarding precipitation variables, fuzzy entropy clustering (FEC) was carried out at rain gauge stations in a basin. A clustering validity function, based on possibility distribution and distance determination, was used to determine the fuzzy entropy coefficient and the number of clusters, so as to obtain the fuzzy clustering results and improve the original interpolation method. Based on data from 99 rain gauge stations located above the Bengbu Station in the Huaihe River Basin, cross validation was conducted under non-clustering and FEC conditions. The results demonstrate that FEC improves the precipitation accuracy in the inverse distance squared interpolation method.

spatial distribution of precipitation; accuracy of precipitation data; fuzzy entropy clustering (FEC) analysis; clustering validity analysis; precipitation interpolation

1000-1980(2016)04-0353-05

10.3876/j.issn.1000-1980.2016.04.012

2015-10-17

江苏省自然科学基金(BK20131135);江苏省自然科学青年基金(BK20130242)

张继国(1956—),男,湖北汉川人,教授,主要从事水文不确定性分析、信息熵理论与方法研究。E-mail:zhangjg@hhuc.edu.cn

P467

A