确定GPS接收机码间偏差的一种新算法

田林亚，熊欢欢，石　超，祖　滢

(河海大学地球科学与工程学院，江苏 南京　211100)



确定GPS接收机码间偏差的一种新算法

(河海大学地球科学与工程学院，江苏 南京211100)

针对目前求解GPS接收机码间偏差(B)的主要方法(球谐函数模型法、曲面拟合模型法等)存在计算繁琐和效率不高等问题，研究并提出一种新的计算方法，即利用双频载波相位平滑伪距数据以及CODE提供的全球电离层VTEC地图和卫星B值，通过旋转地图内插VTEC以及伪距差分进行单站GPS接收机B值的解算。采用此方法和IGS跟踪站的观测数据解算GPS接收机的B值，并与CODE 提供的跟踪站的B值进行比较，结果表明，这种新算法能够以优于0.4 ns 的精度确定GPS接收机的B值。

GPS；接收机；码间偏差；CODE；天顶方向总电子含量；相位平滑伪距；旋转地图；电离层格网

GPS码间偏差(difference code bias，B)是指由于硬件延迟造成同一时间不同频率或同一频率上不同伪码观测量之间的时间偏差，包含GPS接收机码间偏差和卫星码间偏差[1-3]。按照不同的接收机类型，接收机码间偏差可分为P1/P2、C1/P1和C2/P2等3种码间偏差；卫星P1/P2码间偏差通过导航电文播发给用户，对应于导航电文中的τGD字段。IGS发布的P1/P2码间偏差(BP12)与导航电文发布的τGD关系一般表示为[4-5]

τGD=1.55BP12+d

(1)

式中：d——常数差异。

目前，求解GPS接收机B值的方法较多，如CODE的球谐函数模型法、曲面拟合模型法等，这些方法都将卫星及接收机的B值视为未知参数参与平差解算。有人利用球谐函数进行区域电离层建模，从而解算接收机B值[1，3]，但这种方法的计算效率不高。有人利用GIM提供的电离层数据内插VTEC，用3维B-SPLINE 模型来表述误差项，通过方差分量估计法解算接收机B值[6-8]，但这种计算方法十分繁琐。本文提出一种解算GPS接收机B值的新算法，即利用旋转地图电离层格网内插及伪距观测值之差进行接收机B值的解算，在提高解算效率的同时，有效保证了接收机B值的解算精度。

1　码间偏差的计算原理

考虑GPS卫星与接收机的硬件延迟时，GPS伪距观测方程可以表示为

(2)

式中：Pi——第i频点上的伪距观测值；P0——理论卫星至接收机的距离；I——观测历元电离层改正因子；fi——对应的载波频率；c——光速；bRi、bSi——第i频点上接收机及卫星的硬件延迟误差；δtrop——对流层延迟改正项；δRt、δSt——接收机与卫星的钟差；ε——测量噪声，包括多路径效应。

将同一历元P1、P2伪距观测方程直接求差，可得组合观测方程：

(3)

式中：BS——卫星P1/P2的码间偏差；BR——接收机P1/P2的码间偏差；ε′——组合观测噪声。

由于P1-P2的精度较低(大约为0.43 m)，而载波相位观测值λ1φ1-λ2φ2的精度较高(一般为毫米级)[6]，可先采用GF-MW组合法进行载波相位观测值的周跳探测及修复[9-12]，再利用已完成周跳修复后的载波相位观测值对P1、P2伪距观测值进行平滑，以此提高B的解算精度。采用Hatch滤波和双频载波相位观测值平滑P1、P2伪距观测值的逐历元递推公式如下：

(4)

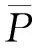
由式(3)可以看出，解算接收机B值的精度与卫星B值及电离层延迟精度有关。解算接收机B值的方法一般有2种：一种是建立区域电离层模型，同时解算卫星B参数、电离层模型参数及接收机B参数；另一种是将IGS发布的全球电离层数据作为已知值，经电离层参数改正后再解算接收机B参数。

将CODE提供的卫星B参数作为已知值，由式(3)及式(4)可得解算接收机B值的观测方程：

y=mfVTECF(z′)+cBR+ε′

(5)

其中

式中：mf——频率相关因子；VTEC——天顶方向的总电子含量；F(z′)——投影函数；z′——穿刺点(IPP)的天顶距。

GPS常用的投影函数有Klobuchar模型投影函数、Q因子投影函数、分段提取的电离层投影函数等[12-13]，其中电离层投影函数为

(6)

式中：R——地球平均半径，一般取为6 371 km；H——单层电离层模型高度，一般取为506 km；α——改正系数[9]。

利用球谐函数模型解算接收机B值时，VTEC需要用球谐函数建立区域电离层模型，联合解算模型参数以及接收机B值，球谐函数模型为[13]：

(7)

其中

s′=λ-λ0

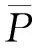
由于利用球谐函数建立区域电离层模型需要引入大量的待估球谐函数系数，例如将球谐函数展开至4阶时需要引入的待估球谐函数系数多达25个，且需要构建电离层模型，因此，用这种方法解算接收机B值的效率不高，计算也十分繁琐。

2　码间偏差的新算法

由上可知，基于球谐函数模型解算接收机B值的主要工作是利用球谐函数模型建立区域电离层模型，解算天顶方向的总电子含量。鉴于CODE、JPL等机构会发布每日全球或区域电离层产品和卫星码间偏差(副产品，每日1套)，还增加了部分IGS跟踪站的接收机码间偏差，CODE发布的每日IONEX1.0文件中含有25张VTEC地图，对应于每日的0:00—24：00整点时刻，JPL发布的每日IONEX1.0文件中含有13张VTEC地图，对应于0：00,2：00,…,24：00，因此，利用这些机构发布的电离层产品可以内插出任意时刻、任意地心经纬度(φ,λ)处的VTEC[14-15]。取任意2个相邻时刻VTEC地图内插VTEC的算法如下：

(8)

其中

Ti≤t≤Ti+1

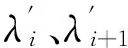
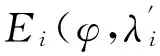
s=λ+t-12

(9)

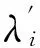
(10)

将式(9)代入式(10)可得

(11)

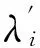
在考虑接收机B值与卫星B值的情况下，对于双频GPS观测数据，测站至卫星路径上的总电子含量的观测方程如下[8]：

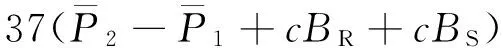
(12)

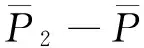
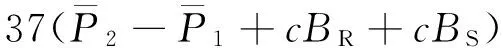
(13)

新的观测方程中只含有接收机B一个参数，解算过程中观测量依据卫星高度角加权，权函数可表示为

(14)

3　计算结果分析

为了验证本文提出新算法的可靠性及解算精度，利用中国区域内的BJFS、BJNM、CHAN、URUM 等4个IGS跟踪站2015年3月16—22日7 d的观测数据，分别解算各站接收机B值，并与CODE、JPL机构提供的数据进行对比，分析新算法的可靠性；利用BJFS、URUM 2015年3月1—30日的观测数据，分析新算法的解算精度。所用数据均可在IGS网站下载得到。

3.1算法可靠性分析

使用上述4个IGS跟踪站的数据，首先对原始观测数据进行处理，处理过程中剔除卫星高度角小于10°的观测值和同一卫星连续观测少于10个历元的观测值，因为CODE提供的VTEC地图每天有25张，每张VTEC地图时间间隔较JPL的短，为提高VTEC内插精度，在内插穿刺点VTEC、获取各卫星B值信息时，均采用CODE提供的IONEX文件给出的数值。

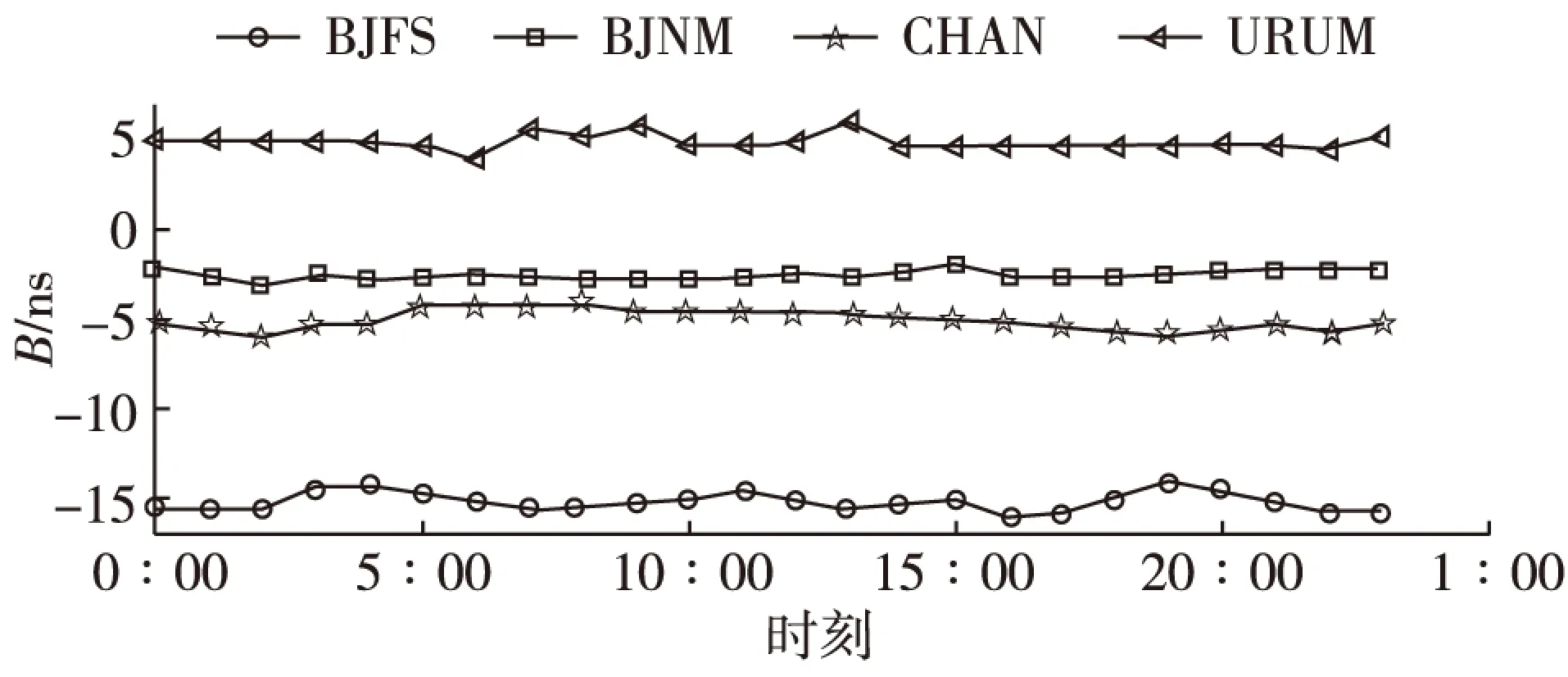
图1　接收机1 d的B值变化Fig. 1　Change of receiver’s B in one day

为了验证接收机B值每日的变化趋势是否符合实际，采用本文研究的新算法解算了4个跟踪站3月16—22日内每天24 h的接收机B值。以3月19日的4个跟踪站为例，图1给出了各站全天的接收机B值解算结果。

由图1可以看出，在1 d内接收机B值的变化不大，均在某一值附近波动。在以往的解算过程中，通常认为1 d内接收机B值与卫星B值为固定值，IGS等机构所发布电离层文件中也是以日为单位给出的，因此新算法所得的B值在1 d内的变化趋势符合实际情况。

为了验证解算结果的可靠性，需要以日为单位解算4个跟踪站每天的B值，并与CODE、JPL等机构发布的跟踪站B值对比。图2为1周内4个跟踪站B值解算结果与CODE、JPL发布值的对比。

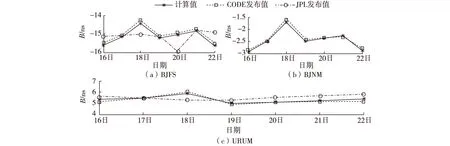
图2　1周的B值对比Fig. 2　Comparison of B values over one week

由于CODE没有发布CHAN站的B值，JPL没有发布BJNM、CHAN站的B值，因此，图2没有给出相应的值。由图2可以看出，在1周时间内，新算法解算的B值与CODE、JPL发布值相差均不超过1 ns，即使3月18日BJNM站B值变化幅度较大，新算法的解算结果仍能很好地符合CODE的发布值，说明新算法的解算结果是可靠的。

3.2计算精度分析

采用同样的数据处理方法和接收机B值的新算法，解算BJFS、URUM跟踪站3月1—30日的接收机B值，并与CODE、JPL发布的B值作差，分析新算法的解算精度。图3中，差值为0表示相应机构没有发布该日此跟踪站的B值。

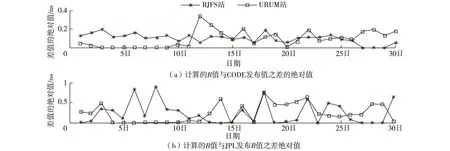
图3　1个月内B的差值Fig. 3　Difference in B values obtained from different methods over one month

从图3可以看出，本文新算法解算的接收机B值与CODE机构发布的B值的差值基本保持在0.2 ns以内，与JPL机构发布B值的差值也保持在1 ns以内，其中绝大部分在0.5 ns以内，CODE与JPL发布值相差在1 ns以内。之所以解算出的B值相对于JPL给出的值差值较大，原因可能是在内插穿刺点VTEC与获取各卫星B值时均采用的是CODE提供的IONEX文件，而CODE与JPL提供的IONEX文件中VTEC值和各卫星B值实际是有差异的，所以解算结果更接近CODE发布的跟踪站B值。以CODE提供的B值为真值，新算法解算的2个跟踪站BJFS、URUM 1个月的B值中误差分别为0.113 6 ns、0.141 4 ns，中误差均小于0.2 ns，因此本文提出的新算法具有较高的解算精度。

4　结　　语

本文提出的利用单站双频GPS观测值，采用旋转地图内插获取VTEC，解算接收机B值的算法，与传统的利用多站观测数据建立区域电离层模型相比，提高了B值的解算效率。采用新算法解算的B值与CODE机构发布的B值相比，差值基本保持在0.2 ns以内，比传统算法的解算精度略有提高。另外，采用新算法解算的B值精度与采用的电离层格网精度强相关，在IGS跟踪站较少和电离层格网精度较低的地区，解算精度有待进一步研究和提高。

[1] 宋小勇, 杨志强, 焦文海,等. GPS接收机码间偏差(DCB)的确定[J]. 大地测量与地球动力学, 2009, 29(1):127-131.(SONG Xiaoyong, YANG Zhiqiang, JIAO Wenhai, et al. Determination of GPS receiver’s DCB[J]. Journal of Geodesy and Geodynamics, 2009, 29(1):127-131. (in Chinese))

[2] JIN Rui, JIN Shuanggen, FENG Guiping. M_DCB: matlab code for estimating GNSS satellite and receiver differential code biases[J]. Gps Solutions, 2012, 16(4):541-548.

[3] 张伟, 邱卫宁, 畅鑫. 基于球谐函数模型的GPS差分码延迟估计[J]. 测绘通报, 2013，41(6):19-21.(ZHANG Wei, QIU Weining, CHANG Xin. Estimation of GPS differential code delay based on spherical harmonic function model[J]. Bulletin of Surveying and Mapping, 2013, 41(6):19-21. (in Chinese))

[4] 耿长江. 利用地基GNSS数据实时监测电离层延迟理论与方法研究[D]. 武汉：武汉大学, 2011.

[5] 魏传军. 基于地基GNSS观测数据的电离层延迟改正研究[D]. 西安：长安大学, 2014.

[6] HONGC K, GREJNER-BRZEZINSKA D A, KWON J H. Efficient GPS receiver DCB estimation for ionosphere modeling using satellite-receiver geometry changes[J]. Earth Planets & Space, 2008, 60(11):25-28.

[7] 谢益炳, 陈俊平, 伍吉仓. 一种确定单站接收机码间偏差的新算法[J]. 大地测量与地球动力学, 2013, 33(4):142-145. (XIE Yibing, CHEN Junping, WU Jicang. A new algorithm for determining GPS single receiver DCB[J]. Journal of Geodesy and Geodynamics, 2013, 33(4):142-145. (in Chinese))

[8] 章红平. 基于地基GPS的中国区域电离层监测与延迟改正研究[D]. 上海：中国科学院研究生院(上海天文台), 2006.

[9] KESHINM. A new algorithm for single receiver DCB estimation using IGS TEC maps[J]. GPS Solutions, 2012, 16(3):283-292.

[10] 陈央央. GPS周跳探测与修复问题研究[D]. 西安：长安大学, 2014.

[11] PARK B, KEE C. Optimal hatch filter with a flexible smoothing window width[J]. Journal of Navigation, 2005, 61(3):435-454.

[12] 王维, 王解先, 高俊强. GPS周跳探测的方法研究[J]. 武汉大学学报：信息科学版, 2010(6):687-690. (WANG Wei, WANG Jiexian, GAO Junqiang. Cycle slip detection of GPS[J]. Geomatics and Information Science of Wuhan University, 2010(6):687-690. (in Chinese))

[13] 李征航, 黄劲松. GPS测量与数据处理[M]. 2版.武汉：武汉大学出版社, 2012:104-105.

[14] 吴继忠，高俊强，李明峰. IGS精密星历和钟差插值方法的研究[J]. 工程勘察，2009，37(7)：52-54.(WU Jizhong, GAO Junqiang, LI Mingfeng. Research on interpolation method for IGS precise ephemeris and clockbias[J]. Geotechnical Investigation & Surveying,2009,37(7):52-54.(in Chinese))

[15] 王五魁, 刘长建, 吴洪举. IGS电离层VTEC产品内插算法解析[J]. 全球定位系统, 2013(6):17-21.(WANG Wukui, LIU Changjian, WU Hongju. Interpolating algorithm analysis of IGS ionosphere VTEC product[J]. Gnss World of China, 2013(6):17-21. (in Chinese))

A new algorithm for determining GPS receiver’s differential code bias

TIAN Linya, XIONG Huanhuan, SHI Chao, ZU Ying

(SchoolofEarthScienceandEngineering,HohaiUniversity,Nanjing211100,China)

Major methods for determining a GPS receiver’s differential code bias (B), including the spherical harmonic function model and surface fitting model, have a high degree of computational complexity and poor efficiency. Based on the pseudorange data with carrier phase smoothing, global maps of vertical total electron content (VTEC) of the ionosphere, and satelliteBvalues provided by CODE, this paper proposes a new algorithm for determining the single GPS receiver’sBthrough interpolatedVTECvalues from rotated maps and the pseudorange difference. The GPS receiver’sBvalues were estimated with the proposed method and observed data at IGS tracking stations, and were compared with those at the tracing stations provided by CODE. The results show that the new method can determine the GPS receiver’sBwith an accuracy higher than 0.4 ns.

GPS; receiver; differential code bias; CODE; vertical total electron content; carrier phase smoothed pseudorange; rotated map; ionosphere grid

1000-1980(2016)04-0330-05

10.3876/j.issn.1000-1980.2016.04.008

2015-10-15

田林亚(1963—)，江苏淮安人，教授，博士，主要从事卫星导航与定位研究。E-mail：lytian@sina.com

P228.4

A