基于Copula熵理论的大坝渗流统计模型因子优选

李小奇,郑东健,鞠宜朋

(1.河海大学水文水资源与水利工程科学国家重点实验室，江苏 南京　210098；2.河海大学水资源高效利用与工程安全国家工程研究中心，江苏 南京　210098；3.中国电子科技集团公司第十五研究所，北京　100083)



基于Copula熵理论的大坝渗流统计模型因子优选

李小奇1,2,郑东健1,2,鞠宜朋3

(1.河海大学水文水资源与水利工程科学国家重点实验室，江苏 南京210098；2.河海大学水资源高效利用与工程安全国家工程研究中心，江苏 南京210098；3.中国电子科技集团公司第十五研究所，北京100083)

针对大坝渗流统计模型需要考虑较多的前期项，造成参选的因子数量较大，进而导致常规方法的建模误差较高的问题，研究引入Copula熵理论，利用Copula熵和偏互信息(partial mutual information，PMI)相结合的方法，对输入因子的选取进行优化。针对Copula熵的求取，Copula函数采用Gumbel函数，分布采用柯西分布代替正态分布，并引入Hample准则来精确选取因子。将该方法在糯扎渡大坝渗流监测中进行应用，并与常规的因子选择方法进行对比分析，结果表明，采用基于Copula熵的因子优化选取方法的渗流统计模型具有更好的预测效果。

大坝安全监控；渗流统计模型；Copula熵；输入因子；偏互信息

HohaiUniversity,Nanjing210098,China;2.NationalEngineeringResearchCenterofWaterResourcesEfficientUtilizationandEngineeringSafety,HohaiUniversity,Nanjing210098,China;3.TheFifteenthResearchInstitute,ChinaElectronicTechnologyGroupCorporation,Beijing100083,China)

随着大坝安全监测对预测模型的精度要求越来越高，影响模型精度的预报因子选取日益重要。目前，渗流统计模型预报因子的选择最常用的是线性相关系数[1]、主成分分析、灰色关联度分析等方法。表1列举了渗流统计模型因子的几种主要选择方法，并对其优劣进行了简要分析。

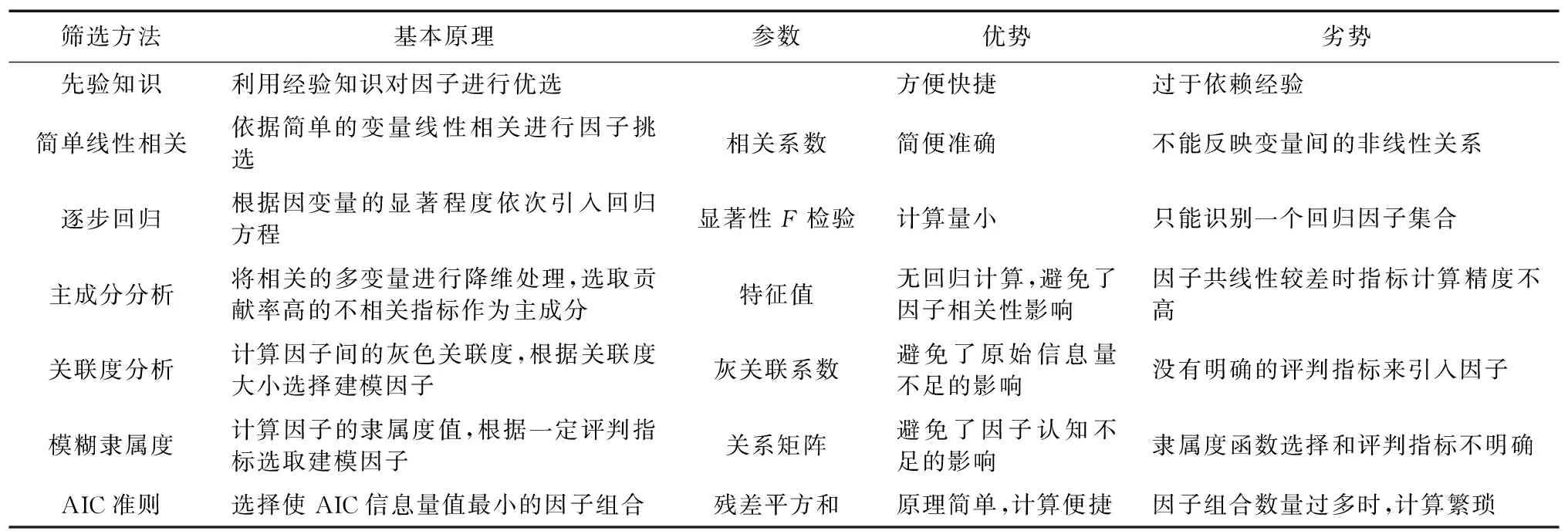
表1　渗流统计模型因子选择的几种主要方法Table 1　Several methods for input factor selection of seepage statistical model

先验知识方法最为简便，但误差也最大。逐步回归分析中，由F检验剔除的因子有可能组成最佳因子集，并且在对因子集进行联合分析时只能识别一个因子集合[2]。主成分分析法对相关变量的要求较高，当

变量的共线性较差时，降维处理得到的综合指标精度也较低[3]。利用关联度进行因子选择时，只能将因子按照关联度值进行排序，没有具体引入指标[2]。模糊隶属度函数选择对样本分布的依赖性较大，隶属度函数选择对结果精度的影响较高[4]。AIC信息量准则法中，计算量与因子组合数量成正比，当因子组合过多时工作量巨大[5]。鉴于以上不足，需要提出一种新的理论来满足大坝安全监控中对渗流统计模型因子选择的需求。

目前，一种可供选择的方法是互信息(mutual information, MI)法以及MI改进算法[6]。赵铜铁钢等[7]利用MI法选择了神经网络模型的输入因子。卢迪等[8]利用互信息法对BP网络模型的中长期径流预报因子进行了筛选。Sharma[9]改进了MI法，提出偏互信息(partial mutual information, PMI )的概念，并得到了广泛应用。Kan等[10]利用PMI法对集合神经网络(ENN)的径流预报因子进行了优化选取。Yuan等[11]利用PMI法对时间序列模型的输入因子进行了选取。应用和研究证明了PMI法可以有效提高模型因子选择的精度。然而，PMI法仍有缺陷：(a)水位、位移、沉降等均为连续变量，而PMI主要基于离散数据；(b)对多元分布变量的边缘和联合概率密度进行估计时，概率密度函数难以求得[6-7]。

针对上述不足，本文提出了Copula熵和PMI相结合的方法。在已有的大坝渗流统计模型基础上，通过专家经验确定备选因子集，采用Copula函数和信息熵结合的Copula熵法计算PMI值，然后基于PMI的选入准则，对大坝渗流影响量的实测数据进行计算，确定最终的输入因子集。最后，将此方法在糯扎渡大坝的渗流监测中进行了应用和对比。

1　基 本 原 理

1.1渗流统计模型方程

渗流量的大小反映了混凝土坝坝体和地基帷幕以及土石坝防渗体的防渗效果，是评价大坝运行安全的重要依据。大坝渗流主要受上下游水位、降雨和温度的影响，模型方程表示为[12]

Q=QSH+QXH+QR+QP+Qθ

(1)

式中：Q——渗流量实测值；QSH——上游水位分量；QXH——下游水位分量；QR——温度分量；QP——降雨分量；Qθ——时效分量。

1.2Copula函数

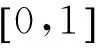
F(x1,…,xn)=C(F1(x1),…,Fn(xn))

(2)

式中：F——n维变量的联合累积分布函数；x1,…,xn——n个随机变量；Fi——各变量的边缘分布函数。

如果F1…Fn是连续的，那么C是唯一的；反之C不唯一。

在多变量的研究中，Archimedean型Copula函数具有模型构造方便和计算简单的优点，因此应用广泛[14]。本研究采用Archimedean型最常用的Gumbel Copula函数来进行计算，它主要描述例如某变量剧增时，效应量会发生同样剧增情形时的正相关特性。为了便于计算，本文一律取二维变量的情形，它的二维联合分布函数和密度函数如下：

(3)

(4)

式中：u——变量x的边缘分布F(x)；v——变量y的边缘分布F(y)；θ——Gumbel Copula函数的参数，在[1,+)内取值。

1.3Copula熵

熵理论是1948年Shannon将玻尔兹曼熵的概念引入信息论中，用来度量随机事件的不确定性或信息量的方法[15]。大坝监测信息多为连续随机变量，n维随机变量的联合熵可以表示为

(5)

式中：H(x)——n维连续性随机变量的熵函数；f(x)——变量x的概率密度函数，可用分布函数的偏微分来表示。

若式(3)中的u=F(x)，v=F(y)，则Copula熵的表达式为

(6)

对Copula熵的求解，转化为求变量x和y的边缘分布F和Copula联合分布的参数θ的过程。θ可以通过Kendall系数来求取[16]，它与Kendall系数τ的关系为

(7)

本文选取柯西分布函数作为随机变量ξ的边缘分布函数，与正态分布相比，柯西分布产生的随机点具有较广泛的覆盖范围，能真实地反映随机向量的分布情况，同时能较快摆脱局部最优值的现象[17]。柯西分布的概率密度函数和分布函数分别为

(8)

(9)

式中：μ——分布峰值位置的位置参数；γ——最大值1/2处的1/2宽度的尺度参数。

对μ采用中位数作为估计量，对γ采用分位数作为估计量[18]。假设求得μ的中位数为μn/2，则γ=μ3n/4-μn/2。

求得单变量的边缘分布函数F(x)的参数μ、γ后，代入式(3)的联合分布函数C(u,v)，再根据求得的θ，即可得到Gumbel Copula分布函数和密度函数。然后将联合分布密度函数带入式(6)，求得Copula熵的值。

1.4Copula熵的PMI计算

偏互信息(PMI)是Sharma提出的，它度量了在消除多余变量影响的条件下，某两变量之间的相关性。通过计算某两变量的CPMI值，设定一定的过滤标准，即可得到筛选后的输入因子集合。以二维情形计算，假设两变量为x、y，由偏互信息的定义可知：

(10)

其中

式中：x′——x的残余信息；y′——y的残余信息；Z2——二级备选因子集合。

(11)

式中：N——样本数；αj——平滑参数，本文取高斯核密度估计的窗宽进行计算[9]；ξ——高斯分布的参数；Szz——Z2中变量Z2i样本的协方差；Sxz——变量x和Z2中变量Z2i样本的互协方差。

根据多维联合熵的定义，多维变量的联合熵可以用n个变量的边缘熵的和与Copula函数熵的和来表达。由于du=dxf(x)，dv=dyf(y)，f(x,y)=c(u,v)f(x)f(y)，二维联合熵的表达式可以写为

(12)

对于本文二维变量(x′,y′)的情形，式(12)可以写为

H(x′,y′)=H(x′)+H(y′)+HC(u′,v′)

(13)

式(13)代入式(10)可知，CPMI=-HC(u′,v′)，即偏互信息为Copula函数的负熵，u′为变量x′的分布函数，v′为变量y′的分布函数。通过Copula熵计算PMI值的过程如图1所示。

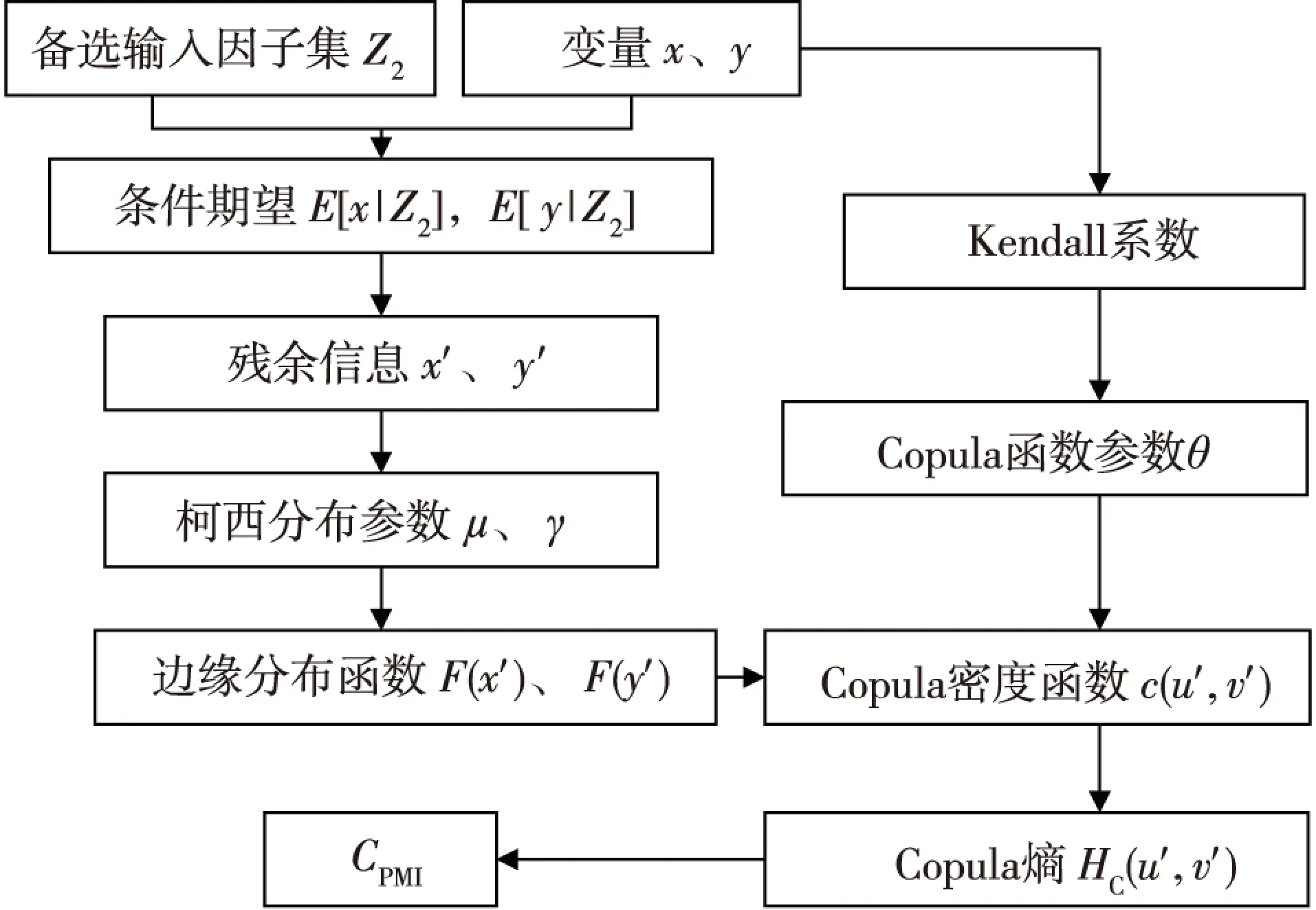
图1　CPMI值计算过程Fig. 1　Calculation process of CPMI

1.5因子选入准则

PMI算法需要给定一个标准，来判定CPMI多大时将变量x纳入模型的输入因子集。本文采用Fernando和May等推荐的Hampel检验作为算法的停止准则[19-20]，其表达式为

(14)

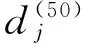
根据标准差的3σ准则，当Hj>3时，因子被选入。

2　实 例 分 析

2.1概况

土石坝渗流一直是坝体安全监测的关键指标，本研究以糯扎渡黏土心墙堆石坝为例。糯扎渡大坝是世界同类型中第三高坝，位于中国云南省澜沧江上，最大坝高261.5 m，坝顶长度627.87 m，坝顶宽度18 m，水库正常蓄水位812 m。坝体于2008年11月开始填筑，2012年12月21日填筑到坝顶。蓄水初期水位变化较大，加上坝体填筑过程中的数据缺失以及外部环境的改变，对坝体安全监测模型的因子选择造成了障碍。因此，考虑利用Copula熵和PMI法相结合的理论进行计算。心墙渗流是土石坝渗漏监测的重点，这里以蓄水期最关键的心墙中下部617m高程的DB-C-P-14～DB-C-P-17渗压计测点为例，取2011-11-30—2013-01-18时段内的数据进行分析。为了叙述方便，以DB-C-P-14测点的计算过程为例进行演示。

2.2备选因子

通过资料分析和知识经验，考虑温度对坝体材料的影响，引入上游水位HSH、下游水位HXH、温度T、降雨P和时效θ等作为备选因子来进行筛选，具体结果见表2。

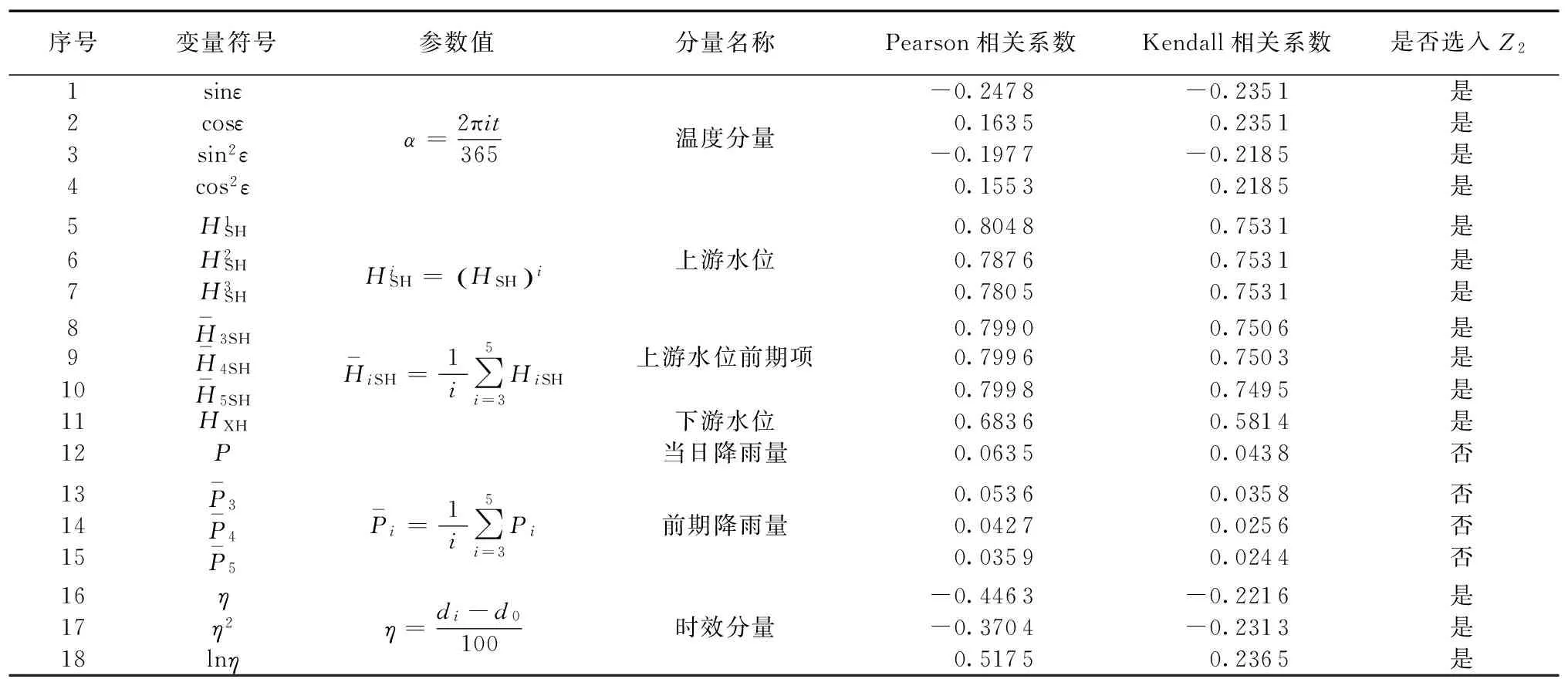
表2　二级输入因子集Z2统计表Table 2　Statistical table of second-level input factor set Z2

2.3因子优选

2.4结果对比

为了显示方法的优越性，将利用经验知识、相关性和Copula熵得到的输入因子集合进行了对比分析和计算，模型采用逐步回归法，结果如表3所示。针对2011-11-30—2013-01-18数据进行分析，以2011-11-30—2013-01-01作为拟合区间，2013-01-01—2013-01-18为预测区间，得到拟合结果如图4所示，典型日期预测结果如表4所示。由图表对比可知，采用Copula熵法输入因子的渗流统计模型拟合值更贴近实测值，拟合精度和预测精度都更高。

表3　DB-C-P-14～DB-C-P-17测点拟合结果对比Table 3　Comparison of fitted results at monitoring points DB-C-P-14 through DB-C-P-17

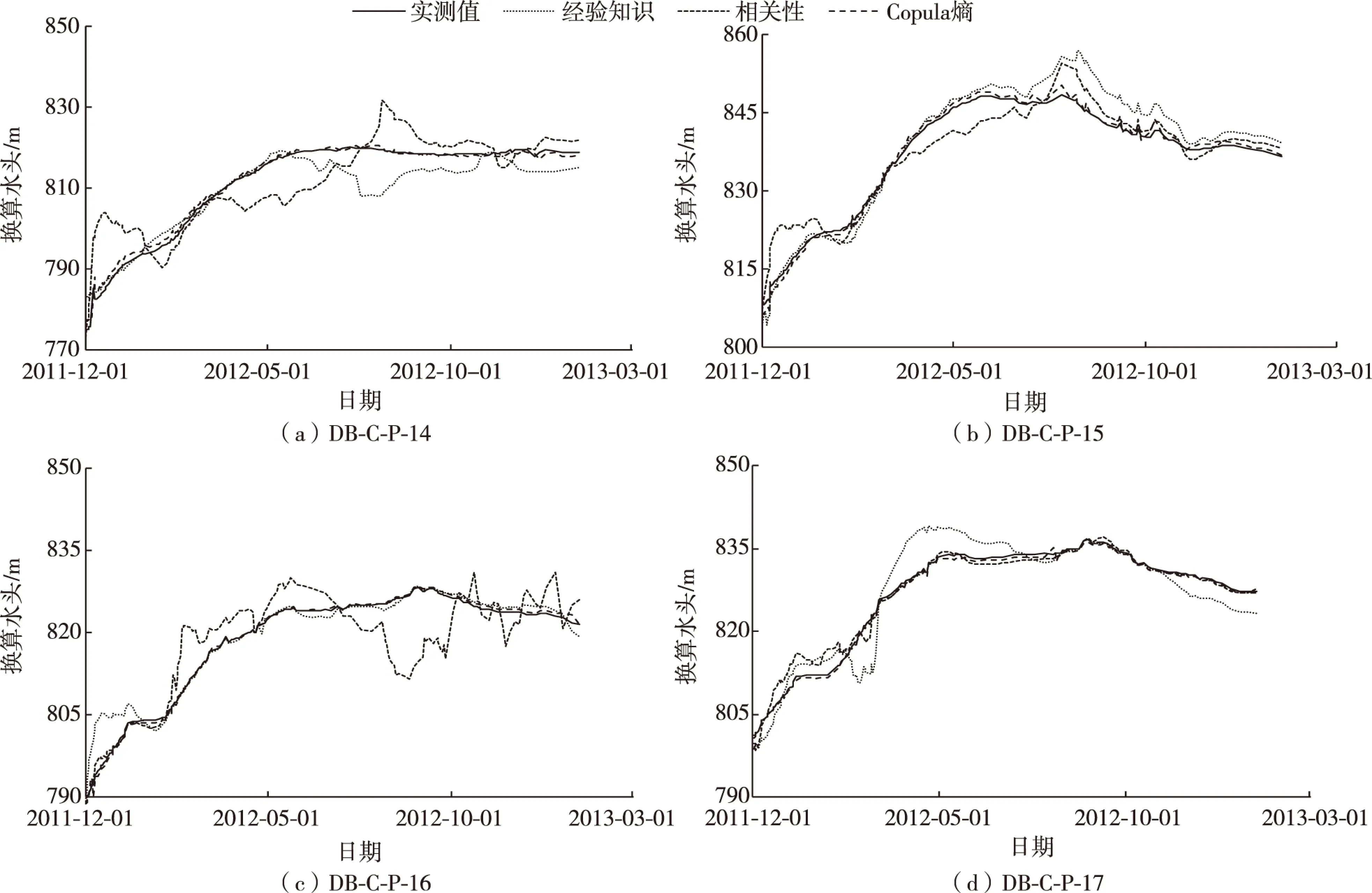
图2　模型拟合曲线对比Fig. 2　Comparison of fitted curves by present model for different monitoring points

表4　DB-C-P-14～DB-C-P-17测点水头预测结果对比Table 4　Comparison of predicted results of hydraulic heads at monitoring points DB-C-P-14 through DB-C-P-17　m

3　结　　论

a. 依据大坝监测样本，采用Archimedean型Copula函数进行计算，为了计算简便，采用二维的Gumbel Copula函数。利用Kendall秩相关系数，求解了Gumbel Copula函数的相关参数。

b. 对于变量的边缘分布，采用柯西分布代替正态分布，并利用中位数和分位数的方法，对柯西分布参数进行求取，从而进一步精确了Gumbel Copula联合分布函数。

c. 引入PMI方法，推导得到Copula函数的负熵等于偏互信息值。通过PMI的计算，并引入Hample检验作为停止准则，建立了因子引入的标准和具体步骤。

d. 建立基于Copula熵的因子选择流程，并根据优选后的因子建立了渗流统计模型。通过与常规方法对比，证明新的因子优化方法建立的预测模型效果更好。

[1] 陈西江, 鲁铁定, 谭成芳. 大坝位移BP网络模型影响因子的优选[J]. 江西科学, 2010, 28(1):72-76. (CHEN Xijiang, LU Tieding, TAN Chengfang. Optimization for influence factors of dam displacement base on BP neural network model [J]. Jiangxi Science, 2010, 28(1):72-76.(in Chinese))

[2] 姚远, 李姝昱, 张博. 逐步回归-PLS模型在大坝位移监控中的应用[J].水电能源科学, 2011,29(4):81-82.(YAO Yuan, LI Shuyu, ZHANG Bo. Application of stepwise regression-PLS model to dam displacement monitoring [J]. Water Resources & Power, 2011, 29(4):81-82. (in Chinese))

[3] YU Hong, WU Zhongru, BAO Tengfei, et al. Multivariate analysis in dam monitoring data with PCA[J]. Science China Technological Sciences, 2010, 53(4):1088-1097.

[4] 王季方, 卢正鼎. 模糊控制中隶属度函数的确定方法[J]. 河南科学, 2000, 18(4): 348-351. (WANG Jifang, LU Zheng ding. The determine method of membership function in fuzzy control [J]. Henan Science, 2000, 18(4): 348-351. (in Chinese))

[5] HU S. Akaike information criterion [M]. North Carolina State: Center for Research in Scientific Computation, 2007.

[6] CHEN Lu, GUO Shenglian. Copula entropy and its application in hydrological correlation analysis [J]. Journal of Water Resources Research, 2013, 2(2): 103-108.

[7] 赵铜铁钢, 杨大文. 神经网络径流预报模型中基于互信息的预报因子选择方法[J]. 水力发电学报, 2011, 30(1):24-30. (ZHAO Tongtiegang, YANG Dawen. Mutual information-based input variable selection method for runoff-forecasting neural network model [J]. Journal of Hydroelectric Engineering, 2011, 30(1):24-30. (in Chinese))

[8] 卢迪, 周惠成. 基于互信息量与BP神经网络的中长期径流预报方法研究[J]. 水文, 2014,4(4):8-14.(LU Di, ZHOU Huicheng. Medium and long-term runoff forecasting based on mutual information and BP neural network [J]. Journal of China Hydrology, 2014,4(4):8-14. (in Chinese))

[9] SHARMA A. Seasonal to interannual rainfall probabilistic forecasts for improved water supply management(part 1): a strategy for system predictor identification [J]. Journal of Hydrology, 2000, 239(1): 232-239.

[10] KAN Guangyuan, YAO Cheng, LI Qiaoling, et al. Improving event-based rainfall-runoff simulation using an ensemble artificial neural network based hybrid data-driven model [J]. Stochastic Environmental Research & Risk Assessment, 2015, 29(5):1-26.

[11] YUAN Conggui, ZHANG Xinzheng, XU Shuqiong. Partial mutual information for input selection of time series prediction[C]// Northeastern University. Proceedings of the 2011 Chinese Control and Decision Conference. New York: IEEE, 2011: 2010-2014.

[12] 吴中如. 大坝与坝基安全监控理论和方法及其应用[J]. 江苏科技信息, 2005(12):1-6. (WU Zhongru. Dam and dam foundation safety monitoring theory and method and its application [J]. Jiangsu Science and Technology Information, 2005(12):1-6. (in Chinese))

[13] SKLAR M.Fonctions de répartition à n dimensions et leurs marges [M]. Paris: Université Paris, 1959.

[14] 赵婷. Copula理论及其在金融分析上的应用[D]. 长沙：湖南大学, 2011.

[15] GRAY R M. Entropy and information theory [M]. New York: Springer Science & Business Media, 2011.

[16] 郭生练, 闫宝伟, 肖义, 等. Copula函数在多变量水文分析计算中的应用及研究进展[J]. 水文, 2008, 28(3):1-7. (GUO Shenglian, YAN Baowei, XIAO Yi, et al. Multivariate hydrological analysis and estimation [J]. Journal of China Hydrology, 2008, 28(3):1-7. (in Chinese))

[17] 赵慧. 基于K-S检验copula分布估计算法中边缘分布的研究[D]. 太原：太原科技大学, 2013.

[18] 吴庆波, 李再兴, 景平. 一元Cauchy分布族中两参数的分位数估计及其性质[J]. 廊坊师范学院学报(自然科学版), 2010, 10(1):8-9. (WU Qingbo, LI Zaixing, JING Ping. Quantile estimators of the two parameters in the univariate Cauchy distribution and their property [J]. Journal of Langfang Teachers College(Natural Sciences), 2010, 10(1):8-9. (in Chinese))

[19] FERNANDO T, MAIER H R, DANDY G C. Selection of input variables for data driven models: an average shifted histogram partial mutual information estimator approach [J]. Journal of Hydrology, 2009, 367(3): 165-176.

[20] MAY R J, MAIER H R, DANDY G C, et al. Non-linear variable selection for artificial neural networks using partial mutual information [J]. Environmental Modeling & Software, 2008, 23:1312-1326.

Input factor optimization study of dam seepage statistical model based on copula entropy theory

LI Xiaoqi1, 2, ZHENG Dongjian1, 2, JU Yipeng3

(1.StateKeyLaboratoryofHydrology-WaterResourcesandHydraulicEngineering,

In order to avoid the conventional method’s requirement of selecting large quantities of input factors as well as its large errors in development of a dam seepage statistical model, problems caused by the need for many items to be considered in the earlier stage of model development, the copula entropy theory combined with partial mutual information was used to optimize the input factor selection. To obtain the copula entropy, the Gumbel function was used as the copula function, the Cauchy distribution was used to replace the normal distribution, and the Hample criterion was used to select the input factors accurately. This approach was applied to seepage detection for the Nuozhadu Dam. Comparison of the present results with those obtained from the conventional factor selection approach shows that the seepage statistical model for optimizing input factor selection based on the copula entropy has a better prediction effect.

dam safety monitoring; seepage statistical model; copula entropy; input factor; partial mutual information

1000-1980(2016)04-0370-07

10.3876/j.issn.1000-1980.2016.04.015

2015-11-29

国家自然科学基金(51279052)；水文水资源与水利工程科学国家重点实验室项目(20145028312)

李小奇(1986—)，男，山东青州人，博士研究生，主要从事大坝安全监控及健康诊断研究。E-mail:lxq0920@gmail.com

TV64;TV698

A