持续强降雨引发水位耦合变化条件下堤防渗流及稳定性分析

岑威钧，李邓军，和浩楠

(河海大学水利水电学院，江苏 南京　210098)



持续强降雨引发水位耦合变化条件下堤防渗流及稳定性分析

岑威钧，李邓军，和浩楠

(河海大学水利水电学院，江苏 南京210098)

针对江、河、湖泊土质堤防工程在持续强降雨下会导致堤前水位显著变化而可能引发堤防安全隐患，采用水-气二相非饱和渗流模型对堤防进行降雨入渗和堤前水位变化耦合条件下的饱和-非饱和渗流分析。分别开展降雨入渗、堤前水位上升及持续强降雨耦合堤前水位上升过程的非稳定渗流有限元仿真分析。在此基础上对堤坡进行抗滑稳定分析，同时考察堤前水位变化及降雨过程中气相和基质吸力对堤坡稳定性的影响。计算结果表明：与单纯的降雨和水位上升相比，降雨耦合堤前水位上升会使堤身渗流及堤坡抗滑稳定性呈现较复杂的变化特性；考虑气相和基质吸力在一定程度上对堤坡稳定分析结果有利。

堤防渗流；堤坡稳定性；持续降雨；径流；水位变化；降雨耦合堤前水位上升；水-气二相流

江、河、湖泊、池塘和蓄水池等工程一般多采用土质堤防进行挡水。长时间持续强降雨会导致堤前水位快速上升。土质堤防浸水后抗剪强度一般会有较明显的下降，可能诱发堤坡失稳。持续强降雨会在地表产生超渗产流和蓄满产流[1]。强降雨来临初期，降雨强度小于地表入渗率，地表雨水完全入渗。随着降雨强度增大，堤身浅层非饱和带逐渐达到饱和或暂态饱和，迫使多余的降雨形成径流，汇于江、河、湖泊中，使堤前水位上升，并于堤坡临水处形成有压入渗[2]。对于降雨入渗、水位变化及相应的边坡稳定分析，国内外学者开展了大量有益的研究工作[1,3-7]。如刘俊新等[1]研究了非饱和地表径流-渗流和流固体耦合条件下降雨入渗对路堤边坡稳定性的影响。岑威钧等[3]对降雨条件下多裂隙膨胀岩渠坡进行了稳定性分析。孙冬梅等[4]探讨了水位下降过程中气相对土坡稳定性的影响。吴长富等[5]分析了强降雨条件下土质边坡的瞬态稳定性。Pinyol等[6]研究了库水位骤降条件下北苏格兰Glen Shira土石坝的孔隙水压力分布。Moellmann等[7]在概率框架下分析了库水位升降对土石坝坝坡稳定性的影响。已有的研究一般仅考虑降雨入渗，忽略因持续强降雨引起水位快速上升的耦合变化过程。另外，堤身浅层土体处于典型的水-气两相非饱和状态，考虑气相对非饱和土体的影响更加符合土坡真实的自然状态[8]。因此，本文基于饱和-非饱和水-气二相流理论，考虑气相和基质吸力的作用，对堤防进行非饱和非恒定渗流仿真分析，进而研究持续降雨耦合堤前水位变化条件下堤身内、外坡的抗滑稳定性变化规律。

1　地表径流与降雨入渗理论

地表径流形成过程一般可概括为降雨过程、产流过程和地面汇流过程3个阶段[2]。降雨过程是径流形成的首要环节，其大小及时空分布决定着径流的大小和变化过程。在降雨开始阶段，部分雨水首先被地表植物等截留，部分雨水降至地面。降雨量首先满足截留，其次是地表土壤的下渗和侧渗。随着降雨时间的增长，当降雨强度大于入渗率后，强降雨会使地面快速产生余水，地表洼处开始充填。待余水积满洼地后，开始产生地表径流，从高处沿坡面快速汇流至湖泊河道内，致使堤前水位快速上升。鉴于所分析堤防的降雨资料不全，本文将降雨产生的径流汇流过程进行简化，认为降雨产生的径流汇流按一定值倍比于降雨强度，并随时间变化汇于河道。

假定堤身土体中的水和气均满足达西渗流条件，依据质量守恒定律可推得水-气两相渗流的微分方程，即[8]

(1)

(2)

式中：ρg、ρw——气、水密度；kws——饱和水相渗透系数；μw、μg——水相、气相动力黏度；qg、qw——气相、水相的汇源项； Sg、Sw——气、水饱和度；Hg、Hw——气头、水头。

对堤防进行饱和-非饱和渗流分析时，需要选用合适的土水特征曲线(SWCC)模型和渗透系数模型。本文选用van Genuchten模型[9]描述土体体积含水量与基质吸力间的函数关系，其表达式为

(3)

式中：Se——饱和度；θw——体积含水量；θr——残余体积含水量；θs——饱和体积含水量； ψ——基质吸力；α、n和m为拟合参数，m=1-1/n。

相应的气相和液相闭合形式方程表示的相对渗透系数的表达式[4]为

(4)

(5)

式中：krw——水相相对渗透率；krg——气相相对渗透率；τ——迂曲度因子。

2　堤身非饱和土坡稳定性分析方法

2.1堤身饱和-非饱和土的抗剪强度

非饱和土常采用的应力状态变量是净法向应力和基质吸力。Fredlund等[9]利用这2个应力变量建立了非饱和土的抗剪强度公式：

τ=c′+(σ-ug)tanφ′+(ug-uw)tanφb

(6)

式中：(σ-ug)——净法向应力；ug——孔隙气压力；φ′——有效内摩擦角；φb——抗剪强度随基质吸力(ug-uw)增加的曲线的平均倾角。

随着降雨入渗或水位升高，堤身非饱和区域可能逐渐饱和，此时土体的孔隙气压力等于孔隙水压力，基质吸力为零，则式(6)转化为饱和土的抗剪强度公式。

2.2饱和-非饱和堤坡的抗滑安全系数

简化毕肖普法是土质边坡抗滑稳定分析中广泛应用的计算方法。在非饱和土的情况下，需要考虑基质吸力的影响，此时边坡稳定安全系数Fs的表达式[4]如下：

(7)

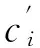
3　实例分析

3.1计算模型与计算条件

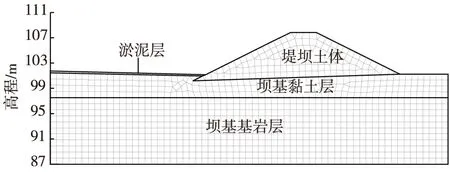
图1　有限元模型Fig. 1　Finite element model

以某一内河湖泊堤防为研究对象，计算模型如图1所示。堤防高7.3 m，堤顶宽4 m，堤顶高程为108.1 m，上、下游坡比均为1∶2，湖泊枯水位为102.25 m、丰水位为106.75 m，堤防背水侧无水。堤基黏土层厚度为4 m，黏土层以下为基岩。土体计算参数见表1。

堤身土体van Genuchten模型的参数取值[10]如下：饱和含水量θs和残余含水量θr分别取0.48和0.035，SWCC拟合参数a、n和m分别取为6.615 kPa，2.68和0.627。此外，由于淤泥、基岩和堤基黏土对堤身渗流与堤坡稳定影响相对较小，故将它们均视作饱和材料，这3种材料的饱和渗透系数见表1。

表1　堤身及地基材料参数Table 1　Material parameters of dike and foundation

选取3种典型工况进行堤身渗流与堤坡稳定对比分析。工况1模拟雨季来临时的持续强降雨，降雨在地面形成地表径流汇于湖泊中，使水位上升，其中水位上升速度随降雨过程耦合变化，模拟时间为360 h，水位最终保持在106.75 m附近；工况2模拟历时48 h的单纯降雨，其他同工况1；工况3模拟水位从枯水位102.25 m在48 h内匀速上升至106.75 m，之后保持不变，总模拟时间也为360 h。

3.2堤身非饱和非稳定渗流特性

本文主要研究强降雨与堤前水位耦合变化时的堤防渗流，鉴于考虑气相影响与不考虑气相影响条件下的渗流场变化规律基本一致，限于篇幅，仅给出考虑气相作用下的堤身渗流状态。

由于计算历时较长，选取每一定历时下的渗流浸润线变化进行分析，见图2。从图2(a)(b)可以明显看到降雨入渗于临水坡，使堤坡表层非饱和土达到暂态饱和，故而在堤坡临水面形成紧贴堤坡的浸润线。对比降雨径流导致水位升高的图2(a)与单纯水位上升的图2(c)，耦合条件下临水坡附近的浸润线变化更为复杂。

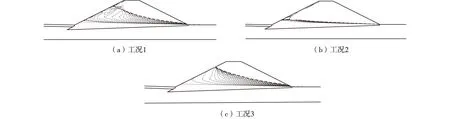
图2　各工况下浸润线的变化Fig. 2　Variations of phreatic lines in different cases

3.3堤坡抗滑稳定性

堤前水位的快速变化导致堤身浸润线变化区土体的孔隙水压力变化跟不上水位的变化，出现滞后现象，使堤防土体的受力状态变得复杂，进而影响堤坡的稳定性。为此，在饱和-非饱和渗流分析的基础上分别对考虑气相影响、不考虑气相影响和不考虑基质吸力各种条件下进行堤防的稳定性计算，求得的堤坡稳定安全系数随时间变化曲线见图3～6。

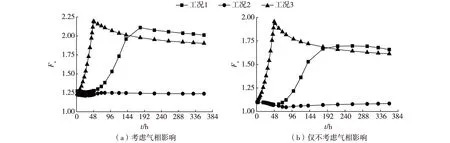
图3　各工况下堤坡稳定安全系数随时间的变化Fig. 3　Variations of safety factor of dike slope with time in different cases

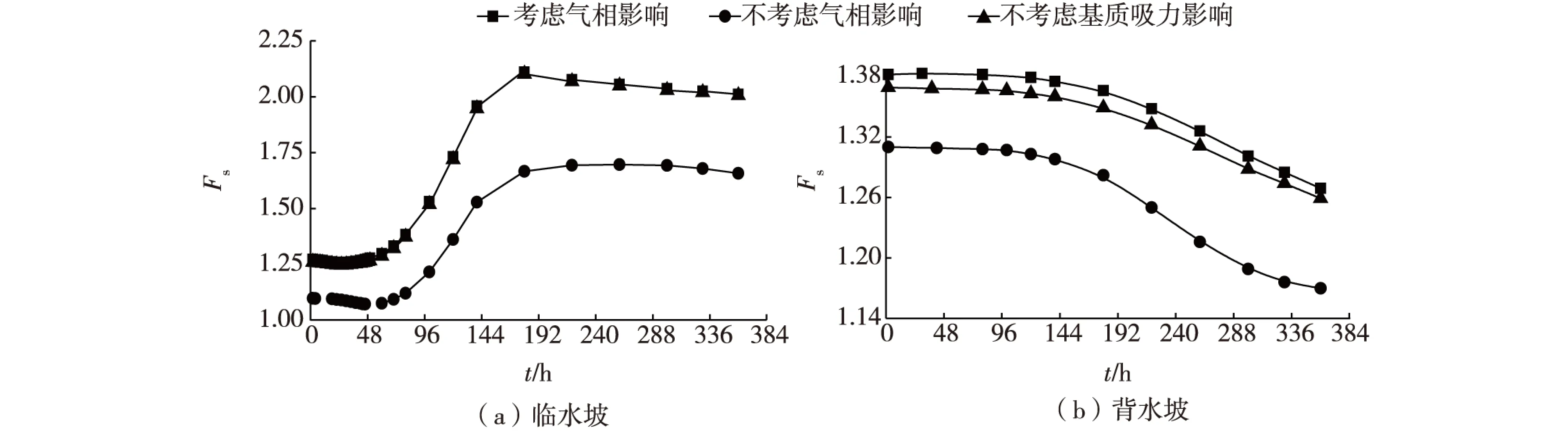
图4　工况1堤坡稳定安全系数随时间的变化Fig. 4　Variations of safety factor of dike slope with time in case 1

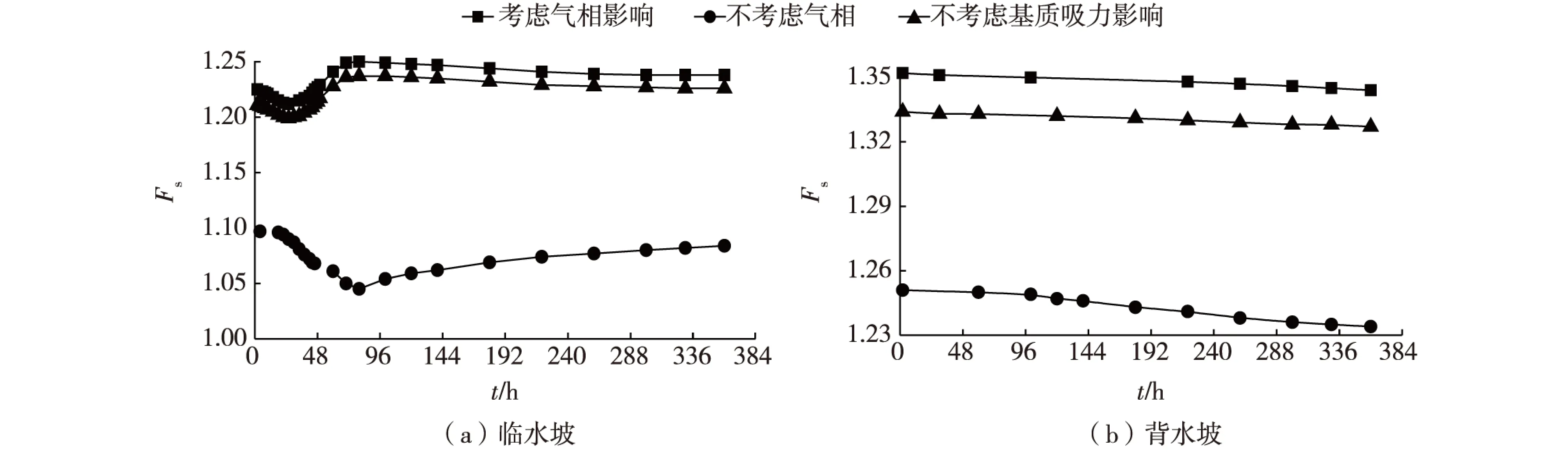
图5　工况2堤坡稳定安全系数随时间的变化Fig. 5　Variations of safety factor of dike slope with time in case 2

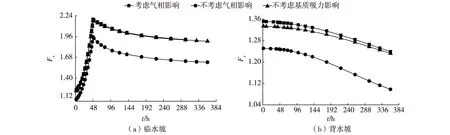
图6　工况3堤坡安全系数随时间的变化Fig. 6　Variations of safety factor of dike slope with time in case 3

由图3可见，堤前水位快速上升使堤坡抗滑力减小，但下滑力也减小，浅表土层浸水后堤坡稳定性随水位总体上呈先上升、后下降的趋势。其中，工况1为强降雨耦合堤前水位上升。降雨初期，雨水入渗，降雨产生的径流对水位的影响微小，降雨对堤坡稳定占主要因素，堤坡浸水部分土体抗滑力下降程度大于下滑力的下降，使堤坡稳定性在初期有一定的下降。这点与单纯的水位上升情况(工况3)不同。当降雨持续一定时间后，堤前水位才会因降雨径流有明显的快速上升现象，此时土体下滑力下降程度超过了抗滑力的下降程度，因而堤坡稳定安全系数有短时的快速上升。相比于单纯的水位上升情况(工况3)，此阶段堤坡稳定安全系数的上升有明显的滞后现象，且上升幅度相对缓慢些。当堤前水位到达丰水位后不再上升时，堤身内部浸润线随着时间延长会继续上升，导致堤坡的稳定性呈现缓慢下降，最终随着稳定渗流状态的到来堤坡抗滑稳定安全系数趋于稳定值。工况3模拟单纯的堤前水位急剧上升，由于一开始雨水来不及入渗堤坡，因此堤坡稳定性呈现单调上升趋势，等升到丰水位后呈现与工况1类似的情况，堤坡稳定性略有缓慢下降，表明此时河水已经慢慢入渗至堤身内，安全系数最终随渗流变化一同趋于稳定值。工况2是模拟单纯的降雨情况，相比之下，堤坡稳定安全系数变化明显平缓许多。可见，堤前水位的急剧变化较单纯降雨入渗会更明显地影响堤身的抗滑稳定性，应引起重视，尤其是两种出现耦合的情况。

由式(6)可知，非饱和土中的气相和基质吸力均对土体强度有贡献，进而影响堤坡抗滑稳定安全系数。图4～6为各工况下堤坡抗滑稳定安全系数变化过程线。工况1(图4)下，堤身临水坡稳定性在降雨初期先减小，之后随降雨引发的水位上升而增大，最终逐渐减小并趋于稳定。堤防背水坡稳定性则逐渐减小，也需引起重视。工况2(图5)下，单纯的降雨会降低堤坡稳定性。随着堤身稳定渗流场的形成，堤坡稳定安全系数有小幅度变化。工况3(图6)下，堤防临水坡稳定性因水位骤升而急剧增大，之后随河水的入渗逐渐减小，最终趋于稳定。背水坡的稳定性则单调持续减小。3种不同工况下，考虑气相和基质吸力均能提高堤坡的抗滑稳定安全系数计算值，其中气相对堤坡稳定的贡献更明显。

4　结　　论

a. 仅考虑降雨影响而不计堤前水位耦合变化时，降雨会在堤身浅层非饱和区域形成暂态饱和区，降低了浅层土体的抗剪强度，从而降低堤坡的稳定性。

b. 堤前水位急剧变化会引起堤坡稳定安全系数的急剧变化，其比降雨的影响更为显著，应引起重视。

c. 与单纯的降雨和水位骤升相比，降雨耦合堤前水位快速上升会使堤坡抗滑稳定性呈现更为复杂的变化特性，更能体现堤防的实际工作性态。

d. 考虑气相和基质吸力能使非饱和堤坡抗滑稳定安全系数计算值有所提高。

[1] 刘俊新, 刘育田, 胡启军. 非饱和地表径流-渗流和流固体耦合条件下降雨入渗对路堤边坡稳定性研究[J].岩土力学,2010,31(3):903-910.(LIU Junxin, LIU Yutian, Hu Qijun. Stability of embankment slope subjected to rainfall infiltration considering both runoff-underground seepage and fluid-solid coupling [J]. Rock and Soil Mechanics, 2010, 31(3): 903-910. (in Chinese))

[2] 任伯帜. 城市设计暴雨及雨水径流计算模型研究[D].重庆：重庆大学,2004.

[3] 岑威钧, 王蒙, 石从浩, 等. 降雨条件下多裂隙膨胀岩渠坡稳定性分析[J].郑州大学学报(工学版)，2014,35(2):10-14.(CEN Weijun，WANG Meng，SHI Conghao，et al. Stability study of an expensive channel slope with fissures due to rainfall infiltration[J]. Journal of Zhengzhou University ( Engineering Science) 2014,35(2):10-14. (in Chinese))

[4] 孙冬梅,张杨, SEMPRICH S,等. 水位下降过程中气相对土坡稳定性的影响[J]. 地下空间与工程学报,2015,11(2):511-518.( SUN Dongmei, ZHANG Yang, SEMPRICH S, et al. Effects of pore air on the stability of soil slope during the process of water level drawdown[J]. Chinese Journal of Underground Space and Engineering, 2015, 11(2):511-518. (in Chinese))

[5] 吴长富, 朱向荣, 尹小涛,等. 强降雨条件下土质边坡瞬态稳定性分析[J].岩土力学,2008, 29(2):386-391.( WU Changfu, ZHU Xiangrong, YIN Xiaotao, et al. Analysis of soil slope’s transient stability under intensive rainfall[J]. Rock and Soil Mechanics, 2008, 29(2):386-391. (in Chinese))

[6] PINYOL N M, ALONSO E E, SEBASTIO. Rapid drawdown in slopes and embankments[J]. Water Resources Research, 2008, 44(5):303-312.

[7] MOELLMANN A, VERMEER P A, HUBER M. A probabilistic finite element analysis of embankment stability under transient seepage conditions[J]. Georisk Assessment & Management of Risk for Engineered Systems & Geohazards, 2011, 5(2):110-119.

[8] FREDLUND D G, RAHARDJO H. Soil mechanics for unsaturated soils[M].New York: Wiley, 1993.

[9] GENUCHTEN M T V. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Journal of the Soil Science Society ofAmerica, 1980, 44(5):892-898.

[10] CHO S E. Probabilistic analysis of seepage that considers the spatial variability of permeability for an embankment on soil foundation[J]. Engineering Geology, 2012, 133/134(3):30-39.

Analysis of dike seepage and slope stability under coupled conditions of continuously heavy rainfall and consequent change of water level

CEN Weijun, LI Dengjun, HE Haonan

(CollegeofWaterConservancyandHydropowerEngineering,HohaiUniversity,Nanjing210098,China)

In dike engineering projects for rivers and lakes, continuously heavy rainfall will lead to a significant change in the water level, which may cause safety hazards to dikes. To solve these problems, a water-gas two-phase unsaturated seepage model was used to analyze the saturated-unsaturated seepage of a dike under the coupled conditions of rainfall infiltration and water level change. Finite element simulation was performed to study the unsteady seepage in the processes of rainfall infiltration, water level rise in front of the dike, and coupling of continuously heavy rainfall and the water level rise. On these bases, anti-sliding stability analysis of the dike slope was conducted, with consideration of the effects of the dike water level changes, and the gas phase and matric suction during rainfall on the slope stability. The results show that, compared to the rainfall infiltration or the water level rise, the coupled conditions of rainfall and the water level rise will cause the seepage and slope stability of the dike to become more complex. Considering the gas phase and matrix suction will be helpful to slope stability analysis.

dike seepage; slope stability of dike; continuous rainfall; runoff; water level change; coupling of rainfall and water level rise; water-gas two-phase flow

1000-1980(2016)04-0364-06

10.3876/j.issn.1000-1980.2016.04.014

2015-12-10

江苏省自然科学基金(BK20141418);江苏高校优势学科建设工程项目(YS11001)

岑威钧(1977—)，男，浙江慈溪人，副教授，主要从事水工渗流分析与控制及土石坝抗震研究。E-mail:hhucwj@163.com

TU431

A