基于尖点突变理论的路堤填筑下伏溶洞顶板稳定性研究

何忠明，刘森峙，胡庆国，刘清芳(1.长沙理工大学 特殊环境道路工程湖南省重点实验室，湖南 长沙，410114；2.广西交通投资集团有限公司，广西 南宁，50022；.长沙理工大学 交通运输工程学院，湖南 长沙，410114)

基于尖点突变理论的路堤填筑下伏溶洞顶板稳定性研究

何忠明1,2,3，刘森峙3，胡庆国3，刘清芳3
(1.长沙理工大学 特殊环境道路工程湖南省重点实验室，湖南 长沙，410114；
2.广西交通投资集团有限公司，广西 南宁，530022；
3.长沙理工大学 交通运输工程学院，湖南 长沙，410114)

为了分析路堤填筑过程中下伏溶洞顶板稳定性，基于尖点突变理论建立稳定性判定的数学模型；以湖南省益娄(益阳—娄底)高速公路岩溶路段地质条件为研究背景，基于上述稳定性判定模型，设计不同厚度的溶洞顶板填筑时的工况，采用FLAC3D软件模拟分析每层路堤填筑时的顶板稳定性变化规律。研究结果表明：随着路堤填筑高度增加，顶板会逐渐发生失稳变形，顶板厚度与路堤极限填筑高度之间呈二次函数关系；当路堤填筑高度超过极限填筑高度时，上部黏土层与顶板的沉降等值线连通，沉降值最大区域从黏土层移动至顶板中部，塑性区向上延伸发展至地表贯通，对路堤建设产生危害。

尖点突变理论；溶洞；路堤填筑；顶板稳定性；极限填筑高度

随着公路建设的发展，在岩溶地区修筑高速公路较常见。在岩溶地区的公路建设中，需要特别考虑路堤填筑的施工过程对溶洞顶板稳定性的影响。天然溶洞或人工洞室顶板不稳定现象，会逐渐向上延伸破坏最终使得地表塌陷，对建筑环境会造成潜在危害[1]。溶洞顶板作为基础的持力层，其稳定性与溶洞顶板厚度、围岩特性、岩溶发育程度、基础尺寸、顶板跨度以及工作荷载等多种因素密切相关[2-3]。近年来，国内外不少学者[1,4-7]对于建筑物下方溶洞顶板稳定性的评价以及安全厚度的确定，逐渐由传统的定性方法发展为半定量及定量方法。由于溶洞顶板具有非线性失稳破坏的特性，大量学者采用突变理论探讨路基溶洞顶板的稳定性，得到了较合理的结论[8-9]。但现阶段对溶洞稳定性方面的研究较侧重于路基溶洞顶板稳定性影响因素的分析[10]、顶板安全厚度的确定[5-8]以及采用强度折减法[7,9-12]探讨安全系数，而对于路堤填筑过程及填筑高度对隐伏溶洞顶板稳定性影响的研究较少。为此，本文作者根据极限平衡的思想，基于尖点突变理论建立路堤填筑过程中溶洞顶板失稳判定的数学模型，探讨不同溶洞顶板厚度下路堤填筑过程中顶板稳定性及其极限填筑高度，以便为工程实践提供参考。

1　溶洞顶板稳定性判定数学模型的建立

1.1顶板极限平衡状态判据及极限填筑高度确定

溶洞顶板的受力状态可简化为受致塌力(如岩土体的自重和外界荷载，以F表示)以及抵抗力(由岩土体自身强度决定，以f表示)两者共同的作用；溶洞的稳定状态由致塌力和抵抗力两者之间的比值决定。

在岩溶区，溶洞上方路堤填筑施工前，溶洞处于稳定状态，随着路堤填筑高度的不断增加，溶洞所受的致塌力不断加大，溶洞顶板从稳定状态向非稳定状态发展。当F=f时，顶板处于极限平衡状态，此时，溶洞上方路堤的填筑高度为极限填筑高度，设为[H]。路基溶洞顶板的受力状态较复杂，极限平衡状态的判据也较困难。路基溶洞的沉降变形会随路堤填筑高度的增加而增大，可以对溶洞顶板最易发生沉降的部位设置监测点，分析沉降刚要发生突变时的状态，以此作为路堤填筑下伏溶洞顶板极限平衡状态的判据是较可取的方法。因此，本文作者建立溶洞顶板中点的竖向沉降Z随溶洞上方路堤填筑高度h的数学函数关系式Z(h)，再将其转化为尖点突变模型的势函数，计算分叉集值来确定溶洞顶板的极限平衡状态。

记录每层填筑的路堤荷载p作用下的溶洞顶板中点竖向沉降Z，将二者拟合为泰勒级数形式的关系曲线。为获得尖点突变势函数的标准形式，截取至函数4次项：

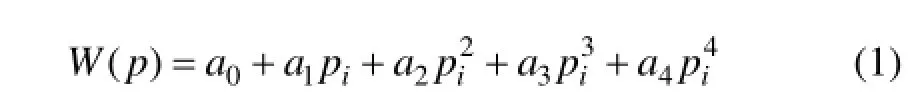
式中：a0，a1，a2，a3和a4均为不确定系数；p=γh；γ为路堤填土的容重，kN/m3；h为填筑高度，m。故式(1)可转化为

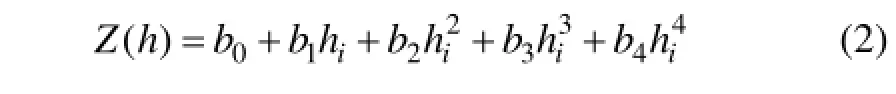
式(2)可参考文献[9]和[12]中方法进行变换：令hi=m-n，n=b3/(4b4)，则式(2)可通过矩阵

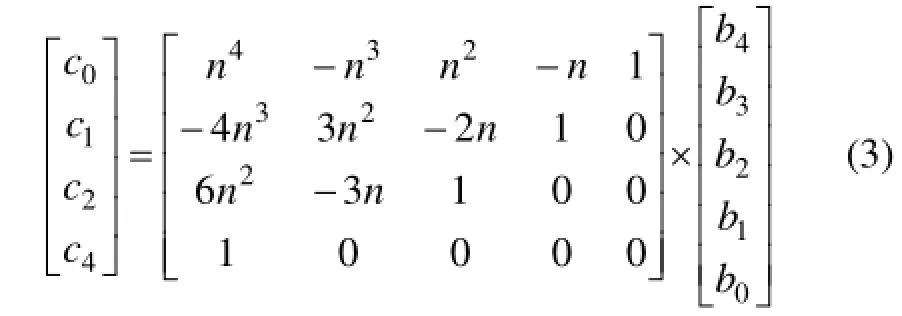
化为

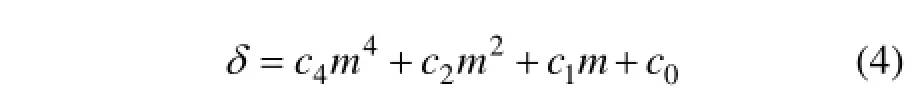
对式(4)进一步化简得

式中：

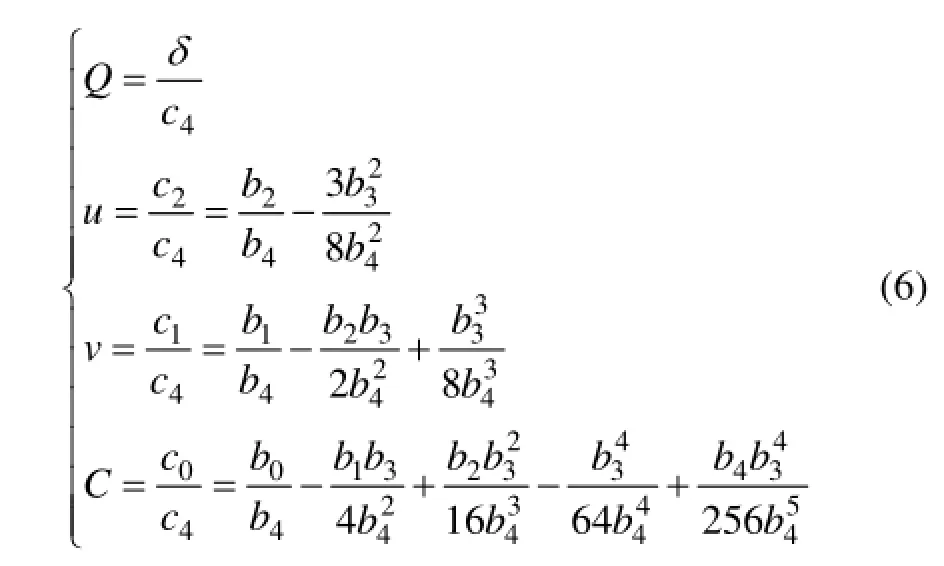
分别对式(5)求一阶导数和二阶导数得：

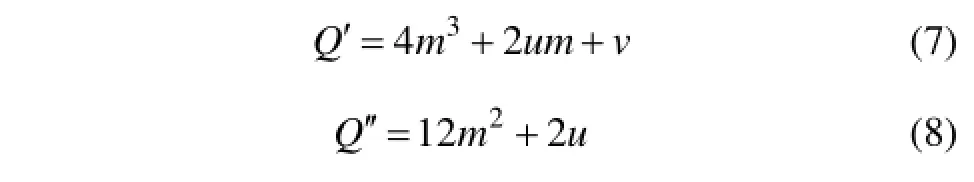
式(7)与(8)均与系数C无关，故可根据以上各式的推导，确定溶洞上方路堤填筑的尖点突变理论标准势函数模型为

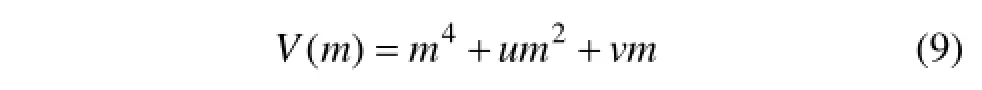
在路堤填筑溶洞顶板的系统中，该系统的状态由控制变量u和v以及状态变量m确定。在由(m，u，v)所构成的三维状态空间中(如图1所示)，平衡曲面M为所有平衡点的集合，平衡点应满足

M在(m，u，v)空间中为1个具有褶皱的光滑曲面，具有突跳、双模态、滞后、发散及不可达等特征[13]。对于突变点应满足：

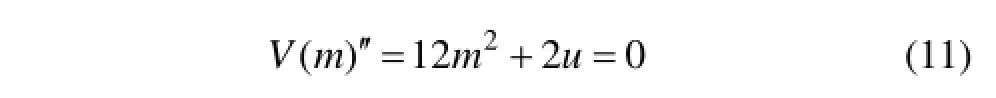
它们在控制变量u-v平面的投影就构成分叉集Δ。联立式(10)和式(11)消去m可得

平衡曲面的空间图形由上叶、中叶和下叶构成，当系统控制变量u和v位于交叉集外区域即Δ＞0时，相应的平衡曲面空间点在曲面的上叶或下叶平衡变化，溶洞顶板稳定；当Δ＜0时，空间点位于中叶，中叶是不稳定的，故系统处于不稳定状态，岩溶顶板发生塌陷；当Δ=0时，空间点位于中叶或上叶边缘，相应点即将发生突跳，故此时系统处于临界稳定状态也就是极限平衡状态，同时确定路堤的极限填筑高度[H]。

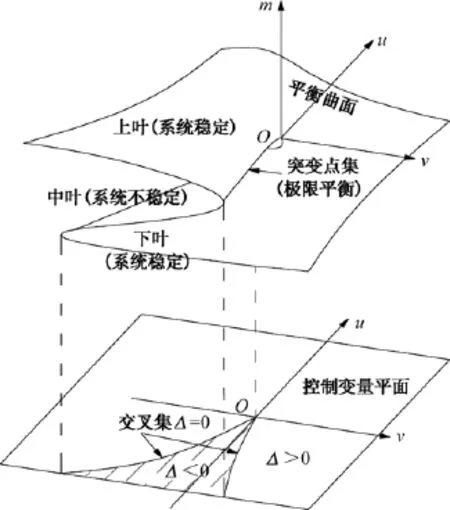
图1　尖点突变模型示意图Fig.1　Model of cusp catastrophe

1.2路堤填筑下伏溶洞顶板稳定性判定的过程

在本文中，对于溶洞顶板稳定性的研究，采用Mohr-Coulomb模型，并假设溶洞顶板岩体完整，且能产生大变形。Mohr-Coulomb破坏准则的表达式为[14]

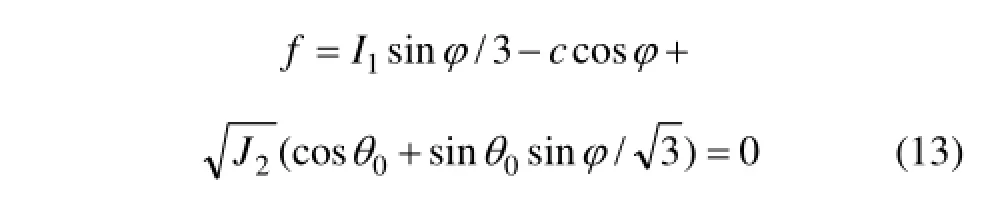
式中：I1和J2为应力张量第 1不变量和应力偏量第 2不变量；θ0为应力罗德角；c和φ分别为黏聚力和内摩擦角。基于尖点突变理论的路堤填筑下伏溶洞顶板稳定性判定过程为：先利用FLAC3D软件建立溶洞几何模型并划分网格，进行初始应力平衡，设置路堤填筑前的初始应力条件；采用Mohr-Coulomb模型进行弹塑性求解至收敛；模拟溶洞上方路堤逐层填筑的过程，记录各层填筑高度hi下洞顶中点的沉降zi，并分别将hi填筑高度及其之前记录的所有的(h,z)数据点进行4次函数的曲线拟合，设为Z(h)i；将函数变换为突变数学模型，计算交叉集的值，对溶洞顶板系统的稳定性进行判定，从而确定路堤极限填筑高度。

需说明的是：本文对路堤填筑的模拟，每层填筑增加的高度都相等，因此，在分析过程中，当确定某一层填筑后系统为稳定，而下一层填筑后为不稳定，将默认该层路堤填筑后的系统状态为极限平衡状态。具体判定过程如图2所示。

1.3稳定性判定的可靠性验证

为验证数学模型判定的可靠性，在本文中利用有限差分数值分析软件FLAC3D对郑颖人等[11]作过的隧洞模型实验进行模拟。由于本文讨论溶洞顶板稳定性，故选取文献[11]中的浅埋隧洞模型，其尺寸及力学参数均不变，材料采用Mohr-Coulomb本构模型。FLAC3D软件对整个模型共划分5 360个单元，对隧洞周围单元划分较密，其他区域依次变疏，模型的几何形状以及网格划分结果如图3所示。

室内模拟试验的过程是对模型逐级增加荷载，并记录每级荷载下模型洞顶中点的竖直沉降。顶板沉降位移发展趋势如图4所示，沉降位移随荷载逐级增加而增大，当荷载超过25 kN时，沉降趋势明显，此时可将各监测点之前所有数据点进行曲线拟合。表1所示为荷载高于27 kN时部分拟合曲线的函数关系式，各曲线的拟合系数R2均大于0.96，故各拟合曲线能反映系统的沉降位移趋势。从表1可知：当荷载≤27.24 kN时，尖点突变模型的交叉集Δ大于0，判定隧洞模型的顶板未破坏；当荷载≥27.30 kN时，Δ小于0，可以判定隧洞模型顶板已经发生破坏，由此可以确定模型隧洞的极限荷载为27.24~27.30 kN，由于两者相差不大，极限荷载默认为27.24 kN。选取文献[11]中室内模型试验的破坏状态与27.24 kN下的数值模拟塑性区云图进行对比(见图5)，可知二者的破坏模式较一致，且数值计算得到的极限荷载为27.24 kN，与室内试验的28 kN接近，由此说明采用尖点突变的数学模型判定路堤填筑荷载下溶洞顶板稳定性是合理、可靠的。

图2　判定过程流程图Fig.2　Flow chart of determination process

图3　数值模拟的有限差分网格Fig.3　Finite difference grids of numerical simulation

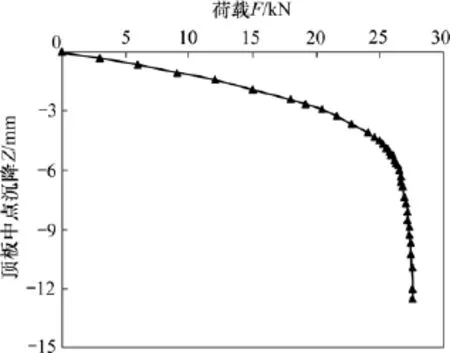
图4　荷载-顶板沉降曲线Fig.4　Relationship between loads and displacements of roof

图5　模型实验的破坏状态[11]与数值分析的塑性区云图Fig.5　Failure situation of model test[11]and plastic zone of numerical simulation

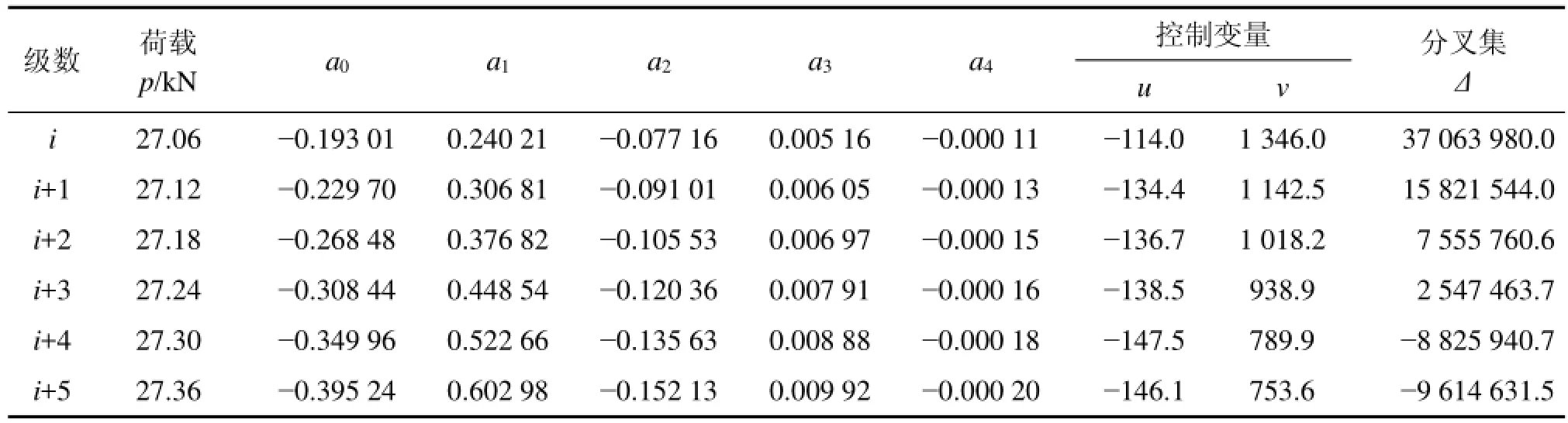
表1　各荷载下的位移拟合曲线、尖点突变模型控制变量及ΔTable 1　Displacements fitting curves,control variables and Δ of cusp catastrophe models under different loads

2　数值模型建立

2.1工程概况及计算模型

湖南省益娄高速公路沿线多个路段岩溶发育，部分路段勘测出有大型溶洞，溶洞的形状接近椭球形，并埋藏于土层下方。溶洞围岩属微风化岩，上层依次覆盖有坡积黏土和粉质黏土。为简化分析最易发生塌陷地段，本文截取其中一溶洞横断面最大路段，取道路行车方向长度1 m，并假设填筑的路堤位于溶洞的正上方。

采用FLAC3D软件建立如图6所示的数值计算模型，模型长×宽×高为60 m×1 m×36 m，溶洞位于模型正中部，椭圆形溶洞的长轴为12 m，短轴为6 m，溶洞顶板厚度为2 m，上层覆盖的坡积黏土及粉质黏土的厚度分别为4 m和2 m。模型各岩土地层的力学参数如表2所示。

对于计算模型的边界条件设置为：模型的两侧均为水平方向位移约束，模型底部为水平和竖直方向位移约束，模型顶部为自由界，整个模型的行车方向位移约束。

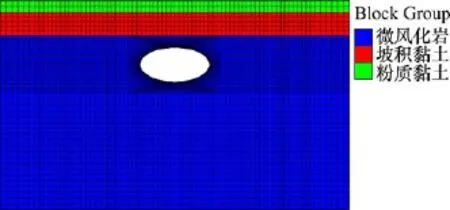
图6　计算模型Fig.6　Numerical model

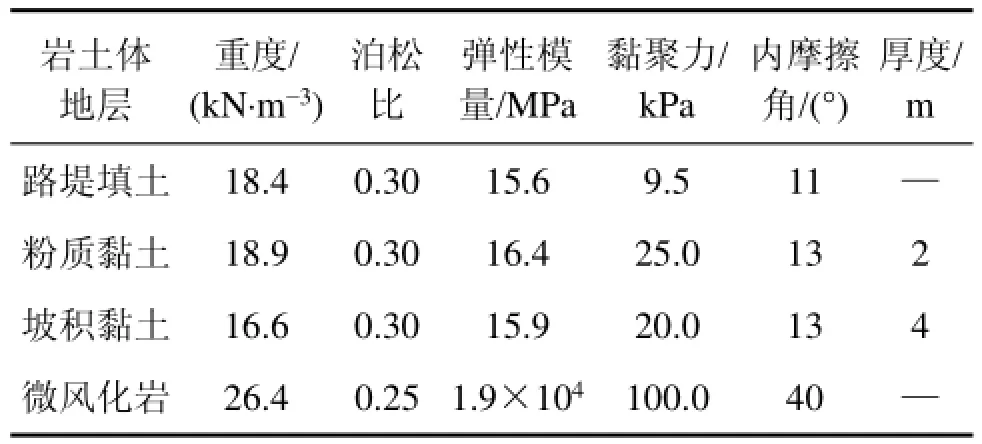
表2　岩土体力学参数Table 2　Mechanical parameters of geotechnical

2.2路堤填筑过程模拟

根据公路路基设计规范(JTG D30—2015)[15]，路堤施工应进行分层铺筑。本文采用FLAC3D中的apply命令施加应力来代替路堤填土的填筑，路堤荷载的应力hγσ=，应力分布采用gradient命令模拟路堤梯形应力的分布；为模拟路堤每层压实后的填筑，每级应力的增加相当路堤填筑高度增加20 cm，路堤填筑高度增加时保持路基宽度(包括路肩、行车道和中间道)26 m[16]不变以及路堤边坡坡率1:1.5不变，以此确定极限填筑高度时的路堤横断面形式。为简化分析，在本文中未考虑行车荷载和其他外界条件的影响，且假设路堤填土为均质土，路堤填筑仅考虑溶洞顶板的沉降位移，不考虑路堤的变形作用。

3　结果分析

3.1路堤填筑不同厚度的下伏溶洞顶板稳定性

采用上述的模拟过程和方法探讨顶板厚度为2 m的工况下路堤填筑过程中溶洞顶板的稳定性，得到各填筑高度下顶板系统控制变量和分叉集的值，从而分析顶板的稳定状态，结果如表3所示。

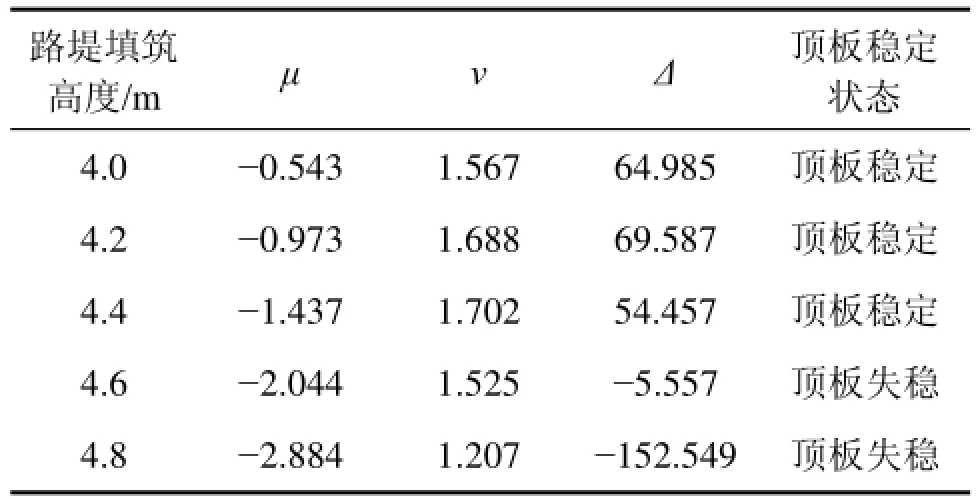
表3　路堤填筑过程中顶板稳定状态Table 3　Stability of roof in process of embankment filling

由表3可知：在路堤填筑高度为4.4 m时，系统分叉集Δ大于0，可判定顶板未失稳破坏；当填筑高度达到4.6 m时，溶洞顶板中点的沉降位移达130 mm，且Δ小于0，系统产生突变，顶板失稳。因此，可以确定2.0 m厚溶洞顶板上方路堤的极限填筑高度为4.4 m。在实际工程中，考虑到车辆荷载和其他外界环境的影响，路堤填筑高度应不超过4 m。

通过大量试算和判定，确定了顶板厚度为1.5，2.0，2.5，3.0和3.5 m各工况下，极限填筑高度分别为2.2，4.4，7.2，9.8和14.2 m，二者关系如图7所示。从图7可见：随着顶板厚度增加，路堤填筑的极限高度增加。经多次拟合，二者的关系最符合二次函数关系，拟合系数R2=0.997。分析得知各厚度顶板上路堤的填筑高度超过极限填筑高度时，溶洞顶板将产生失稳破坏。

3.2路堤填筑下伏溶洞顶板沉降趋势分析

当顶板厚度为2 m，路堤高度为2.0，3.0和4.4 m时的溶洞顶板沉降分布见图8。由图8可见：在路堤高度未达到极限填筑高度时，顶板的沉降不大，路基沉降最大的区域位于顶板正上方的黏土层。这是由于上方路堤荷载未超过顶板的强度，路堤的填筑使顶板产生的沉降变形不大，而顶板以上黏土层的模量较小，在路堤荷载下产生压缩变形。随着路堤高度达到极限填筑高度，最大沉降区域由黏土层移动至顶板中心，最大沉降达到93 mm，沉降将产生突变，并且溶洞顶板与黏土层的沉降等值线连通，顶板将会发生失稳破坏。

图7　顶板厚度与极限填筑高度关系Fig.7　Relationship between thickness of roof and ultimate filling height

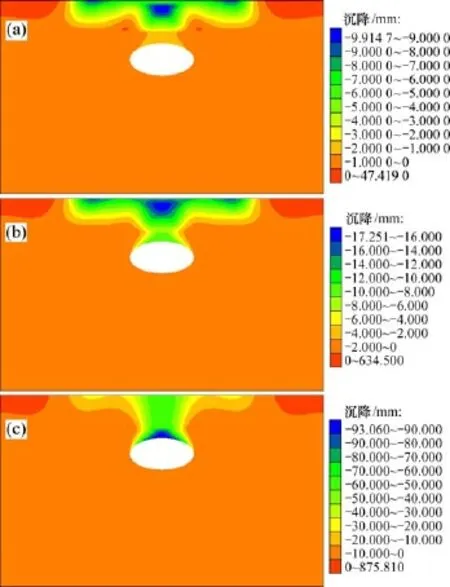
图8　沉降分布Fig.8　Vertical displacement distributions

3.3路堤填筑下伏溶洞顶板的塑性区分布

图9所示为在路堤填筑过程中(顶板厚度为2 m)，填筑高度逐渐达到和超过极限填筑高度下的模型塑性区分布。从图9可知：在路堤高度为2 m时，顶板受到上部土层和路堤的荷载作用，已经开始产生塑性区，与一般的水平顶板不同，椭圆溶洞的拱形顶板具有一定的应力传递效应，使得顶板两侧所受的应力也较大；顶板上部及两侧区域主要产生拉伸破坏和剪切破坏，而上层土体的塑性区面积较小，对上方建筑物的稳定影响不大；当填筑高度为3 m时，塑性区发展开始向上延伸，并在黏土层与岩层界面处产生一定的剪切破坏。对比路堤高度为4.4 m和4.6 m下的塑性区可知，当路堤超过极限填筑高度时，溶洞上方的塑性区向地表处延伸并贯通，顶板的失稳破坏将对路堤建设造成较大危害。

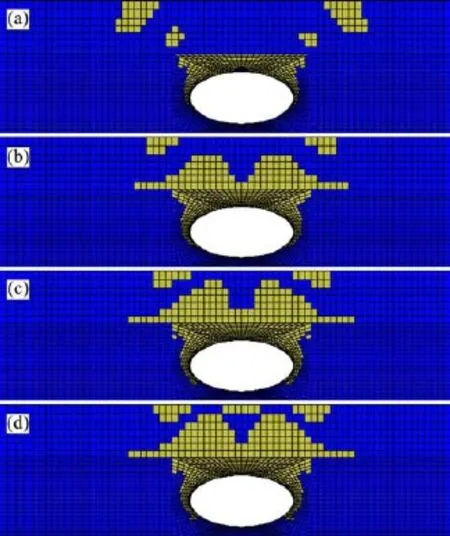
图9　塑性区分布Fig.9　Plastic zone distributions

4　结论

1)建立了路堤填筑过程中溶洞顶板稳定性判定的尖点突变理论数学模型，验证了该方法对溶洞顶板稳定性判定的可靠性，是一种较合理的定量分析方法。

2)以湖南省益娄高速公路的岩溶路段地质条件为例，确定了溶洞顶板厚度分别为1.5，2.0，2.5，3.0 和3.5 m工况时，路堤的极限填筑高度分别为2.2，4.4，7.2，9.8和14.2 m，顶板厚度与极限填筑高度之间较符合二次函数关系。

3)在未处治的情况下，当溶洞上方的路堤填方高度超过极限填筑高度时，溶洞顶板的失稳破坏将延伸至上方地表，对路堤建设造成较大危害。

[1]PARISE M,LOLLINO P.A preliminary analysis of failure mechanisms in karst and man-make underground caves in Southern Italy[J].Geomorphology,2011,134(1/2):132-143.

[2]阳军生,张军,张起森,等.溶洞上方圆形基础地基极限承载力有限元分析[J].岩石力学与工程学报,2005,24(2):296-301. YANG Junsheng,ZHANG Jun,ZHANG Qisen,et al.Finite element analysis of ultimate bearing capacity of circular footing above karst cave[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(2):296-301.

[3]胡庆国,张可能,阳军生.溶洞上方条形基础地基极限承载力有限元分析[J].中南大学学报(自然科学版),2005,36(4): 694-697. HU Qingguo,ZHANG Keneng,YANG Junsheng.Finite element analysis of ultimate bearing capacity of strip footing above karst cave[J].Journal of Central South University(Science and Technology),2005,36(4):694-697.

[4]韩红艳,吴燕舞,黑亮,等.岩溶路基溶洞顶板稳定性分析[J].工程地质学报,2012,20(6):1078-1082. HAN Hongyan,WU Yanwu,HEI Liang,et al.Stability analysis of karst cave roof beneath highway subgrade[J].Journal of Engineering Geology,2012,20(6):1078-1082.

[5]HATZOR Y H,WAINSHTEIN I,MAZOR D B.Stability of shallow karstic caverns in blocky rock masses[J].International Journal of Rock Mechanics&Mining Sciences,2010,47(8): 1289-1303.

[6]JIANG Chong,LIU Lang,WU Junping.A new method determining safe thickness of karst cave roof under pile tip[J]. Journal of Central South University,2014,21(3):1190-1196.

[7]曹文贵,程晔,赵明华.公路路基岩溶顶板安全厚度确定的数值流形方法研究[J].岩土工程学报,2005,27(6):621-625. CAO Wengui,CHENG Ye,ZHAO Minghua.Studies on numerical manifold method for determination of safe thickness of karst roof in roadbed[J].Chinese Journal of Geotechnical Engineering,2005,27(6):621-625.

[8]张建华.基于突变理论的岩溶区路基顶板安全厚度分析[J].铁道科学与工程学报,2009,6(3):52-55. ZHANG Jianhua.Analysis of cave roof safe thickness in karst region based on catastrophe theory[J].Journal of Railway Science and Engineering,2009,6(3):52-55.

[9]ZHAO Yanlin,PENG Qingyang,WAN Wen,et al.Fluid-soild coupling analysis of rock pillar stability for concealed karst cave ahead of a roadway based on catastrophe theory[J].International Journal of Mining Science and Technology,2014,24(6): 737-745.

[10]蒋冲,赵明华,胡伯学,等.路基溶洞顶板稳定性影响因素分析[J].公路工程,2009,31(1):5-9. JIANG Chong,ZHAO Minghua,HU Boxue,et al.Stability factors analysis for subgrade karst roof[J].Highway Engineering, 2009,31(1):5-9.

[11]郑颖人,徐浩,王成,等.隧洞破坏机理及深浅埋分界标准[J].浙江大学学报(工学版),2010,44(10):1851-1856. ZHANG Yingren,XU Hao,WANG Cheng,et al.Failure mechanism of tunnel and dividing line standard between shallow and deep bury[J].Journal of Zhejiang University(Engineering Science),2010,44(10):1851-185.

[12]赵延林,吴启红,王卫军,等.基于突变理论的采空区重叠顶板稳定性强度折减法及其应用[J].岩石力学与工程学报, 2010,29(7):1424-1434. ZHAO Yanlin,WU Qihong,WANG Wenjun,et al.Strength reduction method to study stability of goaf overlapping roof based on catastrophe theory[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(7):1424-1434.

[13]凌复华.突变理论及其应用[M].上海:上海交通大学出版社, 1987:123-124. LINGFuhua.Catastrophetheoryanditsapplications[J]. Shanghai:Shanghai Jiaotong University Press,1987:123-124.

[14]Itasca Consulting Group.Theory and background[R].Minnesota: Itasca Consulting Group,2002.

[15]JTG D30—2015,公路路基设计规范[S]. JTG D30— 2015,Specificationsfor design of highway subgrades[S].

[16]邓学钧.路基路面工程[M].北京:人民交通出版社,2013: 62-63. DENG Xuejun.Road subgrade and pavement engineering[M]. Beijing:China Communications Press,2013:62-63.

(编辑陈灿华)

Stability of karst cave roof during embankment filling based on cusp catastrophe theory

HE Zhongming1,2,3,LIU Senzhi3,HU Qingguo3,LIU Qingfang3
(1.Key Laboratory of Special Environment Road Engineering of Hunan Province, Changsha University of Science&Technology,Changsha 410114,China;
2.Guangxi Communications Investment Group Co.Ltd,Nanning 530022,China;
3.School of Traffic and Transportation Engineering,Changsha University of Science&Technology, Changsha 410014,China)

In order to analyze the stability of karst carve roof in the process of embankment filling,a mathematical model for stability determination based on the cusp catastrophe theory was established.Based on the geological conditions of the construction section in Yi—Lou highway of Hunan Province and the above stability determination model,the working conditions of the karst cave roof with different thicknesses were designed,and the FLAC3Dsoftware was used to analyze the stability of the roof when the embankment was filled.The results show that the roof gradually exhibits instability deformation with the increase of embankment filling height,and the relationship between the height of roof thickness and the ultimate filling height of the embankment is the quadratic function.When the embankment heightexceeds the limit filling height,the displacement contours of the upper clay layer is connected with the roof,the largest area of the vertical displacement moves from the clay layer to the middle part of the roof,and the plastic zone extends up to the surface and perforating,which is harmful to the construction of the embankment.

the cusp catastrophe theory;karst cave;embankment filling;roof stability;the ultimate filling height

何忠明，博士(后)，副教授，从事道路工程的教学与研究工作；E-mail:hezhongming45@126.com

U49

A

1672-7207(2016)07-2456-07

10.11817/j.issn.1672-7207.2016.07.037

2015-11-20；

2016-01-10

国家自然科学基金资助项目(51508042)；湖南省交通运输厅科技进步与创新计划项目(201417)；长沙理工大学特殊环境道路工程湖南省重点实验室开放基金资助项目(kfj140501)；湖南省教育厅科学研究重点项目(14A007)(Project(51508042)supported by the National Natural Science Foundation of China;Project(201417)supported by Transportation Department Scientific&Technological Progress and Innovation Plan of Hunan Province;Project(kfj140501)supported by the Open Fund of Key Laboratory of Special Environment Road Engineering of Hunan Province,Changsha University of Science&Technology;Project(14A007)supported by the Research Foundation of Education Burea of Hunan Province)