矿柱流变对采空区顶板稳定性的影响

巨未来，王文杰

(1.武汉科技大学资源与环境工程学院，湖北 武汉 430081；2.冶金矿产资源高效利用与造块湖北省重点实验室，湖北 武汉 430081)

0 引 言

为保障因地下开采所形成采空区的安全，生产矿山往往留有一定规模的保安矿柱或采区间柱[1-2]，采空区顶板在矿柱支撑作用下将保持一段时期的稳定。但随着时间推移，采空区矿柱因自身流变、地下水侵蚀、爆破振动等因素影响，自身岩体强度大幅降低，易导致采空区顶板-矿柱体系局部破裂直至坍塌，造成采空区顶板冒落气浪冲击或地表塌陷等矿山安全事故[3-5]。因此，研究采空区顶板-矿柱支撑体系破坏的时效过程，预测采空区顶板-矿柱支撑体系的维稳时间，可为及时制定合理的采空区危害防治措施提供科学根据。

目前，针对采空区顶板破坏理论分析方面的研究多基于简支梁[6-7]或弹性薄板理论[8-10]，这种简化方式虽使计算简化，但由于条件的简化无法考虑到顶板的空间效应及顶板内的剪切变形，存在一定局限性。对于金属矿采空区来说，因其地质条件、赋存环境等更为复杂，致使顶板厚度h同顶板宽度w的比例一般不满足弹性薄板的要求(h/w<1/5时，称为薄板)。相较于薄板理论，中厚板理论在分析板的受力变形过程中，既考虑了拉应力的作用，同时包含了横向剪切的作用。因而应用中厚板理论来简化顶板并研究顶板的变形过程更符合实际要求。此外，大量工程实践表明，诸多岩石工程的失稳现象都与岩石流变特性有关[11]，矿体开挖形成的空区在初期阶段会保持一定稳定性，但随着时间推移，岩体在自身流变作用下发生蠕变变形，最终可能导致岩体工程的失稳破坏。基于此，本文以Reissner厚板理论构建采空区顶板矿柱力学模型，研究矿柱流变作用下顶板破坏的时效过程，分析并预测顶板维稳时间。

1 顶板-矿柱流变力学模型

基本假设：①顶板上覆岩层的自重视为均布荷载q0；②顶板近似看作矩形板；③考虑流变力学的复杂性，不考虑顶板的流变作用，顶板视为弹性厚板；④矿柱近似等距分布且数量n足够多。采空区顶板简化模型如图1所示，顶板长边为a，宽为b，板厚为h，顶板岩体弹性模量为E，泊松比为v，容重为r，顶板极限抗拉强度为[σT]。所有矿柱视为同性质同规格的黏弹性体，并用广义Kelvin体表征其本构关系，矿柱高度为H，平均横截面积为A，矿柱所承受的载荷按均布受荷处理。顶板矿柱力学简化模型见图2。

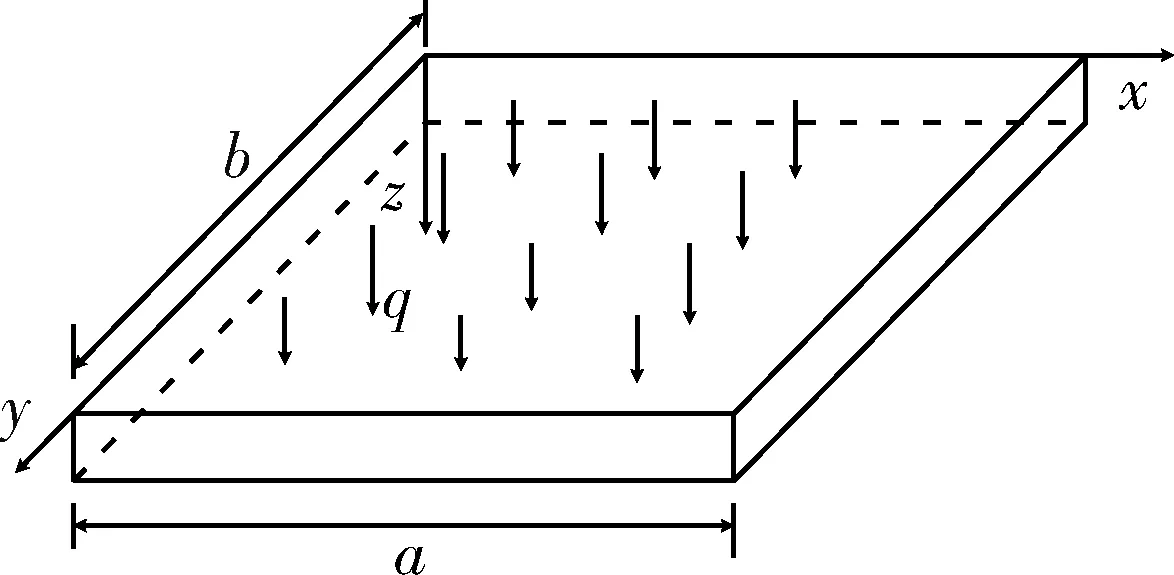
图1 顶板简化模型Fig.1 Roof simplification model

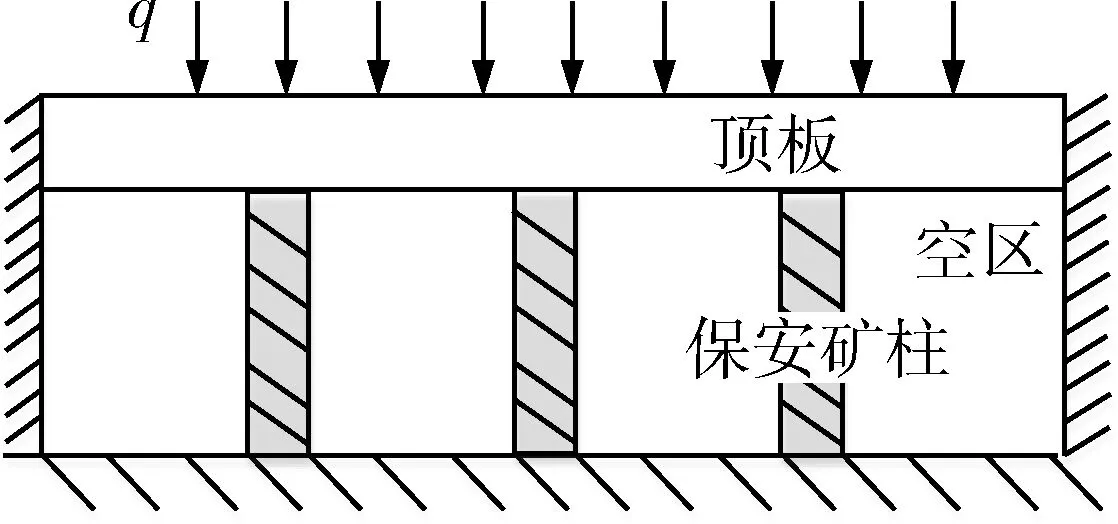
图2 简化的顶板-矿柱力学模型Fig.2 Simplified roof-pillar mechanics model

矿柱的应力应变关系用广义开尔文[12](modified Kelvin)体描述，其本构方程见式(1)。

(1)

式中：σ为矿柱应力;E1为虎克体弹性系数;E2、η分别为凯尔文体的弹性和黏性系数;dσ/dt、dε/dt分别为应力对时间的导数和应变速率。

根据Reissner厚板理论[13]，采空区顶板的控制方程见式(2)。

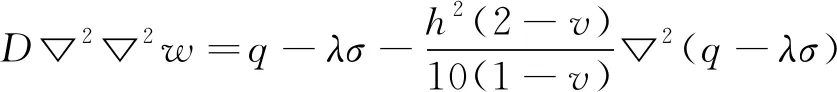
(2)

式中：D=Eh3/[12(1-v2)]，为顶板的抗弯刚度；▽2为拉普拉斯算子；w为顶板挠度函数；h为板厚；q为顶板荷载；λ为矿柱总截面与顶板面积比。

考虑到q和λσ为均匀荷载，因此将式(2)简化为式(3)。

D▽2▽2w=q-λσ

(3)

矿柱应变与变形位移的关系见式(4)。

ε=w/H

(4)

联立式(1)和式(3)可得式(5)。

(5)

式(5)为基于厚板理论的采空区顶板-矿柱系统流变微分方程。

设顶板变形下沉挠度函数为w=wtf(x,y)，wt是顶板中央最大下沉量关于流变时间的函数。采用伽辽金法求解式(5)，则得式(6)。

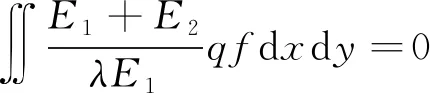
(6)

根据式(7)可将式(6)简化为式(8)。

∬f2dxdy=α1,

∬▽2▽2f2dxdy=α2,

∬fdxdy=α3

(7)

(8)

求解式(8)得式(9)。

wt=ce-n1t+n2

(9)

式中：c为积分常数，可由初始变形条件确定;n1=m2/m1;n2=m3/m2。

2 顶板失稳破坏过程计算分析

1) 当采空区顶板未发生破坏时，顶板四边都为固支，此时顶板的边界条件见式(10)。

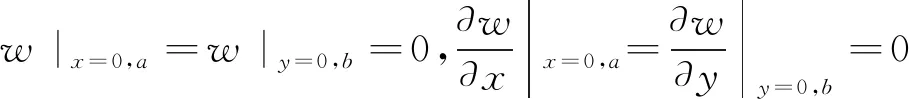
(10)

根据边界条件，当顶板四边为固支时，取挠度试函数见式(11)。

w=wtf(x,y)=

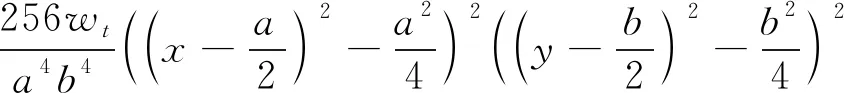
(11)

可以看出，f(x,y)满足此固支顶板所有边界条件，将式(11)带入式(7)，积分计算可得：α1=0.165ab，α2=5.944/ab+5.202(b/a3+a/b3)，α3=0.285ab。

初始阶段，矿柱在顶板自重及上覆岩层压力作用下，首先会产生瞬时弹性变形，此时等效矿柱的有效刚度为k′，式(3)变为式(12)。

D▽2▽2w+k′w=q

(12)

求解式(12)得顶板变形下沉位移w0为式(13)。

(13)

根据Reissner厚板弯矩公式求得顶板四个边的中点处弯矩最大，即在(a/2,0)和(a/2,b)处，Mx达到最大，见式(14)。

(14)

由最大弯矩公式可知，顶板长边边长a>b，|Mx|>|My|，顶板长边将先于短边发生破裂，采空区顶板长边最大应力为式(15)。

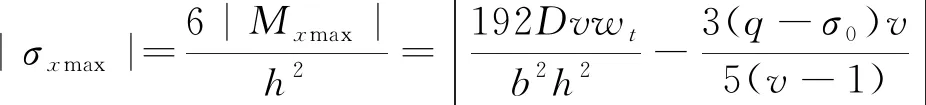
(15)

当|σxmax|≥[σT],即顶板长边最大应力大于顶板的极限抗拉强度时，顶板长边发生破裂，此时，采空区顶板并未发生整体失稳，而在长边边界处形成塑性铰，短边依旧为固支，顶板由四边固支状态变为固支-简支状态，由顶板长边最大应力和极限抗拉强度关系可求解顶板由四边固支变为固支-简支时的极限沉降位移。

2) 当采空区顶板由固支变为固支-简支状态后，此时顶板的边界条件为式(16)。

(16)

根据顶板的边界条件，取顶板挠度试函数为式(17)。

(17)

显然，f(x,y)满足顶板边界条件，将f(x,y)带入式(7)，可得

顶板在短边中点处弯矩达到最大，即在(0，b/2)和(a，b/2)处弯矩最大，值的计算见式(18)。

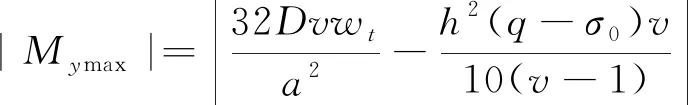
(18)

则顶板短边处最大应力为式(19)。

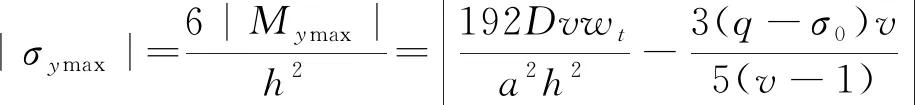
(19)

当|σymax|≥[σT],即顶板短边最大应力大于等于顶板岩体极限抗拉强度时，顶板短边发生破裂，此时顶板未发生整体性失稳，顶板短边出现塑性铰，顶板由固支-简支状态变为完全简支状态，可根据短边最大应力关系求解顶板长边破裂到短边破裂过程的极限沉降位移。

3) 当采空区顶板四边由固支变为简支后，边界塑性区开始向顶板内部延伸，当四边塑性区在顶板内部汇聚时，顶板出现失稳，此时的顶板边界条件为式(20)。

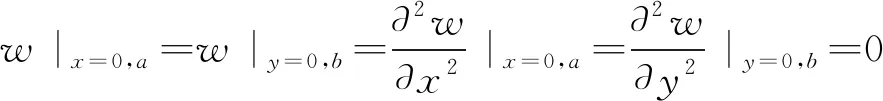
(20)

假设此时的顶板挠度试函数为式(21)。

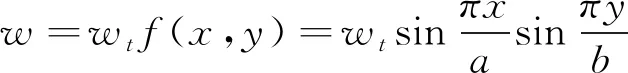
(21)

对于四边简支的采空区顶板，在顶板中心处，顶板应力最大，即在(a/2,b/2)处，达到最大，分别为式(22)和式(23)。

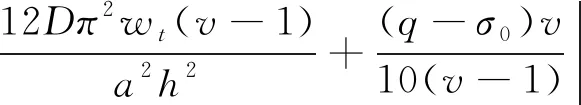
(22)

(23)

当顶板中心最大应力满足|σxmax|≥[σT]和|σymax|≥[σT]时，顶板中心发生失稳，可根据此时顶板中心最大应力关系求解顶板由简支状态到发生内部失稳破坏的极限沉降位移：沿x方向的位移wx、沿y方向的位移wy。

根据以上计算分析，采空区顶板发生破坏经历了四个主要阶段：固支阶段、固支-简支阶段、简支阶段、中心破坏阶段。 由上述公式可求解出各阶段顶板沉降位移，代入式(9)即可求出各阶段沉降时间。

3 案例分析

以贵州省某金矿为例，该矿采用全面法进行矿山开采，采场内留有支撑矿柱，空区上覆岩层厚度约为h1=150 m，上覆岩层平均容重为r1=24 kN/m3，顶板岩体为稳定性较差的软质岩，厚度h=48 m，容重约为r=23 kN/m3，近似将采空区看作矩形区域，顶板长度约为120 m，宽度约为115 m，弹性模量为11.2 GPa，泊松比为0.28，顶板岩石极限抗拉强度为[σT]=4.08 MPa，矿柱平均高度约为H=2.2 m，矿柱总横截面积占顶板总面积约为λ=34.4%,相关流变参数为E1=4.1 GPa，E2=261.21 MPa，η=26.25 GPa·d。计算过程如下所述。

1) 顶板上的均布荷载q=h1r1+hr=150×24+48×23=4.704 MPa；

2) 顶板的抗弯刚度D=Eh3/(12×(1-v2))=110×106MPa·m3；

3) 矿柱初始弹性变形阶段顶板下沉位移由式(13)计算得w0=0.382 cm；

4 结 论

1) 基于Reissner厚板理论建立了采空区矿柱-顶板系统力学模型，结合矿柱流变本构方程推导出顶板变形下沉位移关于流变时间的公式，该力学模型能够更好地反映顶板-矿柱体系的受力特征。

2) 根据各边界条件计算分析结果，随着矿柱流变变形，顶板在下沉过程中长边边界中点将最先发生破坏并向两侧扩展；之后短边中点将发生破坏，并逐渐发展至顶板四周破坏，破坏区开始向内部延伸，直至顶板发生整体失稳。

3) 顶板下沉量随矿柱流变时间增长而增加，计算所得顶板破坏时间可为采空区及时处理提供一定参考依据。