NA样本下随机设计情形线性模型的经验似然

付鸿涛卢维学，杨世娟

（1.上饶市广丰区公安局，江西 上饶 334000；2.黄山学院 数学与统计学院，安徽 黄山 245041）

NA样本下随机设计情形线性模型的经验似然

付鸿涛1，卢维学2，杨世娟2

（1.上饶市广丰区公安局，江西 上饶 334000；2.黄山学院 数学与统计学院，安徽 黄山 245041）

在NA样本下，利用大小分块方法和矩不等式首次构造并证明了随机设计情形下的线性模型的回归系数的经验似然比统计量的极限分布近似服从卡方分布，并进而构造其经验似然方法下的置信域，最后，模拟比较得出经验似然法下的置信域优于正态逼近法下的置信域。

线性模型；随机设计；分块经验似然；NA样本；置信域

0引　言

随着近期大数据及“互联网+”的大力推行，数据挖掘会日渐成为研究的焦点，如教育、医学、股市等领域的数据。上述数据都会出现的共同特点是相依和不完全等特性。诸如此类问题，研究者们极其希望在理论上能够更深入研究，以便对应用研究奠定基础。

NA的概念由Block et al.［1］和Joag-Dev and Proschan［2］第一次研究，之后国内外学者对其的研究涉及了多元统计分析、渗透理论等诸多方面［3-7］。

Owen［8］首次系统地提出解决非参数估计推断的经验似然方法，此法构造置信区间具有域保持性、变换不变性等诸多优点，对此该方法被应用到各种统计模型的研究中，且涉及到诸多领域［9，10］。

1　预备知识

考虑如下线性模型：

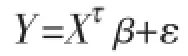
其中，Y是一维响应变量，X∈Rd是随机向量，β∈Rd是回归系数组成的向量，ε∈R是随机残差且满足E（ε|X）=0。假设X1，X2，…，Xn为X的观测值，Y1，Y2，…，Yn为Y的样本观测值，｛X1，Y1，X2，Y2，…Xn，Yn｝为NA序列。

2　主要结果

为了构造β的置信域，对其定义的经验似然的得分函数的和进行分块，即对n的和分成如下大小块，记：

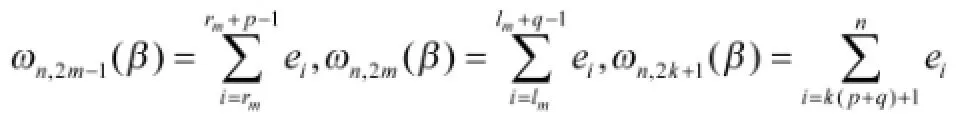
其中rm=（m-1）（p+q）+1，lm=（m-1）（p+q）+p+1，m= 1，2，…，k，k=［n/（p+q）］，［t］代表t的整数部分，且p=p（n）和q=q（n）满足p+q≤n。

分块经验似然比统计量如下：

通过上式得出（-2log）分块似然比统计量：

其中λ（β）∈Rd由下式确定

为了证明方便，给出记号用Xij记Xi的第j个分量，1≤i≤n，1≤j≤d用||x||表示向量x的L2范数，矩阵A的特征值的最小和最大值分别记为λmin（A）和λmax（A）。为了构造得到l（β）的极限分布，假设条件如下：

（A1）（i）｛X11，X12，…，X1d，Y1，X21，X22，…，X2d，Y2，…，Xn1，Xn2，…Xn d，Yn｝，为NA随机变量序列，且｛Xi，1≤i≤n｝，｛Yi，1≤i≤n｝均为平稳序列.

（iii）X和Y均有界。

（A2）如上面所描述的p，q和k，记h＞0为窗宽，并满足

若zα使得成立。由定理1知，β渐近水1-α的经验似然置信域为

3　模拟结果

由（3）确定的β的经验似然置信域记为ELCI，β的正态逼近的置信域记为NACI，为了比较ELCI和NACI的置信域比率 （CP）和置信区间的平均长度（AL）。考虑如下模型｛X1，Y1，…，Xn，Yn｝服从多元正态分布（N：p1，p2，…，p2n）（4）

分别模拟样本容量为n=100，150，200和250的情形，且重复1000次，在此选择参数p=［n1/6］，q= ［n1/8］显著水平α=0.05，表1给出模拟结果：CP随着样本容量的增大而越接近显著水平0.95，AL随着样本量的增加而减小，且ELCI的覆盖精度比NACI的覆盖精度高。

表1　ELCI与NACI置信域比率和置信区间的平均长度

4　引理及定理1的证明

引理1：假设｛ηj：1≤j≤n｝是NA随机变量序列并满足是一个实数列，则存在常数C（与所给的s有关）使得

且

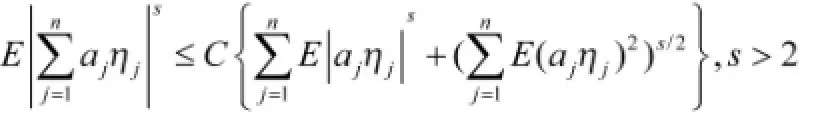
证明：见Shao［11］。

引理2：假设A1A2为两个无公共元素的整数子集，且｛ηj，j∈A1∪A2｝为NA随机变量序列。函数和的偏导数都存在且有界，用表示g的偏导数的上确界，则有

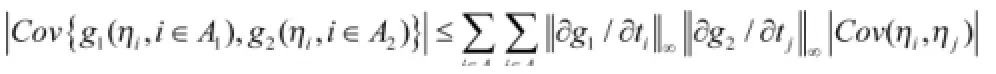
其中ηj表示Aj中元素的个数 j=1，2。

证明：参考 Bulinski［12］引理 1与 Cai and Roussas［13］引理3.5的论证过程。

引理3：设条件（A1）与（A2）成立，且由常数构成的向量l∈Rd满足||l||=1，则当n→∞时有

证明：首先证明（5），注意到

为了证明（6），只需证明：对给定的l∈Rd且||l||= 1，有

故为证（7），只需证明

首先证明

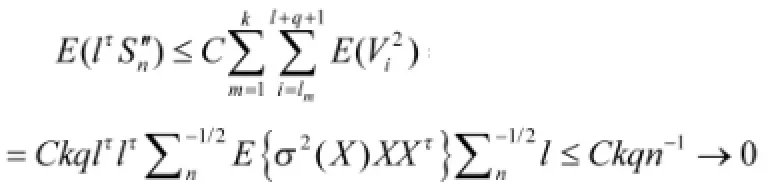
类似可证

利用（11）和（12），可以得到

此外，由平稳性和Roussas［14］的引理3.2有

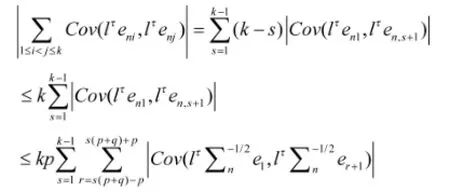
根据引理2和（5）式，可得

由引理2和序列的平稳性，结合Roussas［14］中的定理2.1证明过程，可得

假设｛ηnm，1≤m≤k｝为独立随机变量序列，ηnm和有相同的分布。故为证（8），只需证明

由引理1和（5）知

由（11）和（12）知（9）和（10）成立，故引理3证毕。

引理4：在定理1的条件下，当n→∞时，有

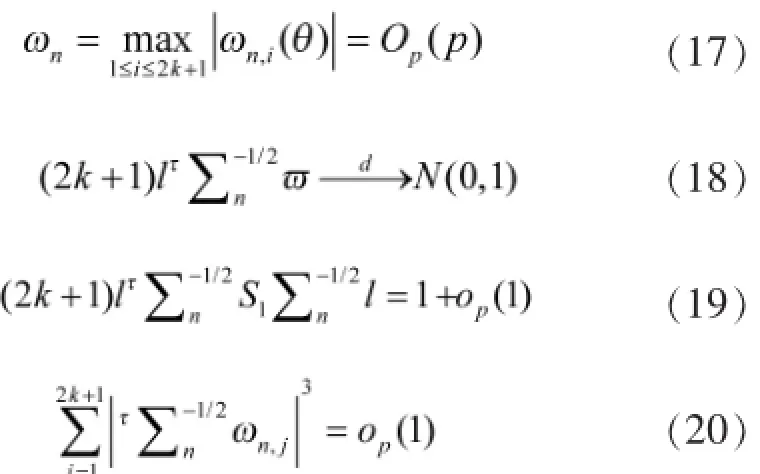
由引理3的证明过程可知

故为证（19），只需证明

令

由于f1（x），f2（x）都是单调函数，故都是NA随机变量，又有

由引理1，类似于（16）的证明可得

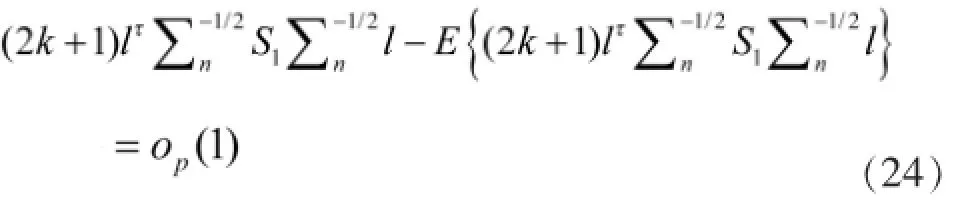
由（21）和（24）可得

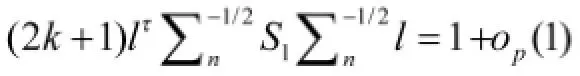
下面证明（20），

由引理1知

同理有

由（25），（26），（27）可得：Tnj=op（1），1≤j≤3从而（20）式得证。

定理1的证明：

知

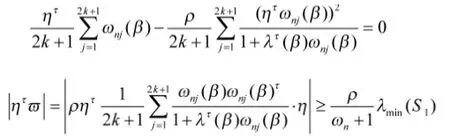
进而

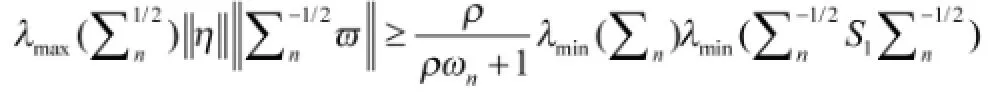
结合引理4得

从而

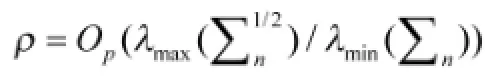
结合引理3知p=Op（n-1/2）再次利用（28）得

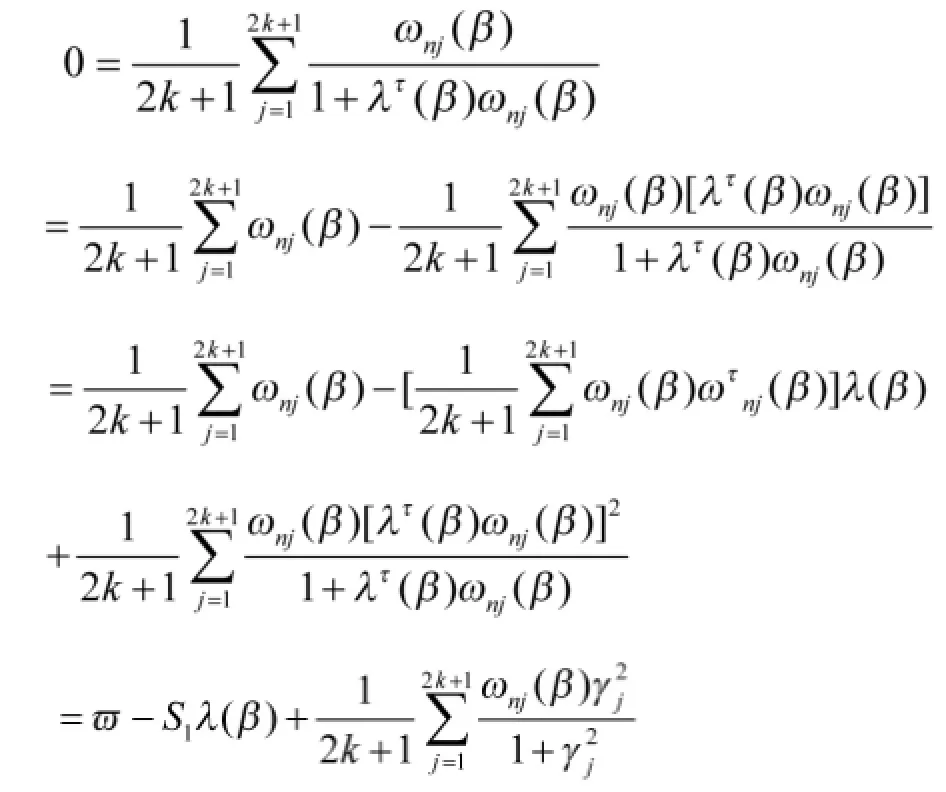
故

其中

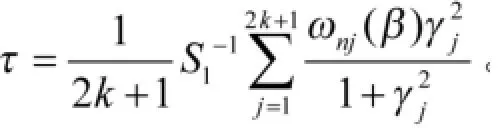
由引理3和引理4知

其中ηj满足

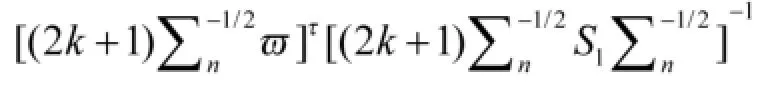
进一步有

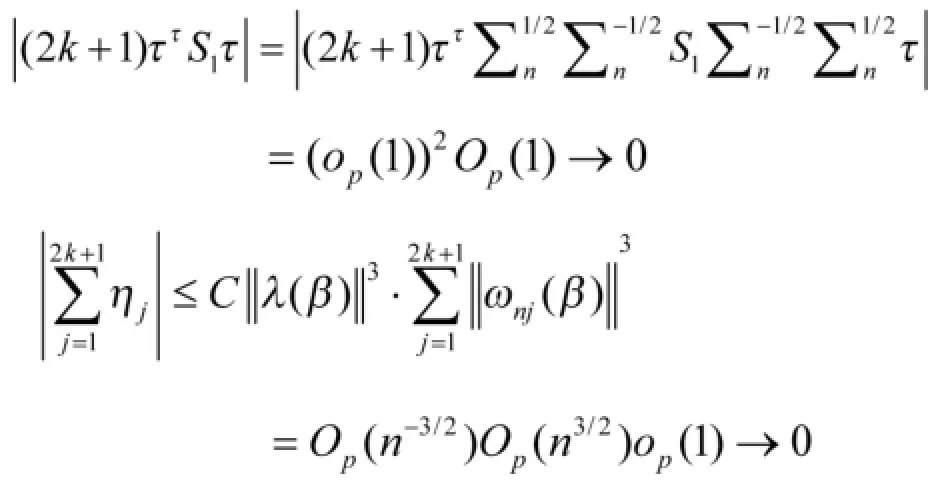
从而定理1得证。

［1］Block，H.W.and Savits，T.H.Sharked，M.Some conceots of negative dependence［J］.The Annals of Probability，1982，10：765-772.

［2］Joag-Dev，K.and Proschan，F.Negative association of random variables with applications［J］.The Annals of Statistics，1983，11：286-295.

［3］Lei，Q.and Qin，Y.Confidence intervals for nonparametric regressionfunctionswithmissingdata：multipledesign case［J］，Journal of Systems Science and Complexity，2011，24：1204-1217.

［4］Qin，Y.and Li，Y.Empirical likelihood for linear models under negatively associated errors［J］.Journal of Multivariate Analysis，2011，102：153-163.

［5］Su，L.Zhao，C.Wang，Y.B.Moment inqualities and week convergence for negatively associated sequences［J］，Science China，1997，40：172-182.

［6］Thomas，D.R.and Grunkemeier，G.L.Confidence interval estimation of survival probabilities for censored data［J］. Journal of the American Statistical Association，1975，70：865-871.

［7］苏淳.NA序列的一个Hsu-Robbins型定理 ［J］.科学通报. 1996，41：106-110.

［8］Owen，A.B.Empirical likelihood ratio confidence intervals for a single functional［J］.Biometrika，1988，75：237-249.

［9］Owen，A.B.Empirical likelihood ratio confidence regions ［J］.The Annals of Statistics，1990，18：90-120.

［10］卢维学，杨世娟，李英华.混合样本下分布函数在有限点的联合渐近分布［J］.广西师范大学学报.2014，32：67-74.

［11］Shao，Q.M.A comparison theorem on moment inequalities betweennegativelyassociatedandindependentrandom variables［J］.Journal of Theoretical Probability，2000，13：343-356.

［12］Bulinski，A.V.and Keane，M.S.Invariance principle for associated random fields［J］.Journal of Mathematical Sciences，1996，81：2905-2911.

［13］Cai，Z.W.and Roussas，G.G.Berry-esseen bounds for smooth estimator of a distribution function under association［J］.Journal of Nonparametric Statiatics，1999，11：79-106.

［14］Roussas，G.G.Asymptotic normality of the kernel estimate of a probability density function under association［J］. Statistics and Probability Letters，2000，50：1-12.

责任编辑：胡德明

Empirical Likelihood for Linear Models with Random Designs under Negatively Associated Samples

Fu Hongtao1，Lu Weixue2，Yang Shijuan2
（1.Public Security Bureau of Guangfeng District，Shangrao 334000，China；2.School of Mathematics and Statistics，Huangshan University，Huangshan 245041，China）

Under the samples of negative association，empirical likelihood of regression coefficient in linear models with random designs is first constructed and proved by blocking method and moment inequalities.And then the confidence regions based on empirical likelihood are constructed.Simulation studies show that confidence regions based on empirical likelihood is better than those based on normalapproximation.

linear models；random design；block empirical likelihood；samples of negative association；confidence region

O212.2

A

1672-447X（2016）03-0001-006

2016-03-20

黄山学院自然科学研究项目（2015xkj004；2015xkj005），安徽省教育厅自然科学研究项目（KJHS2016B04）。

付鸿涛（1987-），江西上饶人，硕士，上饶市广丰区公安局，研究方向为应用统计；卢维学（1989-），黑龙江依安人，硕士，黄山学院数学与统计学院助教，研究方向为数理统计。