递推数列的通项公式求法

邱家荣（云南省呈贡区第一中学）

递推数列的通项公式求法

邱家荣
（云南省呈贡区第一中学）

以各种类型的递推数列为模型，类比、化归到等差数列、等比数列，然后求出递推数列的通项公式，以期提高学生适应高考的能力，提升学生解题的思维品质。

递推数列；等差数列；等比数列

在最近几年全国各地的高考试题中，绝大多数数列考题都考查了递推数列通项公式的求解。递推数列通项公式的求解，主要运用转化思想把问题化归为两个基本数列——等差数列、等比数列的问题来求解。把数学运用于实践，有意识地从这两个方面培养学生的学习能力和解题能力。

1.型如an+1=an+f（n）的通项求法：将已知化为an+1-an=f（n）用累加求解。

注：当f（n）为常数d时，型如一就为等差数列。

例1.已知数列｛an｝满足a1=2，an+1=an+2n+3（n∈N*），求an．

分析：由递推关系an+1=an+2n+3⇒an+1-an=2n+3有：

故：an=n2+2n-1（n∈N*）

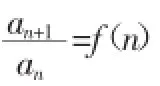
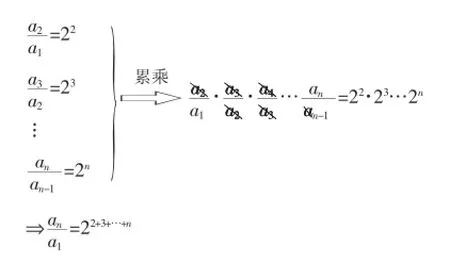
例2.已知数列｛an｝满足a1=3且an+1=2n+1an，求an

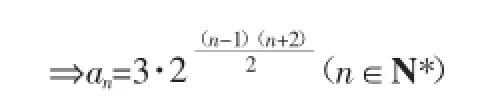
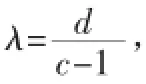
例3.已知数列｛an｝满足a1=1，an+1=2an+1（n∈N*），求数列｛an｝的通项公式；

分析：转化成两种基本数列利用两法求解。

解：∵an+1=2an+1（n∈N*），

∴an+1+1=2（an+1），

∴｛an+1｝是以a1+1=2为首项，2为公比的等比数列，

∴an+1=2n

即an=2n-1（n∈N*）

（1）派生一，型如：an+1=can+An+B（其中A，B，c为常数）的通项求法：将已知化为an+1+λ1（n+1）+λ2=c（an+λ1n+λ2）可得｛an+λ1n+λ2｝是等比数列。

例4.已知a1=2且an+1=4an+6n-5求｛an｝的通项公式。

解：因an+1=4an+6n-5可化为an+1+2（n+1）-1=4（an+2n-1）

则｛an+2n-1｝是首项为a1+2-1=3，公比为4的等比数列，

所以an+2n-1=3·4n-1

即an=3·4n-1-2n+1

（2）派生二，型如：an+1=man+An2+Bn+C（其中m、A、B、C为常数）的通项求法：将已知化为an+1+λ1（n+1）2+λ2（n+1）+λ3=m（an+ λ1n2+λ2n+λ3）可得｛an+λ1n2+λ2n+λ3｝是等比数列。

例5.已知a1=2且an+1=3an+2n2-6n+7求｛an｝的通项公式。

解：因an+1=3an+2n2-6n+7可化为：

an+1+（n+1）2-2（n+1）+3=3（an+n2-2n+3）

得｛an+n2-2n+3｝是首项为a1+12-2+3=4，公比为3的等比数列。

则an+n2-2n+3=4·3n-1

即an=4·3n-1-n2+2n-3

（3）派生三，型如：an+1=can+dn（其中c、d为不相等的常数）的通项求法：将已知化为an+1+λdn+1=c（an+λdn）可得｛an+λdn｝是等比数列。

例6.已知数列｛an｝的首项为a1=1且an+1=2an+3n，求通项an。

解：因an+1=2an+3n可化为an+1-3n+1=2（an-3n）

得｛an-3n｝是首项为a1-3=-2公比为2的等比数列

则an-3n=-2·2n-1。

即an=3n-2n

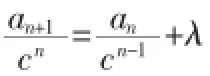
例7.已知，数列｛an｝的首项a1=2且an+1=2an+3·2n，求通项an。

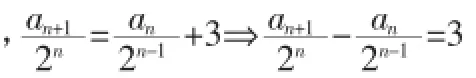
即an=（3n-1）2n-1

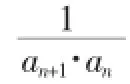
6.型如：an+1=c（其中c＞0，an＞0）的通项求法：将已知两边取对数转化为lgan+1=2lgan+lgc用第3种形式求解。

［练习］

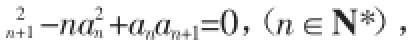
3．已知数列｛an｝中，a1=1，a2=3且an+2=3an+1-2an，则an=_______；

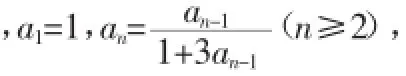
6.设数列｛an｝首项为1，an+1-an=2an+1an，求数列｛an｝的通项公式。

7.设数列｛a｝n首项为2，an+1=100，求数列｛an｝的通项公式。

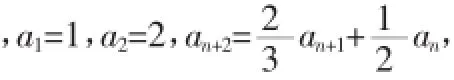
［1］黄爱民.十类递推数列的通项公式的求法［J］.高中生，2006（10）：12-13.

［2］吴怀芳.求数列通项的几种常见类型［J］.试题与研究，2005（9）.

［3］陈云烽.递推数列通项的求解［J］.中学数学教学参考，2007（6）.

·编辑李琴芳