一种信息检索中语义相似度的计算方法

时慧琨

（淮南师范学院 计算机学院，安徽 淮南 232038）

一种信息检索中语义相似度的计算方法

时慧琨

（淮南师范学院 计算机学院，安徽 淮南 232038）

语义相似度计算在自然语言处理及信息检索领域有着广泛的应用。在总结已有相似度计算方法基础上，考虑信息检索中语义扩展的不对称现象，结合不对称语义计算模型提出了一种信息检索中非对称语义相似度计算方法，先计算本体中每对上下位概念之间的相似度，并基于距离的相似度计算模型计算出任意概念之间的相似度。实验表明可以用于信息检索中语义扩展，为概念间相似度的衡量提供更准确的结果。

信息检索；语义扩展；语义相似度；本体

语义相似度计算在信息检索、信息推荐和过滤、机器翻译、本体学习、文本分类和聚类等领域都有着极为广泛的应用，在信息检索领域，语义相似度计算可以用于对信息查询进行语义扩展［1］。在这个过程中，如何计算扩展词和用户输入词的相似程度是关键所在。计算依据的信息来源以及如何计算相似度是不同语义扩展技术的主要区别。常见语义扩展依赖的信息来源主要有词典（如Word-Net、知网）、语料库、网络百科全书（如Wikipedia、百度百科）、本体等形式。其中，本体作为一种“共享概念的明确的形式化规范说明”，能够明确、形式化地表达领域内的各种概念及相互关系，提供该领域知识的共同理解，在语言研究及应用方面发挥着重要作用，基于本体的语义相似度计算方法也已成为语义信息检索技术的重要研究内容［2］。

本文针对传统语义相似度计算方法的优缺点，结合信息检索对相似度计算的特定要求，提出了一种检索应用下的不对称语义相似度计算方法。在本体中综合方向、信息内容及本体结构等特性计算上下位概念间的距离，并在基于距离的相似度计算模型基础上求解本体中任意概念之间的距离及相似度。计算的结果全面考虑了相似度的影响因素，计算结果更加合理，也更适应信息检索应用的需求。

1　本体及基于本体的语义相似度计算

从结构上看，本体是一个有明显层次特征的图状结构，图中结点表示本体中的概念或者实例，结点之间的边表示关系，常见的关系包括同义、继承、部分整体、概念实例关系等。两个概念的相似度通常在［0，1］之间。在计算本体中概念间相似度时，主要基于概念本身的性质及概念之间的关系，这些性质或关系通常被表示成因子，按照因子的来源可以将其分成基于结点的因子和基于边的因子两大类。

基于结点的因子根据概念自身的特性计算得出，常见的因子有：

（1）属性因子：概念的属性描述了概念的特征，这些属性即构成了属性因子。如果两个概念的很多属性相同，则这两个概念也比较相似。

（2）语义深度因子：语义深度因子与概念在本体图中所在的层次有关。本体中的下层概念是对上层概念的细化，因此，概念层次越高，对应语义范畴越大，同层结点之间的距离也越大，相似度就越小。越往下层，概念之间距离就越小，相似度就越大。

（3）语义重合度因子：该因子和两个概念结点的共同祖先有关。认为两个概念的共同祖先代表了两个概念中相同的内容，共同祖先的信息量越大，则两个概念就越相似。信息量常按照信息论的观点，通过概念出现的频率来进行计算。

（4）结点密度因子。该因子和结点的度有关，反映了结点所在局部的性质。结点的度越大，表明结点在此处的分化越多，子结点之间的距离就越小，节点之间越相似。

本体中的边代表了概念之间的关系，反映了概念之间的联系，概念间的相似度也可以通过概念间关系计算得出。常见基于边的因子有：

（1）类型因子。本体中常见的关系类型包括同义、继承、整体部分及概念实例关系等，不同关系对应的相似程度是不同的，同义概念可以认为其相似度等于1，但是其他关系的相似度一般小于1。对类型因子的确定常采用专家指定的方式。

（2）距离因子。将本体看成一个连通图，通过计算概念间的距离来衡量相似度，距离越长，相似度越小。

（3）深度因子。该因子考虑了边在本体层次图中所在的层次。边的层次越低，边关联的两个概念间距离越近，就越相似。

（4）密度因子。密度因子考虑了子概念对父概念的细化程度，结点的度越大，则细化程度越大，密度因子值就越大。

（5）有向边的方向。通常认为概念间相似度具有对称性，即对于概念A和B，sim（A，B）=sim（B，A）。但有些研究注意到相似度之间的方向性，认为由于子概念具有父概念的全部特征，但父概念不一定具有子概念的特征，因此，父结点相对于子结点的相似度小于子结点相对于父结点的相似度。在此基础上出现了不对称的语义相似度计算方法［3］。

由于本体中的边依附于顶点，因此，基于结点的因子和基于边定义的因子间具有一定的相关性，例如：结点的语义深度因子和边的深度因子之间、结点的密度因子和边的密度因子之间都是相关的。在计算概念之间语义相似度时，需要合理选择因子，一方面可以降低计算的复杂度，另一方面也降低了在对各种因子综合时加权因子确定的难度。

在计算语义相似度因子的基础上，计算概念之间的相似度。按照选取的因子及计算方法的不同，常见的相似度计算模型有三种：

（1）基于距离的计算模型［4］。该模型认为两个概念的相似性和两者间距离有关，距离越近则越相似。最简单的概念间距离就是本体图中概念间最短路径的长度。这种计算认为本体中每条边对应的距离或权重相等，更复杂的方法是基于其它因子设置每条边的权重，然后再计算距离及相似度。

（2）基于内容的计算模型［5］。该模型在计算每个概念信息量的基础上，基于语义重合度因子计算概念间的相似度。

（3）基于属性的计算模型［6］。该模型基于概念的属性因子，通过概念的相同属性来计算概念间的相似度。

在这些计算模型中，基于距离的计算模型主要利用了基于边定义的因子，基于内容和基于属性的模型则利用了基于结点定义的因子。由于因子只是反映了概念或关系在某个方面的特性，因此计算出的相似度往往并不能全面衡量概念间相似度，改进的途径就是在计算相似度时综合考虑各方面的因素，出现了各种加权的方法［7］。但目前选择哪些因子、因子权重的设置并没有统一的标准，计算结果的主观性较大。这一方面是因为相似性衡量本身就带有较大的主观性，相似度计算也缺乏客观公认的评价标准，另一方面也说明相似度计算仍然需要进一步的研究。

2　面向信息检索的非对称语义相似度计算方法

语义扩展时需要考虑概念之间的相似性，将语义扩展技术应用到信息检索时，相似性主要表现为扩展概念满足用户查询需求的能力。从这一点上来说，同义关系的词之间能够100%满足用户需求，其相似度为1，其它关系对应的相似度在［0，1］之间。

在本体常见关系中，同义关系是对称关系，但其它的如继承关系、整体部分关系、概念实例关系都不是对称的，关系的不对称性从根本上导致了相似度衡量时的不对称性。在对非同义关系的概念的相似度进行计算时，得到的相似度也不应该相同。以本体中最常见的继承关系为例，假设概念A 和B是一对上下位概念，通常B是对概念A进行细化的结果，即按照某种属性对A进行了划分得到了B及其它下位概念。因此在检索中，如果用A去扩展B，则由于A的范畴更大，查询结果中会包含用户不需要的信息，但是用B去扩展A时，由于B是下位概念，是A的一种，因此，返回结果仍然属于A的概念范畴。从这一点上来说，用B扩展A的相似度要大于用A去扩展B的相似度。定义sim（x，y）表示用x去扩展y时需要考虑的相似度，若A是B的上位概念，则sim（A，B）＜sim（B，A）。例如在数据结构本体中，对概念对（数据结构，树），用“数据结构”去扩展“树”的相似度要小于用“树”去扩展“数据结构”时的相似度，即sim（数据结构，树）＜sim（树，数据结构）。

考虑如上概念相似度不对称的情况，在基于距离的相似度计算模型［8］基础上，提出相似度计算方法如下：

（1）依据本体结构，计算本体中每对上下位概念之间的距离。计算过程如下：

1）基于概念出现的频率，计算每个概念的信息量。由于上位概念的语义范畴包含了其所有的下位概念，因此其出现的频率应包含其所有下位概念的出现频率，对概念，定义其信息量，其中

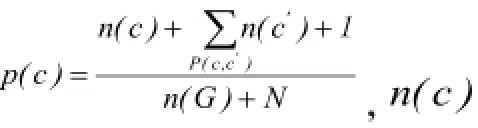
2）计算概念间的内容因子。两个概念共享的信息量越多，则两个概念越相似。对于上下位概念来说，上位概念的信息量是两者共有的信息量，下位概念的信息量是全部的信息量。在相似度计算时，使用扩展概念与原有概念信息量的比值表示扩展概念对原概念的语义覆盖能力，因此定义内容因子。定义上下位概念分别为和，当使用概念去扩展概念时，，当使用去扩展时，由于下位概念中包含了上位概念的全部信息，因此。

3）内容因子主要考虑了概念自身的特性，而概念之间相似度还和概念在本体中的位置有关。为此，引入了边的深度因子和密度因子。分别表示本体中垂直和水平方向上对概念间相似度的影响因素。对概念和概念来说，定义：深度因子

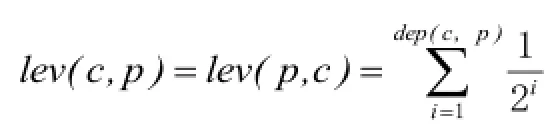
4）综合内容因子、深度因子和密度因子，计算本体中每一条有向边的权重。概念替换时的权重，概念替换时的权重，其中为各因子的权重系数，

（2）计算本体中任意两个概念之间的距离。

将本体看成一个概念层次网络，根据基于距离的相似度计算模型，在本体中寻找从起点到终点的最短路径，并将最短路径上各条有向边的距离因子加起来，作为到的距离。

（3）计算概念间的语义相似度定义

3　实验验证及结果

实验中定义的本体如图1所示，

图1　数据结构本体

按照以上列出的计算方法，取a=0.7，b=0.1，c=0.2，α=0.5，θ=10。选取本体中的典型概念计算其相似度，结果如下：

（1）sim（单向链表，无向图）=0.08，sim（单向链表，图）=0.11。由于前两者的路径长度要大于后两者的路径长度，从计算结果可以看出，路径越短，计算得到的相似度值越大，两个概念间越相似。

（2）sim（树，线性结构）=0.27，sim（队列，栈）= 0.62。考虑概念所在的深度，深度越低，兄弟结点间相似度越大。但这个相似度与深度的对应关系越往下层越不明显，甚至有可能小于上层结点的相似度。因为两个概念间的相似度不仅受深度影响，还有概念内容，密度等因素制约。

（3）sim（数据结构，线性结构）=0.37，sim（线性结构，数据结构）=0.88。这一对计算结果反映了相似度之间的不对称性，由于数据结构相对于线性结构来说概念的范畴进行了扩大，因此得到的相似度要小于反方向上的相似度。

（4）sim（数据结构，线性表）=0.23，sim（线性表，数据结构）=0.67。这一对计算结果也反映了相似度之间的不对称性。把它和（3）的计算结果对应起来可以看出，由于数据结构和线性表间的深度差异要大于和线性结构之间的深度差异，因此无论是哪个方向上的相似度均比（3）的计算结果要小。这样的计算结果更符合人们的主观感受。

4　结论

本文在总结基于本体的语义相似度计算因子及计算模型的基础上，分析了信息检索过程中语义扩展时扩展词与查询词之间的关系，基于非对称语义模型和基于距离的相似度计算模型提出了一种非对称的语义相似度计算方法。该方法综合考虑了概念的内容及本体的结构，计算结果能够更好的符合人们的主观认识。计算方法中主要考虑了概念间的继承关系，综合考虑各种关系基础上进行计算是下一步继续研究的内容。

［1］黄名选，严小卫，张师超.查询扩展技术进展与展望［J］.计算机应用与软件，2007，24（11）：1-4.

［2］刘宏哲，须德.基于本体的语义相似度和相关度计算研究综述［J］.计算机科学，2012，39（2）：8-13.

［3］张兰芳.一种基于本体的自然语言语义相似度算法［J］.桂林理工大学学报，2012，32（2）：253-258．

［4］Leacock C，Chodorow M.Combining Local Context and Word-Net Similarity for Word Sense Identification［M］//WordNet：An Electronic Lexical Database.Cambridge，MA：MIT Press，1998：265-283.

［5］Lin D.An Information Theoretic Definition of Similarity［C］//Proceedings of the International Conference on Machine Learning，1998：296-304.

［6］Tervsky.Feature of Similarity［J］.Psychological Review，1977，84 （4）：327-352.

［7］曹叡，吴玲达.一种改进的领域本体语义相似度计算方法［J］.微电子学与计算机，2014，31（8）：109-114．

［8］黄果，周竹荣.基于领域本体的概念语义相似度计算研究［J］.计算机工程与设计，2007，28（10）：2460-2463.

［责任编辑：桂传友］

Semantic Similarity Computation of an Information Retrieval

Shi Huikun
（College of Computer Science，Huainan Normal University，Huainan Anhui 232038）

Semantic similarity computation is widely used in natural language processing and information retriev⁃al.Asymmetric semantic similarity computation of information retrieval is put forward based on the existed similar⁃ity computation and asymmetry of semantic extension in information retrieval and asymmetric semantic computing models，which firstly computes the similarity between ontology and the concept of superordination and subordina⁃tion，and then computes the similarity of arbitrary concepts based on distance similarity computing models.The experiment shows the computation can be applied to semantic extension of information retrieval and provides pre⁃cise results for evaluation of concept similarity.

Information Retrieval；Semantic Extension；Semantic Similarity；Ontology

TP391

A

1674-1102（2016）03-0026-04

10.13420/j.cnki.jczu.2016.03.006

2015-12-05

安徽省高校省级自然科学研究项目（KJ2012Z375）。

时慧琨（1975-），男，安徽淮南人，淮南师范学院计算机学院讲师，硕士，研究方向为信息处理，人工智能。