含割边的连通图最小距离无符号拉普拉斯谱半径

查淑萍，李路遥，高　芳

（池州学院 数学与计算机学院，安徽 池州 247000）

含割边的连通图最小距离无符号拉普拉斯谱半径

查淑萍，李路遥，高芳

（池州学院 数学与计算机学院，安徽 池州 247000）

在所有含割边的n阶连通图中，利用特征值与特征向量的关系，刻画了具有最小距离无符号拉普拉斯谱半径的图的结构，在此基础上，给出了含割边的n阶连通图的距离无符号拉普拉斯谱半径的一个下界。

图；割边；距离无符号拉普拉斯矩阵；谱半径

1　引言

本文中，我们只考虑简单的连通图G=（V（G），E（G），这里V（G）表示图G的顶点集，E（G）表示图G的边集，其中||V（G）称为图G的阶数。图G的距离矩阵，记作D（G），定义为D（G）=（duv）u，v∈V（G），其中duv表示顶点u和v之间的距离（即G中连接u和v的最短路的长度）。其广泛应用涉及很多领域，如通讯网络的设计［1］，图的嵌入理论［2-4］以及分子稳定性［5-6］等。顶点v的距离度，记作Tr（v），定义为v与G中所有顶点的距离之和，即Tr（v）=∑u∈V（G）duv，记G中顶点的最大距离度为Trmax（G）。

2013年，M.Aouchiche和P.Hanse［7］在距离矩阵的基础上，定义了连通图G的距离无符号拉普拉斯矩阵为DQ（G）=Diag（Tr）+D（G），这里Diag（Tr）表示以G的各顶点的距离度为对角元的对角矩阵。显然，DQ（G）是实对称的正矩阵，故由对称矩阵与非负矩阵理论［8］可知，其特征值全为实数，并且最大特征值恰为DQ（G）的谱半径ρ（G）。另外，最大特征值的代数重数为1，其对应的的特征向量中各分量符号一致，为方便起见，本文中将属于ρ（G）的分量全正的单位特征向量称为Perron向量。基于极图理论研究的重要性，近年来，关于刻画距离无符号拉普拉斯谱半径极图的研究也逐渐成为新的研究热点。如：R.Xing和B.Zhou等［9-10］分别刻画了n阶树、单圈图、双圈图、二部图、给定悬挂点的图类以及给定连通度的图类中距离无符号拉普拉斯谱半径最小图的结构；G.D.Yu等［11］研究了具有n-3个悬挂点的n阶树的距离无符号拉普拉斯谱半径的极小值，并刻画了一类n阶具有n-3个悬挂点的树的距离无符号拉普拉斯谱半径的极小值和极大值；本文的第一作者［12-13］参与刻画了给定染色数和含割点的图类中距离无符号拉普拉斯谱半径极小图的结构；K.C.Das［14］等获得了距离无符号拉普拉斯谱半径关于独立数的一个下界，并刻画了相应的极图；Wrong dein等［15］证明了M.Aouchiche和P.Hanse在文［7］中提出的关于距离拉普拉斯矩阵的最大和第二大特征值以及距离无符号拉普拉斯矩阵的第二大特征值的四个猜想。

受上述成果的启发，本文研究了在含割边的连通图类中，距离无符号拉普拉斯谱半径极小图的结构，并在此基础上，获得了含割边的n阶连通图的距离无符号拉普拉斯谱半径的一个下界。

2　主要结果

设G为n阶连通图，V（G）=｛v1，v2，…，vn｝，对n维列向量 x=（x1，x2，…，xn）∈Rn，若建立映射 φ：V（G）→Rn，使得对任意的 i∈｛1，2，…，n｝，有xi=φ（vi），则x可视为定义在V（G）上的一个函数。不难发现，

若x是DQ（G）的对应于特征值λ的一个特征向量，则由特征值与特征向量的关系可知，x≠0且

对任意vi∈V（G）都成立，反之亦真。另外，由Rayleigh商理论［8］可知，对任意单位向量x∈Rn，

等式当且仅当x是DQ（G）的Perron向量时成立。

对于一个非负不可约矩阵而言，任一元素值的增大都将导致该矩阵谱半径的变大，基于这一理论，我们易得下述引理。

引理 2.1［12］设G是一个连通的简单图，且u，v∈V（G），则

（1）若uv∉E（G），则ρ（G）＞ρ（G+uv）；

（2）若 uv∈E（G）且 uv不是 G的割边，则ρ（G）＜ρ（G-uv）。

图G的距离无符号拉普拉斯谱半径与图G的顶点的最大距离度之间有以下不等式关系。引理

2.2［10］设G是一个连通图，则Trmax（G）＜ρ（G）≤2Trmax（G）。

设v∈V（G），记v在G中的邻域为N（v），则有，

引理2.3［12］设G是包含顶点u，v的连通图，则

（1）若N（u）｛v｝=N（v）｛u｝，则Tr（u）=Tr（v）；

（2）若N（u）｛v｝⊂N（v）｛u｝，则Tr（u）＞Tr（v）。

由引理2.3，我们可以得到下述引理。

引理2.4［12］设G是包含顶点u，v的连通图，x是DQ（G）的一个Perron向量。

（1）若N（u）｛v｝=N（v）｛u｝，则xu=xv；

（2）若N（u）｛v｝⊂N（v）｛u｝，则xu＞xv。

设G和H是分别含顶点u和v的两个不相交的连通图，在G的顶点u和H的顶点v之间添加一条边，形成的图，在本文中称为G与H的（uv）连图，记作G（u）↔H（v）。为方便起见，将完全图Kp与Kq的连图记作G（p，q）。

定理2.5设G是含割边的n阶连通图，则ρ（G）≥ρ（G（1，n-1）），等号当且仅当G=G（1，n-1）时成立。

证明 在所有含割边的n阶连通图类中，设G的距离无符号拉普拉斯谱半径最小，下面刻画G的结构。

首先G一定只含一条割边，设为uv。否则，若G含有两条割边e1和e2，则可以适当添加一些边，使得e2不再是割边，所得的图记为G′，由引理2.1，ρ（G′）＜ρ（G），矛盾！

其次，同样由引理2.1，G可视为两个完全图Kp与Kq的连图G（p，q），其中p+q=n，u∈V（Kp），v∈V（Kq）。不妨设 p≤q，则一定有 p≥1 且p≠2。首先我们假设p≥3，记G（p，q）的距离无符号拉普拉斯谱半径为ρ，对应的Perron向量为x。由于对任意的w1，w2∈V（Kp-u），N（w1）｛w2｝=N（w2）｛w1｝，故由引理2.4知，x的对应于Kp-u中所有顶点的分量一定相等，记为x1；同样的道理，对应于Kq-v中所有顶点的分量也一定相等，记为x2；记u所对应的分量为xu，v所对应的分量为xv。则由（2）得：

即，

于是ρ一定是方程 fp，q（λ）=0的最大根，其中

考虑多项式 fp，q（λ）与 fp-1，q+1（λ）的差，经过一些简单的计算，可得：

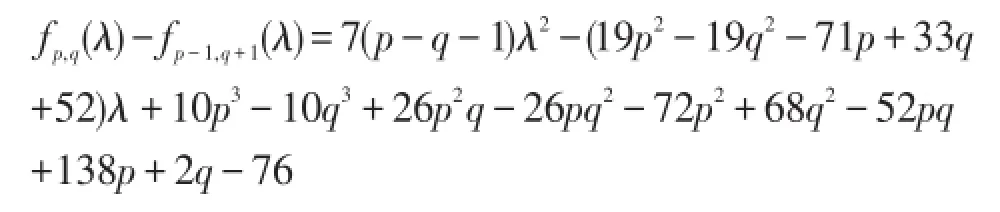
记G（p-1，q+1）的距离无符号拉普拉斯谱半径为ρ′，则由引理2.2得，ρ′≤2p+6q，故

注意到 fp-1，q+1（ρ′）=0，于是得 fp，q（ρ′）＜0。根据ρ为多项式 fp，q（λ）的最大根以及知，ρ′＜ρ。综合以上分析知，p=1，从而q=n-1。于是结论成立。

证明 由定理2.4，只需计算G（1，n-1）的距离无符拉普拉斯谱半径。根据G（1，n-1）的结构，类似于前面的记号，用u表示悬挂点，其邻点表示为v。记G（1，n-1）的距离无符号拉普拉斯谱半径为ρ，对应的Perron向量为x，则x的对应于顶点u的分量为xu，对应于顶点v的分量为xv，由定理2.4知，x的对应于其余顶点的分量都相等，记为x0，则由（2）得：

即，

于是ρ一定是方程f（λ）=0的最大根，其中

利用定理2.6，可以进一步得出含割边连通图的距离无符号拉普拉斯谱半径的一个下界。

推论2.7对任一含割边的连通图G，有ρ（G）≥2，其中等号当且仅当G=G（1，1）时成立。

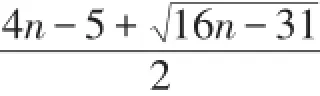
［1］R.L.Graham H.O.Pollak.On the addressing problem for loop switching［J］.Bell Sys.Tech.J.1971，50（8）：2495-2519.

［2］M.Edelberg，M.R.Garey and R.L.Graham.On the distance matrix of a tree［J］.Discrete Math.1976，14（1）：23-29.

［3］R.L.Graham and H.O.Pollak.On embedding graphs in squashed cubes［J］.Lecture Notes in Mathematics，1972，303：99-110.

［4］R.L.Graham and L.Lovasz.Distance matrix polynomials of trees［J］.Adv.in Math.，1978，29（1）：60-88.

［5］H.Hosoya，M.Murakami，M.Gotoh.Distancepolynomialandcharacterizationofagraph［J］.Natur.Sci.Rep.OchanomizuUniv.，1973，24：27-34.

［6］D.H.Rouvray.The search for useful topological indices in chemistry［J］.Amer.Scientist，1973，61（6）：729-735.

［7］M.Aouchiche.P.Hansen，Two Laplacians for the distance matrix of a graph［J］.Linear Algebra Appl.，2013，439（1）：21-33.

［8］R.A.Horn，C.R.Johnson.Matrix Analysis［M］.Cambridge：Cambridge Univ.Press，1990.

［9］R.Xing，B.Zhou.On the distance and distance signless Laplacian spectral radii of bicyclic graphs［J］.Linear Algebra Appl.，2013，439（12）：3955-3963.

［10］R.Xing，B.Zhou，J.Li.OnthedistancesignlessLaplacianspectralradiusofgraphs［J］.LinearMultilinearAlgebra，2014，62：1377-1387.

［11］G.D.Yu，Q.J.Gong，L.Duan.The distance signless Laplacian spectral radius of trees with n-3 pendent vertices［J］.Journal of University of Science and Technology of China，2014，44（3）：176-180.

［12］X.X.Li，Y.Z.Fan，S.P.Zha.A lower bound for the distance signless Laplacian spectral radius of graphs in terms of chromatic number［J］.Journal of Mathematical Research with Applications，2014，34 （3）：289-294.

［13］李小新，查淑萍.含割点的连通图的最小距离无符号aplace谱半径［J］.中国科学技术大学学报，2014，44（12）：982-985.

［14］K.C.Das.Bounds on the entries of the principal eigenvector of the distance signless Laplacian matrix［J］.Linear Algebra Appl.，2015，483：200-220.

［15］F.L Tian，D.Wong，J，L Rou.Proof for four conjectures about the distance Laplacian and distance signless Laplacian eigenvalues of a graph［J］.Linear Algebra Appl.2015，471：10-20.

［责任编辑：桂传友］

Minimum Distance Signless Laplacian Spectral Radius of Connected Graphs with Cut Edges

Zha Shuping，Li Luyao，Gao Fang
（College of Mathematics and Computer，Chizhou University，Chizhou Anhui 247000）

Among all the connected graphs on n vertices with cut edges，the unique graph with minimum distance signless Laplacian spectral radius is characterized by using the relations of eigenvalue and eigenvector.On this basis，a lower bound of the distance signless Laplacian spectral radius of connected graphs on vertices with cut edges is determined.

Graph；Cut Edge；Distance Signless Laplacian Matrix；Spectral Radius

O157

A

1674-1102（2016）03-0023-03

10.13420/j.cnki.jczu.2016.03.005

2016-03-21

安徽省高校优秀青年人才支持计划重点项目（gxyqZD2016367）；池州学院大学生创新创业训练计划项目（201411306124）。

查淑萍（1978-），女，安徽怀宁人，池州学院数学与计算机学院教师，硕士，研究方向为图论及其应用。