数形结合思想渗透路径

肖文记

数形结合是初中数学重要的数学思想，更是学生解决问题的常用方法。只有以形助数，以数助形，数形渗透，相互作用，才能将复杂的问题简单化，抽象的问题直观化，才能迅速、合理地解决问题，更好地研究数学。笔者在教学中做了如下尝试：

一、透析内容

现行教材中没有明确揭示数学思想，数学思想隐于知识内部，需要反复的研究才能领悟到。如八年级下册《反比例函数的图像和性质》，这节课的内容蕴含了丰富的数形结合思想。首先是画图像，形由数定，自变量x的取值范围为x≠0，它让图像由“一支”变“二支”，形态由“连续”变“间断”；x与y均不为0，它让图像由“相交”变“渐进”，x与y的积为定值，它让图像由“直”变“曲”。由数到形还可以解决画图中的诸多问题。图像的性质应是一个由形到数的过程，如反比例函数的图像分布在一、三象限或二、四象限，不能只让学生画几个图像就归纳总结，应该回归解析式，当k>0时，x与y的符号相同，以（x，y）为坐标的点位于第一或第三象限，且y随x的增大而减小；当k<0时，x与y的符号相反，以（x，y）为坐标的点位于第二或第四象限，且y随x的增大而减小。同时从解析式本身来看，显然图像一定不经过原点，也永远不会与x轴、y轴相交，这种从由形到数的认识，让学生对性质的理解更加科学精准。

二、精细过程

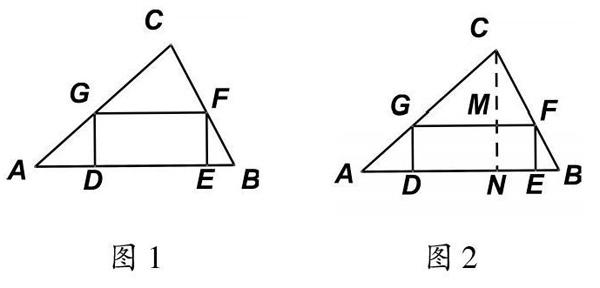
数学思想具有过程性和活动性两个特点，没有过程就没有思想，学生的数学思想是在学习活动中逐步形成的，重在体验与领悟。如武汉市2013年4月调考第24题第3问，如图1所示，在面积为24cm2的△ABC中，矩形DEFG的边DE在AB上运动，点F、G分别在边BC，AC上，请直接写出矩形DEFG的面积的最大值。

笔者以数形结合思想为指导，列出以下任务清单：①给出适当的数据，假设AB=8，GF=2GD，借助图2，你能算出这个矩形的面积吗？②当矩形为正方形时，面积是否会大一些，请你求出正方形的面积。③再换一组数据试一试，令AB=6，内截的正方形面积又会是多少？④对于直接写出答案，你有确定的值吗？⑤如果是解答题，设AB=a，你会建立函数模型求最值吗？以问题引领，让学生自主探究，数形结合的思想悄然渗透于学生思维中。

三、应用拓展

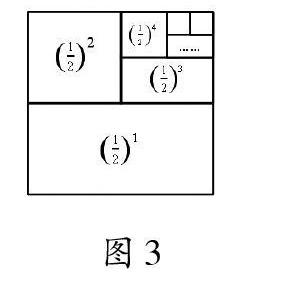
数形结合高层次的表现是“数形互化”。如七年级试题“计算[（12）]1+[（12）]2+[（12）]3+[（12）]4+[（12）]5+[（12）]6”。部分学生选用机械计算，费点工夫也可算对，如果就此作罢，那将毫无思维训练。如果再让学生加一个七次方……结果又是多少，如何描述呢？这时笔者拿出图形，如图3所示，让学生再次感悟数与几何的等量表征，运算不能仅仅停留在数字上，而应结合图形，让枯燥无味的数字变得生动美妙。让学生看图思考，如果将最大的一块面积看作1，那么上述算式的值又是多少呢？学生在数形结合的解题过程中感受到基量的冲撞、数与形的珠联璧合、思维的正反互逆。

四、归纳提炼

数学思想方法具有隐喻性、过程性特点，小结时要结合具体内容去感受和领悟，不要单纯地“贴标签”。

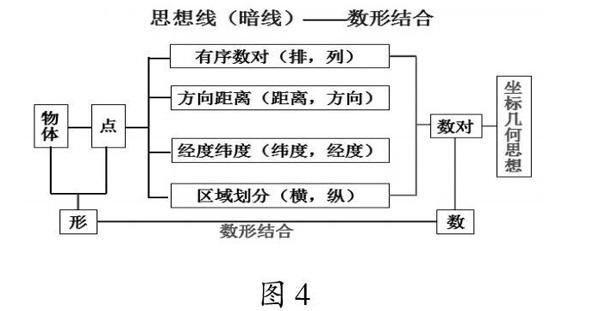
笔者在执教北师大版《数学》八年级上册第五章《确定位置》一课时，如图4所示，利用框图将点的位置与有序数对紧密结合，数学思想不再静水深流，而是重点介绍，一个框图将数学知识、数学技能、数学思想方法融为一体，使思想方法有了载体，知识技能有了灵魂。

在教学中，教师可以通过透析内容、精细过程、应用拓展和归纳提炼来渗透数形结合思想，先要找到数形互助的感觉，并按照数形结合的方法来组织教学，才能让学生真正体验到数学的本质，悟出数形结合思想的真谛。

（作者单位：武汉经济技术开发区第三中学）

责任编辑 孙爱蓉