由数转形，巧解函数难题

柯张军

一、利用函数图像，巧解抽象函数不等式

抽象函数不等式是指没有具体函数解析式的不等式，这类不等式一般利用函数性质求解，画出符合函数性质的草图，观察图形可以直观易解。

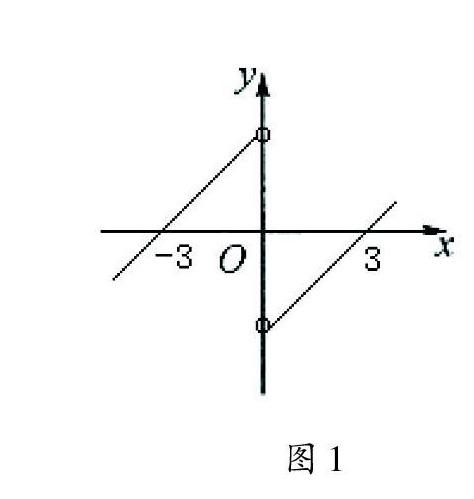
如在求解这道题：设[f（x）、g（x）]分别是定义在R上的奇函数和偶函数，当[x<0]时，[f（x）g（x）+][f（x）g（x）>0][且g（-3）=0]，求不等式[f（x）g（x）<0]的解集时，可以先设[F（x）]=[f（x）g（x）]，因为当[x<0]时，[f（x）g（x）]+[f（x）g（x）]=[[f（x）g（x）]]=[F（x）>0]，所以[F（x）][在（-∞，0）]上是增函数，因为[f（x）、g（x）]分别是定义在R上的奇函数和偶函数，所以[F（x）]为奇函数， 又[g（-3）=0]，所以[F（-3）=f（-3）g（-3）=0]，[f（x）]是奇函数，所以[f（0）=0]，故[F（0）=0]。根据以上特点，不妨构造如图1所示的符合题意的函数[F（x）]的图象，由图直接观察出所求解集是[（-∞，-3）？（0，3）]。

解题过程中依题意确定函数性质，构造函数[F（x）]，依据性质画出[F（x）]草图，观察图像求解，实现抽象问题具体化，复杂问题简单化。

二、利用函数图像，比较数的大小

比较大小是高考试题中一个重要题型，利用函数图形交点位置来确定大小关系，可以避免求值过程中的复杂计算，如果根据题意构造几个函数，画出图像确定交点位置，就可以很快得解。

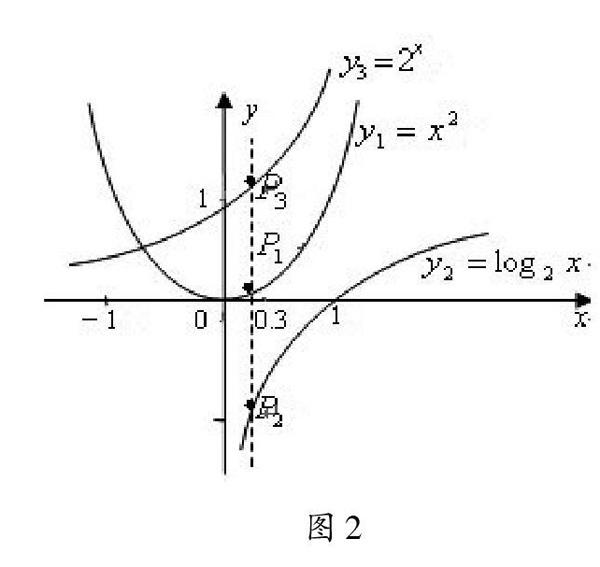
如在判断[0.32，log20.3，20.3]三个数的大小顺序时，可将其看成是三个函数[y1=x2，y2=log2x，y3=2x]在[x=0.3]时，所对应的函数值的大小比较。在同一坐标系内作出这三个函数的图像（如图2），从图像可以直观地看出当[x=0.3]时，所对应的三个点[P1]，[P2]，[P3]的位置，从而可得出结论：[20.3>0.32>log20.3]。

解题过程中三个数的值不易计算，观察数式构造函数，使三个数分别为自变量取同一个值的三个不同的函数值，自然想到三个基本初等函数[y1=x2，y2=log2x，y3=2x]，在同一坐标系中画出三个函数图像作图即可得解。

三、构建解析几何模型，解决函数最值问题

将函数问题转化成解析几何中的斜率、截距、距离等问题，利用其几何意义求解。与解析几何有关的常见函数模型有：①距离型函数[（x-a）2+（y-b）2]；②斜率型函数[y-ax-b]；③截距型函数Ax+By；④单位圆型函数[y=1-（x-a）2+b]；⑤双曲线型函数y=[ax+bcx+d]。

如在求函数[y=x2-2x+5+][x2+6x+25]的最小值时，可以先将函数[y=x2-2x+5+x2+6x+25]变形得：[y=（x-1）2+（0-2）2+（x+3）2+（0-4）2]，由此很容易联想到两点间距离公式，从而使问题转化为求[x]轴上动点[P（x，0）]到两定点[A（1，2），B（-3，4）]的距离之和，结合图3可知：[P，A'，B三点共线即]P点的坐标为[（-13，0）]时，[y]最小，[此时y=213]。

四、利用函数图像，求参数的取值范围

方程根的问题，函数零点问题，图像交点问题，这些问题借助函数图像，往往可以避免繁琐计算，获得简捷的解答。

如在求解这道题：已知方程[1+4-x2] [=kx-2+4]有两个相异实数根，求实数[k]的取值范围时，可以构造函数[y=1+4-x2]与[y=kx-2+4]，方程[1+4-x2] [=kx-2+4]有两个相异实数根等价于函数[y=1+4-x2]与[y=kx-2+4]图像有两个交点，函数[y=1+4-x2]即[x2+y-12=4y≥1] ，它表示以（0，1）为圆心，2为半径的上半圆；函数[y=kx-2+4]表示过（2，4）且斜率为[k]的直线。原题的含义是：当直线与半圆有两个相异交点时，该直线的斜率应在什么范围？如图4，直线MB、MC与半圆切于B、C，半圆的两端依次为A（-2，1），B（2，1）。显然，线段AB内任意一点与M的连线与半圆都只有一个公共点，所以[kmax=kMA=4-12+2=34]，设直线MC交直线[y=1]于N，令[∠DMC=∠DMB=α]，[∠DNM=β]，显然将方程根的个数问题转化为直线与圆交点个数问题，利用几何方法求解直观简单。

（作者单位：黄梅县第一中学）