基于性能退化的动量轮系统故障危害评估*

胡国飞 程月华 杨天社 陆宁云

1. 南京航空航天大学航天学院，南京 210016 2. 西安卫星测控中心，西安 710043 3. 南京航空航天大学自动化学院，南京 210016



基于性能退化的动量轮系统故障危害评估*

胡国飞1程月华1杨天社2陆宁云3

1. 南京航空航天大学航天学院，南京 210016 2. 西安卫星测控中心，西安 710043 3. 南京航空航天大学自动化学院，南京 210016

航天器故障危害评估能够为及时采取预警措施，减少故障在系统内的蔓延，提高航天器的可靠性，以及航天器在轨维修提供重要的理论依据。针对航天器部件故障情况下系统危害评估问题，本文将系统性能退化作为重要影响因素，提出了一种基于故障程度、性能退化特性及历史故障影响程度的故障危害实时定量评估方法，建立了3个影响因素的数学模型及系统故障危害实时定量评估模型。以动量轮系统的2种故障模式验证了所提出方法的可行性和有效性。仿真结果表明，该方法能更加客观地评估航天器部件发生故障时对系统的危害。 关键词 故障模式；影响因素；危害评估；实时；定量

随着航天技术的不断进步，以及对高性能、高可靠性航天器的迫切需求，未来航天器所执行的任务将日趋多样化，航天器的结构将会更加复杂，造价也将越来越昂贵。航天器在轨运行期间，会经历严酷的高温、低温、温度交变、高能粒子辐射、摄动力及电磁干扰等，这些都可能诱发航天器发生故障，同时星上资源有限以及人工干预能力受限，即使是一个微小的元部件故障，都有可能造成航天器无法完成预定任务[1-3]，因此，有必要开展航天器在轨故障危害评估，及时采取预防、预警措施，防止故障危害的蔓延、扩大，提高航天器的可靠性，延长其使用寿命，同时也为航天器在轨维修提供重要的理论依据。

针对部件发生某一故障模式对系统的危害分析研究中，John B. Bowles首先将模糊逻辑运用到故障模式危害评估中，用以描述严重度、发生度和检测度与风险优先顺序的关系，通过引入模糊逻辑克服了传统故障模式危害分析中RPN的缺陷，并提出了2种基于模糊逻辑的危害度评估方法[4-5]。K.Xu等在John B. Bowles的基础上，提出了基于模糊逻辑的故障模式危害评估方法，并对该方法进行了拓展，构建了一个模糊评价系统，通过采用模糊故障模式危害性评估方法对柴油机涡轮增压系统进行风险程度评估，取得很好的效果[6]。Kai Meng Tay等改进了模糊逻辑推理流程，经过改进后的模糊故障模式危害评估方法得到了极大的简化，同时也使进行模糊风险评价的相应规则更加突出[7]。P.A.A. Garcia 等和A Charnes等将模糊逻辑和数据包络分析的思想结合，提出了基于模糊数据包络分析的FMECA方法，该方法一方面能够很好地克服传统FMECA中很难处理“模糊”信息的缺点，另一方面能够借助数据包络分析 (DEA) 模型迅速确定影响每个故障模式的诸多指标的权重，一定程度上降低了评价结果的主观性，使其更加可信[8-9]。康锐等利用模糊数学方法建立模糊FMECA分析模型，对系统或部件进行危害分析，确定其风险程度，找出薄弱环节，给出合理的预防措施[10-11]。Anand Pillay等将灰色理论和模糊规则库应用到传统的FMECA分析中，利用模糊规则库对那些风险程度不同，但是具有相同RPN值的潜在故障模式实施分级，然后采用反模糊语义值与灰色理论确定S，O，D的权重[12]。上述研究成果对开展故障危害分析研究起到了很好的推动作用，但是依然存在不能开展故障危害实时定量评估的问题。

目前，针对航天器开展故障危害评估的研究成果大多是在故障模式影响分析的基础上采用危害矩阵图法和风险优先数法[13-15]。其中，危害矩阵图法是利用不同故障模式的影响严酷度等级绘制系统故障危害矩阵图，分析各种故障模式对系统的危害度，进而为确定处置措施的先后顺序提供依据；风险优先数法是计算不同故障模式的发生概率等级、故障影响的严酷度等级以及故障模式检测难度等级三者的乘积，定量确定不同故障模式对系统的危害度，对引起高危害度的故障模式优先采取处置措施。上述2种方法在开展航天器故障危害评估中，考虑了故障模式的影响严酷度、可检测度以及故障模式的发生概率，是利用专家经验知识以及分析大量历史故障数据得到的，并未考虑故障程度以及部件的性能退化特性因素，而航天器在轨运行期间何时发生故障、以及故障程度的大小是不确定的，由于部件在运行过程中性能不断退化，不同时刻部件的性能状态也不尽相同，因此，针对在轨航天器的故障危害评估中，有必要综合故障程度、部件性能退化特性以及历史故障影响程度这3个因素，开展实时定量的故障危害评估。

本文开展基于性能退化情况下，部件故障对系统的危害评估技术研究，综合考虑部件发生某一故障模式的故障程度、部件性能退化特性以及历史故障影响程度因素，建立了动量轮系统故障危害实时定量评估模型，并针对动量轮系统开展故障危害评估研究，为航天器在轨故障预警及状态维修提供更加准确客观的理论依据。

1 影响因素的数学模型

动量轮系统作为航天器姿态控制的执行机构，主要功能是负责航天器的姿态稳定控制及机动控制，为了提高动量轮系统的可靠性，常采用冗余备份设计。三正一斜装是星载典型动量轮配置系统，3个本体轴上各安装1个性能相同的工作动量轮，斜装动量轮作为3个本体轴动量轮的公共备份。动量轮发生故障时，其故障程度、动量轮性能退化特性以及历史故障影响程度是影响动量轮系统故障危害，实时定量评估的3个重要因素[16]。

1.1 故障程度

故障程度是指部件发生故障，但并未使系统出现功能失效时，部件工作参数偏离正常状态的比值。某一动量轮的工作参数超过正常的允许范围就会使动量轮系统性能下降，进而导致动量轮系统发生功能故障。

考虑动量轮的工作特性并参考相关文献[17]，可以将其重要工作参数的一阶变量，即均值作为衡量动量轮故障程度的评判指标。定义某一轴动量轮发生故障时工作参数的预警值为Dthre，工作参数的阈值为Dl，当某一轴动量轮实时工作参数大于Dthre且小于Dl时，动量轮系统处于故障状态。假设动量轮正常工作情况下工作参数均值为u(u不为0)，动量轮系统运行过程中动量轮工作参数的实测值为m，则动量轮v的故障程度为：

(1)

1.2 性能退化特性

R(t)=P(T>t)

(2)

可靠度是定量评估故障危害的重要指标，借鉴已开展的基于动态故障树卫星姿态控制系统寿命预测研究的相关成果，选取可表征动量轮性能的特征参数(如电流、温度等)，建立性能退化模型[18]，利用历史退化数据得到动量轮在某一工作状态下的失效概率密度函数为fs(t)。动量轮在备份情形下，动量轮未启用前的失效概率密度函数为fn(t)，启用后的失效概率密度函数为fo(t)，得到动量轮在某一工作状态下的失效概率密度函数为：

(3)

其中，ts为动量轮启用时的时刻，tc满足

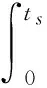
(4)

求解得到动量轮某一工作状态下的失效分布函数为：

(5)

得到动量轮的可靠度函数为：

Rv(t)=1-F(t)

(6)

1.3 历史故障影响程度

历史故障影响程度是指部件历史规定使用时间内所发生的故障模式对系统所造成的影响程度。依据动量轮所发生的故障模式对动量轮系统的影响程度不同进行分类，并给出每一类的评估值，具体见表1。

表1 动量轮故障模式影响程度分类评估表

设有m个专家对动量轮所发生的n个故障模式进行评估，参与评估决策的专家包括设计人员、制造人员以及操作使用人员三类专业技术人员，则有m×n个评估值，用aij来表示，其中，aij表示第i(i=

1,2,3，…,m)位专家对故障模式j(j=1,2,3,…,n)的评估值，则形成m×n的评估矩阵：

对aij进行规范化处理，得到各故障模式的评估值为：

(7)

在n个故障模式的评估值中，存在一个相对最优的评估值，利用算数平均数法可以得到最优评估值λj为：

(8)

利用最优评估值和最小方差理论，得到第i位专家评估值偏差与总评估值偏差的比例ci：

(9)

用βi表示j故障模式因素条件下第i位专家的评估水平：

(10)

综合考虑初始各故障模式的评估值及各位专家的评估水平，采用加权平均的数学模型，得到专家对各故障模式的综合评估值wj：

(11)

在得到各故障模式的综合评估值wj基础上，采用算数几何平均数建立了动量轮历史故障影响程度Dv的数学模型为：

(12)

2 故障危害实时定量评估模型

在开展动量轮系统故障危害实时定量评估的研究中，主要考虑了故障程度、性能退化特性以及历史故障影响程度3个影响因素。故障程度与故障危害度呈正相关，即故障程度越大，其产生的故障危害度越大；历史故障影响程度与故障危害度也呈正相关；当动量轮可靠度越高，发生故障后，其对动量轮系统的危害度越小，即呈负相关。3个影响因素之间存在一定的耦合性，线性的评估模型显然不适用，因此，需要建立非线性评估模型。

为了建立基于多因素的故障危害实时定量评估模型，参考可靠性应用指南中故障模式、影响及危害性分析(FMECA)的研究成果[19]，其主要在考虑影响危害性分析的任务丧失条件概率、故障模式比率、元件失效率以及任务持续时间这4个影响因素的基础上建立了故障模式危害度的定量评估模型，得到故障模式的危害度为：

Cm=β·α·λ·t

(13)

式中，Cm表示故障模式的危害度；β表示功能或任务丧失的条件概率或故障影响概率；α表示故障模式比率，λ表示元件失效率或危害等级；t表示任务阶段持续时间。

因此，可以借鉴文献[18]处理多种因素影响下故障模式危害度的定量评估，建立故障危害实时定量评估的非线性加权模型Θ(v)：

Θ(v)=Θ(Fv,Rv,Dv)

(14)

综合考虑各影响因素的相对重要程度[18]，建立故障危害实时定量评估模型为：

Θ(v) =Fvw1·(1-Rv)w2·Dvw3

(15)

式中，w1表示故障程度的权值，w2表示可靠度的权值，w3表示历史故障影响程度的权值。合理的权重参数是模型能够客观准确地得出评估结果的关键所在，本文将通过层次分析法来确定3个影响因素的权重。下节将以卫星姿态控制系统中的动量轮系统为例开展仿真验证。

3 仿真分析

为了验证所提出的故障危害实时定量评估方法的可行性和有效性，选取三正一斜装的动量轮系统X轴上的动量轮在力矩控制模型下的2种突变故障模式对动量轮系统的危害开展仿真验证，具体步骤如下。

(1)确定X轴动量轮的故障程度

已知某一卫星姿态控制系统正常运行时，其动量轮系统X轴动量轮的相关参数如表2所示，动量轮突变故障的数学模型为：

(16)

式中，Tout为动量轮的实际输出力矩(N·m)；Tin为动量轮的期望输出力矩(N·m)；tf为故障发生时刻；Δt为故障的持续时间。若动量轮发生2种突变故障后的控制电压实测值为f1和f2，通过1.1节的数学模型可以得到这2种故障模式的故障程度Fv。

表2 动量轮相关参数表(单位：V)

(2)确定X轴动量轮的性能退化特性

动量轮在卫星姿态控制系统中有2种工作状态:1)作为工作部件；2)作为备份部件，本文研究的X轴动量轮一直处在工作部件状态下，选取X轴动量轮轴温退化数据，建立性能退化模型[18]，得到其在某一工作状态下的失效概率密度函数为：

得到X轴动量轮的可靠度Rv曲线如图1所示。

图1 X轴动量轮可靠度曲线

(3)确定X轴动量轮的历史故障影响程度

通过对大量同类型同批次动量轮的历史故障模式进行统计，以104h为一个时间段，共统计10个时间段。然后，通过三类专业技术人员对每一个时间段的历史故障影响程度Dv进行评估，具体结果如表3所示。

表3 动量轮历史故障影响程度

(4)确定权值参数

应用层次分析法以及专家经验知识，得到3个影响因素的评判矩阵为：

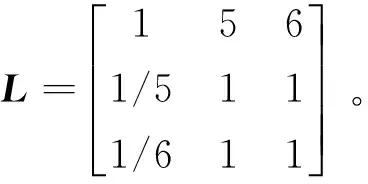
根据评判矩阵，求得最大特征值λmax=3.0940，以及对应的特征向量W，经过归一化处理得到3个因素的权值为：

w0={w1,w2,w3}={0.5217,0.4620,0.0164}。

对所得到的权值进行一致性检测，

CR=0.0810<0.1。

因此，权值的取值是合理的。

(5)仿真结果

将所得到的故障程度Fv、可靠度Rv以及故障影响程度Dv代入故障危害实时定量评估模型中，得到X轴动量轮不同时间发生某一故障模式对动量轮系统的危害度，结果如图2所示。

图2 X轴动量轮故障对动量轮系统的危害度随时间变化曲线

从图2可以看出，X轴动量轮在0～2000h运行阶段，其发生2种故障模式后对动量轮系统的危害度几乎为0，这主要是由于整个动量轮系统性能良好，即使发生一定的故障，可以通过系统的控制，减少部件发生故障后产生的危害；当动量轮运行20000h发生故障后，危害度值会明显增加，同时同一时间不同故障模式对动量轮系统产生的危害也不同，故障模式的故障程度越大，其对动量轮系统产生的危害也越大。对比不同时间X轴动量轮发生同一故障模式，也会产生不同的危害，并且随时间的推移呈现逐渐增大的趋势，这与实际情况是完全吻合的，主要是由于X轴动量轮在运行过程中其性能不断地退化。根据工程经验，选取动量轮系统中等危害阈值为0.3，X轴动量轮运行56000h后发生故障模式1可对动量轮系统产生中等危害，同样X轴动量轮运行89000h后发生故障模式2也可对动量轮系统产生中等危害，动量轮系统处于中等危害的时间点不同，主要是由于部件退化和部件发生某一故障模式的故障程度综合影响的结果。

4 结论

提出了一种基于影响因素的部件故障危害实时定量评估方法，并通过对动量轮系统X轴动量轮的2种故障模式进行仿真分析，验证了所提出方法的可行性和有效性，实现了部件发生某一故障模式对整个子系统危害的实时定量评估，具有一定的理论和工程应用价值。然而，在实际工程应用中，更加关注部件发生故障后对整个系统的危害度，需要考虑部件在整个系统中的结构重要度，以及系统处于不同配置情况下某一部件发生故障对整个系统的危害，这些问题有待后期开展更加深入的研究。

[1] 欧阳高翔，倪茂林，孙承启，李果. 航天器的故障建模与应用[J]. 航天控制, 2011, 29(5):22-29.(OuyangGaoxiang,NiMaolin,SunChengqi,LiGuo.FaultModelingandApplicationofSpacecraft[J].Aerospacecontrol, 2011, 29(5):22-29.)

[2] 南熠. 基于有向图的航天器健康管理算法研究[D].哈尔滨工业大学，2006.(NanYi.ResearchonSpacecraftManagementAlgorithmBasedonDirectedGraph[D].HarbinInstituteofTechnology, 2006.)

[3] 宋飞，秦世引. 卫星姿态控制系统在轨实时健康评估[J]. 北京航空航天大学学报, 2014, 40(11):1581-1588.(SongFei,QinShiyin.Real-timeHealthAssessmentofSatelliteAttitudeControlSystem[J].JournalofBeijingUniversityofAeronauticsandAstronautics,2014, 40(11):1581-1588.)

[4]JohnBBowles,CEnriquePeláez.FuzzyLogicPrioritizationofFailuresinaSystemFailureMode,EffectsandCriticalityAnalysis[J].ReliabilityEngineeringandSystemSafety, 1995,50(2): 203-213.

[5]JohnBBowles,CEnriquePeláez.UsingFuzzyLogicforSystemCriticalityAnalysis[C]. 1994AnnualReliabilityandMaintainabilitySymposium,IEEE, 1994, 449-455.

[6]XuK,TangaLC,XieaM,HoaSL,ZhuML.FuzzyAssessmentofFMEAforEngineSystems[J].ReliabilityEngineeringandSystemSafety, 2002, 75(1): 17-29.

[7]KaiMengTay,CheePengLim.FuzzyFMEAwithaGuidedRulesReductionSystemforPrioritizationofFailures[J].InternationalJournalofQualityandReliabilityManagement, 2006, 23(8): 1047-1066.

[8]GarciaPAA,SchirruR,FrutuosoEmeloPF.AFuzzyDataEnvelopmentAnalysisApproachforFMEA[J].ProgressinNuclearEnergy, 2005, 46(3-4): 359-373.

[9]ACharnes,WCooper,AYLewin,LMSeiford.DataEnvelopmentAnalysistheory,Methodology,andApplication[M].American:KluwerAcademicPublishers, 1997.

[10] 康锐,郑涛.危害性分析中的模糊数学方法[J].北京航空航天大学学报, 1995,21(4): 60-65.(KangRui,ZhengTao.FuzzyMathematicalMethodinHazardAnalysis[J].JournalofBeijingUniversityofAeronauticsandAstronautics,1995,21(4): 60-65.)

[11] 崔文彬,吴桂涛,孙培廷.基于FMEA和模糊综合判断的船舶安全评估[J].哈尔滨工程大学学报, 2007, 28(3): 263-267.(CuiWenbin,WuGuaitao,SunPeiting.ShipSafetyAssessmentBasedonFMEAandFuzzyComprehensiveJudgment[J].JournalofHarbinEngineerUniversity,2007,28(3):263-267.)

[12] 任荣权,于博生,赵众.失效严重度模糊综合评判[J].石油学报,1997,18(2): 138-142.(RenRongquan,YuBosheng,ZhaoZhong.FuzzyComprehensiveEvaluationofFailureSeverity[J].ActaPetroleiSinica,1997,18(2):138-142. )

[13] 张海，周志兵. 故障模式影响分析技术进展[J]. 航空制造技术,2007,8(8):64-66.(ZhangHai,ZhouZhibing.DevelopmentofFailureModeEffectAnalysisTechnology[J].AeronauticalManufacturingTechnology,2007,8(8):64-66.)

[14]PillayA,WangJ.ModifiedFailureModeandEffectsAnalysisUsingApproximateReasoning[J].ReliabilityEnsinecfingandSystemSafety, 2003, 79(1):69-85.

[15]HawkinsPG,WoollonsDJ.FailureModesandEffectsAnalysisofComplexEngineeringSystemsUsingFunctionalModels[J].ArtificialIntelligentEngineering,1998, 12(4):375-397.

[16] 厉海涛. 基于风险状态的安全性分析方法研究[D].国防科学技术大学，2012.(LiHaitao.ResearchonSecurityAnalysisMethodBasedonRiskState[D].NationalUniversityofDefenseTechnology,2012.)

[17] 何克磊. 飞行器健康评估和故障预测技术研究[D].南京航空航天大学，2012.(HeKelei.ResearchonAircraftHealthAssessmentandFaultPredictionTechnology[D].NanjingUniversityofAeronauticsandAstronautics,2012.)

[18] 田静. 基于动态故障树的卫星姿态控制系统寿命预测方法研究[D].南京航空航天大学，2016.(TianJing.ResearchonLifePredictionMethodofSatelliteAttitudeControlSystemBasedonDynamicFaultTree[D].NanjingUniversityofAeronauticsandAstronautics，2016.)

[19] 陈晓彤，赵廷弟，王云飞，吴跃,等.译.可靠性实用指南[M].北京航空航天大学出版社，2005.(ChenXiaotong，ZhaoTingdi，WangYunfei，WuYue，etal.Translation.ReliabilityandPracticalGuide[M].BeijingUniversityofAeronauticsandAstronauticsPress，2005.)

Fault Hazards Assessment of Momentum Wheels System Based on Performance Degradation

Hu Guofei1, Cheng Yuehua1, Yang Tianshe2, Lu Ningyun3

1. College of Astronautics, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China 2. Xi′an Satellite Measurement and Control Center, Xi′an 710043, China3. College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China

Thedevelopmentofspacecraftfaulthazardassessmentcanprovidetimelywarningsmeasurestoreducethespreadoffaultsinthesystem,improvethereliabilityofthespacecraftandprovideimportanttheoreticalbasisforthespacecrafton-orbit-maintenance.Regardingthesystemfaulthazardsassessmentintheconditionofthecomponentsofspacecraftfault,thesystemperformancedegradationistakenasanimportantfactor.Afaulthazardreal-timequantitativeevaluationmethodisproposed,whichisbasedonthreeinfluencingfactorsofthedegreeoffault,performancedegradationcharacteristicsandthedegreeofhistoricalfailureimpact.themathematicalmodelofthethreefactorsandthesystemfaulthazardreal-timequantitativeevaluationareestablished.Thefeasibilityandeffectivenessofthemethodareverifiedbythetwofailuremodesofthemomentumwheelsystem.Thesimulationresultsshowthatthehazardsofthespacecraftcomponentstothesystemcanbemoreobjectivelyevaluatedbyusingthisproposedmethod.

Faultmodel；Influencingfactors；Hazardevaluation；Real-time；Quantitative

*西安卫星测控中心重点实验室基金；南京航空航天大学研究生创新基地(实验室)开放基金(kfjj20160315)

2016-05-30

胡国飞(1990-)，男，山西忻州人，硕士研究生，主要研究方向为系统故障检测与容错控制技术；程月华(1977-)，女，安徽怀宁人，博士，副研究员，主要研究方向为航天器故障预测、故障诊断与容错控制；杨天社(1964-)，男，陕西渭南人，博士后，教授，高级工程师，主要研究方向为航天器系统工程和故障诊断维修技术；陆宁云(1978-)，女，江苏连云港人，博士，教授，主要研究方向为复杂工业过程的建模、监测、故障诊断和质量控制。

V1

A

1006-3242(2016)05-0086-07