控制输入受限的挠性航天器有限时间姿态控制

汪飞舟 贾庆贤 王继河 张德新 邵晓巍

上海交通大学航空航天学院，上海200240



控制输入受限的挠性航天器有限时间姿态控制

汪飞舟 贾庆贤 王继河 张德新 邵晓巍

上海交通大学航空航天学院，上海200240

针对控制输入受限的挠性航天器有限时间姿态控制问题，提出一种将姿态路径优化和终端滑模控制相结合的方法。首先，为了解决控制受限以及挠性附件的振动问题，对航天器姿态机动路径进行了优化设计。其次，基于终端滑模控制思想，设计了一种有限时间控制器，利用Lyapunov稳定性理论证明了挠性航天器姿态控制系统的全局稳定性。最后的仿真结果表明，所设计的姿态控制器不仅保证了挠性航天器能在有限的时间内完成姿态机动，而且对空间环境干扰和挠性附件振动具有较强的鲁棒性。 关键词 路径优化；高斯伪谱法；终端滑模控制；挠性航天器

航天技术的迅猛发展和各种复杂空间任务的需求对航天器姿态机动控制的性能要求越来越高。为了减轻航天器的质量、降低发射成本并提高航天器在轨寿命，现代航天器向越来越轻型化、柔性化的方向发展。现代航天器通常采用中心刚体附带挠性附件的结构，该结构的特点是刚体的姿态运动和附件的振动存在强烈的耦合作用，因此给挠性航天器的控制带来了挑战。另一方面，在轨航天器必然受到各种太空干扰力矩的影响，主要包括重力梯度力矩、太阳光力矩、磁力矩等干扰因素，并且随着燃料的消耗以及挠性附件的振动导致航天器的转动惯量具有不确定性和时变性。因此，挠性航天器的姿态控制系统是一类具有不确定的多输入多输出且具有强耦合作用的非线性系统。

近年来，针对挠性航天器的姿态控制问题，众多国内外学者进行了深入的研究，提出了鲁棒控制[1-2]、滑模变控制[3-4]、以及最优控制[5]等控制策略。Yu 和Meng[6]针对挠性卫星大角度姿态机动控制提出了一种新的鲁棒控制方法，将H∞控制和增益调度控制结合，仿真结果表明该方法降低了保守性且对大干扰具有较强的鲁棒性。Zhong 和Zhou[7-8]等引入了路径规划，并结合了状态反馈控制策略用以抑制挠性附件的振动以提高系统的控制性能。N. singh和Zhang[9]提出了一种新的自适应方法并考虑了系统的未建模动态。S.DiGennaro[10]通过估计航天器的姿态角速度以及柔性模态设计了输出反馈控制策略，但其忽略了模型不确定性和外在干扰的影响。尽管这些方法在某些方面体现了足够的可靠性，但更多的是保证在时间趋于无穷时姿态角误差收敛到0，而现代航天器对于其姿态机动的快速性要求越来越高，许多空间任务要求航天器能在一定的需求时间内完成姿态机动。Zhong和Guo[11]研究了未知干扰下的有限时间挠性航天器姿态控制问题。Wu和Radice[12]基于终端滑模变控制提出了有限时间控制方法，并讨论了系统在模型不确定性和干扰下的鲁棒性问题。终端滑模变结构控制的优点是鲁棒性强，适合处理非线性问题且能在有限时间内收敛，其缺点是存在抖振问题以及为了使系统表现出较强的鲁棒性和更广泛的适应性总是要求执行机构提供足够的控制力矩。然而，在实际航天器控制应用中，通常采用的执行机构(如飞轮、推力器)其输出力矩是十分有限的，既执行机构的输出存在饱和特性，降低了系统的性能，甚至使系统表现出不稳定的特性。因此，研究执行机构输出有限并且具有快速机动能力的挠性航天器姿态控制具有十分重要的理论和工程意义。

针对控制输入受限的挠性航天器有限时间控制问题，本文提出了姿态机动路径优化和终端滑模变控制相结合的控制策略。其中，姿态机动路径优化用以解决控制力矩受限的问题及起到抑制挠性附件振动的作用，路径优化设计通过高斯伪谱法求解得到。在此基础上，基于终端滑模变控制给出了有限时间控制律用以跟踪上述姿态机动路径。最后，将该控制方法用于挠性航天器的姿态机动控制，并进行数值仿真研究。

1 数学模型

挠性航天器的动力学模型由刚体运动方程和挠性附件振动方程组成，可分别表示如下[7]:

(1)

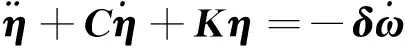
(2)

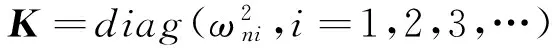
(3)

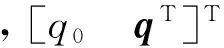
假设1 根据文献[1,5,7],对于挠性航天器的姿态控制系统，通常将挠性附件的振动视作一种外在干扰，即有如下方程成立：

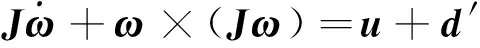
(4)

其中，d′=d+Δ,Δ表示挠性附件引起的扰动力矩，由下式表示：

(5)

其中，ωΔ是由挠性附件振动引起的等效角速度矢量。

2 姿态机动路径优化

挠性航天器姿态控制方法研究大体可以分为2类：1)设计一个闭环反馈控制器；2)跟踪一条优化姿态路径，并结合一个误差反馈控制器。而在实际过程中，特别是在有限的能源和控制输出下，第2种方法显得更具有实际应用价值[1]。另一方面，由方程(2)可以看出挠性附件的振动和刚体的角加速度密切相关，过大的角加速度会激起挠性附件的强烈振动，从而影响姿态控制系统的快速性和稳定性。因此，设计一条平滑的姿态路径可以抑制挠性附件的振动，并解决控制力矩有限的问题。

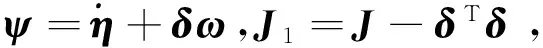
(6)

那么最优姿态路径规划问题就转化为以下目标优化问题：

(7)

其中，a和b分别代表姿态机动时间和能量消耗所占权重比。

并且考虑如下约束：

(8)

其中,umax为最大输出控制力矩。

因此，姿态机动路径优化问题等价于寻找最优控制u*(t)使目标函数J′最小，并且要满足不等式约束条件式(8)以及状态方程(6)。

作为最优控制问题的数值求解方法之一，高斯伪谱法是一种正交计算方法，它的配置点是Legendre-Gauss点。这种方法将状态变量和控制律用多项式参数化，微分方程用正交多项式近似。高斯伪谱法是一种基于谱方法的算法，它比其他方法具有更快的收敛速率。本文采用高斯伪谱法对最优控制问题式(7)求解。该算法的具体原理以及有效性论证参见文献[13]，这里不再赘述。

3 有限时间姿态控制器设计

将设计一个姿态控制器使航天器能在一个给定的有限时间内快速机动地到达指定姿态位置，并且使挠性附件的振动迅速减小直至消失。控制器的设计是基于终端滑模变控制，该控制目标可由下式描述：

(9)

其中，qe为姿态角误差，ωe为姿态角速度误差，T为预先设定的有限收敛时间。

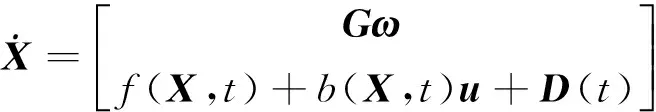
(10)

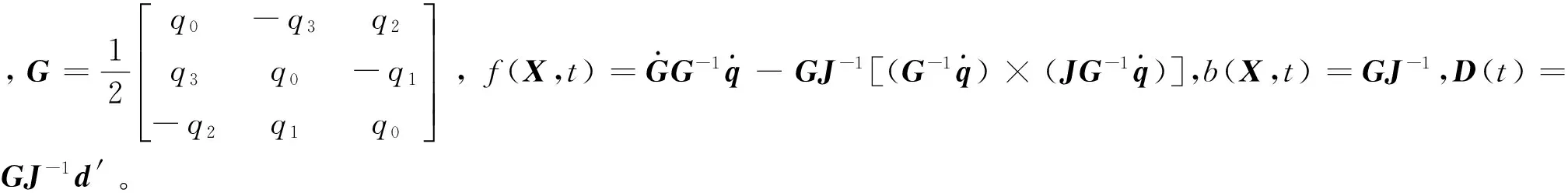
3.1 终端滑模面设计

σ=HE(t)-HP(t)

(11)

这里考虑选取幂级数型函数pi(t)为:

(12)

其中，参数ajl的选择可以通过假设2的条件得到。根据假设pi(t)是一个在t=T时刻二阶可微的连续函数，由此可以得到以下3组线性齐次方程组：

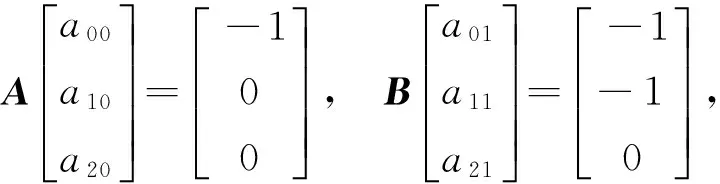
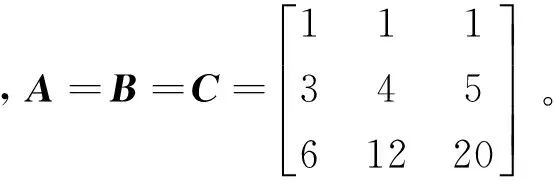
3.2 有限时间控制器设计

在滑模控制中，控制输入应该能迫使系统的所有状态轨迹都收敛到滑模面上，从而保证滑动模态的存在。滑动模态的存在性等价于系统的稳定性，即控制器能使系统从任意初始状态运动到滑模面上最终收敛为0。以下将利用Lyapunov稳定性理论设计控制器。

由滑模面方程式(11)，对其两边求导并结合式(10)可得：

(13)

考虑以下Lyapunov函数：

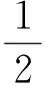
(14)

分别对两边关于时间t求导可得：

(15)

选择控制输入u(t)为:

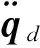
(16)

(17)

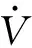
定理1 对于式(10)所示的系统，在假设1的条件下选取式(11)的终端滑模面函数，并采用式(16)的控制策略，可以确保闭环系统的输出跟踪误差能在任意有限的时间内收敛至0。

证明：由式(17)知

(18)

则有

(19)

不失一般性，令矩阵C2=I，则可以得到：

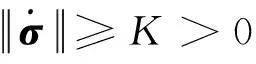
(20)

因此选取足够大的K可以保证滑模面能在有限时间内收敛至0。

证毕。

注2：选取K参数时需要注意，过大的K会导致控制力矩过大，这在实际过程中无法达到，而过小的K又不能保证系统的快速性。

4 数值仿真

挠性航天器动力学模型中的各仿真参数包括系统转动惯量J、刚柔耦合系数矩阵δ、阻尼阵C、刚度阵K和干扰力矩d均取自于文献[6]。

初始姿态为[0.3856,0.5,-0.25,-0.75]T，初始角速度为[0,0,0,0]T，目标姿态为[1,0,0,0]T。假设系统最大输出控制力矩umax=10N·m，控制参数T=20s,k=10。

图1～4为本文设计方法所产生的结果。从图1和2可以看出，姿态四元素在19s左右收敛到稳态值，姿态角速度在20s左右收敛到稳态值，也就说系统状态误差能在给定的预设时间T=20s收敛到0。由图3可以看出控制力矩比较平滑。由图4可知挠性附件的振动得到了较快的抑制，振动幅值较小并且其动态过程平稳，只在机动开始时有一个较大的位移，姿态机动结束后其残余振动较小。

图1 姿态四元素响应

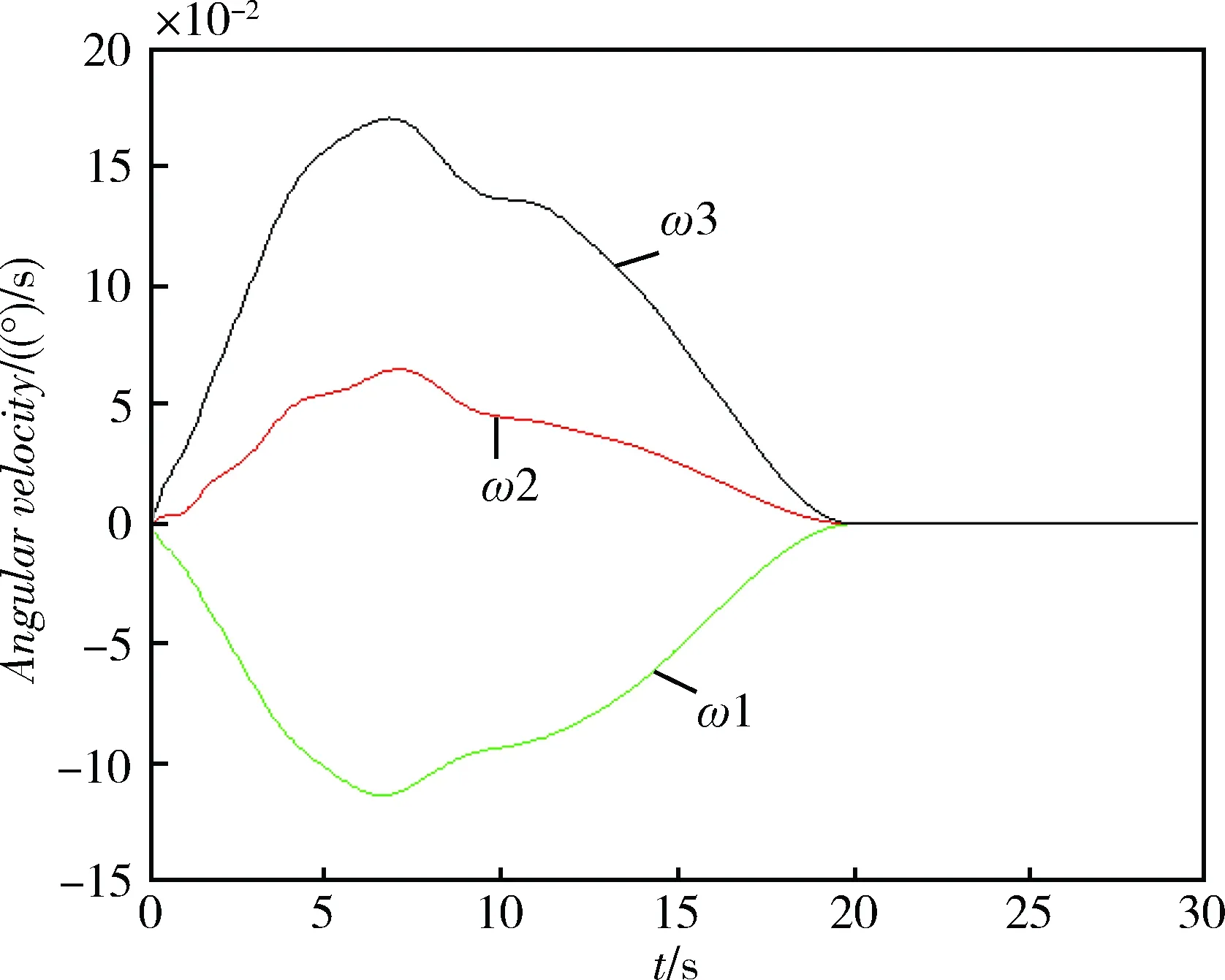
图2 姿态角速度响应

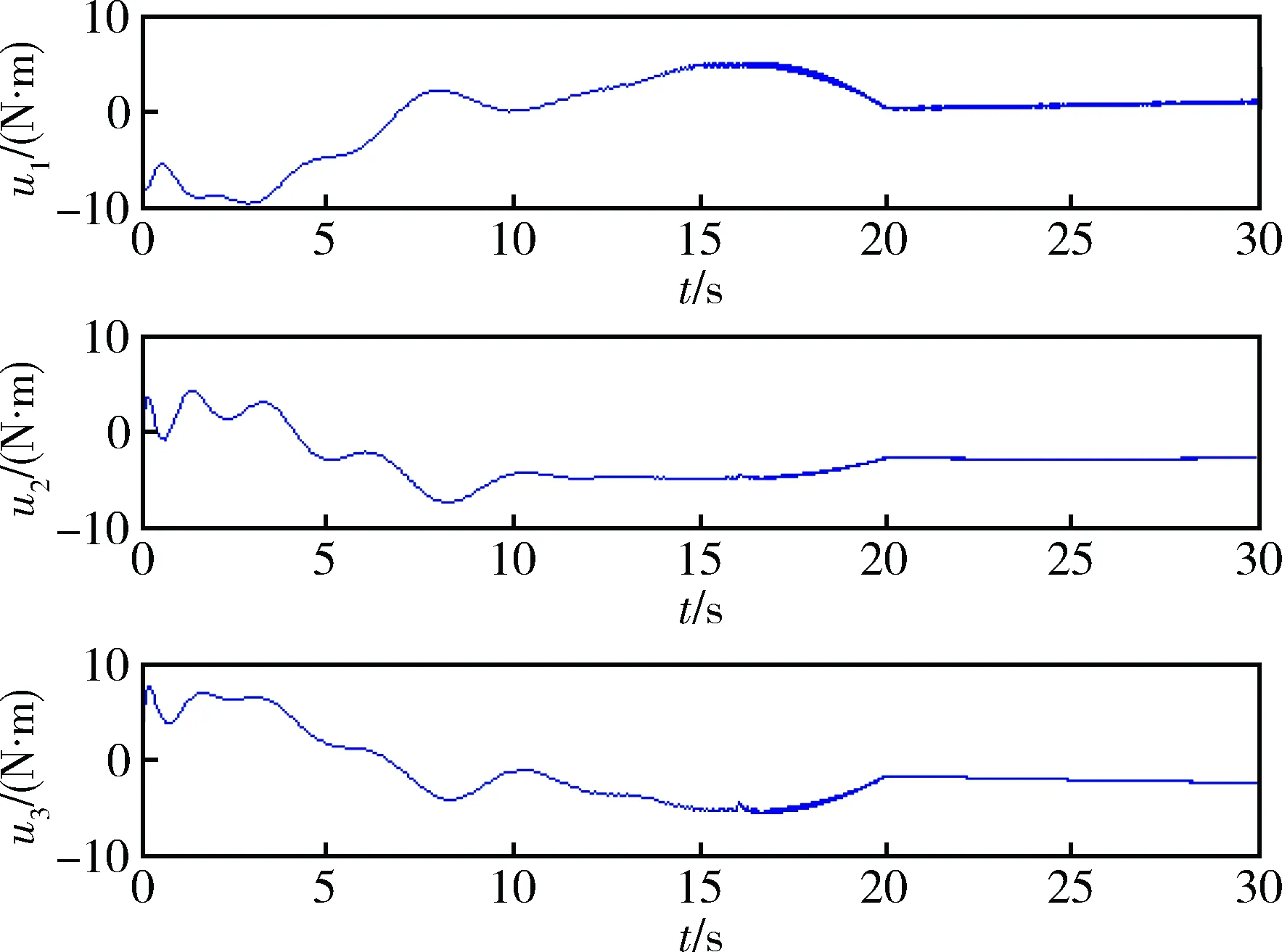
图3 控制力矩

图4 挠性模态

5 结论

针对控制输入受限的航天器快速姿态机动控制问题，本文提出了姿态机动路径优化和有限时间姿态控制相结合的控制方法。路径优化过程能解决控制受限问题，并且能有效抑制挠性附件的振动，使挠性附件振动幅值显著减小，动态过程平稳，且残余振动较小。基于终端滑模变控制的有限时间姿态控制器能使系统误差在任意有限时间至0，并能保证系统的全局稳定性以及鲁棒性。最后，数值仿真结果表明：该方法在控制力矩有限以及干扰力矩的影响下，能有效的抑制挠性附件的振动，使航天器系统能够快速进行姿态机动并稳定。

[1] Cai W, Liao X, Song D Y. Indirect Robust Adaptive Fault-Tolerant Control of Attitude Tracking of Spacecraft[J]. Journal of Guidance, Control, and Dynamics,2008,31(5):1456-1463.

[2] Luo W, Chu Y, Ling K. H-Infinity Inverse Optimal Attitude Tracking Control for Rigid Spacecraft[J].Journal of Guidance, Control and Dynamic, 2005,28(3):481-493.

[3] Hu Q, Ma G. Variable Structure Control and Active Vibration Suppression of Flexible Spacecraft During Attitude Maneuver[J].Aerospace Science and Technology, 2005, 9(4): 307-317.

[4] Crassidis J L , Vadali S R , Markley F L.Optimal Variable Structure Control Tracking of Spacecraft Maneuvers[J]. Journal of Guidance, Control and Dynamics, 2000, 23(3):1456-1463.

[5] McFarland D , Swenson E , Black J , Cobb R. Near Real-Time Closed-Loop Optimal Control Feedback for Spacecraft Attitude Maneuvers[J]. AIAA Paper 2009-5814, Aug,2009.

[6] Yu Ya’nan, Meng Xiuyun, Li Keyong.Robust Control of Flexible Spacecraft During Large-Angle Attitude Maneuver[J]. Journal of Guidance, Control and Dynamics. 2014, 37(3):1027-1033.

[7] Zhong Chenxing, Lai Aifang.On Attitude Maneuver Control of Flexible Spacecraft without Angular Velocity Sensors[C].Proceeding of the 2013 IEEE/SICE International Symposium on System Integration, Kobe International Conference Center, Kobe, Japan, December 15-17: 318-323.

[8] Zhou Chunfeng, Guo Yu, Fu Yanlan. Attitude Control of Flexible Spacecraft Considering Rigid-Flex Coupling Parameters[C]. Proceeding of 2012 International Conference on Modeling, Identification and Control, Wuhan, China, June 24-26,2012,837-842.

[9] Sahjendra n Singh,Rong Zhang. Adaptive Output Feedback Control of Spacecraft with Flexible Appendages by Modeling Error Compensation[J]. Acta Astronautica, 2004, 54:229-243.

[10] Di Gennaro S. Passive Attitude Control of Flexible Spacecraft from Quaternion Measurements[J]. Journal of Optimization Theory and Application, 2003,116(1):41-60.

[11] Chen Xing,Yu Guo, Zhen Yu. Finite-time Attitude Control for Flexible Spacecraft with Unknown Bounded Disturbance[J]. Transactions of the Institute of Measurement and control, 2016,38(2):240-249.

[12] Wu Shunan, Gianmarco Radice, Sun Zhaowei. Robust Finite-Time Control for Flexible Spacecraft Attitude Maneuver[J]. Journal of Aerospace Engineering, 2012, 27(1): 185-190.

[13] 李树荣，韩振宇，于光金.基于高斯伪谱法的最优控制求解及其应用[J].系统科学与数学，2010, 30(8):1031-1043.(Li Shurong,Han Zhenyu,Yu Guangjin.Numerical Algorithm of Optimal Control Based on a Gauss Pseudospectral Method and Its Application[J].Journal of Systems Science and Mathematical Sciences, 2010, 30(8): 1031-1043.)

[14] Kang-Bark Park, Teruo Tsuji. Terminal Sliding Mode Control of Second-order Nonlinear Uncertain Systems[J]. Int. J. Robust Nonlinear Control,1999, 9(11):769-780.

Finite-time Attitude Control of Flexible Spacecraft under Actuator Saturation

Wang Feizhou, Jia Qingxian, Wang Jihe, Zhang Dexin, Shao Xiaowei

School of Aeronautics and Astronautics，Shanghai Jiao Tong University，Shanghai 200240，China

Thefinite-timeattitudecontrolofaflexiblespacecraftunderactuatorsaturationisresearchedbyusingaproposedmethodwhichiscombiningapath-planningmethodwithterminalslidingmodecontrolalgorithm.Firstly,anoptimalattitudepathissuggestedtosolvetheproblemofactuatorsaturationandsuppressvibrationofflexibleappendages.Then,afinite-timecontrollerisdesigned,whichisbasedonterminalslidingmodecontrol,andthestabilityofoverallsystemisprovenbyLyapunovmethodandthefinite-timeconvergenceofthecontrolsystemisalsoproven.Finally,simulationresultsdemonstratethattheflexiblespacecraftisabletocompleteattitudemaneuverinanarbitrarysettlingtimeandhasanidealrobustnesstowardstodisturbancesandflexiblevibration.

Path-planningmethod; Gausspseudospectralmethod;Terminalslidingmodecontrol;Flexiblespacecraft

2015-12-07

汪飞舟(1992-)，男，江西上饶人，硕士，主要研究方向为姿态控制；贾庆贤(1986-)，男，安徽亳州人，博士，主要研究方向为航天器姿态控制、故障诊断；王继河(1982-)，男，黑龙江佳木斯人，博士，主要研究方向为编队/集群飞行构形设计与控制；张德新(1982-)，男，江苏兴化人，博士，主要研究方向为分布式航天器系统仿真技术；邵晓巍(1974-)，男，安徽肖市人，博士，副教授，主要研究方向为航天器导航与控制、系统仿真技术。

V448.22

A

1006-3242(2016)05-0059-05