具脉冲与基因单点突变效应的种群动力学模型

任善静，焦建军,李利梅

(1. 贵州师范学院 数学与计算机科学学院， 贵州 贵阳 550018； 2.贵州财经大学 a.数学与统计学院, 贵州省经济系统仿真重点实验室, b.继续教育学院, 贵州 贵阳 550004)

0 引言

生活在同一空间内的各种动物与植物及微生物相互直接或间接地联系在一起的总体及其生活环境相互作用的自然系统称生态系统.生态系统内通过能量流动和物质循环使环境和生物彼此间联系成统一整体.基因突变在种群耐药性演化中扮演着重要的角色[1].环境污染物可引发基因突变[2].饮水中致突变致癌物的生成及其防治是当今国内外研究的热点[3,4].环境污染物诱发生物体内基因的突变,不仅涉及某一个种,且将引起生态系统内所有种的连锁反应.因为这种突变基因导致生物体内合成的酶蛋白或结构蛋白的变异,最终将引起生物性状的变异.而变异了的种又将影响生态系统内的其他种.

倘若诱发基因突变的污染物浓度较大,则可能同时引起生产者、消费者和分解者多数种类突变.而生物的所有形态及生理特征都是许多基因以及周围环境相互作用的结果.倘若环境污染物促使基因结构和功能变异,必然引起生物机体的形态和功能的改变,从而导致疾病和死亡.例如,一些植物本无毒,原是很多动物的食物.由于基因突变,合成的蛋白变成有毒.这些有毒的蛋白聚集在花粉、叶子或果实上,致使吃食它们的动物成批死亡,引起生态系统内多米诺骨牌效应.据报道:转基因土豆对小白鼠的肾、脾及消化道都造成伤害;转基因玉米“BT玉米”的花粉含有毒素,蝴蝶幼虫啃食撒有这种花粉的菜叶后,发育不良及死亡率很高,在美国艾奥瓦州进行的野外试验亦获得了同样结果.

生物资源是可再生资源，CLARK[5]对可再生资源的管理的经济和生物意义已经有了深刻的阐述.近年来,直接关系到社会可持续发展的生物资源的优化管理被广泛地研究[6].

许多实际问题的发展过程往往具有这样的特性,即系统经历一个短时间的外部作用,但这个短暂的干扰时间同整个的发展过程相比可以忽略不计,所以从数学角度来描述这种发展过程要用到脉冲微分方程.脉冲微分方程是在常微分方程的基础上发展起来的,其突出的特点是能够充分考虑瞬时变化对状态的影响,从而更合理和更精确地反映事物的变化规律.所以许多学者对脉冲微分方程的理论及应用做了广泛的研究.生物种群系统的许多现象都可以用脉冲微分方程来刻画,如动物的季节性出生、渔业养殖和森林管理中的收获、投放和种植等,而且已经形成了较为完整的理论[7-11].

1 模型的建立

基于上面的思路,假设:

(A1)考虑生物体的经济价值,对种群进行脉冲收获.

(A2) 种群的基因突变是不利的,对该种群食物链上的下一级捕食者种群来说是有害的,所以把其突变种群进行脉冲剔除.

(A3) 种群是脉冲出生的,且该种群内部有种内竞争,由于该种群的突变种群是有害突变,故没有考虑种群内部有种内竞争.

(A4) 种群的脉冲出生与该种群的突变种群的脉冲剔除在不同的脉冲时刻发生.

于是建立具脉冲出生与脉冲收获及脉冲剔除的基因单点突变单种群动力学模型:

(1)

其中：x1(t)表示某种群的密度，x2(t)表示其突变种群密度，d11是某种群死亡率系数，d12是某种群种内竞争系数，d21是突变种群死亡率系数，α1表示某种群的突变率且0≤α1<1，α2表示突变种群还原某种群的再现率且0≤α2<1，b1表示某种群在时刻t=nτ的脉冲出生系数，b2表示某种群突变种群在时刻t=nτ的脉冲出生系数，0≤μ1<1表示在时刻t=(n+l)τ收获种群的比例，0≤μ2<1表示在时刻t=(n+l)τ剔除其突变种群的比例,0

2 动力学分析

与

是存在的.显然,系统(1)右边函数的光滑性保证了其解的全局存在和唯一性[7].

由系统(1)的第一与第二个方程,容易得到系统(1)在脉冲点之间的解析解：

(2)

由系统(1)的第三、第四、第五及第六个方程,得到系统(1)的频闪映射：

其中

A1=(1-μ1)(1+(1-α1)b1)d11e-d11τ>0,

A2=(1-μ1)α1b1d11e-d11τ>0,

B=d12(1-e-d11τ)>0,

C1=(1-μ2)α2b2e-d21τ>0,

C2=(1-μ2)(1+(1-α2)b2)e-d21τ>0.

记

于是得到两个等价关系式

Ω>1⟺d11(1-C2)-A1+A2C1-A1C2>0,

与

Ω<1⟺d11(1-C2)-A1+A2C1-A1C2<0.

定理1 i)如果Ω>1,那么方程(3)的不动点G1(0,0)是全局渐近稳定的.

证明为了方便,记

那么差分方程(3)的线性方程可写为：

1-trM+detM>0.

(6)

i)当Ω>1时,即

d11(1-C2)-[A1+A2C1-A1C2]>0

成立,显然G1(0,0)是方程(3)的唯一平衡点,于是

由Jury判据条件

1-trM+detM=

则平衡点G1(0,0)是局部稳定的,进而是全局渐近稳定的.

ii)当Ω<1时,即

d11(1-C2)-(A1+A2C1-A1C2)<0,

那么对于平衡点G1(0,0)有

由Jury判据条件

1-trM+detM=

则平衡点G1(0,0)是不稳定的.

当Ω<1时,即

d11(1-C2)-(A1+A2C1-A1C2)<0,

于是

1-trM+detM=

由定理1,容易得到下面的定理.

定理2 i)如果Ω>1,那么系统(1)的平凡周期解(0,0)是全局渐近稳定的;

(10)

注3 i)当条件Ω>1满足时,系统(1)的种群最终灭绝;ii)当条件Ω<1满足时,系统(1)的种群持续生存,且系统(1)的解有界.

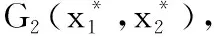
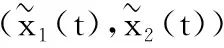
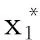
3 讨论