探究高中数学解析几何的多样化解法

毛毳毳

（吉林省松原市长岭县第四中学 吉林松原 138000）

探究高中数学解析几何的多样化解法

毛毳毳

（吉林省松原市长岭县第四中学 吉林松原 138000）

在高中数学教学体系中，解析几何是重要的组成部分，既是教学重点，同时也是教学难点，在开展高中数学解析几何教学过程中，要寻求解题方法的多样性和丰富性，通过寻找不同的解题路径，可以帮助学生构建解析几何知识体系，提升高中数学总体学习水平。本文立足高中数学教学实践，从解析几何具体知识入手，分析解析几何的多样化解决方法。

高中教学 高中数学 解析几何 解法

解析几何是高中数学的重点也是难点，也是训练提升学生逻辑思维和空间想象能力的重要工具，备受高中数学教育工作者的重视[1]。在解析几何学习过程中，往往有多种思考方式，运用综合分析法和体系性分析法，都可以解决问题。在教学实践中，教师要注重利用解析几何知识，激发学生学习自主性和学习自信心，要利用几何知识提升自身数学知识应用水平。

一、多样化解决几何最值问题

在高中数学解析几何学习过程中，最常见的问题是求最值问题，属于高频考点，同时也是学生学习的关键和基础。因此，通过寻求解析几何最值问题的多样化解决途径，可以有效提升高中生解析几何综合应用能力，提高几何教学实效[2]。

1. 充分利用几何图形的对称性特点

在高中数学解析几何解题过程中，应用对称性解题方法，有着深刻的理论依据，当图形两边之差或者两边之和实现三点共线的时候，可以实现其数值的最大化，运用这种思维，可以实现快速高效解题。

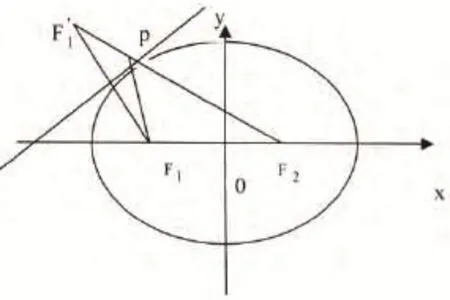
2. 综合利用多种解题方式

除了利用图形的对称性外，还可以应用多种其他方法，解决解析几何最值问题，比较常用的方式是利用圆锥曲线定义方式求解最值问题，通过提取关键信息，实现相关数值的量化和转换，利用已知数值和条件，实现最值问题的有效求解[3]。此外，还可以利用函数值解决解析几何中的具体问题，通过函数法，可以有效提升解析几何问题的解题效率，特别是在最常见的求最值问题当中，应用代数思想，可以将抽象的图像转化为具体的数学公式，进而求解问题。

举例来说，常用的函数解题方法包括二次函数法、均值不等式法等等，都是行之有效的解析几何解题方式，可以实现多样化解题的目的。对于很多数学能力比较强的同学，教师还可以强化教学引导，引导学生利用均值不等式原理，解决解析几何问题。此外，还可以运用距离公式，提升解题效率和解题方式。因此，通过总结以上解题方式，不难看出，要想解决解析几何问题，有着多种多样的方法，最为重要的是掌握其中的原理，进而迅速发现“题眼”，找到解决问题的突破口，实现高效、快速解题，在应用多种方式解决解析几何问题的时候，要仔细分析题意，做到心中有数，选择最为熟练和快速的解题方法，通过反复练习，提升对于解析几何问题的敏感度，提高解题速度，最终实现高中数学学习水平的有效提升，构建自身知识体系。

二、应用三角函数知识丰富解析几何解法

在解决解析几何问题的时候，三角函数知识是重要的突破口和切入点，结合几何问题的特点，利用函数知识，可以实现高速解决。在应用三角函数解决几何问题的时候，还是要根据具体的题目特点，很多时候应用三角函数知识解决解析几何问题并不便捷，但是却可以提供一种不同的思路，对于很多问题，运用三角函数解决是比较方便的[4]。教师在教学过程中，要注重教学引导，学生在选取多样化解题方法之前，首先要了解清楚题干内容和题干要求，真正弄懂问题，根据题目中所考察的知识点，寻找最佳解决方法。

三、应用向量知识解决解析几何问题

在高中数学解析几何问题解决过程中，教师可以引导学生，利用向量知识解决解析几何问题。从知识特点来看，解析结合中的各种元素，包括直线、线段、椭圆、曲线等，都是在坐标轴内呈现，这给向量知识的应用提供了广阔的空间，在解析几何知识结构中，很多几何问题，包括平移、全等、相似等，都可以通过向量知识表现出来，运用向量知识，可以实现解析几何问题的多样化解决。

四、运用数列知识解决解析几何难题

分析各地历年高考题目，很多地方都出现了解析几何知识与数列知识结合的问题，而且都是以最后压轴大题的方式出现，难度较高，具有较高的考试区分度，如果能有效掌握这种解题方法，可以有效提高学生学习层次和考试成绩。在高中数学教学实践中，教师要注重解析几何知识和数列知识的有机结合，从概念、性质等方面入手，寻求知识之间的有效衔接，打通高中数学学习脉络，厘清知识点之间的内在关系，为学生解决解析几何问题提供更多的方式和路径，以提升学生知识应用的灵活程度，提高学生解题能力[5]。如此一来，不管是对于提升学生考试成绩还是知识运用能力，都具有重要意义。

结语

综上所述，在高中数学教学体系中，解析几何是重要的组成部分，学习好解析几何，不仅可以提升学生几何解题能力，更为重要的是，能够锻炼学生的逻辑思维和空间想象能力，切实提高学生的数学水平。在高中数学解析几何教学过程中，教师要注重教学引导，鼓励学生从不同角度思考解析几何问题，通过深入浅出分析，探索多样化的解题方法，实现解题效率的提升，进而构建自身数学知识体系，提高解析几何学习的逻辑性和体系性。

[1]宫前长.关注几何性质唤出简捷解法——例谈解析几何题的几何剖析与教学启示[J].中学数学,2010(10):52-54.

[2]钟水兵.一类高考试题解法探究——解析几何与几何面积的交汇题的处理策略[J].中学数学杂志：高中版,2012(5):58-59.

[3]黄伟军.解析几何中的定点、定值与最值问题解法揭秘[J].广东教育：高中版,2012(1):20-22.

[4]王贵文.一类高考解析几何题的解法探究[J].数学教学研究,2011,30(10):43-44.

[5]过江英.一道意浓的解析几何题[J].语数外学习（数学教育）,2013(6):28-28.