“股灾”时段：融资融券对上证A股市场波动性的影响

吉余峰， 梁 弋， 吉 星

(1.东华大学 旭日工商管理学院， 上海 200051；2.上海财经大学 经济学院， 上海 200433)



“股灾”时段：融资融券对上证A股市场波动性的影响

吉余峰1， 梁 弋1， 吉 星2

(1.东华大学 旭日工商管理学院， 上海 200051；2.上海财经大学 经济学院， 上海 200433)

2015年上证综指一路飙升至最高5 178点，再如过山车般地狂泻至最低不足2 900点，如此巨幅的波动在世界范围内比较罕见。我国自2010年3月31日引入融资融券业务以来，对它的研究一直处于初级阶段，尚不明确其对于我国资本市场的影响究竟如何；造成这次 “股灾”的原因，大部分矛头都指向融资融券业务。本文首次采用全新指标融资融券强度(看多看空系数)，运用T-GARCH与SVAR模型，实证分析了“股灾”时段融资融券对上证A股市场波动性的影响。

上证A股市场； 股指波动性； 融资融券强度； T-GARCH模型

2015年上半年中国股市跌宕起伏，上证市场创出年内新高，指数突破了5 000点大关。在随后的几个月，股指则掉头向下狂泻至最低不足2 900点。为了防止系统性金融危机的发生，政府频频出台政策救市。清理场外配资，禁止大股东大规模套现，严查国内外恶意做空，国家队入场护盘，但似乎所有救市政策的效果都只是昙花一现，仍然阻止不了“股灾”的蔓延。对于造成股指巨幅上扬然后急剧下挫的主要原因，不少专业人士都认为融资融券业务是罪魁祸首，再加上其存在杠杆的特性，使得股指的波动幅度进一步放大，对市场稳定性的破坏更是雪上加霜。它真是股灾的元凶吗？

一、 融资融券与股市波动性关系的文献回顾

由于西方发达国家融资融券业务推出时间比较早，故学术界对融资融券与股市波动性关系的研究比较充分。我国学者只是在近些年才开始此领域的研究。到目前为止，国内外学者在这个问题上大体上存在三种观点。

(一) 融资融券的引入会加剧股市波动性

Bogen和Krooss首次提出融资融券的推出可能加剧资本市场波动性。他们认为，融资融券业务给投资者提供了卖空和买多的投资机会。一旦股票价格出现单向偏离的情形，融资融券业务就会被广泛地使用，从而使得股价偏离程度加大[1]。Allen， Morris和Postlewaite提出了一个有限时期一般均衡模型与信息不对称交换的假设，通过对泡沫时期资本市场的研究，发现卖空机制会引发股市的波动性[2]。蔡笑使用我国台湾市场的月度数据，运用GARCH模型和VAR模型，研究发现融资融券业务的推出使得台湾股市波动性增加[3]。

(二) 融资融券的引入会平抑股市波动性

Angel以纽约股票交易所(NYSE)的144只股票为研究样本，探讨股价下跌是否与卖空交易相关，结果表明常规性买卖指令形成的“助涨杀跌”效应是引起证券市场波动的根源，是加剧市场波动的一个重要原因[4]。Charoenrook和Daouk对多个国家的股票市场进行研究并发现，没有引入融资融券国家的资本市场波动幅度要比引入融资融券的国家小，且两者之间的关系在计量统计层面不是显著的[5]。陈淼鑫，郑振龙针对卖空机制引入后的股市波动情况进行了研究，认为卖空机制的引入一方面会提高股票市场的流动性，另一方面也会减小股市的波动[6]。

(三) 融资融券的引入对股市波动性不产生影响

Figlewski和Webb对标准普尔指数中包含的400多家公司股票进行了实证分析，研究表明卖空和股市波动性之间的相关性并不明显[7]。Battalio 和Schultz研究了纳斯达克市场在互联网泡沫时期的表现，结果发现股市泡沫与卖空机制没有关系[8]。李俊文具体分析了市场波动性与融资融券之间的关系，通过格兰杰检验，发现卖空交易对股市波动性影响不大，反而是股市波动性对融资融券交易的影响较大，往往成为投资者操作的决策依据之一[9]。

二、 研究模型选择

(一) ARCH模型族介绍

1. ARCH模型族

ARCH模型的基本思想是指在以往信息集下，某一时刻一个噪声的发生服从正态分布。该正态分布的均值为零，方差是一个随时间变化的量(即为条件异方差)，并且这个随时间变化的方差是过去有限项噪声值平方的线性组合(即为自回归)。这样就构成了自回归条件异方差模型。

该模型认为，某一时刻噪声项的方差可以由过去多个时刻的有限噪声项的平方回归来表示，从另一个角度可以说明某个时刻噪声的波动程度存在记忆的特点。如果过去多个时刻噪声的方差出现较大的变化，则这种影响会直接作用在未来某一时刻的噪声，同样会引起巨大的变化。同理，如果过去多个时刻噪声的方差出现微小的变化，则这种影响也仍会直接作用于未来某一时刻的噪声，同样会引起微小的变化。

2. GARCH模型

由于ARCH模型自身存在的缺陷，后经Engle的学生T. Bollerslev进一步修正，提出了ARCH模型的一般形式即GARCH模型，通常将其定义为广义自回归条件异方差模型。该模型同样支持异方差随着时间的推移会出现变化的特点。在随后关于股市波动问题的研究中被广泛运用，迄今为止它成为研究波动率中最为理想的模型之一。一般的GARCH模型可以表示为：

(1)

(2)

(3)

其中ht为条件方差，ut为独立同分布的随机变量，ht与ut互相独立，ut服从标准正态分布。(1)式称为条件均值方程；(3)式称为条件方差方程，表明条件方差随着时间的推移会发生变化的特点。

3. T-GARCH模型

Runkle首次提出T-GARCH模型，也称为门限ARCH模型。其数学表达式如下：

(4)

(二) VAR模型

经济计量模型中的变量主要分为两类，一类为内生变量，另外一类为外生变量。但在实际研究中，变量之间的关系难以被清晰地确定或者描述，将两种变量进行划分更是十分困难。如果两种变量存在某种同期相关关系，则将它们区分为内生变量和外生变量是不恰当的，所得出的实证分析结果的说服力也不充分。Sims提出了VAR模型(向量自回归模型)，该模型假设不将变量进行划分，而是将所有变量都作为系统的内生变量进行分析。

VAR模型在建模时，主要考虑两个方面。首先要明确模型中哪些变量之间存在相关关系，然后确定滞后期数。滞后期数的确定主要以AIC准则以及SC准则作为参考依据。VAR(P)模型的数学表达式：

yt=φ1yt-1+…+φpyt-p+Hxt+εt

(5)

其中，yt是k维内生变量列向量，xt是d维外生变量列向量，p是滞后阶数，t是样本个数。k×k维矩阵φ1， …，φp和k×d维矩阵H是待估计的系数矩阵。εt是k维扰动向量，它们之间可以同期相关，但不与自己的滞后项相关，且不与等式右边的变量相关。

三、 融资融券对上证A股市场波动性影响的实证分析

(一) 数据选择与说明

本文选取的数据是上证A股每日收盘指数以及每日的融资融券数据，样本期间是从2014年10月21日至2015年9月30日，总共235个样本数据，此时间段正是上证A股由暴涨至暴跌所处的时间段。

本文选取T-GARCH模型拟合股市波动，并选取条件方差作为股市波动的替代指标；同时计算并引入融资融券强度(看多看空系数)作为解释变量，两个变量的值域在-1到1之间，依次记为MP、SS。融资融券强度计算公式如下：

融资强度=(融资买入额-融资偿还额)/(融资买入额+融资偿还额)

融券强度=(融券卖出量-融券偿还量)/(融券卖出量+融券偿还量)

(二) ARCH效应检验

我们首先对上证A股指数波动性进行ARCH效应检验。为了减少量纲对实证分析的影响，我们对收益率进行对数化处理，并记为lnspt。因为股票价格指数服从特殊的单位根过程，即随机游走模型，回归结果如下：

lnspt=0.984 917lnspt-1+0.125 768

(6)

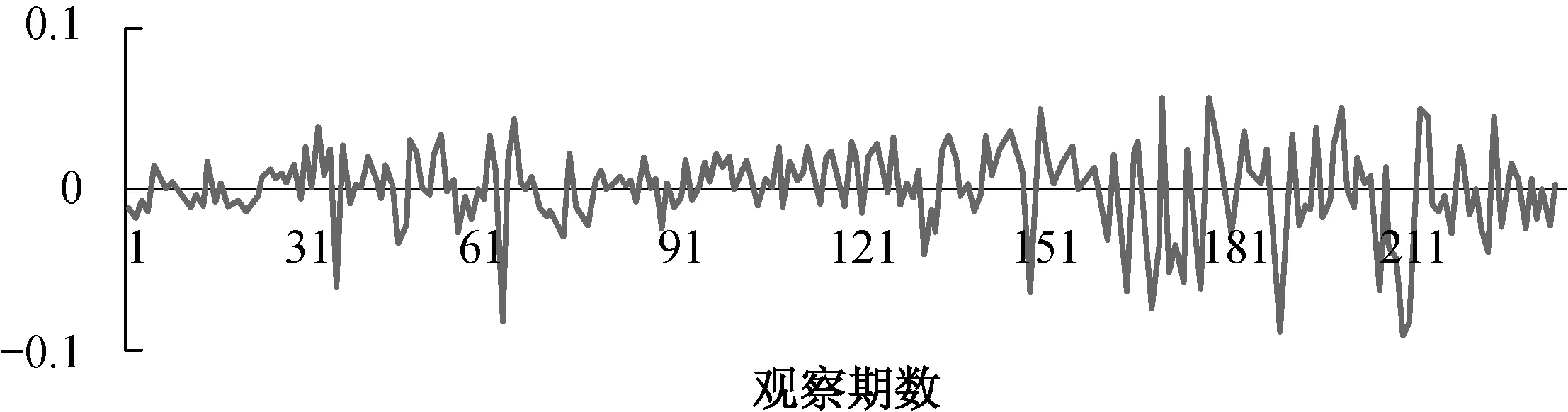
图1 回归方程残差序列

从回归方程的残差序列图中，我们发现波动出现集聚的现象，这说明该序列存在条件异方差性。因此我们对残差序列进行ARCH效应检验，并依据AIC准则来确定检验的阶数。通过1、 4、 8、 12各阶的检验，发现在4阶时，AIC值最小且为-10.649 6，因此确定检验阶数为4。

表1 滞后阶数的AIC检验结果

根据AIC准则，我们选取4阶进行ARCH效应检验

表2 ARCH效应存在检验

从表2中我们可以看出，在5%显著性水平下，拒绝原假设，即存在ARCH效应，因此我们可以采用T-GARCH模型对这一时段的上证A股指数波动性进行拟合。

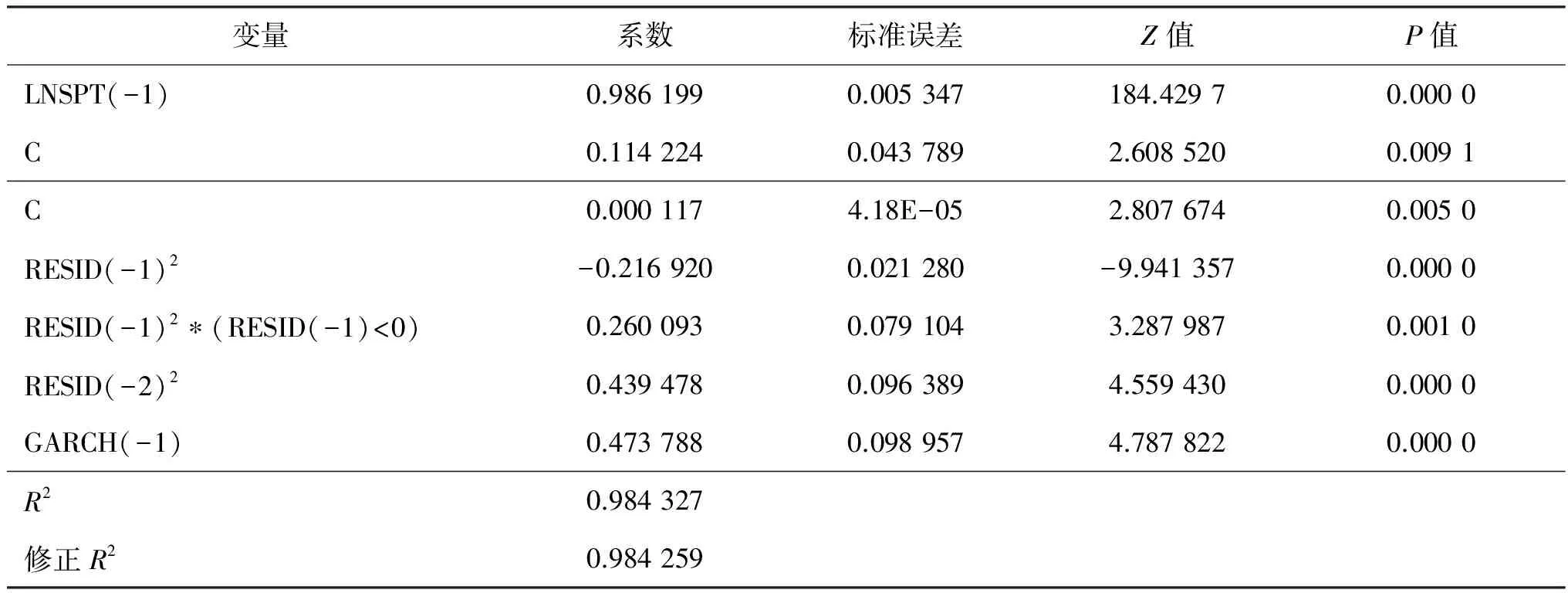
表3 T-GARCH(2.1)回归结果

从表3中我们可以看出，回归方程的R2接近于1，拟合程度较好；非对称项的系数为正值，说明存在杠杆效应，且这种杠杆效应会增加股市的波动性。同时均值方程与方差方程的常数项与系数项在5%的显著性水平都显著，所以回归结果是有效的，此时我们对回归方程进行ARCH效应消除检验。

表4 ARCH效应消除检验

对回归方程进行ARCH效应检验，我们选择之前选定的阶数为2，在5%的显著性水平下，接受了原假设，即不存在ARCH效应。说明T-GARCH模型消除了条件异方差性，因此T-GARCH(2， 1)很好地拟合了这一时段上证A股指数的波动性，我们将提取的条件方差作为股市波动率的替代变量并记为V。

(三) 平稳性检验

我们首先对V、MP、SS三个变量序列进行ADF单位根检验。从下面三个图我们可以看出，三个时间序列都存在截距项，不存在趋势项。

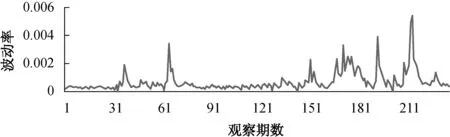
图2 上证A股指数波动率V

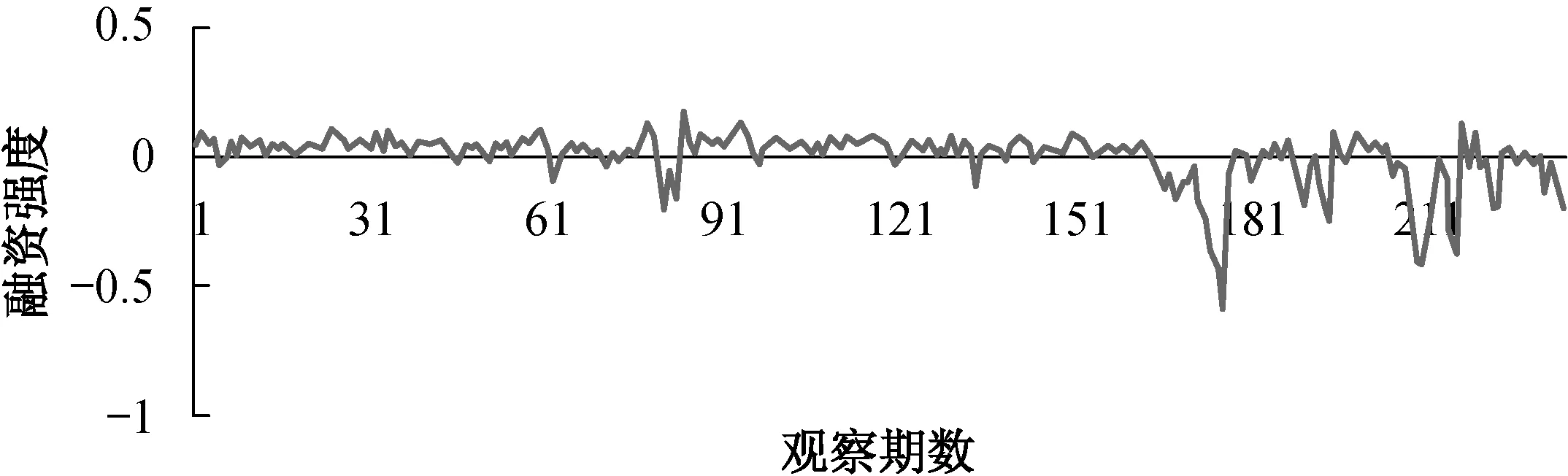
图3 上海股市融资强度MP

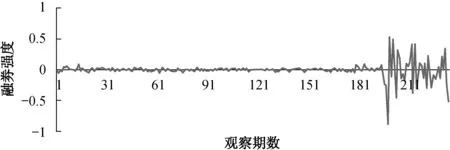
图4 上海股市融券强度SS

表5 ADF单位根检验

单位根检验结果表明，在5%的显著性水平下，均拒绝了原假设，即不存在单位根，V、MP、SS三个序列都是平稳序列。

(四) 三元VAR模型构建

在构建三元VAR模型时，重要的是确定合适的滞后阶数。我们采用EVIEWS 6.0自带的最优阶数选择功能，在指定最高阶数为5阶的情况下，根据不同的准则，每个最优滞后阶数都会标记*符号，选择*符号相对最多的阶数即为最优滞后阶数。如表6所示，我们选择滞后阶数为4阶。

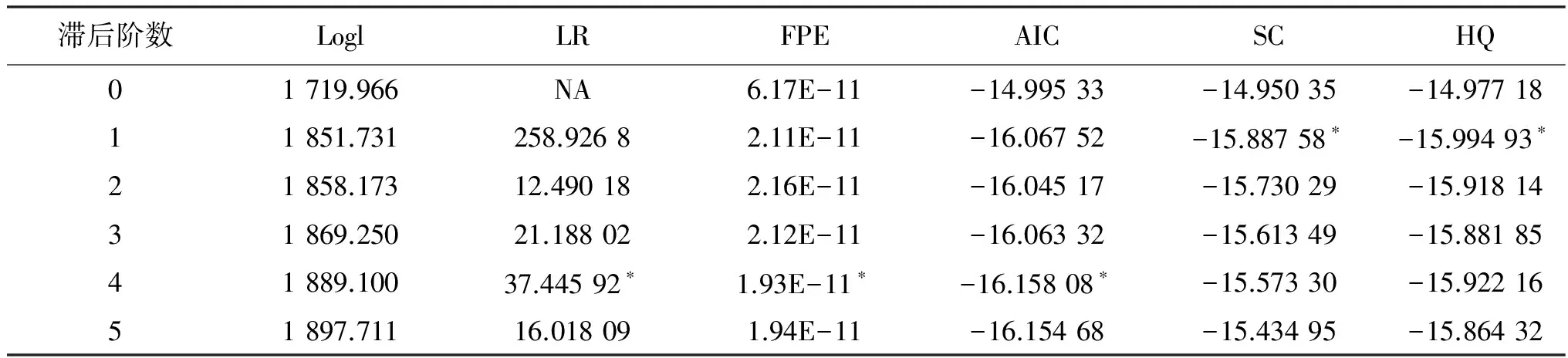
表6 波动率V与融资强度MP、融券强度SS最优阶

在此将V与MP、SS的三元VAR模型定义为VAR(3)。VAR模型估计后，扰动项之间可能存在同期相关关系，而VAR模型无法刻画这种同期相关关系，首先用残差序列的同期相关关系矩阵来描述。用μ1、μ2、μ3来表示三个方程的残差，其结果如表7所示。

表7 相关系数矩阵

从表7中我们可以看出，股市波动率V与融资强度MP、融券强度SS的同期相关系数比较高，但由于VAR模型不能刻画这种同期相关关系，于是采用SVAR模型对其施加短期约束，在此使用A-B型约束矩阵。

对VAR(3)模型短期约束，即对矩阵A、 B进行约束，具体公式如下：

Aεt=But,t=1, 2, 3, …,T

(7)

其中，约束矩阵B是单位矩阵，A矩阵的对角线元素都是1，相当于施加了K2+K个约束条件。对矩阵施加约束，即对变量之间的同期关系施加约束。施加两个约束条件：(1)股市波动率V与当期的融资强度没有关系，即a12=0；(2)股市波动率V与当期的融券强度没有关系，即a13=0。

回归结果：

即：

由此可以发现三个变量之间当期扰动性存在的关系，弥补了VAR(3)的不足。

(五) Granger因果检验

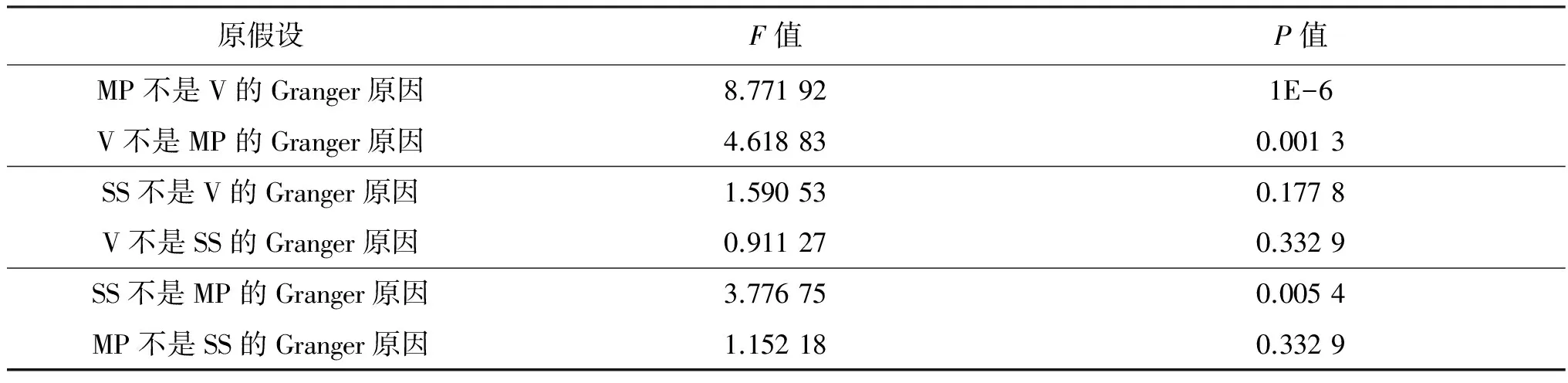
表8 波动率V与融资融券强度MP、SS格兰杰因果检验

从表8中我们可以看出，在5%的显著性水平下，MP与V均拒绝了原假设，表明股市波动率V与融资强度MP互为对方的Granger原因。检验结果说明“股灾”期间融资强度变化还是对上证A股指数的波动率V产生一定影响；同样上证A股指数的波动率的变化也引起了融资强度的变化，这与股市实际运行也是相符的。SS与V均接受了原假设，检验结果表明融券强度的变化不能对股市波动率V产生实质性的影响，可能存在其他原因导致波动率巨幅波动，股市波动率V的变化也不会对融券强度产生实质性的影响。在5%的显著性水平下，融券强度是融资强度的Granger原因，融资强度不是融券强度的Granger原因。说明融券强度的变化也会引起融资强度的变化。

(六) 脉冲响应分析

在对建立的SVAR(3)模型进行脉冲响应分析与方差分解之前，需要确定SVAR模型的稳定性，即AR根都落在单位圆内，表明所建立的SVAR(3)模型稳定。

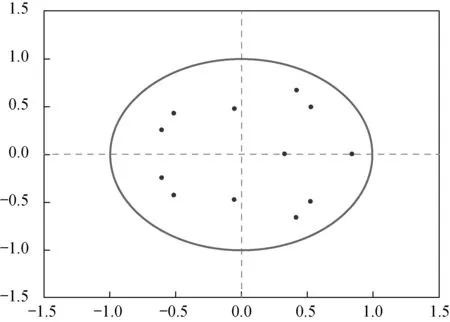
图5 AR根检验结果

当给融资强度MP与融券强度SS一个正向的标准差冲击，作用于股市波动V的脉冲响应结果如图6所示。

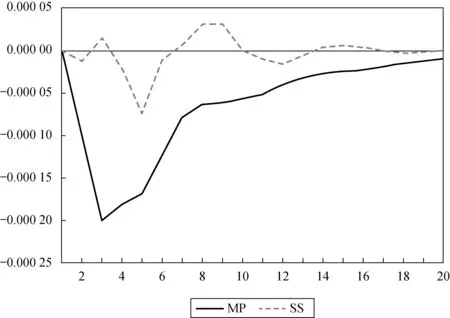
图6 SVAR(3)融资融券强度MP、SS脉冲响应图

从图6中我们可以看出，当给融资强度一个正向的标准差冲击，开始时会对股市波动率V产生一个负向的影响，即减小股市波动。这种影响在第3期时达到最大。随着期数的增加，这种影响在第20期逐渐消失，表明这种影响并不是持久的。在股市拉升阶段，融资强度始终保持在一定的水平，具有降低股市波动的效果。在股市暴跌阶段，融资强度迅速减弱，由于非对称性的影响与杠杆的影响，造成一段时间内股指巨幅波动。反观融券强度，当给融券强度一个正向的标准差的冲击，开始时会对股市波动率V产生一个负向的影响，在第3期又会增加股市的波动，随即在第4期又会对股市波动产生负向的效应，在以后的各期围绕正负向波动，并在第17期逐渐消失，表明融券强度的增强会抑制股市的波动；但这种影响是有限的而且是不可持续的。

(七) 方差分解

在构建三元的SVAR(3)模型基础之上进行方差分解，获知融资融券强度对股市波动率V的解释能力。

从表9我们可以看出，股市波动率V在第20期只有大约71.75%被其自身解释，而相当一部分被融资强度解释掉了，且融资强度解释股市波动的能力随着期数不断增加，在第17期时达到26.64%，且以后各期基本保持稳定。结合方差分解以及条件方差图示来看，股市的巨幅波动主要集中在暴跌阶段，由于存在非对称性的影响，融资强度的急剧减弱给股市造成了极大的波动。证明融资的确是股市巨幅波动的原因之一，融资强度的变化对股市波动产生的影响是很明显的，尤其在其强度减弱的时候，效果更加明显。

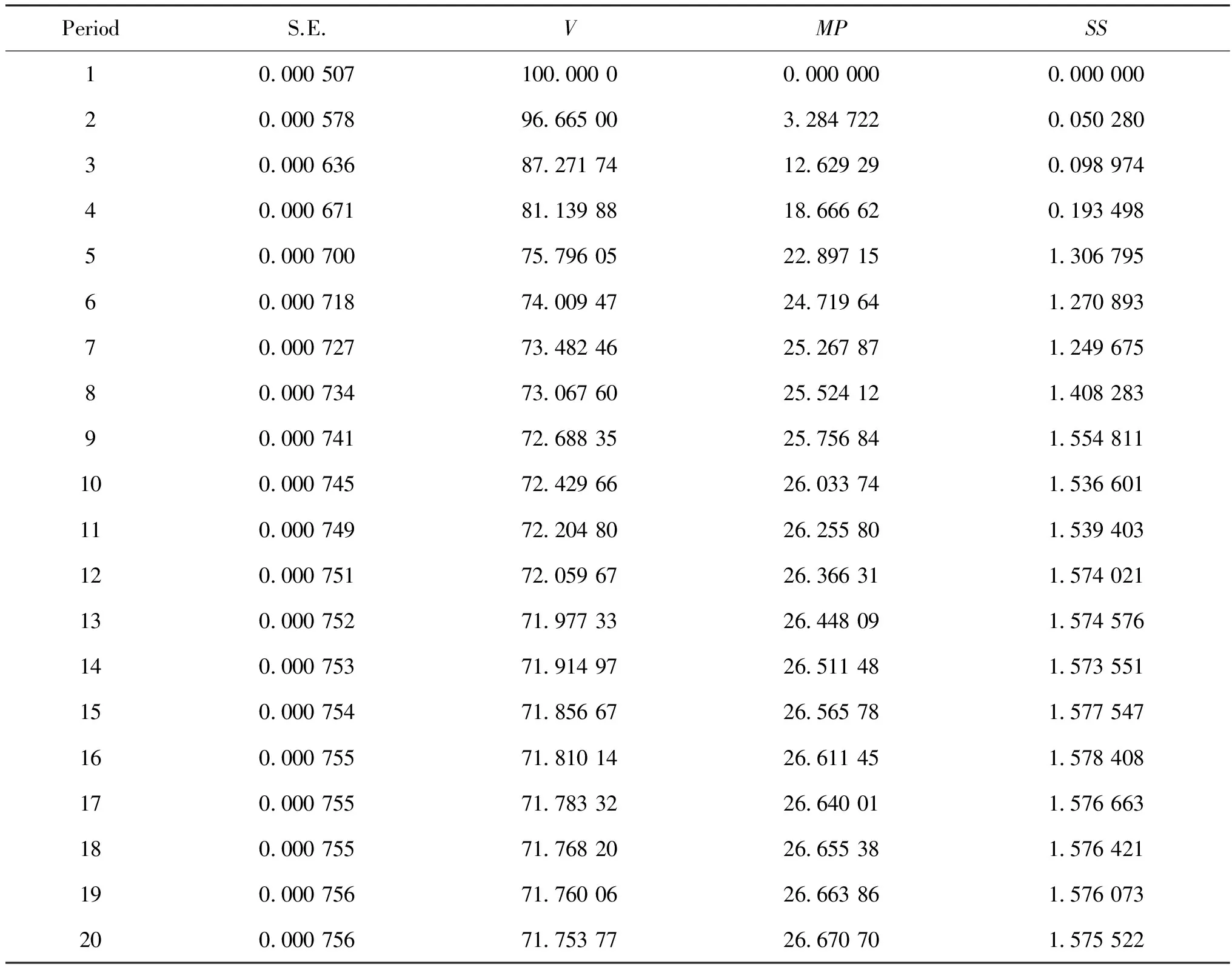
表9 SVAR(3)波动率V的方差分解

反观融券强度，股市波动率V仅有小部分被融券强度解释。融券强度对股市波动率的解释能力随着期数的增加小幅增强，在第12期时达到1.57%，并在随后各期基本保持稳定。方差分解结果表明在股市巨幅波动阶段，融券强度的变化对股市波动的影响是微弱的。

(八) “股灾”时段实证结果分析

第一，导致本轮上证A股指数巨幅波动的主要原因之一便是融资杠杆的使用。由于我国资本市场还处在欠发达阶段，极容易受国家政策性因素的影响，因此融资融券的杠杆特性数倍地放大了风险。股指巨幅上扬的时期，当存在一个来自外界的扰动时，股指有小幅的攀升，投资者追逐短期收益便会加杠杆融资买入，股指成倍数上扬；反过来又会刺激投资者进一步融资买入，如此便形成了恶性循环，造成股指在短短几个月内从3 000点巨幅狂飙至最高5 178点。

第二，我国投资者结构严重不合理。机构投资者占比很小，而个人投资者的比重则非常大，投资策略主要是以投机需求为驱动，追求短期利益，也就是短线投资。大多数投资者缺乏投资理性，易产生跟风和踩踏效应，倾向化严重，容易对股指造成助涨杀跌的作用，极易造成股市的波动。

第三，多空双方规模悬殊。我国鼓励做多不做空，融资融券的规模始终无法平衡，融资的规模要远远超过融券的规模，由此导致券商等金融投资机构无券可融。这种规模的失衡带来的后果便是股市一旦有暴涨，则必有暴跌。在股市急速下跌阶段，融资强度的减弱会造成巨幅的股市波动。根据脉冲响应结果，融券强度增强时会减小股市的波动，如果融券业务的规模与融资强度的规模大体一致的话，可能就不会出现股市暴跌的情形；相反，股市暴涨的情形也会得到遏制。因此融资融券业务规模的不平衡也是股市波动的因素之一。

四、 完善融资融券制度的政策建议

(一) 优化投资者结构

相较于发达国家，我国资本市场仍有待完善，投资者结构有待优化，投资知识、理念有待普及和强化。投资者投资行为大致存在两种模式，一是价值投资，另一种则是投机心理驱动，短期持有或者套利。从各国资本市场的运行历史来看，价值投资是各国资本市场持续、健康运行的重要一环。无论是在保证股市稳定运行，为实体经济发展提供支持，还是在推动资源的分配优化方面都具有深远的意义。西方发达国家投资者结构呈现出多层次的局面，机构投资者的占比较大，而中小投资者的占比较小，这与我国的情况正好相反。机构投资者的投资理念较为合理，投资行为较为成熟，不容易受到其他因素干扰，故大多数机构投资者通过长期持有的方式进行价值投资，因此发达国家极少出现股市波动剧烈的情形。

(二) 适当扩大融券业务规模

我国自引入融资融券业务以来，两者的规模始终处于极不平衡的状态，两融的规模比大致为183∶1。我国资本市场的政策一直是鼓励做多不做空，以保持股票市场持续稳定的上升走势。由此而导致许多证券公司以及其他金融机构经常出现无券可融，或者融券难的尴尬境地。西方发达国家融资融券业务的规模大致相同，并没有出现我国融资融券规模严重不对称的情况。而融资融券规模的不对称所造成的后果就是股市一旦暴涨，就必会有暴跌。本轮A股暴跌也从侧面证实了这一点。如果融券规模与融资规模大致相当，则在股市下跌时，就会起到促使股指下跌软着陆的作用。同样，也就不会出现此轮牛市。融资融券两种业务相辅相成，规模上较大的差距将严重影响两融业务在我国持续健康地发展，同样也会给我国股票市场带来许多负面的影响。融券业务发展不理想的主要原因在于券源不足，机构投资者群体发展不足。成熟市场中，证券出借方主要是长期持有证券的养老基金、保险基金、共同基金等机构投资者，借券目的主要有交割需求、卖空需求、套利交易需求、做市需求等。因此我国股票市场应该通过发展机构投资者的规模，进而带动融券业务规模的扩大。

(三) 加强融资融券账户监管力度

此次“股灾”的发生在某种程度上是由于监管当局对融资融券账户管理的疏松，因此加强账户的管理势在必行。融资融券在实际操作中要比单纯的股票交易复杂得多，监管机构应该充分认识融资融券交易的特点，在对融资融券账户进行管理时，应着重制定若干反映融资融券交易的指标及可容忍范围。当某些指标超过了可容忍的范围或者出现异常的频繁交易，监管当局就可以采取如冻结账户、限制账户的交易额及交易量加以管制，在一定程度上可以控制由融资融券交易所带来的股指波动。

(四) 提升证券监管当局监管能力

此次“股灾”急速下挫及剧烈波动与监管当局“简单粗暴”的干预是密不可分的。证券监管当局应该根据我国的国情，探寻一套适合我国资本市场发展的监督与管理模式。生搬硬套其他发达国家资本市场的监管模式必然是不可取的。我国资本市场大部分是中小投资者，机构投资者则是占少数，市场信心在这样一个市场中是非常重要的。粗暴的、过分的干预只会增加股市的动荡，极易打击市场信心，会导致资金迅速撤离，资本市场流动性大大降低。证券监管当局应时刻观望股市运行情况与投资者情绪，在保证不引起股市巨幅波动以及恐慌的情况下，以适度方式逐步去杠杆。在我国目前的金融市场格局下，证监会应该注意与其他金融监管机构等部门积极协同，方能取得比较理想的监管效果。

[1] Jules Irwin Bogen and Herman Edward Krooss.SecurityCredit：ItsEconomicRoleandRegulation[C]. Englewood Cliffs， NJ：Prentice-Hall， Inc，1960.

[2] Franklin Allen， Stephen Morris and Andrew Postlewaite. Finite Bubbles With Short Sale Constraints and Asymmetric Information[J].Journal of Economic Theory，1993， 61(2)：206-229.

[3] 蔡笑.融资融券对股票市场的影响研究[D].苏州：苏州大学，2010.

[4] James J. Angel. Short Selling on the NYSE [R]. Georgetown University Current Draft， 1997-10-27

[5] Anchada Charoenrook and Hazem Daouk. The World Price of Short Selling [R]. Working paper， The Owen Graduate School of Management， Vanderbilt University， 2003：1-49.

[6] 陈淼鑫，郑振龙.卖空机制对证券市场的影响：基于全球市场的经验研究[J].世界经济，2008，(12)：73-81.

[7] Stephen Figlewski and Gwendolyn Webb. Options， Short Sales， and Market Completeness [J].JournalofFinance， 1993， 48(2)：761-777.

[8] Robert Battalio and Paul Schultz. Options and the Bubble [J].JournalofFinance，2006，61(5)：2071-2102.

[9] 李俊文.我国融资融券交易对市场波动性影响的实证分析[J].中国证券期货，2011，(12)：43-47.

[10] 曾长虹.涨跌幅限制对流动性和波动性影响的因子分析[J].金融研究，2004,(4)：37-44.

[11] 瘳士光，杨朝军.卖空交易机制对股价的影响——来自台湾股市的经验证据[J].金融研究，2005,(10)：131-140.

[12] 高铁梅.计量经济分析方法与建模[M].北京：清华大学出版社，2009.

[13] 黎元奎.建立我国股市融资融券制度的动因分析与模式选择[J].武汉金融，2004，(5)：37-40.

[14] 李谦.融资融券业务对资本市场的影响[J].中国金融，2009，(5)：72-73.

[15] 廖士光，杨朝军.证券市场中卖空交易机制基本功能研究[J].证券市场导报，2005，(3)：72-77.

[16] 文艳军.融资融券对我国股票市场的影响研究[D].成都：西南财经大学，2012.

[17] 张晓峒.EViews使用指南与案例[M].北京：机械工业出版社，2007.

[18] 赵振全，张宇.中国股票市场波动和宏观经济波动关系的实证分析[J].数量经济技术经济研究，2003，(6)：143-146.

2016-10-10

吉余峰(1966—)，男，江苏南通人，副教授，博士，研究方向为资本市场。E-mail:jiyufeng66@126.com

F832.5

A

1009-9034(2016)04-0231-10