BFA-CM最优化测井解释方法
潘保芝, 段亚男,2*, 张海涛, 杨小明, 韩雪
1 吉林大学 地球探测科学与技术学院, 长春 130061 2 辽宁省物测勘查院, 沈阳 110121 3 中国石油 长庆油田勘探开发研究院, 西安 710021 4 胜利石油工程有限公司 测井公司一分公司, 山东东营 257200
BFA-CM最优化测井解释方法
潘保芝1, 段亚男1,2*, 张海涛3, 杨小明3, 韩雪4
1 吉林大学 地球探测科学与技术学院, 长春130061 2 辽宁省物测勘查院, 沈阳110121 3 中国石油 长庆油田勘探开发研究院, 西安710021 4 胜利石油工程有限公司 测井公司一分公司, 山东东营257200
摘要最优化测井解释方法能充分利用各种测井资料及地质信息,可以有效地评价复杂岩性油气藏.优化算法的选择是最优化测井解释方法的关键,影响着测井解释结果的准确性.细菌觅食算法(BFA)是新兴的一种智能优化算法,具有较强的全局搜索能力,但在寻优后期收敛速度较慢.复合形算法(CM)局部搜索能力极强,将其与BFA算法相结合构成BFA-CM混合算法,既提高了搜索精度又提高了搜索效率.利用BFA-CM最优化测井解释方法对苏里格致密砂岩储层实际资料进行了处理,计算结果与岩心及薄片分析资料吻合得很好.
关键词细菌觅食算法; 最优化; 测井解释; 复合形算法; 混合算法
1引言
最优化测井解释方法是20世纪80年代初发展的新技术,它将所有测井信息、测量误差和响应方程误差以及某些地质经验综合成一个多维信息复合体,应用最优化数学方法进行多维处理,求解出该复合体的最优解(雍世和,1995).最优化数学方法的选择是最优化测井解释方法中的关键,关系到测井解释结果的准确性.最优化测井解释的目标函数复杂,以梯度为基础的传统算法不能满足这个要求.自20世纪70年代以来,诞生了一系列以仿生学为基础的群智能优化算法,也称“启发式算法”,包括遗传算法、蚁群优化算法、粒子群优化算法和细菌觅食算法等(刘小龙,2011).
细菌觅食算法(Bacterial Foraging Algorithm,简称BFA)自Passino(2002)提出以来引起了各领域专家的重视,该算法以及其改进算法被广泛应用于车间调度、工业仪器设计、图像压缩及预测控制等实际问题中,并取得了良好的应用效果(Tripathy et al.,2006;张娜,2007;Kim and Cho,2005,2006; 储颖等,2008).迄今为止,BFA算法还未被应用于最优化测井解释中.复合形算法(CM)是一种具有极强局部搜索能力的优化算法,由勃克斯(M.J.Box)于1966年改进单纯形算法而来,在机械工程领域应用广泛(张晓洪等,2003).韩雪(2012)将复合形算法与遗传算法相结合应用于砂砾岩最优化测井解释中,计算结果精度较高.
苏里格地区岩性成分复杂,孔隙结构多样,造成常规测井解释方法求取储层参数困难(王翠平,2013).最优化测井解释方法可以有效地评价复杂岩性储层,但其目标函数复杂,对优化算法要求较高.许多学者选择运用混合优化算法求解地球物理反演问题,如谭茂金和邹友龙(2012)将混合优化算法用于油气储集层二维NMR(Nuclear Magnetic Resonance,核磁共振)测井的反演和流体识别,巩思园等(2012)应用混合优化算法定位煤矿矿震震源位置,罗明秋等(2003)将混合优化算法应用于三维隐式方法偏移.本文首次引入BFA算法解决最优化测井解释问题,并将其与复合形算法(CM)相结合构成BFA-CM混合算法应用于苏里格地区.
2BFA-CM算法基本原理及其实现流程
2.1细菌觅食算法(BFA)
细菌觅食算法(BFA)以微生物为模仿对象,模拟了大肠杆菌在人体肠道内通过鞭毛不断游动寻找食物的行为.研究发现,当细菌所处环境中食物不足时,该细菌会随机选择一个方向移动,如移动后食物丰富则继续向该方向前进,如移动后食物状况未改善,则重新随机选择方向继续寻找.细菌的生存遵循达尔文的“适者生存”的理论,只有那些能量高的细菌可以分裂产生新个体,细菌能量低的个体则会死亡(尤梦丽和雷秀娟,2013).
细菌觅食算法通过趋化、繁殖和迁移3个操作算子迭代寻求最优解(刘小龙,2011).
(1) 趋化算子:在趋化过程中,细菌是通过翻转和游动两个基本动作向食物密集区靠近的.翻转是指细菌改变方向并移动单位步长的动作,细菌翻转后若适应值得到改善,则继续沿该方向移动若干步,直到适应值不再改善或者达到规定阈值Ns为止,这一过程即为游动.
设P(i,j,K,ell)表示第i个细菌、第j次趋化循环、第K次繁殖循环、第ell次迁移循环的位置,则趋化过程中细菌位置的改变可表示为
P(i,j+1,K,ell)=P(i,j,K,ell)+c(i)Deita(i),
(1)
其中,c(i)为移动方向上移动的步长向量,Deita(i)为随机产生的方向向量.
(2) 繁殖算子:设定趋化周期Nc为细菌的一个完整生命周期,当细菌完成一个生命周期后,细菌进入繁殖阶段.繁殖阶段体现了达尔文“适者生存”的理论,将一个生命周期内每个细菌的适应值J(i,j,K,ell)累加和作为细菌的能量Jhealth(i).将S个细菌按能量由大到小进行排序,能量较大的前Sr=S/2个细菌保留下来,并且其中每一个细菌复制成两个细菌,能量较小的后Sr=S/2个细菌死亡.繁殖过程结束后,细菌总数保持不变.
(3) 迁移算子:为避免细菌种群多样化退减,迁移算子模拟了细菌随水流迁移到新环境的生物现象.繁殖循环后,算法会随机生成一个概率p,如果生成的随机概率p小于预先设定的迁移概率Ped,所有细菌将被随机分配到空间内任意位置.迁移算子可以提高算法的全局搜索能力,防止算法陷入局部极值点.
2.2复合形算法(CM)
利用复合形算法求解优化问题时,需要在一个n维空间内建立一个k个顶点的复合形.图1为复合形算法示意图(n=2,k=3).复合形算法以目标函数值大小评价顶点的好坏,目标函数值最大的点为最差点,目标函数值最小的点为最好点.建立好初始复合形后,需要计算F1、F2、F3三个顶点的目标函数值,假设计算后目标函数值由大到小的点依次为F3、F2、F1,去除最差点F3,以剩下F1、F2两点的质心为映射中心寻找到所去除最差点F3的映像点Fr,以映像点Fr代替之前的最差点F3构成新的复合形.以这种方式不断迭代,复合形不断缩小,当复合形各个顶点的质心与各顶点充分接近时,迭代停止,将此时复合形顶点中目标函数值最小的点输出,作为最优解(韩雪,2012).
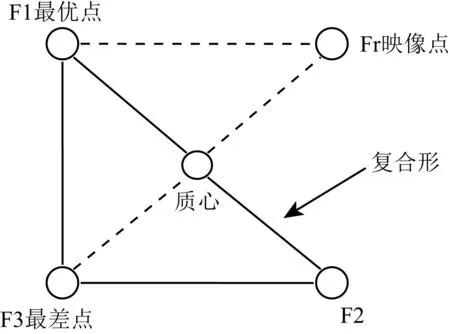
图1 复合形算法原理示意图
2.3BFA-CM混合算法的实现流程
研究结果表明,BFA算法在搜寻最优解的后期收敛速度变慢(张璨,2013).CM算法不需要求取目标函数导数,且可以避免迭代过程中的退化现象,具有极强的局部搜索能力.将BFA算法和CM算法相结合构成BFA-CM混合算法,融合方式简单,且运行效率高.图2为BFA-CM混合算法的流程图,将BFA算法计算的初步优化结果作为CM算法的初始值之一进行二次优化,其具体实现步骤如下:
(1)参数初始化,包括:
①细菌觅食算法:趋化次数Nc、游动次数Ns、繁殖次数Nre、迁移次数Ned、细菌个数S、迁移概率Ped;
②复合形算法:顶点个数k.
(2)初始化细菌位置,并计算每个细菌的适应值J(i,j,K,ell).
(3)通过趋化、繁殖和迁移3个操作算子在三层循环中迭代寻求最优解.三层循环中,最外层的是迁移循环,中间的是繁殖循环,最内层的是趋化循环.趋化循环过程中执行趋化算子,通过翻转和游动两个基本动作更新细菌位置;趋化循环结束后,进行繁殖算子;繁殖循环结束后,进行迁移算子.
(4)细菌觅食算法寻优过程结束,输出初步最优解pbest.
(5)将细菌觅食算法寻求的最优点pbest作为复合形的初始顶点之一,并初始化复合形其余各顶点;
(6)计算复合形初始各顶点的目标函数值,得到最好点、最坏点及形心;
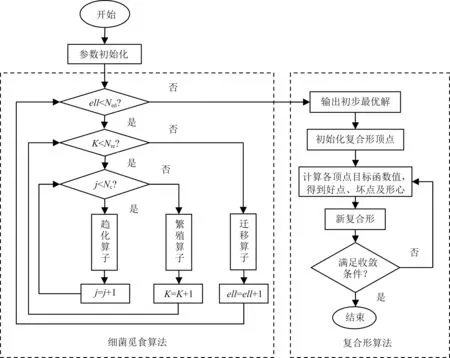
图2 BFA-CM混合算法流程图
(7)计算映射点并构成新复合形;
(8)循环结束条件判断.若不满足则返回步骤(6);若满足则迭代终止,输出结果.
3BFA-CM最优化测井解释方法
3.1最优化测井解释基本原理
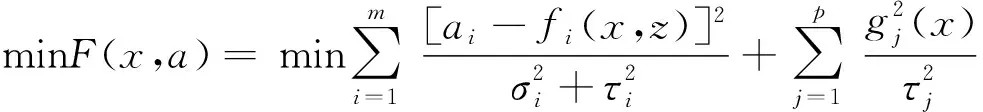
(2)
式中,m为参与计算的测井曲线数量;σi为各种测井方法在测量过程中的测量误差;τi为解释模型引起的响应方程误差;p为约束条件个数;gj(x)和τj分别为第j个约束条件及约束误差.
3.2数学模型的建立
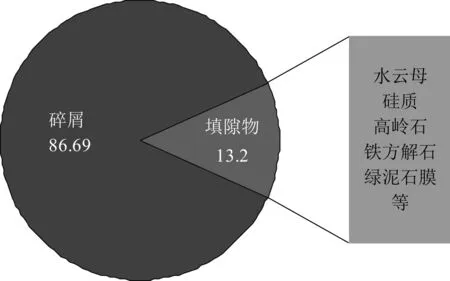
图3 岩石组分饼状图

图4 碎屑成分饼状图
针对苏里格致密砂岩储层岩性复杂的特点,本文选择多组分模型作为该地区的测井解释模型,将地层看作是由局部均匀的几部分组成(田云英和夏宏泉,2006).图3、图4为苏里格气田盒8及山1层段岩石组分饼状图和碎屑成分饼状图.储层碎屑成分以石英类为主,岩屑次之,长石类含量极少.岩屑主要包括千枚岩、变质砂岩、片岩和隐晶岩等.填隙物的主要成分为水云母、硅质和高岭石等黏土类矿物.为简化模型,本文假设孔隙中的流体只有水,对研究区建立图5所示的多组分模型,将地层视为由水、泥质、石英、岩屑4部分组成,φ、Vcl、Vma1、Vma2分别为这4个组分的体积含量.
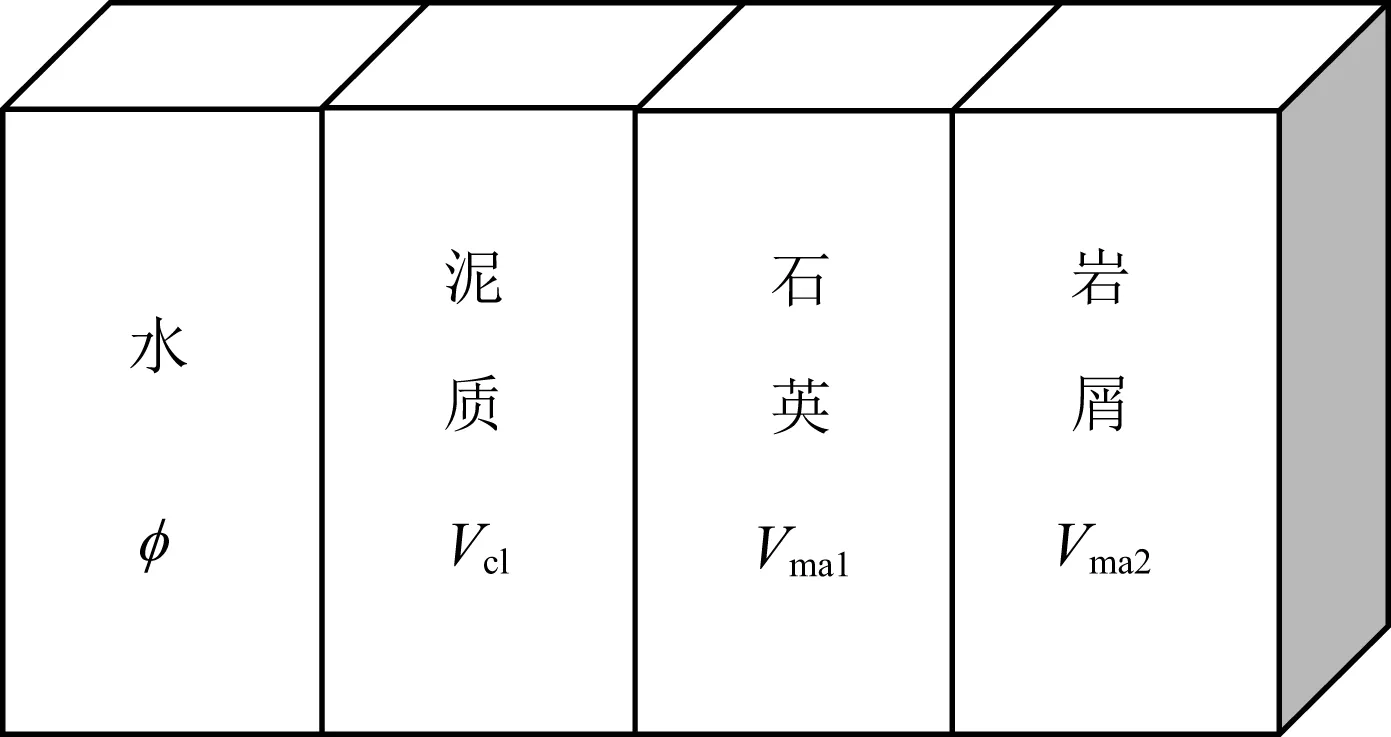
图5 多组分模型示意图
3.3测井响应方程的建立
根据该地区所建立的多组分模型确定测井响应方程.由于用BFA-CM混合算法作为最优化测井解释的优化算法,方程的个数和未知量的个数不做严格要求.待求的储层未知量个数为4,本文选择参与计算的响应方程个数为3,分别为密度测井DEN、声波测井AC、中子测井CNL.它们的测井响应方程可以表示成如下形式:
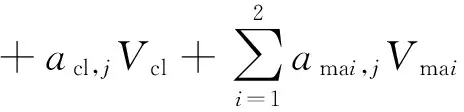
(3)
式中,j=1、2、3分别表示密度、声波及中子测井方法;Mj表示第j种测井方法的实际测量值;af,j表示孔隙流体对第j种测井方法的响应值;acl,j表示泥质对第j种测井方法的响应值;amai,j表示第i种骨架组分对第j种测井方法的响应值.
3.4解释参数的确定
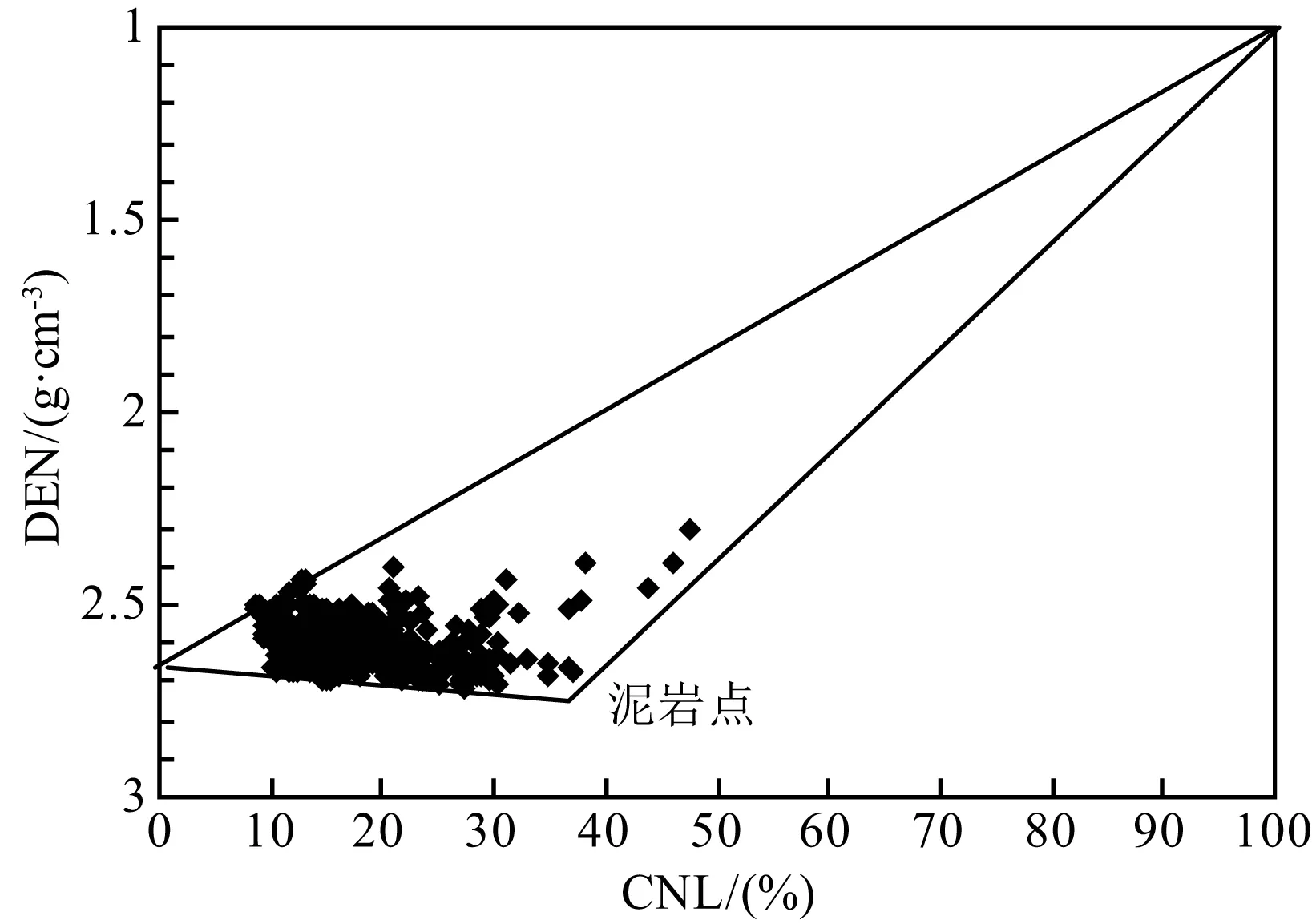
图6 中子-密度交会图
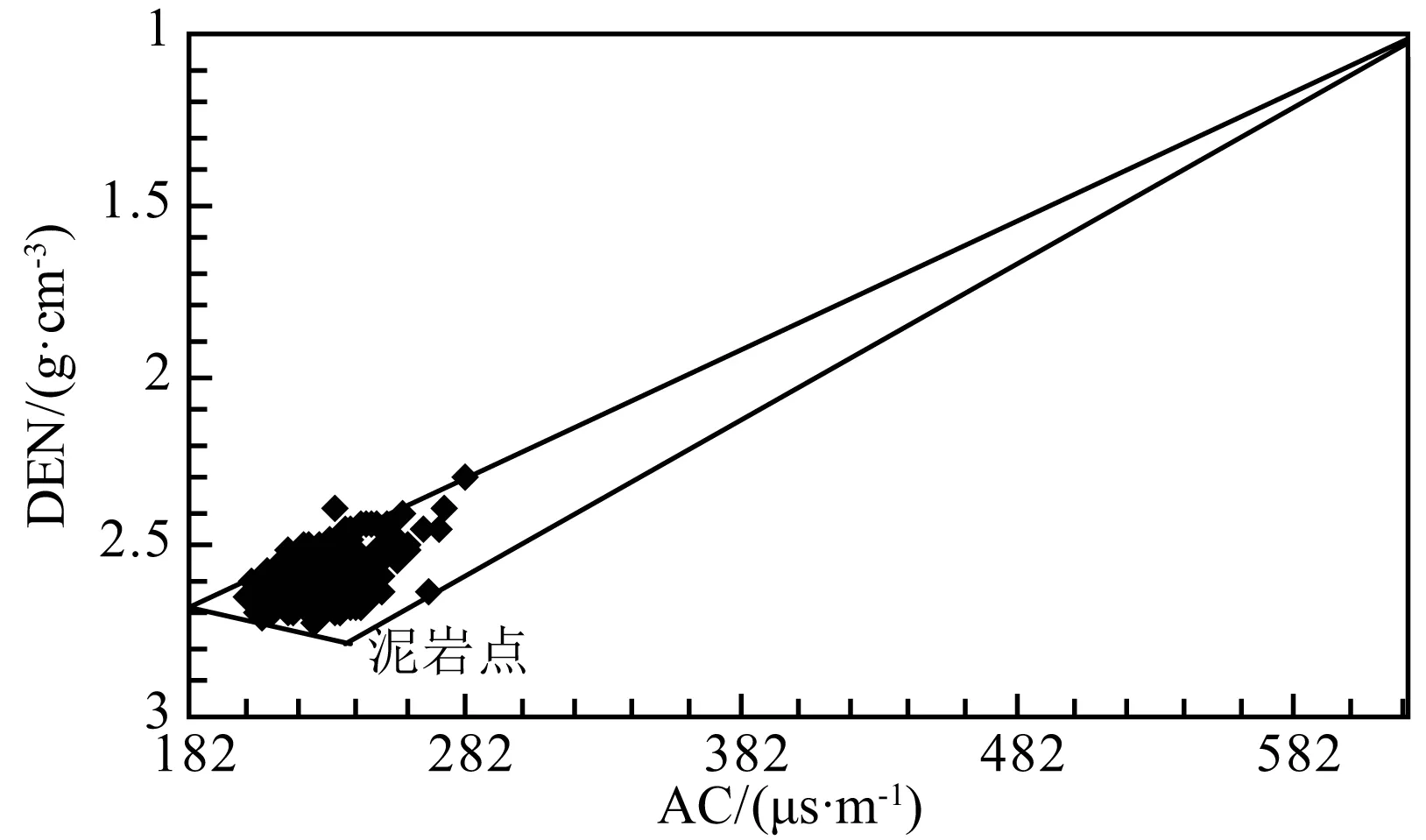
图7 声波-密度交会图
通过绘制研究区内某井段中子-密度交会图(图6)、声波-密度交会图(图7)确定泥质对密度、中子及声波测井的响应值(ρcl、φNcl、Δtcl)分别为2.75 g·cm-3、37%、240 μs·m-1.根据主要矿物测井特征表(雍世和,1995)和主要火成岩测井响应特征(Serra,1986)确定孔隙流体及各骨架组分的测井特征值如表1.

表1 孔隙流体及各骨架组分的测井响应特征值
3.5目标函数的约束条件
在寻找最优解的过程中,为了得到合理的解释结果,应该对未知量x进行限制.一般说,多组分解释模型的约束条件包括数学物理约束、地区地质约束和连续性约束(雍世和,1995).本文主要目的是进行BFA-CM混合算法研究,为提高运算效率,文中只考虑数学物理约束条件,如式(4)所示.
(4)
4实际资料处理与检验
分别利用遗传算法(GA)、粒子群算法(PSO)、BFA算法及BFA-CM混合算法求解最优化测井解释方法中的未知储层参数,其绝对误差见表2.由表2可以发现,BFA-CM混合算法计算结果的准确性明显高于其他算法.GA和PSO算法都是以高等生物为模拟对象,通过“生成+检验”的方式寻求最优解.而BFA算法则以微生物为模拟对象,通过细菌群体的竞争与协作来实现优化.与GA算法相比,BFA算法增加了方向信息,提高了搜索效率;与PSO算法相比,BFA算法引进了迁移算子,可以避免算法陷入局部极值点.图8为BFA算法求解最优化测井解释方法未知储层参数的结果图.由图8可以发现,单独运用BFA算法求解得到的各储层参数曲线的毛刺较多,这是由于BFA算法后期收敛速度变慢所造成的.图9为BFA-CM混合算法求解最优化测井解释方法未知储层参数的结果图.BFA-CM混合算法克服了BFA算法的缺点,提高了求解后期算法的收敛速度,计算结果与岩心及薄片分析资料吻合度更高,孔隙度及各组分含量曲线也更加稳定.
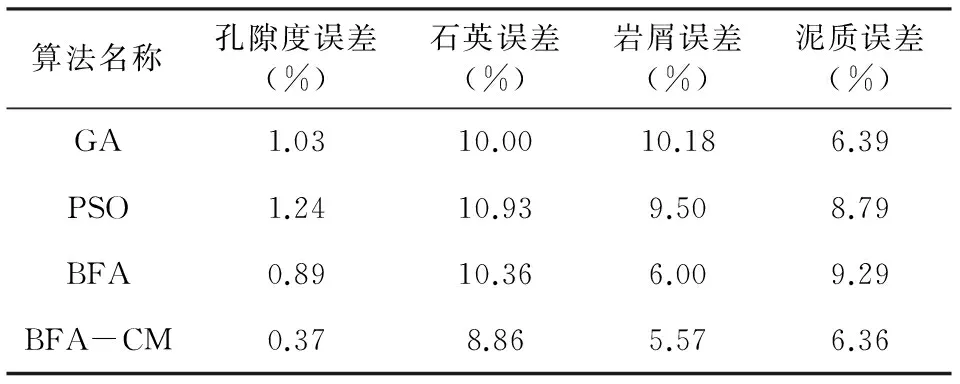
表2 各算法绝对误差统计表
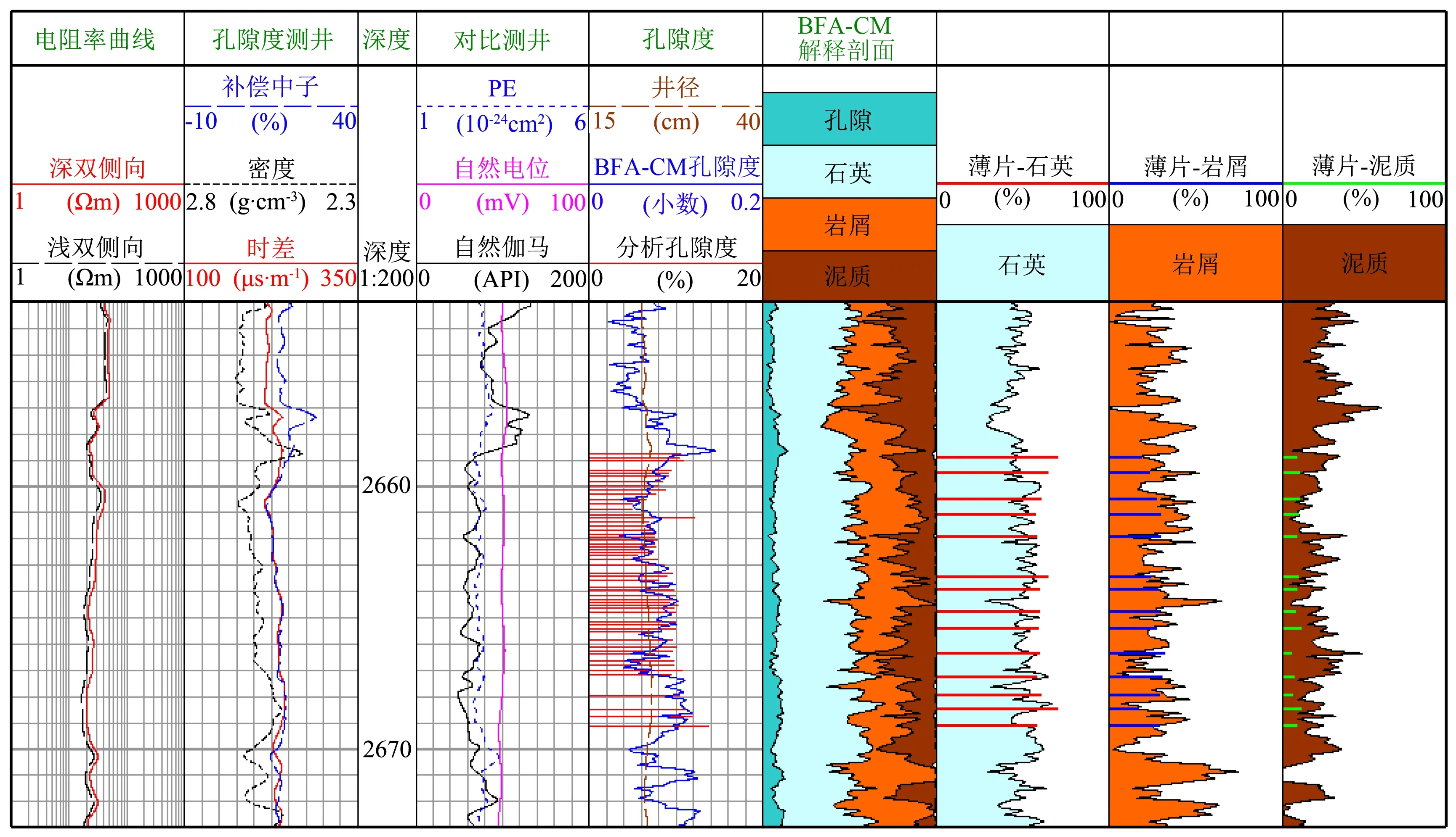
图8 xx井BFA最优化测井解释方法处理结果图
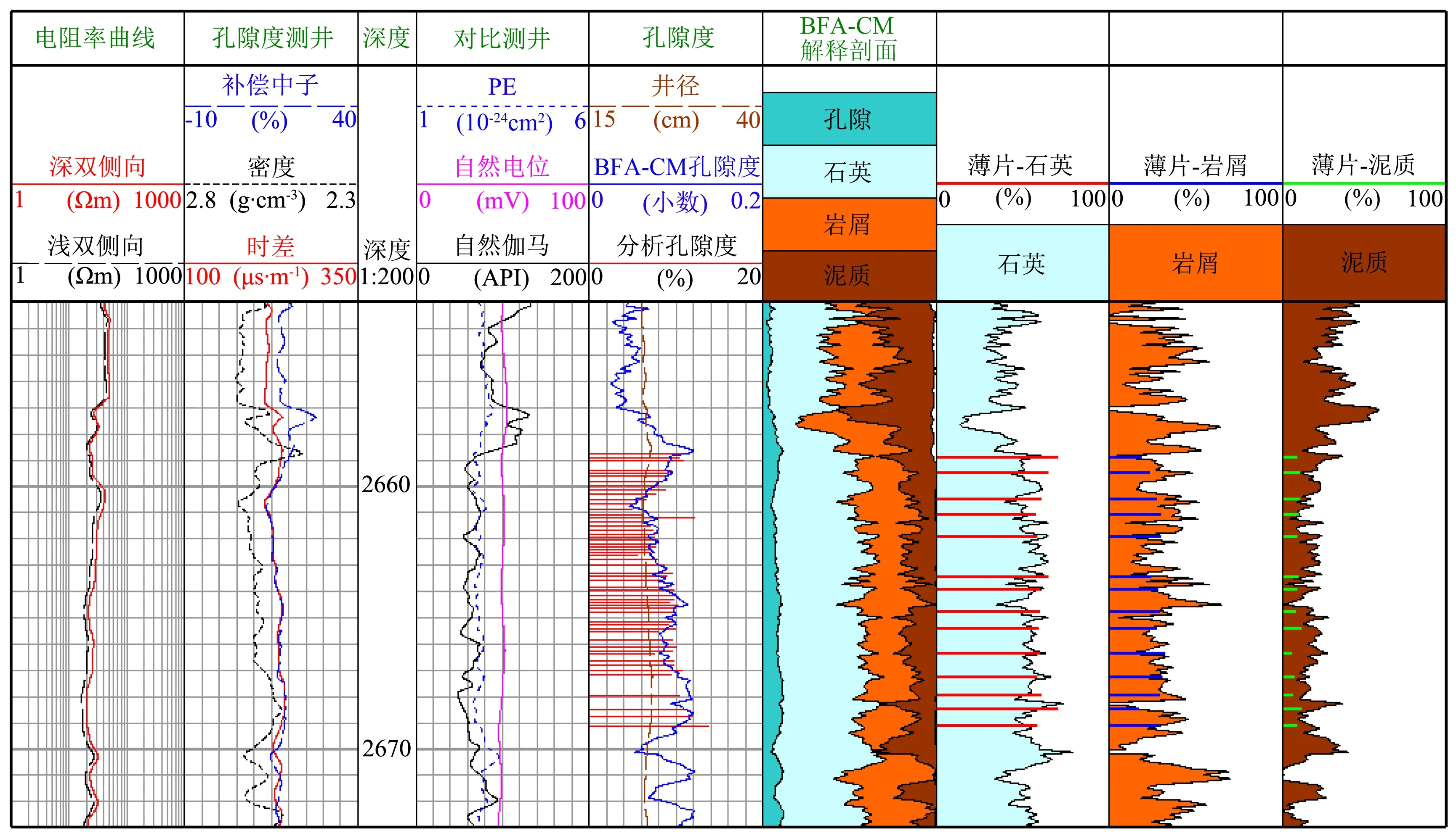
图9 xx井BFA-CM最优化测井解释方法处理结果图
图10为xx井BFA-CM最优化测井解释处理检验图,图中F为最优化测井解释目标函数值,单位为10-8;AC0、CNL0、DEN0分别为声波、中子、密度理论测井值曲线;AC 、CNL、DEN分别为声波、中子、密度实际测井值曲线;右侧三道内黑色虚线分别为理论测井曲线AC0、CNL0、DEN0的置信区间.图10中最优化测井解释目标函数值F≈0(3×10-9~3.797×10-6),说明最优化计算结果具有较高质量,所用的解释模型、解释参数合理.AC0、CNL0、DEN0均落在置信区间内,说明不存在系统偏差影响,优化计算结果合理可信.
5结论
细菌觅食算法(BFA)是一种新兴的智能优化算法,不需要求解目标函数的导数且具有较强的全局搜索能力.但该算法在求解后期收敛速度变慢,寻优效率变低.本文将BFA算法应用于最优化测井解释方法中,并将其与CM算法相结合构成BFA-CM混合算法以提高求解的准确率和效率.实践证明,BFA-CM混合算法可以既准确又高效地求解得到最优化测井解释方法的最优解,可推广于生产实践中.
References
Chu Y, Shao Z B, Mi H, et al. 2008. An application of bacterial foraging algorithm in image compression.JournalofShenzhenUniversityScienceandEngineering(Science&Engineering) (in Chinese), 25(2): 153-157.
Duan Y N, Pan B Z, Han X. 2012. Multi-component model and the optimize logging interpretation of glutenite reservoirs.WorldWellLoggingTechnology(in Chinese), 33(6): 20-23.
Gong S Y, Dou L M, Ma X P, et al. 2012. Study on the construction and solution technique of anisotropic velocity model in the location of coal mine tremor.ChineseJ.Geophys. (in Chinese), 55(5): 1757-1763, doi: 10.6038/j.issn.0001-5733.2012.05.033.
Han X. 2012. Research on glutenite reservoirs with GA-CM hybrid optimization log interpretation method in Lishu Fault Depression [master′s thesis] (in Chinese). Changchun: Jilin University.
Kim D H, Cho J H. 2005. Adaptive tuning of PID controller for multivariable system using bacterial foraging based optimization.∥ Advances in Web Intelligence. Berlin Heidelberg: Springer, 231-235. Kim D H, Cho J H. 2006. A biologically inspired intelligent PID controller tuning for AVR systems.InternationalJournalofControl,Automation,andSystems, 4(5): 624-636.
Liu X L. 2011. Modification and application of bacterial foraging optimization algorithm [Ph. D. thesis] (in Chinese). Guangzhou: South China University of Technology.
Luo M Q, Zhu G T, Liu H, et al. 2003. A hybrid method of matrix inversion suited for 3D implicit prestack depth migration.ChineseJ.Geophys. (in Chinese), 46(5): 684-689.
Passino K M. 2002. Biomimicry of bacterial foraging for distributed optimization and control.IEEEControlSystemsMagazine, 22(3): 52-67.
Serra O. 1986. Fundamentals of Well-log Interpretation: The Acquisition of Logging Data. Developments in Petroleum Science. Amsterdam: Elsevier Science. Tan M J, Zou Y L. 2012. A hybrid inversion method of (T2, D) 2D NMR logging and observation parameters effects.ChineseJ.Geophys. (in Chinese), 55(2): 683-692, doi: 10.3969/j.issn.0001-5733.2012.02.032.
Tian Y Y, Xia H Q. 2006. Optimization log interpretation based on multi-mineral model analysis.JournalofSouthwestPetroleumInstitute(in Chinese), 28(4): 8-11.
Tripathy M, Mishra S, Lai L L, et al. 2006. Transmission loss reduction based on FACTS and bacteria foraging algorithm. ∥ Parallel Problem Solving from Nature-PPSN IX. Berlin Heidelberg: Springer, 222-231.
Wang C P. 2013. Quantitative evaluation of reservoir parameters and movable fluid in tight gas sandstone [master′s thesis] (in Chinese). Changchun: Jilin University.
Yong S H. 1995. Optimization Log Interpretation Method (in Chinese). Dongying: Petroleum University Press.
You M L, Lei X J. 2013. An improved bacterial foraging algorithm for the traveling salesman problem.JournalofGuangxiUniversity(NaturalScienceEdition) (in Chinese), 38(6): 1436-1443.
Zhang C. 2013. Improved bacterial foraging algorithm and its application to the structural optimal design [master′s thesis] (in Chinese). Guangzhou: Guangdong University of Technology.
Zhang N. 2007. Study on job-shop scheduling problems based on bacteria foraging optimization algorithm [master′s thesis] (in Chinese). Changchun: Jilin University.
Zhang X H, Zhang J F, Zeng J J. 2003. An improved algorithm of complex method in optimization.JournalofSichuanUniversityofScienceandTechnology(in Chinese), 22(2): 21-23.
附中文参考文献
储颖, 邵子博, 糜华等. 2008. 细菌觅食算法在图像压缩中的应用. 深圳大学学报(理工版), 25(2): 153-157.
段亚男, 潘保芝, 韩雪. 2012. 砂砾岩储层的多组分模型及最优化测井解释. 国外测井技术, 33(6): 20-23.
巩思园, 窦林名, 马小平等. 2012. 煤矿矿震定位中异向波速模型的构建与求解. 地球物理学报, 55(5): 1757-1763, doi: 10.6038/j.issn.0001-5733.2012.05.033.
韩雪. 2012. 梨树断陷砂砾岩储层GA-CM混合最优化测井解释方法研究[硕士论文]. 长春: 吉林大学.
刘小龙. 2011. 细菌觅食优化算法的改进及应用[博士论文]. 广州: 华南理工大学.
罗明秋, 朱国同, 刘洪等. 2003. 适用于三维隐式叠前深度偏移中矩阵求逆的混合算法. 地球物理学报, 46(5): 684-689.
谭茂金, 邹友龙. 2012. (T2, D)二维核磁共振测井混合反演方法与参数影响分析. 地球物理学报, 55(2): 683-692, doi: 10.3969/j.issn.0001-5733.2012.02.032.
田云英, 夏宏泉. 2006. 基于多矿物模型分析的最优化测井解释. 西南石油学院学报, 28(4): 8-11.
王翠平. 2013. 致密含气砂岩储层参数及可动流体的定量评价[硕士论文]. 长春: 吉林大学.
雍世和. 1995. 最优化测井解释. 东营: 石油大学出版社.
尤梦丽, 雷秀娟. 2013. 改进的细菌觅食算法求解TSP问题. 广西大学学报(自然科学版), 38(6): 1436-1443.
张璨. 2013. 改进的细菌觅食算法及其在结构优化设计中的应用[硕士论文]. 广州: 广东工业大学.
张娜. 2007. 细菌觅食优化算法求解车间调度问题的研究[硕士论文]. 长春: 吉林大学.
张晓洪, 张钧富, 曾钰钰. 2003. 一种复合形优化方法的改进算法. 四川工业学院学报, 22(2): 21-23.
(本文编辑何燕)
基金项目国家科技重大专项《大型油气田及煤层气开发》“鄂尔多斯盆地大型低渗透岩性地层油气藏开发示范工程”(2011ZX05044)与国家自然科学基金项目“松辽盆地深层火成岩CO2气藏岩石物理参数研究”(41174096)联合资助.
作者简介潘保芝,女,1962年生,2002年于吉林大学地球探测科学与技术学院获博士学位,主要研究方向为地球物理测井. *通讯作者段亚男,女,1989年生,主要从事最优化测井解释方法方面的研究工作.E-mail:dynjlu@163.com
doi:10.6038/cjg20160133 中图分类号P631
收稿日期2014-11-30,2015-12-14收修定稿
BFA-CM optimization log interpretation method
PAN Bao-Zhi1, DUAN Ya-Nan1,2*, ZHANG Hai-Tao3, YANG Xiao-Ming3, HAN Xue4
1CollegeofEarthExplorationScienceandTechnology,JilinUniversity,Changchun130061,China2MaterialTestingExplorationInstituteofLiaoningProvince,Shenyang110121,China3ExplorationandDevelopmentInstituteofChangqingOilfield,PetroChina,Xi′an710021,China4FirstBranchoftheLoggingCompany,ShengliPetroleumEngineeringCo.Ltd.,ShandongDongying257200,China
AbstractIt is difficult to calculate reservoir parameters of the tight sand reservoirs by conventional interpretation methods, because their lithology is complex and the pore structure is variable. The optimization log interpretation method can take full advantages of log data and geological information, so it is an effective method to evaluate tight sand reservoirs. First, in order to calculate reservoir parameters of the tight sand reservoirs, an appropriate interpretation model need to be established according to reservoir characteristics. Then, the interpretation parameters are chosen and the specific form of the objective function is determined. Next, an optimization algorithm is adopted to search for the optimal solution. The bacterial foraging algorithm (BFA) is a newly developed algorithm which has a strong global search capability. It simulates the behavior of the colon bacillus, which swim with flagella for food in the human gut, but it converges slowly in the latter part of the optimization. So it is combined with complex algorithm (CM) for constituting BFA-CM hybrid algorithm to improve the precision and efficiency of searching. Unknown reservoir parameters of the optimization log interpretation method are respectively determined by the genetic algorithm (GA), particle swarm optimization (PSO), BFA algorithm and BFA-CM hybrid algorithm. The calculation results show that compared with GA and PSO, the errors of the porosity and the component content calculated by BFA are minima, but the calculation result curves are jumpy. By combining BFA algorithm with CM algorithm for constituting the BFA-CM hybrid algorithm to calculate reservoir parameters, the accuracy can be improved and the curves become more stable. The results of the BFA-CM optimization log interpretation method have been verified that the objective function value F≈0, and sonic, neutron, density log theoretical value curves (AC0, CNL0, DEN0) fall within the confidence interval, indicating that the system deviation influence does not exist and the optimization results are reasonable and credible. Compared to other algorithms, the BFA-CM hybrid algorithm shows unique advantages in the process of calculating the unknown parameters with the optimization log interpretation method. Its calculation results are of high accuracy and stability, and the efficiency has also been improved. Experimental results show that the BFA-CM optimization logging interpretation method can accurately calculate tight sandstone reservoir parameters, and can be applied to production practice.
KeywordsBacterial foraging algorithm; Optimization; Log interpretation; Complex algorithm; Hybrid algorithm
潘保芝, 段亚男, 张海涛等. 2016. BFA-CM最优化测井解释方法.地球物理学报,59(1):391-398,doi:10.6038/cjg20160133.
Pan B Z, Duan Y N, Zhang H T, et al. 2016. BFA-CM optimization log interpretation method.ChineseJ.Geophys. (in Chinese),59(1):391-398,doi:10.6038/cjg20160133.

