大麻坪橄榄石冲击波实验研究与高压态物态方程参数的确定

陈祖安， 袁贤昊， 黄晓葛， 刘福生， 地力夏提， 白武明

1 中国科学院地质与地球物理研究所中国科学院地球与行星物理重点实验室， 北京　100029 2 西南交通大学高温高压物理研究所, 成都　610031



大麻坪橄榄石冲击波实验研究与高压态物态方程参数的确定

陈祖安1， 袁贤昊2， 黄晓葛1， 刘福生2， 地力夏提1， 白武明1

1 中国科学院地质与地球物理研究所中国科学院地球与行星物理重点实验室， 北京100029 2 西南交通大学高温高压物理研究所, 成都610031

摘要利用冲击波进行的动高压实验对研究超高压下的物质性质也是十分有效的.本文报告了对大麻坪采集的橄榄石进行压力在10～45 GPa范围的冲击波动高压实验结果.结合前人等温冷压实验结果，确定了实验过程的温度，对于冲击波实验压力从10 GPa变化到30 GPa时，温度在摄氏几十度到摄氏800多度之间.测量了岩石超高压下密度变化，在3.627～4.009 g·cm-3之间.通过回收实验和确定的温度，表明小于30 GPa压力实验条件下，没有发生相变过程.同时也确定了状态方程的参数.最后，指出了实验结果在上地幔地球内部物质运动过程的含义，即冷板块中的亚临界橄榄岩可以存在地幔转换带中.

关键词动高压； 大麻坪橄榄石； 状态方程； 密度

1引言

橄榄石是上地幔最主要的矿物，它由平均大约90% mol Mg2SiO4和10% mol Fe2SiO4组成.橄榄石的状态方程(EOS)的确定非常重要，因为通过与观察的地震数据它可被使用来约束上地幔的组分和矿物模型，帮助理解上地幔的动力学.至今.许多含铁橄榄石弹性实验研究已经进行，不同研究者使用不同的方法，如静态压缩(Kumazawa and Anderson, 1969; Isaak, 1992; Zaug et al., 1993; Meng et al., 1993; Guyot et al.,1996; Abramson et al., 1997; Zha et al., 1998; Li et al.,2004; Liu et al.,2005；Liu and Li, 2006).然而，实验条件局限在室温和高压下(Zaug et al, 1993; Abramson et al., 1997; Zha et al., 1998)，或者常压和高温下(Isaak, 1992).基于原位高P-T测量的热状态方程研究其压力也小于8 GPa(Meng et al., 1993; Guyot et al.,1996; Liu et al.,2005；Liu and Li, 2006).通过冲击波压缩实验，一些研究者(McQueen et al.,1968; Van Thiel et al., 1967； Birch et al.,1966)已经得到压力达到100 GPa下的橄榄石P-V曲线.但是，热状态方程数据对于不同研究变化非常大.

橄榄石可以在地球深部410 km处转变成wadsleyite，在深部520 km处 转变成ringwoodite.地震观测证据表明俯冲带可能插入地幔转换带410～660 km之间.俯冲板片同周围环境相比处于相对低压高温状态.板片中的橄榄石如何拖进地幔转换带？

利用冲击波进行的动高压实验对研究超高压下的物质性质也是十分有效的.自20世纪60年代以来，关于金属和矿物的冲击波实验已有大量研究成果发表.这些研究包括了对高压下物质密度、声速变化、相变、熔化、输运和物质状态方程等性质的探索.

本文对大麻坪采集的热压后橄榄石0.1的Fe/(Mg+Fe) 样品进行压力在10～45 GPa范围的冲击波动高压实验，对岩石超高压下密度变化、相变过程和状态方程进行研究，并探讨了该项研究对于含有橄榄岩俯冲板块存在地幔转换带区域的地球物理含义.

2实验方法

实验所用的橄榄石来自河北省张家口的大麻坪的二辉橄榄岩，它的XRD谱如图1所示.首先通过人工手动挑选，然后研磨成小于63目的粉末，再装入铁皮制成的圆柱体中，最后在130 MPa和1400 K下真空热压成型.实验前，样品被切割、抛光成圆片状，并焊接光纤，组装后放入实验腔体，如图2所示.实验时，化学炸药爆炸推动飞片高速运动，当撞击样品后，在样品中产生一个以速度D向前传播的冲击波，受冲击波压缩后物质以速度u运动.在无相变情况下，实验和理论都证明，D和u可用下述关系式描述(谭华, 2007)：

(1)

式中，c0为零压体积声速，λ为依赖于样品材料性质的常数.根据质量守恒、动量守恒及能量守恒定律可得到压强p和密度ρ：

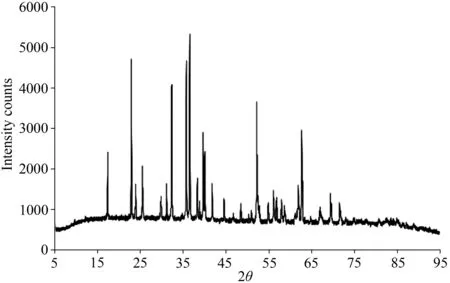
图1　样品XRD测试分析

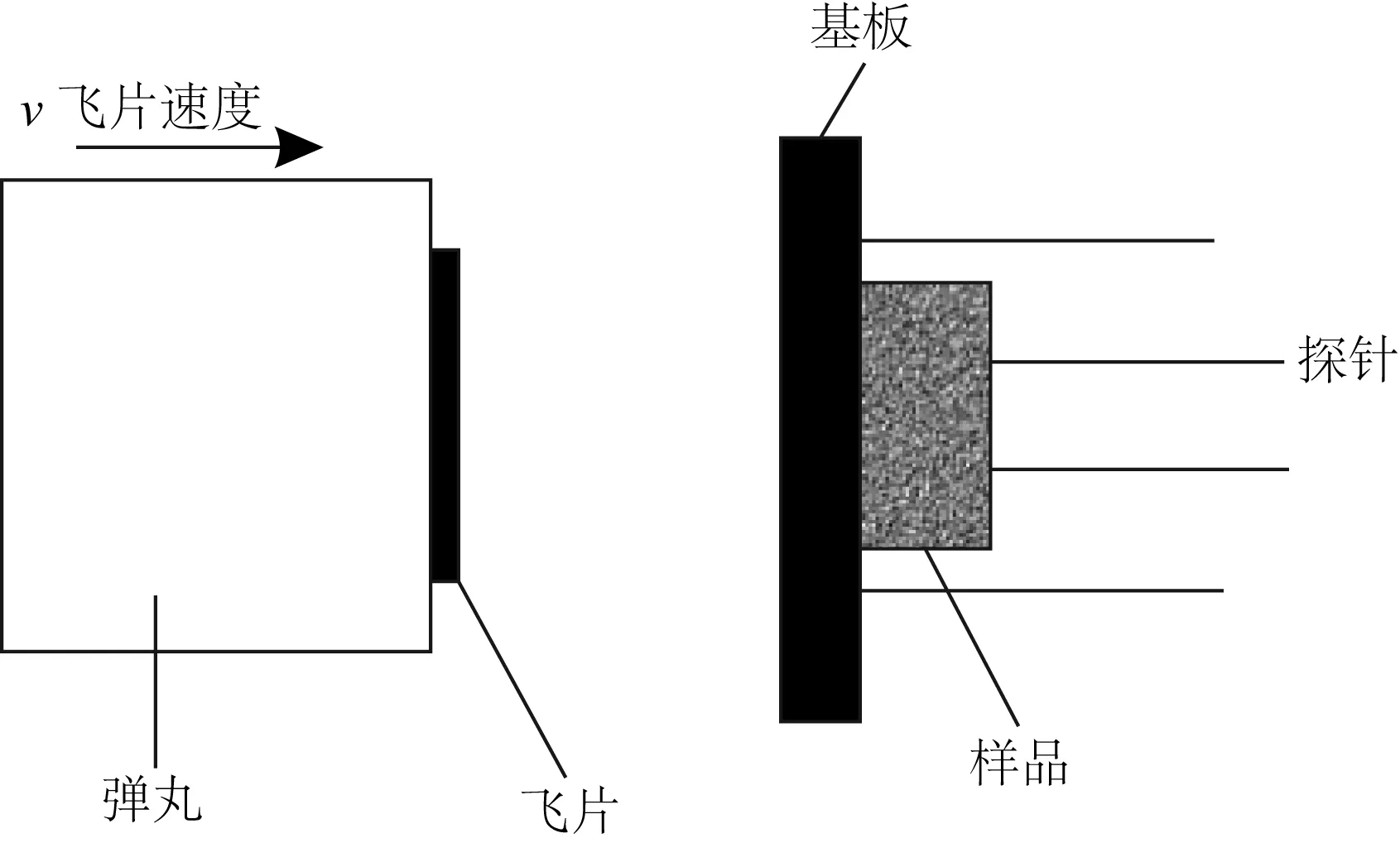
图2　实验装置示意图

p=ρ0Du,

(2)

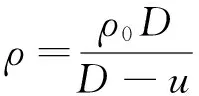
(3)

其中，ρ0为初始密度.

3实验结果

在10～45 GPa压力范围内进行了10发冲击压缩实验，结果列于表1.观察实验数据以及回收实验结果，判定我们实验结果没有发生相变.线性拟合冲击波速度D和粒子速度u的关系可得c0和λ为3.56和2.57，如图3所示.图4表明了动高压条件下橄榄岩密度和压力的关系.

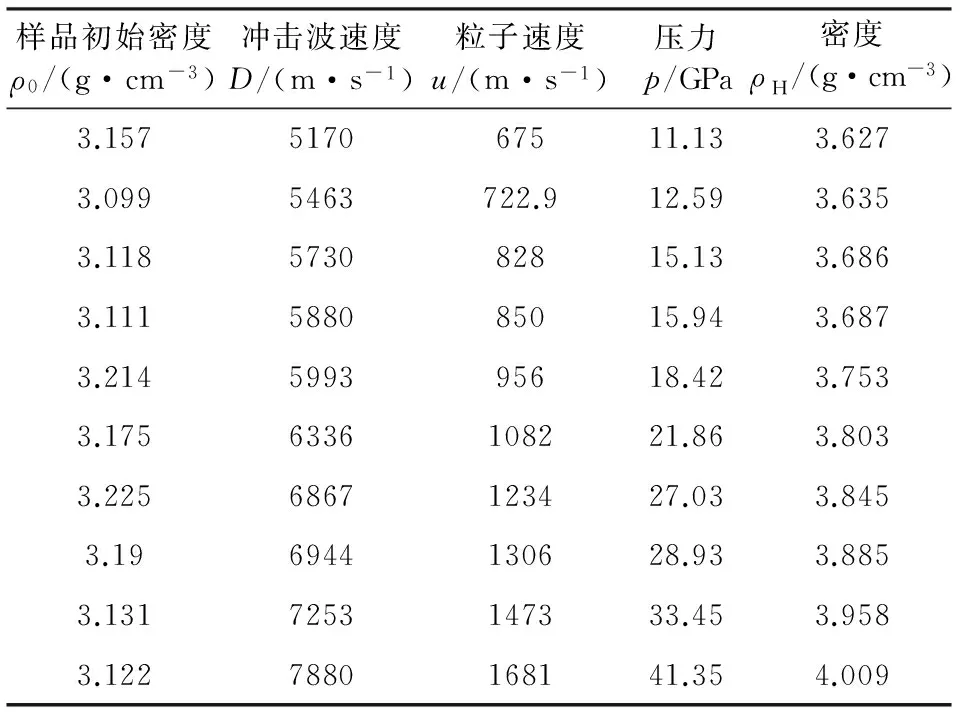
表1　橄榄岩冲击压缩实验数据

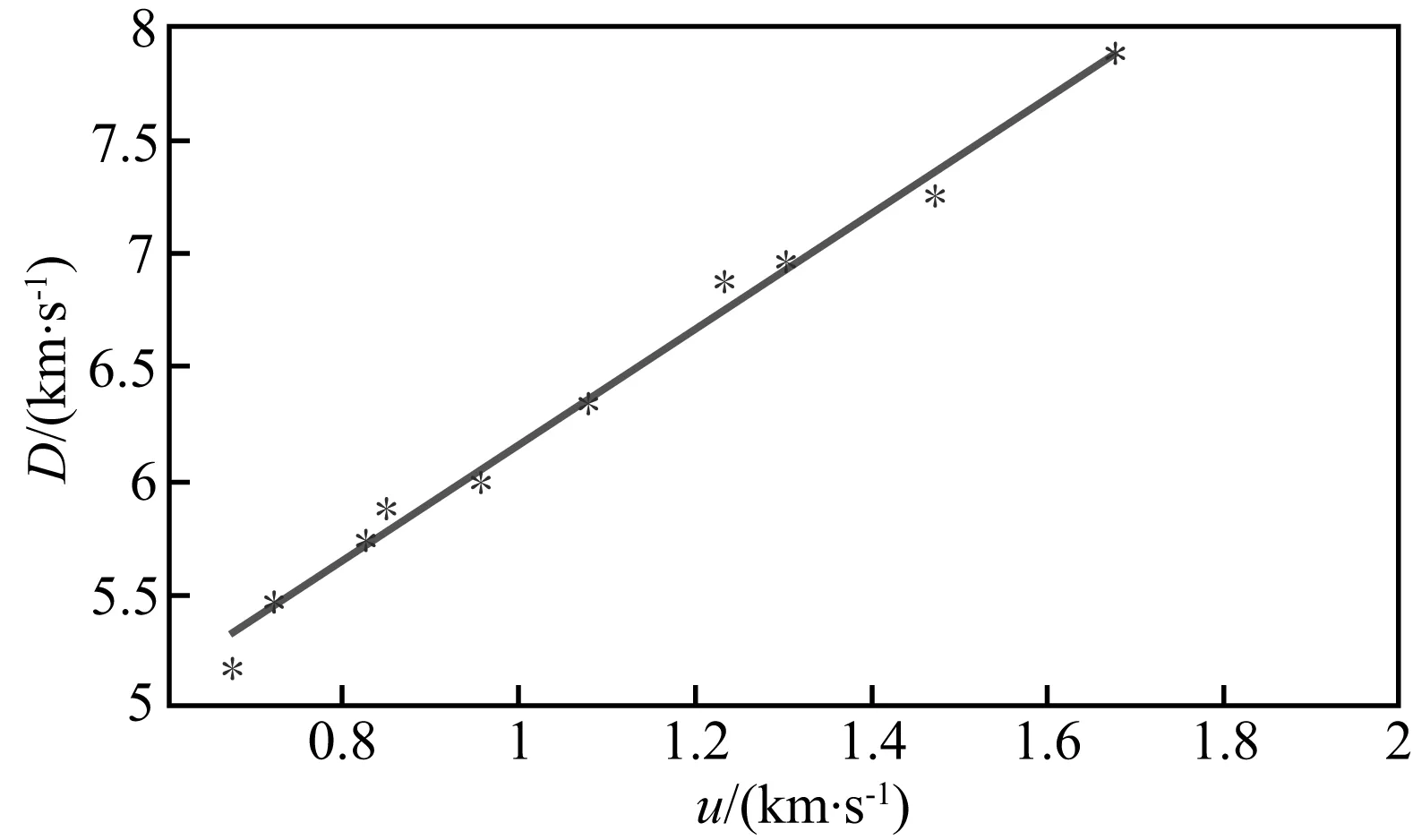
图3　冲击波速度与粒子速度的关系

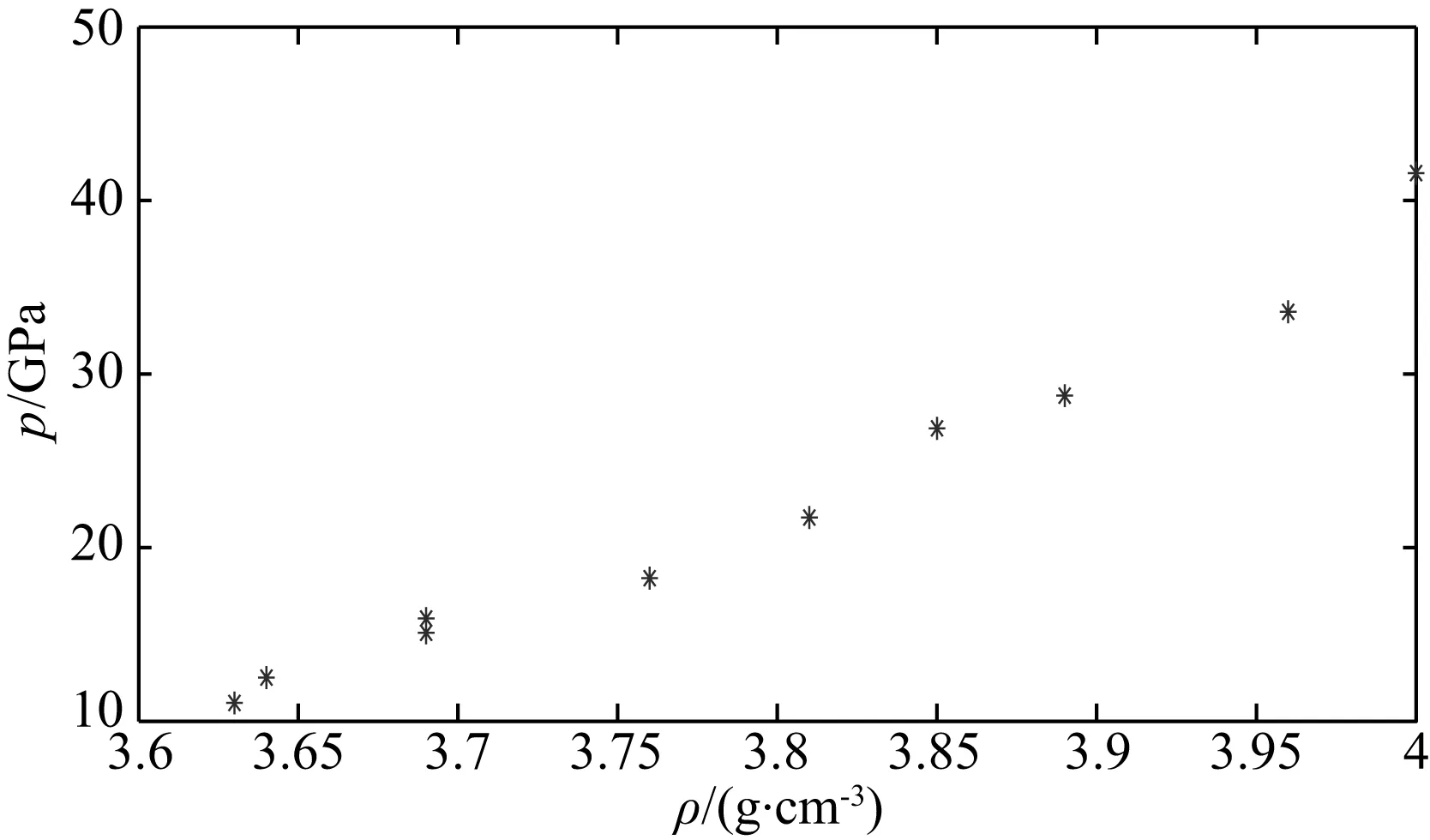
图4　橄榄岩动高压实验条件下压力与密度的关系

4物态方程参数确定

在固体和液体系统的物态方程研究中，从系统的薛定谔方程出发，通过绝热近似或静态近似，系统的物态方程分成由电子及点阵两个子系统的贡献相加得到，并进一步把这两部分贡献分成零温部分和非零温部分.零温部分能量和压力分别称为冷能Ec和冷压pc，非零温贡献部分分别称为热能ET和热压pT.因此，总能量可分为热能和冷压能：

(4)

这里代表EH总能量.对于冲击波压缩过程，总能量为Rankin-Hugoniot能量关系式：

(5)

冷能即常温下与压力有关的能量为

(6)

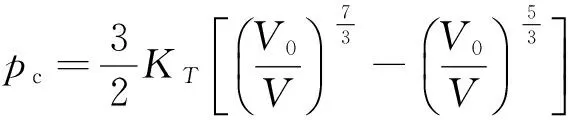
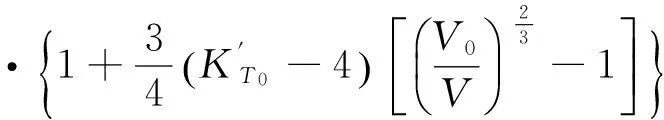
(7)

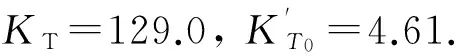
对固体及液体系统, 在小于几百吉帕的压力范围内，在系统的物态方程中，一般可略去电子项贡献，并用以下形式的Gruneisen物态方程描述(经福谦,1999):

(8)

(9)

式中，p为压力，V为比容(密度ρ的倒数)，T为温度，γ是Gruneisen系数.由(8,9)式可见, 如果知道pc(或Ec)和总能量EH,γ(V)就可以被确定，从而也就确定了材料的物态方程.

设Gruneisen系数随比容的变化满足n幂次关系

(10)

由我们关于橄榄岩实验结果和前人冷能和冷压结果(见方程(6)和(7))，得到γ依赖V的数据，拟合上面关系式，可得n=13.5,γ0=227.39.

5实验温度的确定

结合前人关于橄榄岩等温冷压的实验结果，根据热力学能量关系，可以确定实验过程的温度.

热能即等压过程与温度有关的能量为

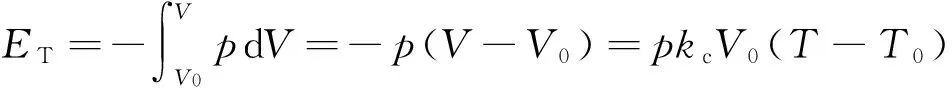
(11)

其中，kc为热膨胀系数.于是

(12)

结合方程(4)— (7)，并取kc=2.73×10-5K-1(Liu and Li, 2006), 由我们的动高压实验结果和前人室温静态高压结果，可确定我们实验对应各个压力下的温度，结果如图5所示.由图可发现我们的冲击波实验压力从10 GPa到30 GPa，温度从摄氏几十度到摄氏800多度之间.这也间接地表明我们的实验在此过程中没有发生相变.

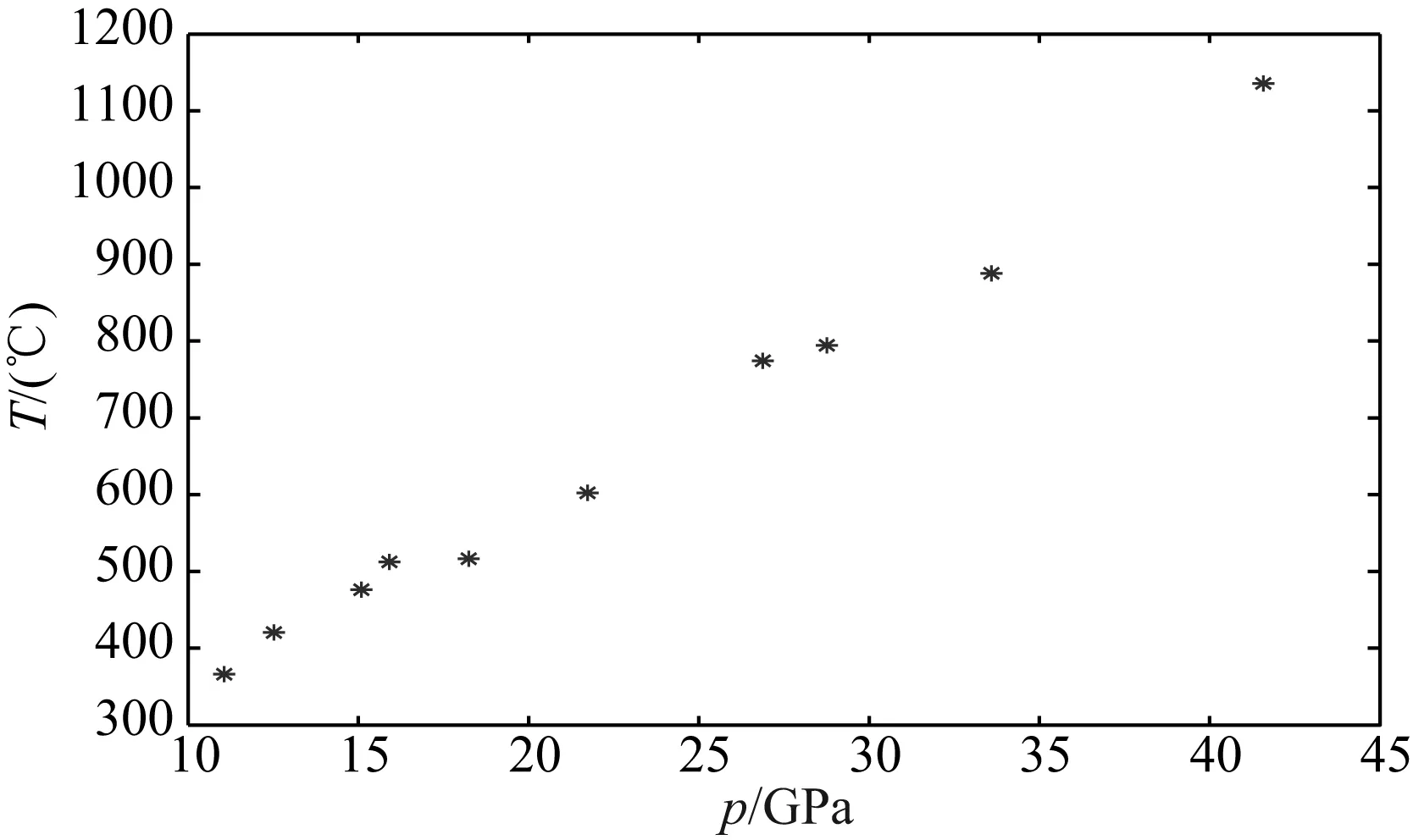
图5　冲击波实验对应相应压力下温度的确定

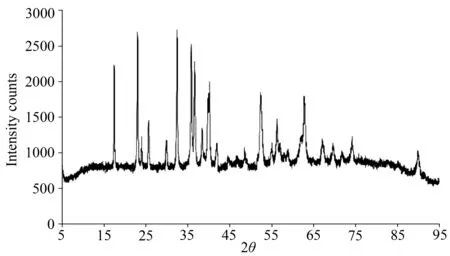
图6　橄榄岩回收实验后的XRD谱图

6实验样品相分析

从冲击波速度和粒子速度关系曲线(如图3所示)的特征，及我们所做的回收试验(压力为28 GPa)回收样品的化学检测结果(图6)都表明，在我们的实验条件下，或严格的说压力小于30 GPa时，没有发生相变.这从第5节确定的温度结果也可推断出.即使在压力和温度都达到相变条件的情况下，对于冲击波动高压实验样品也不一定就发生相变.因为，动高压实验时间极短，相变可能来不及发生，而处于亚稳定过程.

7讨论

由于相变过程除了要求一定的温压条件，适当的时间也是需要的.而我们的动高压实验，样品受压时间极短，温度也没有达到很高，因而在压力28.76 GPa以下，我们的样品在冲击波压缩下没有发生相变，可能处在亚稳态相.

板块中亚稳态橄榄岩的存在对于板块俯冲和深部地震起源有着重要的含义.以前亚稳态的橄榄岩在压力高于10 GPa的密度还没有直接测量.使用橄榄岩的热弹性参数(Liu and Li, 2006), 构造出在温度为873K和压力从0到35 GPa压力密度曲线.它与我们动高压结果较好的吻合.地球深部410 km(14 GPa)和660 km(24 GPa)处，亚稳态橄榄岩密度是3.67 g·cm-3和3.82 g·cm-3, 在410 km下,这个密度高于PREM和AK135 模型，这也说明冷板块俯冲更加容易.作为西太平洋俯冲区的例子，如果板块的俯冲速率是8～12 cm·a-1，地热梯度是0.6 K·km-1. 在300 km处的温度设为800 K(Tetalaff and Schmeling, 2009), 俯冲角设为30°.板块需要大约7～10 Ma 俯冲到410 km 深度.假设板块厚度d是80 km，热扩散系数是κ是10-6m2·s-1.由公式t=d2/4κ, 可以估计需要大约12.6 Ma加热板块.上述结果表明冷板块中的亚临界橄榄岩可以存在地幔转换带中.

8结论

1) 本文叙述了我们对大麻坪橄榄石进行的十发冲击波动高压压力在10～45 GPa范围内的实验结果，得到了绝热压缩雨贡纽曲线.利用前人的冷压方程确定了实验过程的温度.实验结果表明实验过程中没有发生相变.

2) 利用绝热压缩曲线和冷压曲线可确定材料物态方程.由冲击绝热数据和前人冷压方程，计算得到了大麻坪橄榄石的格临爱森系数与比容幂次关系的参数n=13.5,γ0=227.35.由此确定了大麻坪橄榄岩Gruneisen物态方程.

3) 实验结果表明，冷板块中的亚临界橄榄岩可以存在地幔转换带中.

致谢实验是在西南交大高压物理实验室进行的. 对张明建和薛学东二位老师在实验过程中的帮助表示衷心感谢.感谢审稿人提出的建议.

References

Abramson E H, Brown J M, Slutsky L J, et al. 1997. The elastic constants of San Carlos olivine to 17 GPa.JournalofGeophysicalResearch, 102(B6): 12253-12264.Birch F. 1966. “Compressibility; Elastic Constants” in Handbook of Physical Constants, revised edition, Clark, Jr, ed. New York: The Geological Society of America, Inc., 153-159.

Guyot F, Wang Y B, Gillet P, et al. 1996. Quasi-harmonic computations of thermodynamic parameters of olivines at high-pressure and high-temperature. A comparison with experiment data.PhysicsoftheEarthandPlanetaryInteriors, 98(1-2): 17-29.Isaak D G. 1992. High-temperature elasticity of iron-bearing olivines.JournalofGeophysicalResearch, 97(B2): 1871-1885.Jing F Q. 1999. Experimental Equation of State (Second Edition) (in Chinese). Beijing: Science Press. Kumazawa M, Anderson O L. 1969. Elastic moduli, pressure derivatives, and temperature derivatives of single-crystal olivine and single-crystal forsterite.JournalofGeophysicalofResearch, 74(25): 5961-5972. Li B S, Kung J, Liebermann R C. 2004. Modern techniques in measuring elasticity of Earth materials at high pressure and high temperature using ultrasonic interferometry in conjunction with synchrotronX-radiation in multi-anvil apparatus.PhysicsoftheEarthandPlanetaryInteriors, 143-144: 559-574.Liu W, Li B S. 2006. Thermal equation of state of (Mg0.9Fe0.1)2SiO4olivine.PhysicsoftheEarthandPlanetaryInteriors, 157(3-4): 188-195.Liu W, Kung J, Li B. 2005. Elasticity of San Carlos olivine to 8 GPa and 1073 K.Geophys.Res.Lett., 32: L16301.

McQueen R G. 1968. The equation of state of mixtures, Allys, and compounds in seismic coupling. Simmons ed. Proceedings of a meeting sponsored by the adfnaced research projects agency at Stanford Research Institute, Menlo Park , California. 15-16.

Meng Y, Weidner D J, Gwanmesia D, et al. 1993. In situ highP-TXray diffraction studies on three polymorphs (α,β,γ) of Mg2SiO.JournalofGeophysicalResearch, 98(B12): 22199-22207.

Tan H. 2007. Introduction to Experimental Shock-Wave Physics (in Chinese). Beijing: National Defense Industry Press. Tetzlaff M, Schmeling H. 2009. Time-dependent interaction between subduction dynamics and phase transition kinetics.Geophys.J.Int., 178(2): 826-844.Van Thiel M, Kusubov A S, Mitchell A C. 1967. compendium of shock wave data. Lawrence Radiation Laboratory(Livermore) report UCRL-50108.

Zha C S, Duffy T S, Downs R T, et al. 1998. Brillouin scattering andX-ray diffraction of San Carlos olivine: direct pressure determination to 32 GPa.EarthandPlanetaryScienceLetters, 159(1-2): 25-33.

Zaug J, Abramson E H, Borwn J M, et al. 1993. Sound velocities in olivine at Earth mantle pressures.Science, 260: 1487-1489.

附中文参考文献

经福谦. 1999. 实验物态方程导引(第二版). 北京: 科学出版社.

谭华. 2007. 实验冲击波物理导引. 北京: 国防工业出版社.

(本文编辑汪海英)

基金项目国家自然科学基金项目(41174073、41174074)和中国科学院创新项目(KZCX-EW-118)资助.

作者简介陈祖安，男，1963年生，博士，副研究员.主要从事地球动力学研究. E-mail:zachen@mail.iggcas.ac.cn

doi:10.6038/cjg20160112 中图分类号P312

收稿日期2014-12-02，2015-10-23收修定稿

A shock wave experimental study on Damaping olivine and estimation of its parameters for equation of state

CHEN Zu-An1, YUAN Xian-Hao2, HUANG Xiao-Ge1, LIU Fu-Sheng2, DILI Xiati1, BAI Wu-Ming1

1KeyLaboratoryofEarthandPlanetaryPhysics,InstituteofGeologyandGeophysics,ChineseAcademyofSciences,Beijing100029,China2InstituteofHighTemperatureandHighPressurePhysics,KeyLaboratoryofAdvancedTechnologiesofMaterials,MinistryofEducationofChina,SouthwestJiaotongUniversity,Chengdu610031,China

AbstractExperiments of dynamical high pressure using shock waves are very effective to study physical properties of material under super-pressure. A shock wave experimental study on Damaping olivine with pressure from 10 to 45 GPa is presented in this paper. Combining previous work about isothermal equation of state for olivine, the temperature in experimental process is determined. The temperatures range from dozens of degree to 800 ℃ when the pressures of our experiments are between 10 and 30 GPa. The density variation with pressure is obtained from our experiments which ranges from 3.627 to 4.009 g·cm-3. According to the recover experiment of the sample and estimated temperatures under experimental pressures, it is derived that the phase transition during our experimental process under pressures of 30 GP did not occur. Meanwhile, the parameters for equation of state are determined. Finally, the geodynamical implication of the experimental results to interior material movement in mantle is discussed, i.e. cold slab with metastable olivine is easily to sink into the mantle′s transitional zone.

KeywordsDynamic high-pressure; Damaping olivine; Equation of state; Density

陈祖安， 袁贤昊， 黄晓葛等. 2016. 大麻坪橄榄石冲击波实验研究与高压态物态方程参数的确定.地球物理学报，59(1):152-156,doi:10.6038/cjg20160112.

Chen Z A, Yuan X H, Huang X G, et al. 2016. A shock wave experimental study on Damaping olivine and estimation of its parameters for equation of state.ChineseJ.Geophys. (in Chinese),59(1):152-156,doi:10.6038/cjg20160112.