数学思想方法在解析几何教学中的应用

荣李 军（忻州师范学院，山西 忻州 034000）



数学思想方法在解析几何教学中的应用

荣李 军
（忻州师范学院，山西 忻州 034000）

摘 要：本文阐述了在解析几何教学中运用数学思想方法的重要意义，探讨了几种常见的数学思想方法在解析几何教学中的渗透与应用，旨在加强学生对数学思想方法的理解，让学生在解答解析几何题目的过程中做到学以致用。

关键词：数学思想方法；解析几何；教学

结解析几何的教学一直以来都是数学教学中的重难点内容，它要求学生在掌握众多基础知识的同时，学会灵活使用这些基础知识，其中，最高层次的无疑是对数学思想方法的掌握。数学思想方法的使用能够将千变万化的试题化无形为有形，并能透过试题中的复杂信息看到问题的本质以及解决的思路，但是，学生对数学思想方法做到熟练掌握并非易事。为此，如何将数学思想方法更好的渗透并应用在解析几何教学中已成为教育界普遍关注的重要课题。

1　在解析几何教学中运用数学思想方法的重要意义

伴随着数学教学工作的不断进步与发展，数学思想方法不仅是数学教育的精髓，还是联系各类数学基础知识的纽带这一观念已深入人心。在解析几何教学中，学生一旦熟练的掌握了数学思想方法，将会在他们的学习过程中如虎添翼，并为日后工作的开展奠定下良好的基础。

2　常见数学思想方法在解析几何教学中的应用

2.1数形结合思想在解析几何教学中的应用

数形结合思想是解析几何教学中的一个核心思想，它能将解析几何中涵盖的知识结构进行融会贯通，并将空间的几何结构进行有系统的代数化和数量化，从而使几何问题的解答形成一个完整的链条，便于学生将复杂的问题简单化，抽象的问题具体化，让学生在面对几何问题时能够正确无误的解答。数形结合思想是通过数据与图形相结合的一种方法，它能直观透彻的分析出几何问题的所在，并能将图形性质的问题转化为数量性质的问题来解决，或将数量性质的问题转化为图形性质的问题来处理。

例1：方程lg x=sin x的实根的个数为（）

A.1个 B.2个 C.3个 D.4个

这一例题单从题目中来看是无法得出最终答案的，但若使用数形结合思想，在同一坐标系中画出y=lg x以及y=sin x的图象，就能清晰的得出这个方程的实根有3个。（如图1所示）

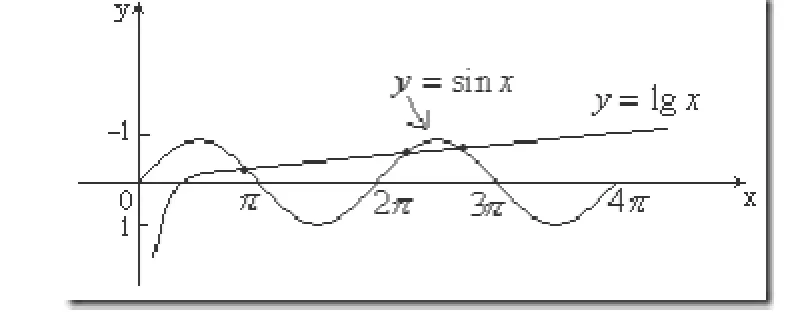
图1　lg x=sin x

2.2化归思想在解析几何教学中的应用

所谓的化归思想是转化与归结思想的简称，它能将复杂的、有待处理的问题，通过某种转化方式，归结到简单的、易处理的或者已经能解决的问题中去，最终达到解决原有问题的效果。［2］化归的基本思想也可用流程图来表示（如图2所示），即以A作为有待解决的问题，B作为简单易处理的问题，我们可以通过某种数学知识内的转化方法，将有待解决的问题A归结为简单易处理的问题 B，并通过问题B的解答与分析，从而解答出问题A的结果。

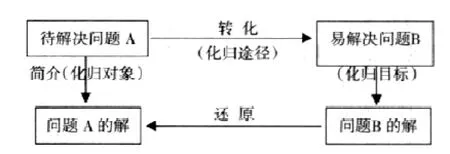
图2　化归思想方法示意图

例2：一个与球心距离为1的平面截球所得的截面面积为π，则球的表面积为（）

A.8√2π B.8π C.4√2π D.4π

解：如图3所示，首先作出球的大圆截面图，由截面小圆的面积为π

即πr2= π，得r = 1

R = √12+ r2 =√2

则S球= 4πR2= 8π

因此，这道题应选B。

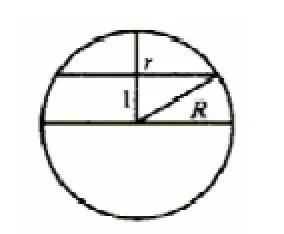
图3　

2.3分类讨论思想在解析几何教学中的应用

分类讨论思想的使用常在不能对问题所给的对象进行统一研究时，需要我们将探讨的对象按照一定的标准进行分类分析，并结合每一类探讨所得出的结果，将其进行有效汇总，最后汇总出来的结果就是该问题的解答。简而言之，分类讨论思想主张“首先化整为零，然后各个击破，最后集零为整。”这样就可以将一个捉摸不定的问题分解成若干个小问题，从而清晰明了的解答出最后的结果。

例3.在平面直角坐标系中，已知矩形AB CD的长为2，宽为1，AB、AD边分别在x轴、y轴的正半轴上，A点与坐标原点重合（如图4所示），将矩形折叠，使A点落在线段DC上。

（Ⅰ）若折痕所在直线的斜率为 k，试写出折痕所在直线的方程；

（Ⅱ）求折痕的长的最大值。解（Ⅰ）（1）当k＝0时，此时A点与D点重合， 折痕所在的直线方程y＝1/2。

（2）当k ≠0时，将矩形折叠后A点落在线段CD上的点为G（a，1） 所以A与G关于折痕所在的直线对称，有kOG·k＝-1，1/a·k＝-1→a＝-k，故 G点坐标为 G（-k，1），从而折痕所在的直线与OG的交点坐标（线段OG的中点）为M（-k/2，1 /2），折痕所在的直线方程y-1/2＝k（x+k/2），即y＝kx+k2/2+k/2。

由（1）（2）得折痕所在的直线方程为：k=0时，y=1/2；k≠0时y＝kx+k2/2+k/2

（II）（1）当k≠0时，折痕的长为2；

（1） 当 k≠0时， 折痕所在的直线与坐标轴的交点坐标为N （0，k2/2+1/2），P（-k2/2k+1/2k，0）

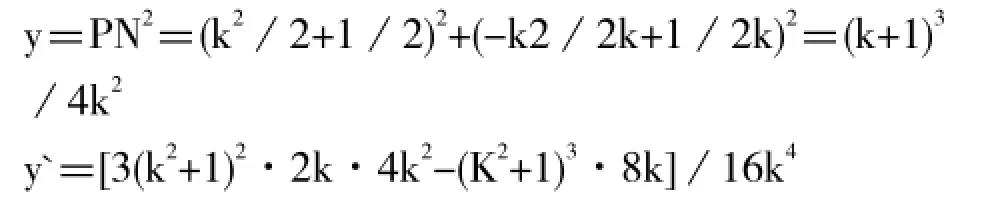
∴PNmax＝27/16＜2

所以折痕的长度的最大值2。

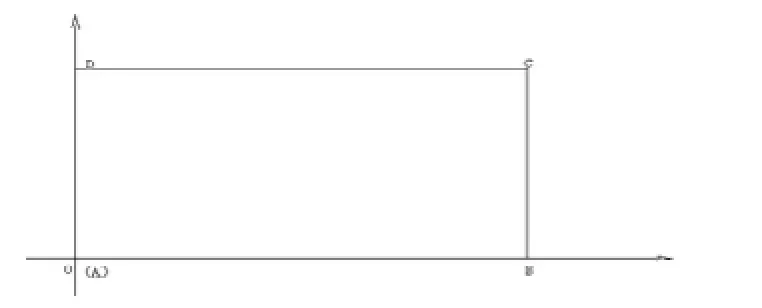
图4　

3　结束语

综上所述，数学思想方法在解析几何教学中的应用，不仅有助于数学教师教学工作的开展，还有利于学生解答几何问题，并对学生的知识素养以及思维能力的培养产生着重要影响。因此，在数学教学中，教师应当注重数学思想方法在教学内容中的渗透，帮助学生熟练的掌握数学思想方法，让学生学会在处理问题时将数学知识贯彻到解题过程中，从而促进数学教学课堂质量以及学生解题能力的有效提高。

参考文献：

［1］马淑云，王阳.解析几何教学中强化数学思想方法刍议［J］.南阳师范学院学报.2011（03）:87-91.

［2］李菲.谈解析几何中几种常见的数学思想方法［J］.数理化解题研究（高中版）.2012（12）:40.

（责任编辑：张时玮）

中图分类号：G633.65

文献标识码：A

doi:10.3969/j.issn.1672-7304.2016.01. 147

文章编号：1672–7304（2016）01–0313–02

作者简介：李军（1981-），男，山西忻州人，研究方向：解析几何教学。

Application of mathematical methods in the teaching of analytic geometry

LI Jun
（Xinzhou Teachers College， Xinzhou Shanxi 034000）

Abstract:This paper described the in analytic geometry teaching in the use of the significance of mathematical thought and method， and discusses the several common mathematical thought and method in analytic geometry teaching penetration And application to enhance the students understanding of mathematics thinking method， let the students in solving analytic geometry problem in the process of make use of the knowledge.

Keywords:Mathematical thinking； Analytic geometry； Teaching