有限元强度折减法在桩锚板支护体系力学分析中的应用

杨　柳

(四川汶马高速公路有限责任公司， 四川成都 610031)



有限元强度折减法在桩锚板支护体系力学分析中的应用

杨柳

(四川汶马高速公路有限责任公司， 四川成都 610031)

【摘要】在介绍有限元强度折减法基本原理的基础上，以某路堑边坡加固工程为研究背景，设置8种工况，采用有限元强度折减法分析采用桩锚板支护体系加固边坡过程中边坡稳定性和支护桩内力。计算结果表明：有限元强度折减法能够较好地分析桩锚板支护体系的加固效果和桩身内力变化；随着支护桩和锚索的施工，桩锚板支护体系对边坡的加固效果十分明显；由于锚索的作用，桩锚板体系中桩的弯矩比传统抗滑桩减小了31.7 %。

【关键词】桩锚板支护体系；有限元强度折减法；安全系数；弯矩；Plaxis

桩锚板支护体系是一种由桩、锚索(或锚拉板)、桩间挡土板组成的边坡支挡结构。由于桩锚板支护体系在传统抗滑桩的基础上设置预应力锚索，并在桩与桩之间设置挡土板，将普通抗滑桩的被动受力状态转化为主动受力，从而达到减小桩身内力、截面尺寸和埋深的目的，节省工程造价，特别适应于边坡高度较大(大于10 m)的工程。该种支护体系已在我国铁路和公路边坡治理、路堤路堑挡墙工程中广泛应用，关于其内力计算的理论成果已十分丰富[1-5]。但由于理论方法都是基于一定的假设条件，所得计算结果和实际工程情况还存在一定的差异，因此难免会出现一些预料不到的情况，有可能会导致严重的工程事故。为能够给桩锚板支护体系设计提供支撑，可采用有限元方法建立数值模型，通过数值模拟方法对桩锚板支护体系进行内力分析，使其计算结果作为理论计算结果的一种补充。

目前在边坡工程稳定性分析中应用较多的是有限元强度折减法，该方法是英国威尔士大学Zienkiewice教授于1975年提出的一种边坡稳定性分析方法[6]，通过对边坡岩土体力学参数进行折减使其达到极限状态，从而确定边坡的安全系数 。国内郑颖人院士[7]首先将强度折减法引入岩土工程领域，对均质边坡稳定性进行分析，取得了比较理想的成果。近年来，有限元强度折减法在非均质边坡中的适用性研究也有了新的进展[8-10]，但是对设置支护结构的边坡工程进行有限元强度折减法分析的研究成果还鲜见报导。针对上述研究现状，以某城市道路工程桩锚板支护工程为研究对象，采用有限元强度折减法对不同阶段桩锚板支护体系的受力进行分析，并将计算结果与试验实测值进行比较，分析有限元强度折减法在桩锚板支护体系力学特性分析中的适用性。

1有限元强度折减法简介

1.1基本原理

所谓强度折减，就是在有限元计算中将岩土体抗剪强度参数c、φ值按一定的折减系数逐渐降低直到模型达到破坏状态为止[7]。此时对应的折减系数就是边坡的强度储备安全系数，即有：

(1)

式中：c、φ为折减前土体的黏聚力和内摩擦角；c′、φ′为折减后土体的黏聚力和内摩擦角；F为折减系数。

1.2屈服准则

现有岩土工程有限元数值分析中常采用Mohr-Coulomb准则(简称M-C准则)，但是M-C准则屈服面在主应力空间中是一个不规则六角形截面的角锥体，在π平面上的图形为不等边六边形，存在尖顶和棱角。M-C准则在三维应力空间中屈服面的这种角隅性质给数值计算带来了困难。为了克服M-C准则屈服面的角隅性质，常用屈服面为圆锥表面的Drucker-Prager准则(简称D-P准则)近似逼近M-C准则[11]。根据D-P准则屈服面与M-C准则的相对位置，D-P准则有多种表达形式[12-13]。在本文的分析中采用内切圆D-P准则来逼近M-C准则，对应的内切圆D-P准则表达式如下：

(2)

2桩锚板支护体系工程实例分析

2.1工程概况简介

某路堑边坡体为剥蚀丘陵形成的斜坡地貌，坡高为7～16 m，边坡土层主要分为表层黏土和粉质黏土、全风化砂/泥岩、强风化砂/泥岩和中等风化砂/泥岩。土层物理力学性质如表1 所示。设计拟采用多支点桩锚板支护体系，共设有支护桩72根。桩身截面尺寸为1.5 m×2.5 m(平行于路线方向为1.5 m，垂直于路线方向为2.5 m)，两桩的中心间距为5.5 m，两桩净间距为4 m，嵌固深度为5～7 m。桩身材料为C30混凝土。根据桩长不同设置不同排数和不同类型的预应力锚索，其中A型桩长为20 m，每排设置2孔锚索；B型桩长25 m，每排设置3孔锚索；C型桩长25 m，每排设置4孔锚索。锚索锚固段长度均为10 m，锚索材料为3φ15.2 mm钢绞线，强度为1 860 MPa。支护桩之间为30 cm厚C30混凝土挡板，除顶部的混凝土挡板为直立外，其余均为部分直立，部分曲线型(弧形)。混凝土挡板左右两侧镶嵌在支护桩内，中间部分有多排锚杆支护。锚杆为φ28 mm螺纹钢筋，长度为9 m。本工程的桩锚板支护体系如图1所示。

表1　土层物理力学参数

图1　桩锚板支护体系

2.2有限元模型的建立

为了使有限元分析具有代表性，同时保证计算分析的效率，在此采用Plaxis进行二维有限元分析。建模时选取桩长最长的桩所在边坡剖面为研究对象，此时边坡坡高约为13 m，桩长为25 m，锚固段深度为6 m。根据Plaxis软件的规定，水平方向为x方向，向右为正；竖直方向为y方向，向上为正。为了减小边界效应对计算结果的影响，在建立有限元模型时所采取的范围如下：坡脚到左边界的距离为1.5H(H为边坡高度)，坡顶到右边界距离为3.3H。由此建立的边坡几何模型如图2所示。

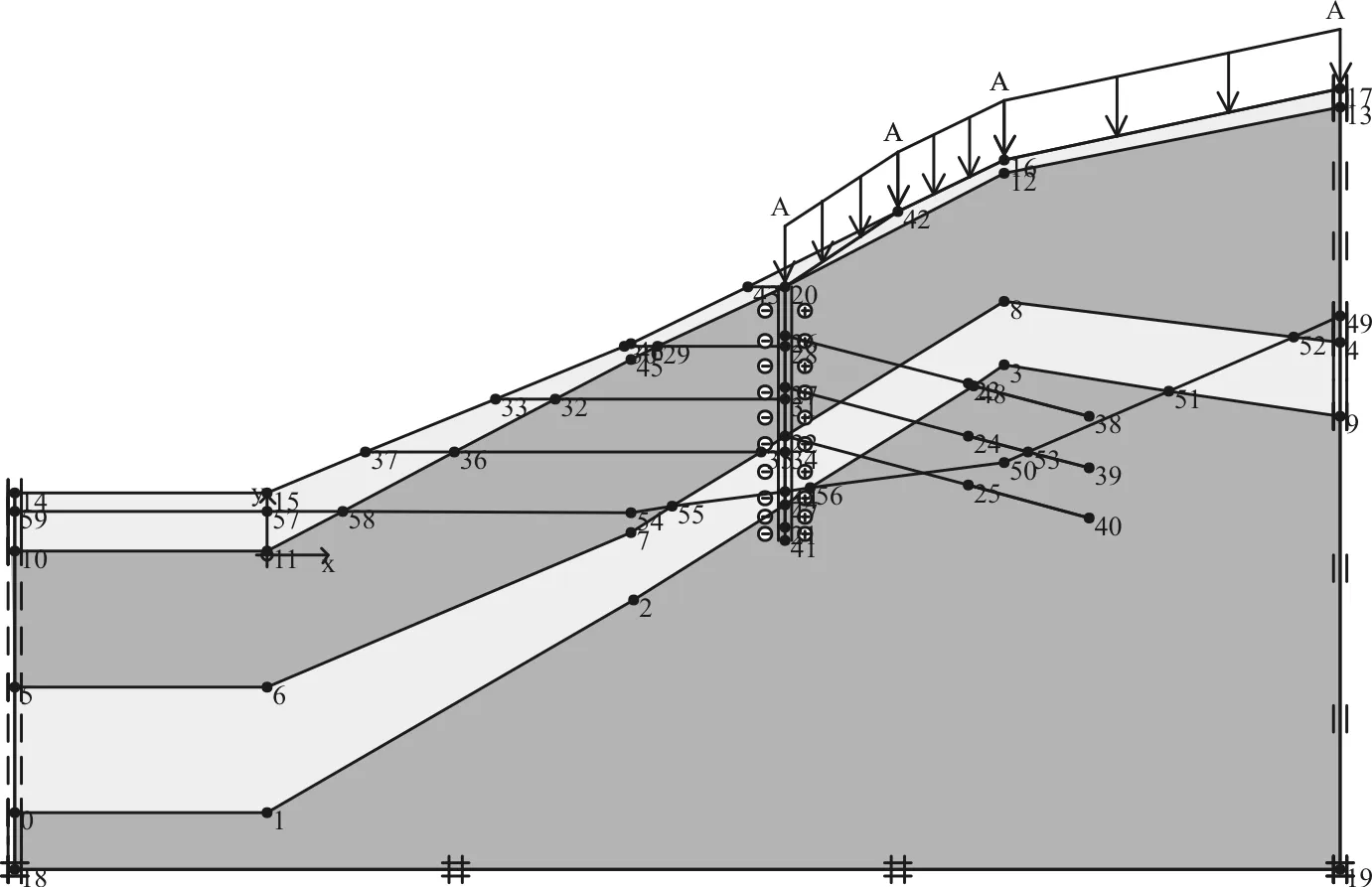
图2　边坡几何模型

在几何模型建立之后，采用Plaxis网格生成器自动划分网格。为了精确分析锚索和桩的内力，在锚索锚固段和桩土截面处局部加密网格。整个模型共划分有799个15节点三角形单元，6 653个单元节点。另外，桩采用线弹性梁单元来模拟，按照抗弯刚度等效原理，将桩沿布置方向作连续化处理；锚索自由段采用锚杆单元模拟，锚固段以土工格栅单元模拟；桩土接触界面采用Goodman接触单元模拟，桩-土界面折减系数取0.8。考虑到可能出现的荷载作用，在进行模拟计算时桩顶至右边界范围内考虑5 kN/m2的均布荷载。

2.3模拟工况设计

为了对桩锚板支护结构体系加固边坡的作用及自身内力进行分析，在此考虑了天然边坡和支护结构施工过程引起的边坡稳定性变化，设计了8种工况，分别如表2所示。

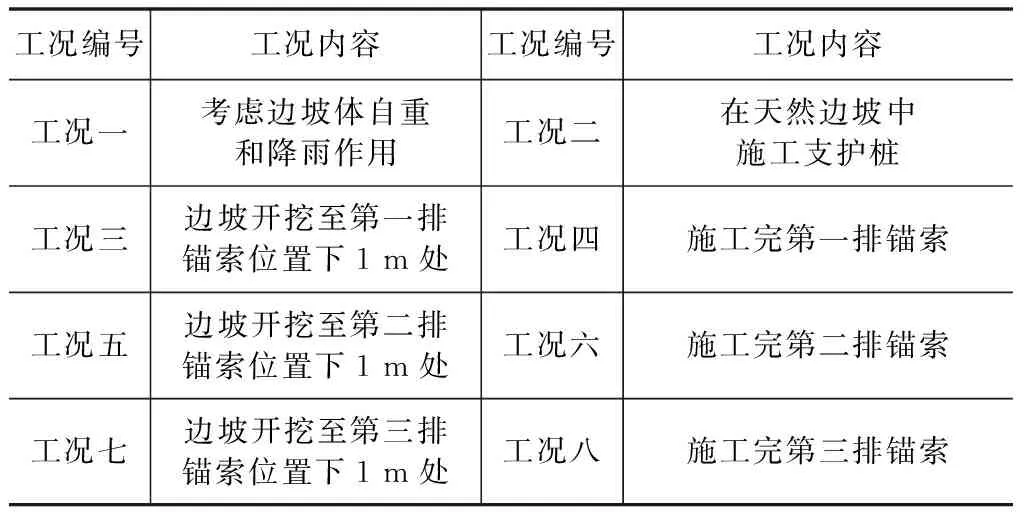
表2　工况设计

3计算结果分析

尽管在有限元强度折减法中塑性区贯通是判断边坡失稳的重要判据，但是塑性区贯通的判据缺乏客观的判断指标，更多的依赖于人的主观判断。因此在本文中采用数值不收敛作为边坡的失稳判据，并选取增量位移作为边坡失稳的辅助判据，它可以方便地描绘出边坡失稳时滑动面的大致范围和形状，然后通过对表2所示8种工况进行分析，得到了该路堑边坡在天然和施工过程中的稳定情况，并能获得支护桩在不同施工阶段的内力情况。下面将分别针对这两类计算结果进行分析。

3.1稳定性分析

以增量位移作为边坡稳定与否的辅助判据，通过边坡位移的发展趋势可以较好地判断边坡是否处于稳定状态，8种工况下的增量位移分布如图3所示，相应的边坡稳定系数如图4所示。由图3、图4可知：天然边坡在自重和降雨作用下，在边坡坡脚处出现浅层滑动；工况二中，在开挖边坡和支护桩孔的过程中边坡临空面出现较大的相左下的位移，此时说明在边坡浅层出现以相临空面大变形为主的垮塌，因此需及早将支护桩浇筑；在随后开挖施工三排锚索的过程中，边坡的稳定系数随开挖而降低，又随着锚索施工而增加，这说明锚索对边坡稳定性有着积极作用。

(a)工况一

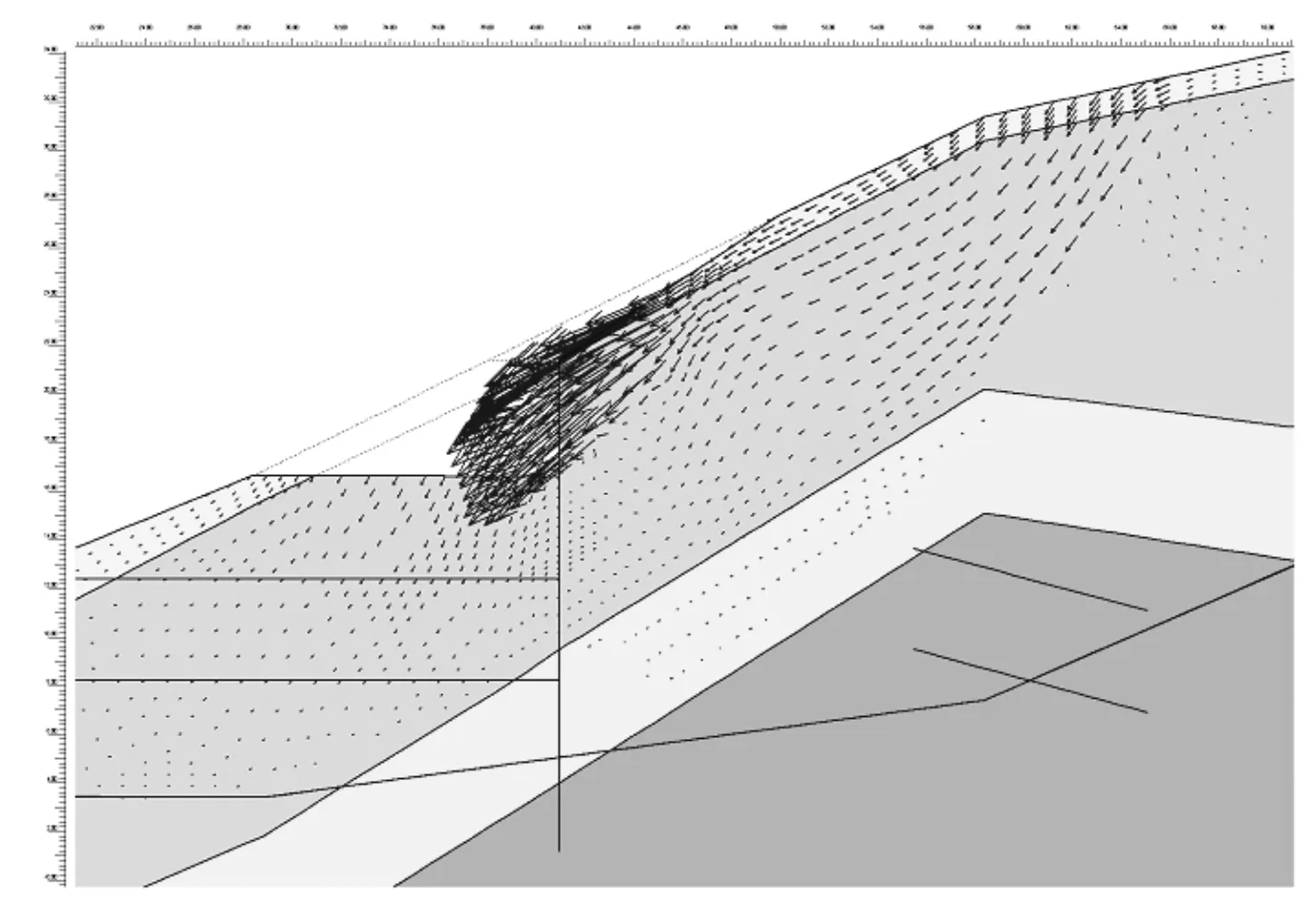
(b)工况二

(c)工况三

(d)工况四

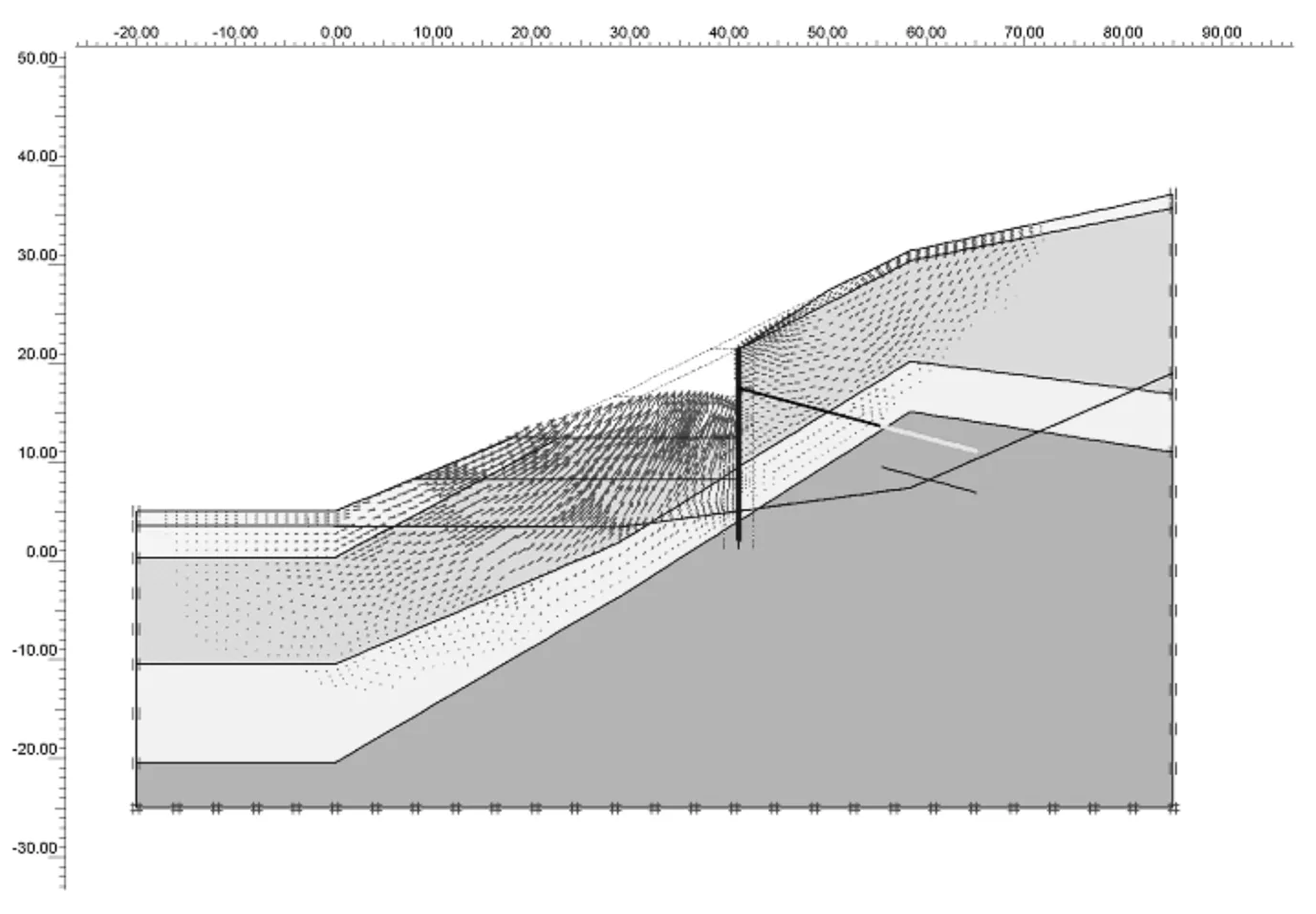
(e)工况五

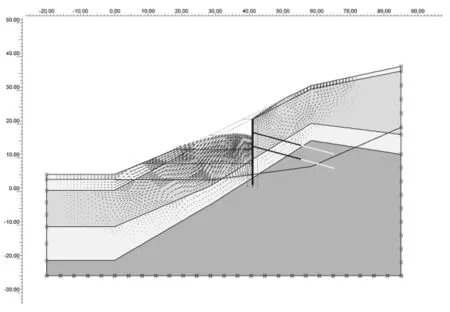
(f)工况六

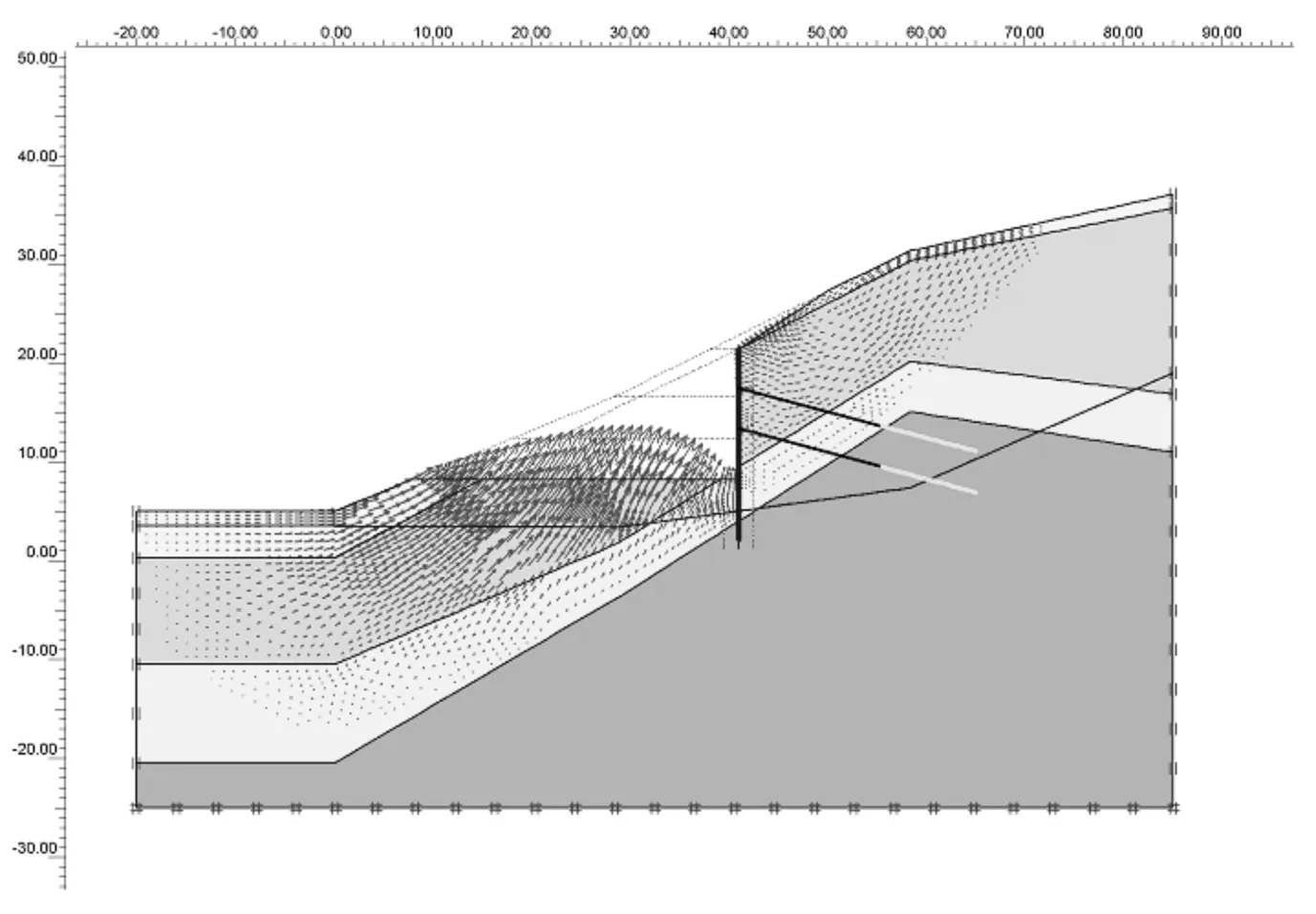
(g)工况七

(h)工况八

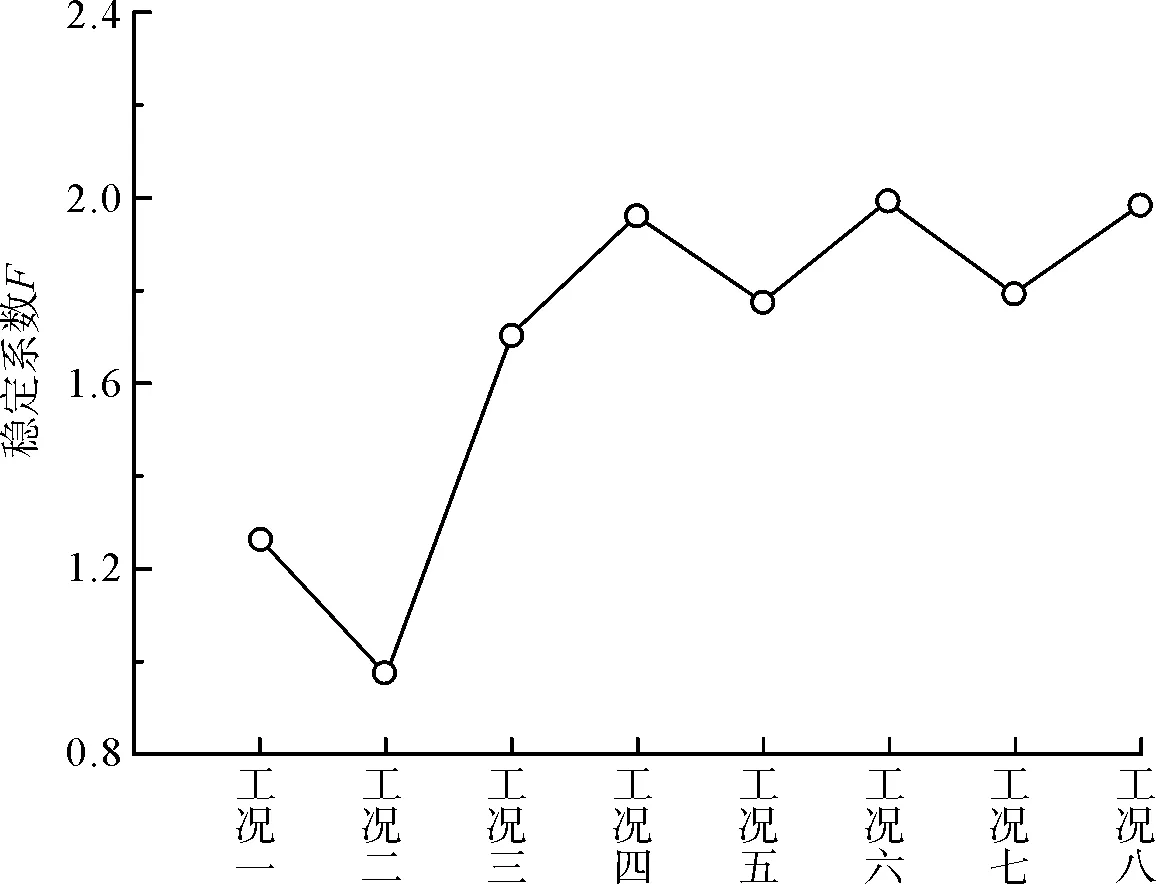
图4　各种工况下边坡稳定系数变化规律

3.2桩身弯矩分析

对支护桩而言，由土体下滑力产生的弯矩是设计支护桩的主要内力，因而在此主要针对工况三至工况八6种情况下的支护桩桩身弯矩变化过程进行分析。各工况下的桩身弯矩分布情况如图5所示，其中不同工况下桩身最大弯矩变化规律如图6所示。由图5、图6可知：支护桩的弯矩随着开挖深度的增加而增大，当预应力锚索施工完成后，支护桩的弯矩相应减小，此时锚索已经发挥作用，锚索和支护桩形成了联合结构，共同抵抗由开挖卸荷引起的岩土体压力；当边坡继续开挖时，桩身弯矩同上一开挖步相比，略有减小；整个开

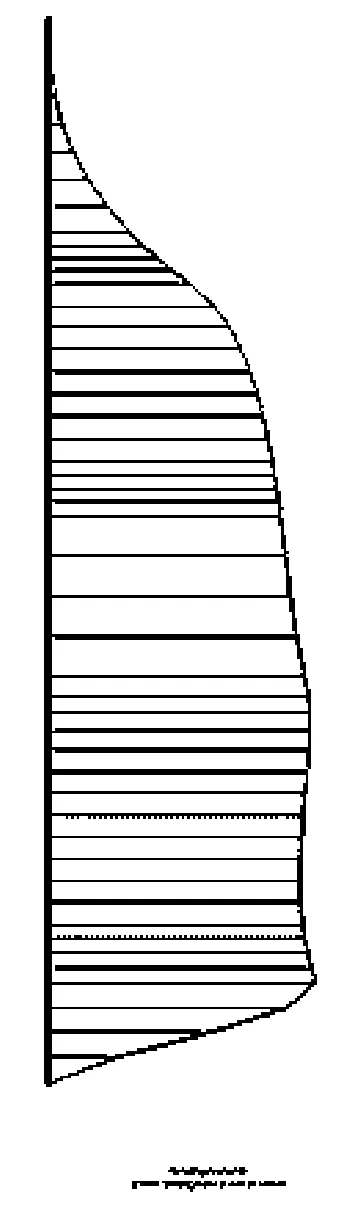
(a)工况三

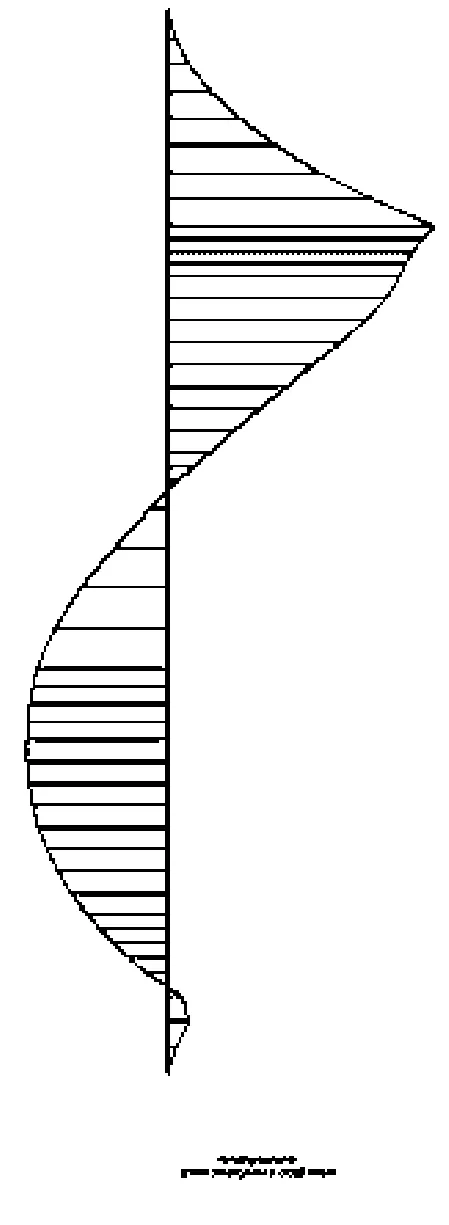
(b)工况四

(c)工况五

(d)工况六

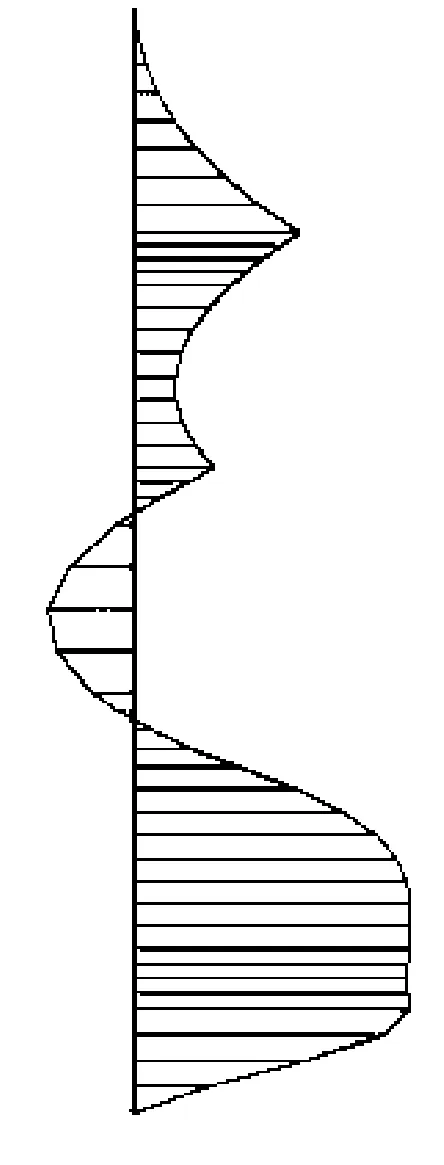
(e)工况七

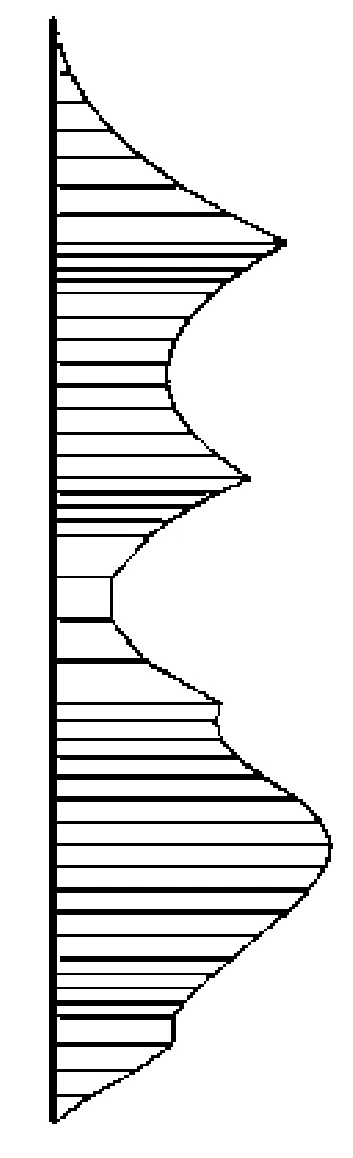
(f)工况八

挖过程结束后，桩身弯矩最大值由边坡刚开始开挖的2 288 kN·m(此时桩未施加锚索及预应力，可看作悬臂状态)减小为1 565 kN·m(桩由悬臂状态转为多支点锚拉状态)，减小了31.7 %,由此可见在多点预应力锚索的作用下，桩身弯矩同普通抗滑桩相比大大减小，同时也减小了桩的侧向变形；计算结果表明边坡在使用多支点锚拉桩支护时，在施加较小的锚索的预应力的情况下，就可减小支护桩的尺寸，同时又能明显地减少桩身的弯矩。

图6　各工况下支护桩最大桩身弯矩

同时，将计算结果与现场监测结果进行比较发现：当施工完成后，按有限元强度折减法计算的桩身最大弯矩为1 565 kN·m，而实测结果为1 700 kN·m，两者误差不到10 %，这说明有限元强度折减法可以较好地分析桩锚板支护体系的内力情况，所得结果具有可信度。

4结论

针对桩锚板支护体系加固边坡工程，根据支护体系施工过程分别设置了8种工况，采用有限元强度折减法，分别对8种工况下的边坡进行稳定性和桩身内力分析。计算结果表明：有限元强度折减法能够较好地分析桩锚板支护体系的加固效果和桩身内力变化；随着支护桩和锚索的施工，桩锚板支护体系对边坡的加固效果十分明显；由于锚索的作用，桩锚板体系中桩的弯矩比传统抗滑桩减小了31.7 %。

参考文献

[1]周德培,王建松. 预应力锚索抗滑桩内力的一种计算方法[J].岩石力学与工程学报, 2002, 21(2): 247-250.

[2]刘小丽.新型桩锚结构设计计算理论研究[D]. 成都: 西南交通大学, 2003.

[3]曾德荣, 凌天清, 范草原. 预应力锚索在滑坡治理中的设计与施工[J]. 水文地质工程地质, 2000 (5): 51-54.

[4]曾德荣, 李霖. 抗滑桩锚索联合体系特性研究[J]. 重庆交通学院学报, 2001, 20(2): 79-82.

[5]门玉明, 邓军涛, 李金湘. 锚索抗滑桩设计中的几个问题探讨[J]. 公路交通科技, 2005, 22(6): 52-54.

[6]Zienkiewicz O.C., Humpheson C. and Lewis R.W.. Associated and non-associated visco-plasticity and plasticity in soil mechanics[J]. Geotechnique, 1975, 25(4): 671-689.

[7]郑颖人，赵尚毅.有限元强度折减法在土坡与岩坡中的应用[J].岩石力学与工程学报，2004，23(19)：3381-3388.

[8]刘作飞，王多垠，汪承志.强度折减有限元法在加固桩基码头岸坡中的应用[J].中国港湾建设，2008(5)：13-16.

[9]杨有成，陈新泽，郭凯,等.对强度折减法分析非均质边坡稳定性的适用性研究[J].中国水运，2008，6(1)：56-57.

[10]赵旭.隧道洞口段边仰坡失稳机理及计算研究 [D].上海：同济大学,2009.

[11]苏继宏，汪正兴，任文敏，等.岩土材料破坏准则研究及其应用[J].工程力学，2003，20(3)：72-77.

[作者简介]杨柳(1980～)，男，硕士研究生，工程师，从事高速公路建筑管理工作。

【中图分类号】TU94+2

【文献标志码】A

[定稿日期]2015-11-13