直线轴承圆度误差评定测量点数的优化

龚玉玲,武美萍，徐晓栋，蒋飞

(1.泰州学院 船舶与机电工程学院，江苏 泰州 225300；2．江南大学 机械工程学院 江苏省食品先进制造装备技术重点实验室，江苏 无锡 214122；3．泰兴轴承厂，江苏 泰州 225400)

在轴承检验中，圆度误差是重要的检测指标[1-3]，圆度测量需对能够反映被测对象几何特460028)；2015年度泰州学院校级科研课题(TZXY2015BK T011)

征的要素进行离散数据采集，并通过计算机技术分析处理[4-5]，进行离散数据信息处理的圆度误差评定常用4种方法：最小区域法(MZC)、最小二乘法(LSC)、最大内切圆法(MIC)和最小外接圆法(MCC)[6-7]。由于圆度误差评定的目标函数为非线性函数，求解较困难，可采用遗传算法(GA)[8]，标准粒子群优化算法(PSO)[9]及协同粒子群优化算法CPSO[10]等不断提高后期圆度误差评定的效率和精度，但对前期数据采集方法和采集点数的研究却较少。

文献[11]发现测量点数对圆度误差有较大影响，却没有深入进行优化分析。目前的实际测量主要依据测量人员的经验，测量数据较少时测量效率会有所提高，但后期圆度误差评定结果变化较大；若要保证后期圆度误差评定结果的稳定性和精度，则需选择较多的测量点数，会导致测量效率大大降低，影响测量进度。因此，在上述研究的基础上，尝试对测量点数进行优化，以达到测量精度与测量效率的优化配置。

1 圆度误差模型的建立

最小二乘法理论成熟，精度较高，在圆度误差评定中使用最广泛[12]，且测量点数为偶数、对称分布时，圆度误差评定方程可由非线性方程转化成线性方程，使误差评定难度大大降低。采用最小二乘法进行圆度误差评定的原理如图1所示。

采用三坐标测量机(LK-G90C)采集数据，LK-G90C的长度示值精度为(2.5 +L/300)μm，采样精度为3.0 μm，测量温度为20 ℃，对圆度数据均匀采集n个点Pi(xi,yi)(i=1,2,…,n;n为偶数)，确定初始圆心(x0,y0)和初始半径R0，构造圆方程为

(xi-x0)2+(yi-y0)2=R2，

(1)

则由最小二乘法[13]拟合圆的圆心和半径为

(2)

(3)

以初始圆心(x0,y0)和初始半径R0为基础，对圆度进行均布数据采集，设实测点为Pj(xj,yj) (j=1,2,…,m;m>n且m为偶数),实际测量点的坐标为

(4)

则该圆周修正后的圆心和半径为

(5)

(6)

圆度误差为

(7)

则最小二乘法(LSM)进行圆度误差评定的模型为

2 圆度误差模型类型的判断

以直线轴承为例进行试验验证。直线轴承结构如图2所示，规格见表1，其内外圆柱面为主要配合部位，误差检测要求较高。

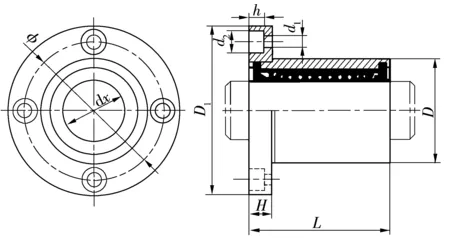
图2 直线轴承结构图

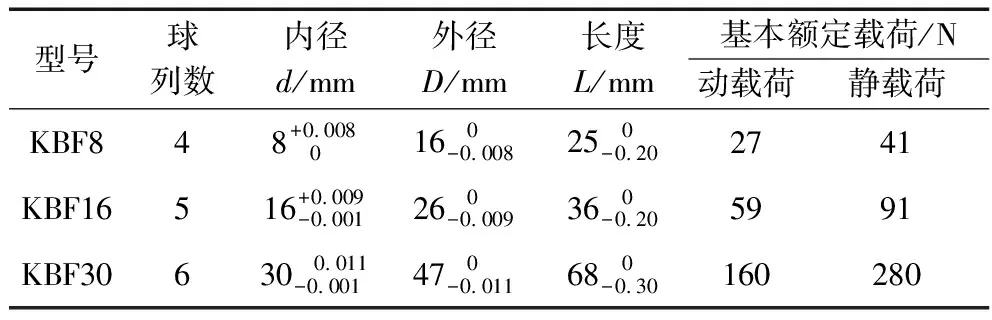
表1 直线轴承规格表

以外圆柱面的圆度为例，采用三坐标测量机进行测量，内圆柱面的圆度测量方法相似。采集直线轴承外圆柱面圆度的不同测量点数，并对每套轴承分别采集4组数据进行试验(表2)，最后根据采集的数据由(7)式建立圆度误差模型。

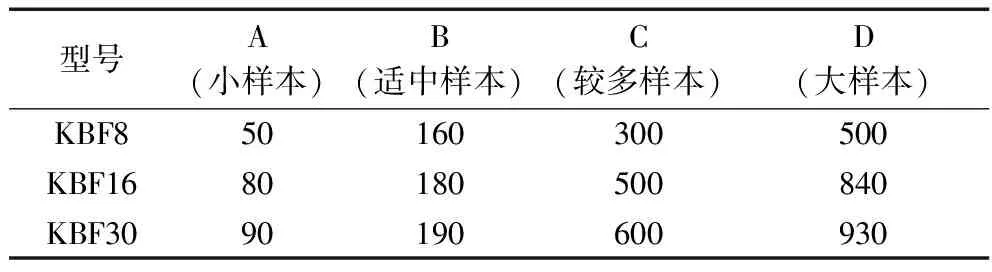
表2 测量点数

2.1 基于图形初定圆度误差模型类型

常见的模型类型有正态分布、指数分布、均匀分布等，统计图定性分析可采用直方图、茎叶图、箱式图、P-P图，Q-Q图等方法。具体步骤是根据离散点分布情况，采用适当的曲线尽量拟和逼近该离散点。以直方图为例，当直方图中间高、两边低，左右对称呈“钟形”曲线，可定性判断近似服从正态分布。

以圆度误差εj为横坐标，测量点数概率为纵坐标，绘制KBF8的4组数据直方图如图3所示。

图3 圆度误差直方图

从直方图可以看出，当测量点数较少时，正态分布特征不显著，测量点数超过160及以上时基本趋于正态分布。

2.2 统计指标定量检验圆度误差模型

目前常采用国际通用的统计分析软件(SAS，SPSS等)进行指标统计计算。以SAS为例，常见的正态检验方式有W检验和K-S检验[15-16]。

2.2.1 Shapiro-Wilk正态性检验(W检验)

W检验的步骤如下：

1)将n个样本值由小到大进行排序，即x(1)≤x(2)≤…≤x(n)。

2)计算W检验的统计量

(9)

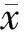
3)假定显著性水平值为α，根据统计量W和样本容量n，由统计量W的分位数表，确定相对应的概率值Pr。

4)当Pr≥α，接受假设，则符合正态分布；反之，当Pr<α，则拒接假设，不符合正态分布。

其他的判断方式与W检验的判断方式类似，主要区别是检验统计函数不同。SAS软件规定n<2 000时，以W检验结果为准。

2.2.2 Kolmogrov-Smirnov检验(K-S检验)

K-S检验采用的经验函数Fn(x)为

，(10)

则K-S检验的统计指标为

(11)

SAS软件规定n≥2 000时，以K-S检验结果为准。

2.2.3 评定结果

由表2可知，测量点数n小于2 000，故以W检验结果为准，正态检验中取显著性水平α=0.05[14]，正态检验及圆度误差评定结果见表3。由表可知，当测量点数较少时，圆度误差模型不符合正态分布，但是超过一定数量后，模型误差分布符合正态分布，继续增加测量点数，圆度误差评定变化很小。

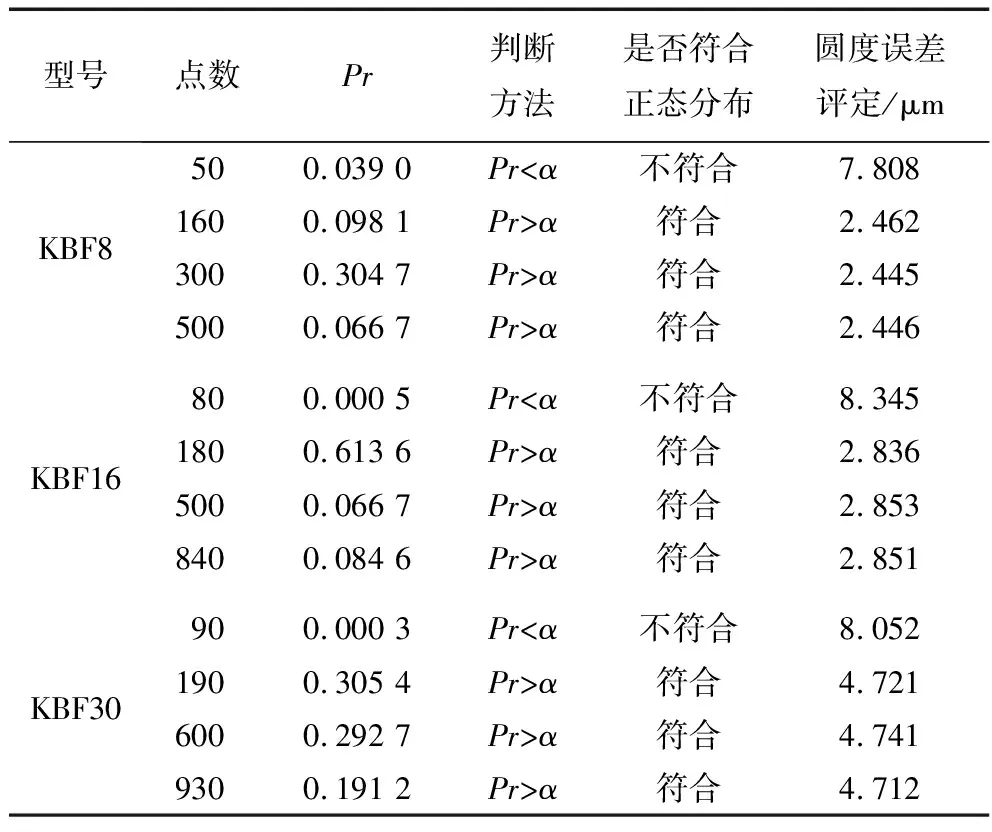
表3 圆度误差评定结果(W检验)

3 最优临界点数的确定

如前所述，当测量点数超过一定数量后，圆度误差模型特征呈现正态分布特征，可根据正态分布特性，采用统计试验确定最优临界点数。为增加最优临界点数的准确性，取最小点数增加步长，因采用最小二乘法进行误差评定时将非线性方程转化成线性方程，故最小增加点数为2，具体试验流程如图4所示。

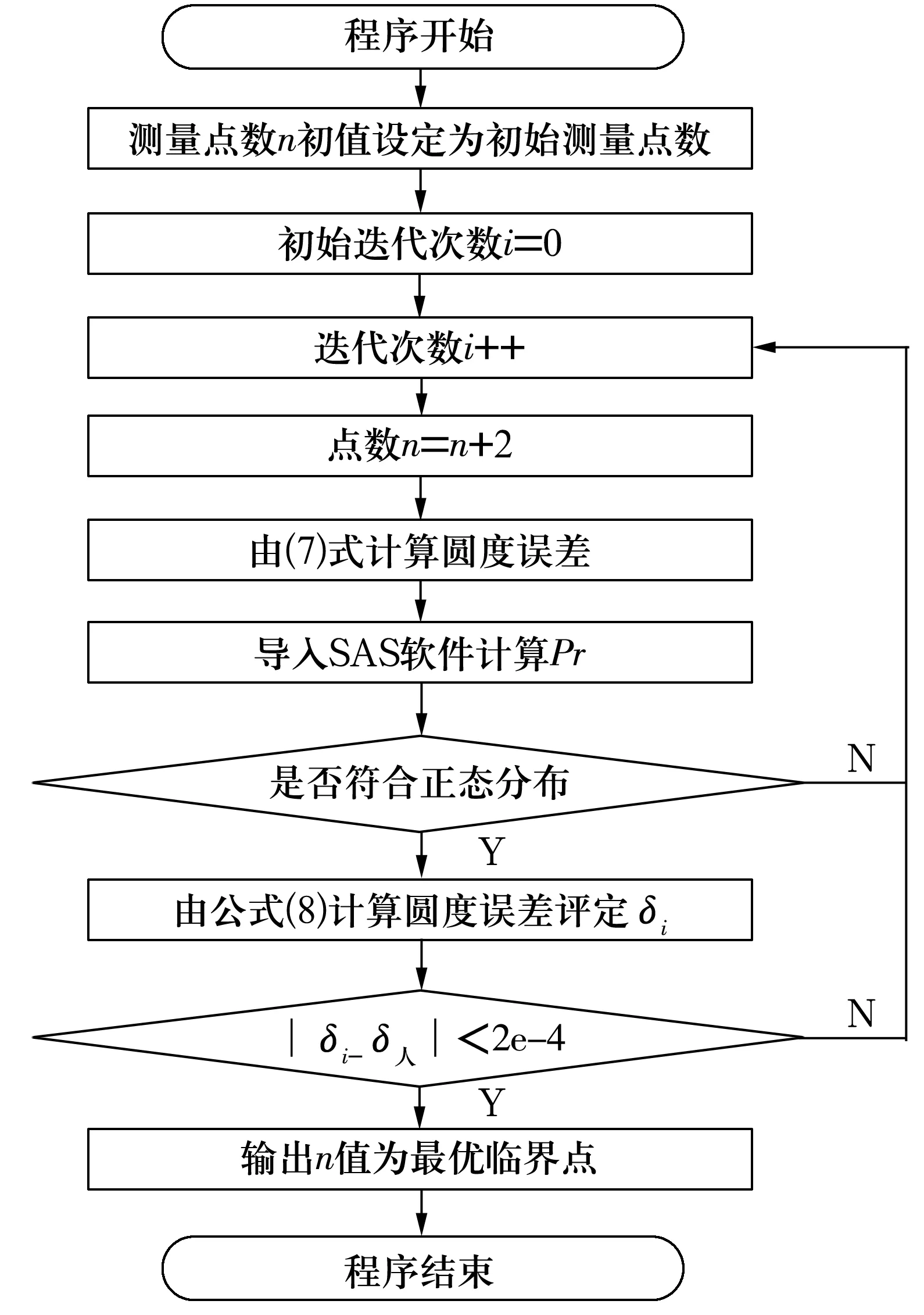
图4 确定最优临界点数流程图

按照图4流程，以直线轴承KBF8为例，首先给定初始测量点数n为50，采用 (4) 式均布取点，每次增加2个点，然后按照 (8) 式进行圆度误差评定，绘制的圆度误差评定统计图如图5所示。从图中可以看出：测量点数在50～108之间，圆度误差评定值变化剧烈。测量点数达到108后，圆度误差评定值稳定在2.49 μm，与人工经验测量的圆度误差评定值相近，再增加测量点数时圆度误差评定变化不大。故直线轴承KBF8的最优临界测量点数为108。 同理，可确定KBF16和KBF30的最优临界测量点数分别为126和148，如图6所示。

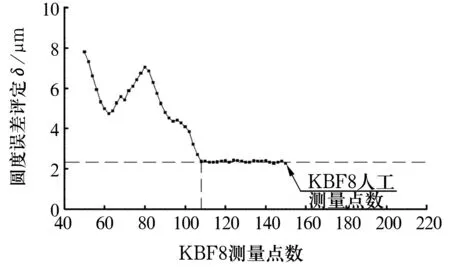
图5 KBF8圆度误差评定统计图

图6 圆度误差评定统计图

最优临界点数与人工经验点数测量方法的结果见表4。由表可知：2种方法的测量误差较小，但最优临界点数测量方法的测量点数明显减少，在不同型号轴承上的测量效率分别提高30%，47.7%和42.1%，而且测量结果稳定可靠，在保证测量精度的前提下有效提高了测量效率。

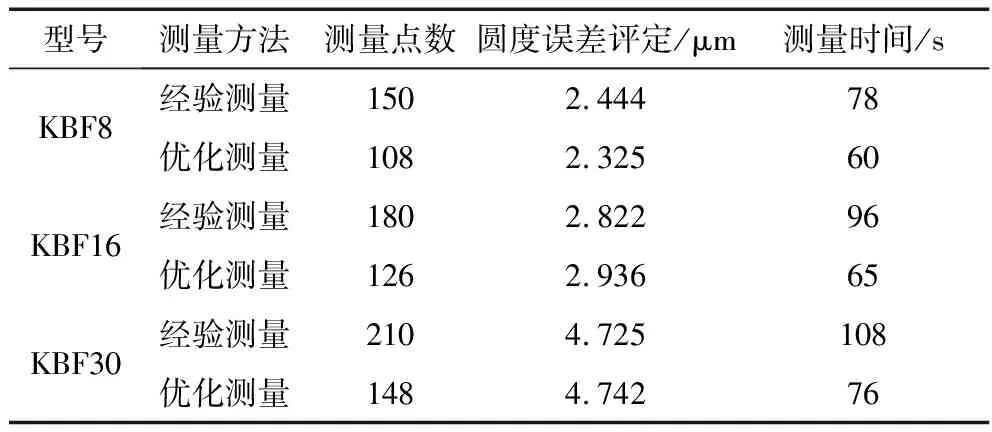
表4 测量结果对比

4 结束语

采用三坐标测量机采集圆度误差数据，基于最小二乘法建立圆度误差模型，最后采用基于正态分布模型的点数优化方法确定最优临界点数，与经验点数测量方法相比，测量精度基本变化不大，但测量效率可提高30%以上。在企业圆度误差测量的实际应用中，该方法测量效率提高明显，测量结果稳定可靠，具有较强的指导意义。