基于ABAQUS和FATIGUE的风电转盘轴承疲劳寿命计算
马振革,陆超,洪荣晶,陈捷
(1.洛阳LYC轴承有限公司,河南 洛阳 471003;2.南京工业大学 机械与动力工程学院,南京 211800)
风电转盘轴承作为风力发电机的一个重要零部件,对质量要求较高。因此,安装使用前必须对轴承疲劳寿命进行估计。Lundberg和Palmgren提出的L-P模型寿命公式在一定程度上解决了中小尺寸轴承的寿命计算问题,但并不适用于大型转盘轴承的计算。针对此,国内外学者提出了复杂工况下的转盘轴承寿命计算修正公式。文献[1]结合风机行业的设计规范与标准,合理利用相关的计算方法得到了转盘轴承寿命的计算公式,具有一定的实际工程应用价值。文献[2]对应力寿命法和应变寿命法作了比较,结果表明应力寿命更适合转盘轴承的疲劳寿命计算。但进一步研究发现,转盘轴承的理论寿命计算方法非常繁琐,且并不适用于所有类型的转盘轴承。因此,文中以四点接触球转盘轴承为研究对象,提出基于ABAQUS和FATIGUE的转盘轴承疲劳寿命计算方法。
1 风电转盘轴承疲劳寿命的计算
1.1 当量动载荷
风电转盘轴承所受外部载荷为轴向力Fa、径向力Fr和倾覆力矩M,作用于转盘轴承几何中心。风电转盘轴承寿命[3-4]没有通用的计算方法,根据Lundberg- Palmgren的疲劳寿命理论[5-7],其计算公式为
(1)
式中:Ca为额定动载荷;Pa为当量动载荷;a1为可靠性寿命调整系数;a2为沟道硬度调整系数;a3为润滑系数;ε为疲劳寿命系数,对于球轴承,ε取为3。
当量动载荷[5]为
(2)
式中:Dpw为球组节圆直径。
1.2 额定动载荷
Lundberg 和 Palmgren将 Weibull损伤概率理论应用于轴承寿命的计算中,并且考虑轴承的尺寸及应力循环次数的影响,在此基础上依据试验结果修正相关系数与指数,球轴承基本额定动载荷为
(3)
式中:Dw为钢球直径;fcm为轴承的材料系数;i为钢球列数;Z为钢球数;α为接触角。
2 基于ABAQUS的转盘轴承接触应力分析
疲劳寿命仿真计算流程如图1所示,主要分为2个阶段,即有限元分析阶段和疲劳寿命仿真阶段。第1阶段是整个计算过程的前提和基础,第2阶段为用疲劳分析软件对有限元分析的结果进行疲劳寿命的计算。
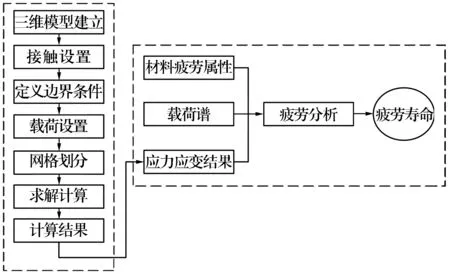
图1 疲劳寿命仿真流程图
2.1 有限元分析
以型号为QNA730-22的转盘轴承为例,其结构尺寸为:球组节圆直径Dpw=730 mm,钢球直径Dw=22.5 mm,钢球数Z=91,接触角α=45°,内沟曲率半径系数fi=0.52。内外圈材料为42CrMo,其力学性能参数为:弹性模量E=206 GPa,抗拉强度Rm=1 080 MPa,屈服强度Re=930 MPa。转盘轴承转速为0.052 r/min。
由于转盘轴承受力复杂,钢球与沟道的接触载荷受多种因素影响,且有限元计算过程极易出现迭代不收敛[8],从而无法得出理想计算结果。因此对模型进行简化:1)不考虑重力的影响;2)不考虑螺栓预紧力的影响;3)忽略对研究目标影响不大的外形特征(如齿形);4)由于对称性,截取半个转盘轴承进行有限元分析,如图2所示。

图2 转盘轴承有限元模型
将转盘轴承模型导入ABAQUS中进行分析,钢球与沟道定义为面面接触,接触性质为法向硬接触,切向摩擦因数为0.04。
在外圈底面上加载全约束边界条件,在两端施加对称边界约束条件。建立一圈刚性元,将内圈上表面耦合于内圈上表面的几何中心点,外部载荷加载在中心点,通过刚性元作用在内圈上。约束与载荷的施加如图3所示,在中心点处施加该转盘轴承所能承受的极限载荷Fa=96 kN,Fr=101.8 kN,M=240 kN·m。

图3 施加载荷与约束
对模型采用六面体C3D8R单元,利用扫略网格划分。由于钢球与沟道之间为接触发生区域,考虑到计算精度以及计算效率问题,对钢球与沟道内侧采用细分网格,其余部位相对较粗,如图4所示。

图4 网格划分
2.2 结果分析
极限载荷下,转盘轴承的应力分布如图5所示,最大应力出现在沟道接触处,为2.442 GPa,这与实际应用中转盘轴承沟道与钢球接触部位经常出现破损、点蚀的情况相符,进一步验证了有限元模型的正确性。

图5 有限元分析结果
3 基于FATIGUE的转盘轴承疲劳寿命分析
3.1 材料的疲劳属性
FATIGUE的材料数据库中没有转盘轴承所用的42CrMo,因此需根据42CrMo的材料属性新建材料数据库,由FATIGUE软件自动生成42CrMo的S-N曲线,如图6所示。
3.2 载荷谱
风电转盘轴承由于其特殊的工作环境,通常并不作连续转动,只是作小角度回转,大多数时间处于锁紧状态。由于随机变化的风速、风向的影响,导致转盘轴承承受交变随机载荷,由此引起的微动磨损造成转盘轴承的疲劳失效。
载荷信息可以使用软件中的时间历程数据库管理器来定义。根据文献[9]中所介绍的转盘轴承载荷谱作为本次疲劳寿命估算的载荷信息,文献中的载荷谱均为雨流计数法简化后一次应力循环中的最大值,并定义其最小值为0。定义最大载荷为1和最小载荷为0的交变载荷,交替频率可以通过转速计算。此外定义的最大载荷及最小载荷只是一个相对量,即载荷值是疲劳分析软件载荷信息中的值与ABAQUS中施加载荷的比值。由于在加载状态下转速为0.052 r/min,转盘轴承的钢球数为91,所以钢球与滚道的接触频率为0.052×91/60=0.078 8。将以上信息输入FATIGEU的载荷信息模块得到如图7所示的载荷信息图。
3.3 结果分析
疲劳寿命计算以材料及零件的应力为基础,采用应力法和疲劳累计损伤理论进行全寿命分析[10],疲劳寿命计算结果如图8所示。
由图8b和图8c可知,主要失效区域集中在沟道与钢球的接触区域。此接触部位的疲劳寿命最短,节点编号为26 375,为3.44×104r,而根据(1)式计算得到的理论疲劳寿命为3.156×104r,两者接近,因此可以用于实际工程之中。
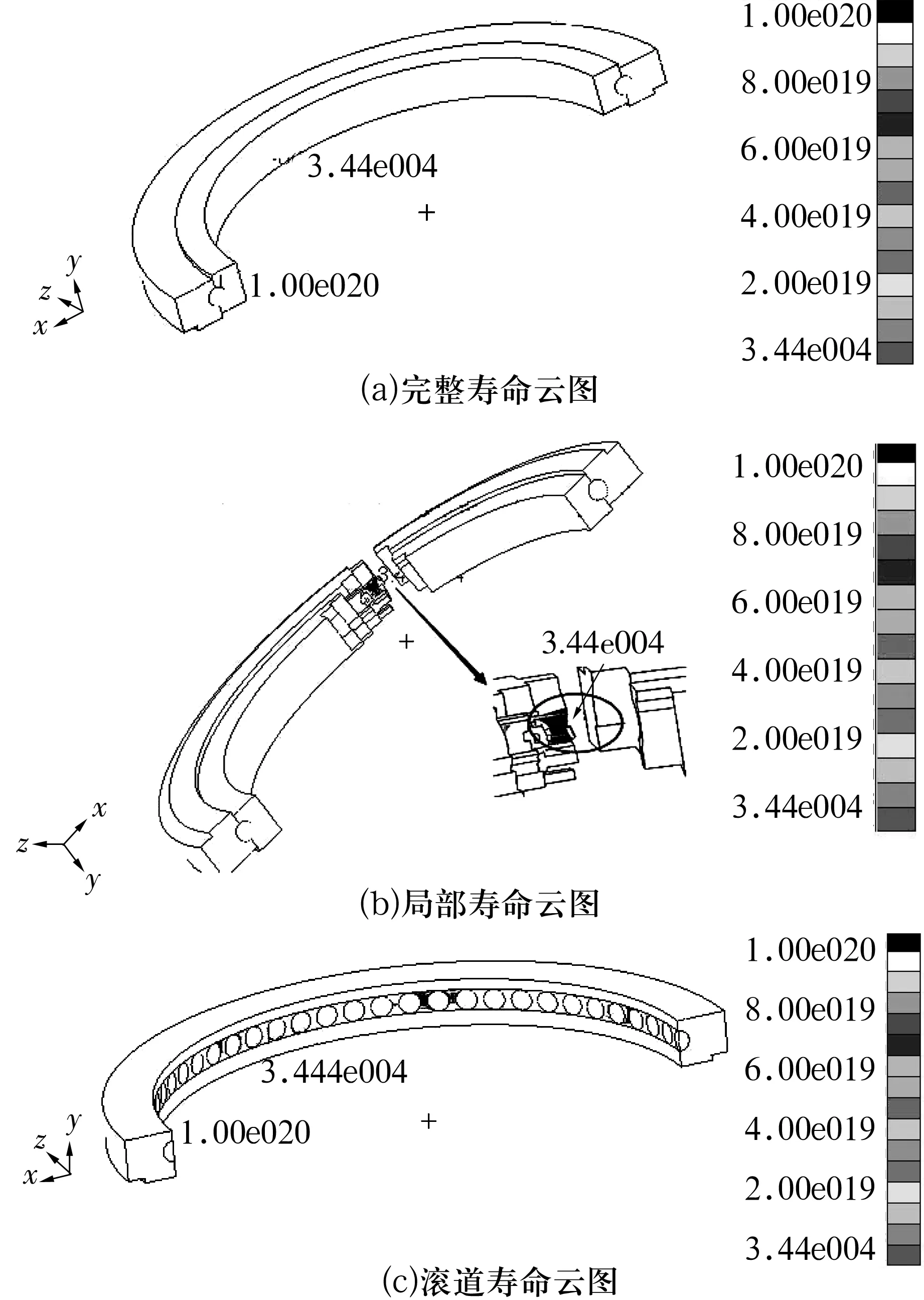
图8 寿命云图
4 结束语
基于ABAQUS提出了简化的转盘轴承有限元模型,再利用疲劳分析软件FATIGUE对转盘轴承进行了寿命预测,得到轴承的疲劳危险区域和寿命云图。对比分析理论计算与疲劳仿真的结果,证明了模拟仿真计算方法对转盘轴承疲劳寿命预测的可行性,具有一定的实际工程应用价值。

