基于振动传递率函数与统计假设检验的海洋平台结构损伤识别研究

刁延松， 徐东锋, 徐　菁,2， 毛　辉,2

(1.青岛理工大学 土工程学院，山东 青岛　266033； 2.山东省蓝色经济区工程建设与安全协同创新中心，山东 青岛　266033)



基于振动传递率函数与统计假设检验的海洋平台结构损伤识别研究

刁延松1，2， 徐东锋1, 徐菁1,2， 毛辉1,2

(1.青岛理工大学 土工程学院，山东 青岛266033； 2.山东省蓝色经济区工程建设与安全协同创新中心，山东 青岛266033)

摘要：由于受激励未知、测量噪声及建模误差等因素影响，基于振动的结构损伤识别结果存在明显不确定性。为此，利用振动传递率函数和统计假设检验进行结构损伤识别研究。用结构损伤前后加速度响应计算振动传递率函数；用主成分分析(Principal Component Analysis，PCA)提取结构损伤前后振动传递率函数的第一阶主成分作为正态总体样本；用多元统计分析中F 检验法进行假设检验分析以达损伤识别目的。该方法无需激励信息，具有一定抗噪声能力，适合处理激励未知、测量噪声等因素引起的不确定性问题。通过海洋平台结构数值模拟及振动台模型试验验证该方法的可行性。

关键词：损伤识别；传递率函数；主成分分析；海洋平台；假设检验

土木工程结构服役中会发生损伤，若不及时发现并采取有效措施，极有可能引起灾难性后果，造成巨大损失。因此，有必要对土木工程结构进行健康监测及损伤检测研究[1-2]。近20年来，基于振动的结构损伤检测法得到了快速发展[3-4]，不同程度解决了一些问题，而大多属于确定性方法。实际应用中，由于受激励未知、测量噪声及建模误差等因素引起的不确定性影响，确定性方法的损伤检测结果往往不够理想，故应考虑在损伤检测中引入处理不确定性问题的有效机制及方法。

统计推断作为处理不确定因素的有效方法，正尝试用于结构损伤识别领域[5-6]，主要包括参数估计与假设检验两部分。前者指根据从总体中抽取样本估计总体分布中包含的未知参数方法；后者又称显著性检验，基本思想即由样本推断总体间是否存在显著性差异，并用于土木工程结构的损伤识别。刘智[7]利用概率统计的假设检验方法研究基于ARMA模型系数及脉冲响应等钢结构损伤预警；林秀萍[8]利用模态参数研究基于概率统计的结构损伤识别；Sohn等[9]通过序贯概率比检验对8自由度结构损伤进行分类；Rizos等[10]结合假设检验与统计估计，对机翼蒙皮损伤及修复诊断进行研究；李炜明等[11]通过结构加速度响应对简单框架系统辨识进行假设检验分析从而对结构状态进行初步辨识；Mujica等[12]直接用加速度响应通过主成分分析及假设检验方法对简单钢板进行结构损伤识别研究。

基于统计假设检验的损伤识别方法考虑不确定性因素的影响，在简单结构损伤识别领域取得一定成就；但对较复杂的土木工程结构，统计量的选取仍受诸如风荷载、地震荷载等环境激励及测量噪声等因素影响。如何利用动力时程响应提取能反映结构运行状态的特征量成为统计模式识别的关键。为摆脱激励信息影响，Maia等[13]提出传递率函数概念，研究其对损伤的敏感性；Zhu等[14]在传递率函数理论基础上对门式钢架损伤位置进行准确判断；刁延松等[15]用传递率函数及神经网络成功对海洋平台结构进行损伤识别。这些研究均表明用传递率函数构造损伤指标的优越性。

本文利用振动传递率函数与统计假设检验进行结构损伤识别研究，即利用结构损伤前后加速度响应计算振动传递率函数，用PCA提取结构损伤前后振动传递率函数第一阶主成分作为正态总体样本，用多元统计分析的F 检验法构造统计量进行假设检验分析，以达到损伤识别目的。

1原理

1.1传递率函数

具有n自由度的振动系统微分方程为

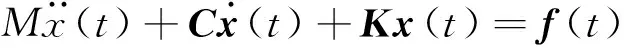
(1)

对式(1)进行傅里叶变换，得

X(ω)=H(ω)F(ω)

(2)

H(ω)=(K-ω2M+iωC)-1

(3)

式(3)为振动系统频响函数矩阵，n×n阶。

加速度列阵为

A(ω)=-ω2H(ω)F(ω)

(4)

设作用于结构k处单点激励为f(t)，并进行傅里叶变换，则激励列阵可写为

F(ω)={01,02,…,Fk(ω),…,0N}T

(5)

将式(5)代入式(4)，得

A(ω)=-ω2Fk(ω)Hk(ω)

(6)

式中：Hk(ω)为H(ω)的第k列。

设外部激励产生的加速度响应由i处向j处传递，定义加速度传递率函数为两处响应比值，即

从式(7)看出，传递率函数即为频响函数比值，该函数已摆脱对激励信息的依赖，且与该函数极点对应的是结构反共振频率，其对结构局部损伤更敏感[16]。因此，利用传递率函数进行结构损伤识别较直接用加速度响应更具优势。

1.2主成分分析

主成分分析(Principal Component Analysis,PCA)是将高维相关变量简化为少数几个不相关变量的多元统计分析方法[17-18]，在保证数据信息丢失最少前提下，经线性变换、舍弃部分信息，用少数变量代替原始数据信息，目前已用于结构损伤识别研究。

本文以振动传递率函数Kij为分析信号，并假设为平稳随机过程，将Kij分成n段，每段长度为p，组成p行n列矩阵T，将其每行减去自身均值后得H，设T的协方差矩阵为Σ，则有

(8)

对实对称矩阵Σ有

∑=UΛUT

(9)

式中：U=[u1u2…up]∈Rp×p为Σ的特征向量，且UUT=UTU=I，Λ为Σ的特征值λi(i=1,2,…,p)由大到小排列成的对角矩阵。该数据样本集的主成分为

(10)

式中：Pi为第i个主成分；μi为Σ的第i个特征向量，其中任意两主成分互不相关。且Pi方差为λi，由于λ1>λ2>…>λp>0，第一个主成分P1代表原始数据变异最大方向，且携带原始数据信息最多，P2次之，以此类推，则第i主成分贡献率为

(11)

式中:ψi值越大表明第i主成分综合数据T的能力越强。通常前几阶主成分均能含原始数据绝大部分信息，故仅分析前几阶主成分即能反映整个原始数据变化特征，则损伤识别可仅在前几阶主成分构成的低维空间中进行，因而能降低分析难度。

1.3多元统计的假设检验理论

损伤会引起结构物理参数变化，并体现于动力响应中，而由动力响应构造振动传递率函数的主成分也会相应发生变化，因此通过对比结构健康及测试状态振动传递率函数的主成分可判别结构损伤与否，从而进行结构损伤识别。

由于振动传递率函数主成分为多元变量，因此考虑用多元统计分析的均值向量检验对结构状态(损伤与否)进行判别。以振动传递率函数第一阶主成分作为正态总体样本，假设来自结构健康状态样本X(a)(a=1,2,…,m)服从N(μ1，Σ1) 正态分布，均值向量μ1及协方差阵Σ1未知；来自测试状态样本Y(a)(a=1,2,…,m)服从N(μ2，Σ2) 正态分布，均值向量μ2及协方差阵Σ2未知。两组样本相互独立，Σ1与Σ2不等且大于0，要求检验其是否来自相同的结构状态，取相同样本容量m。

由多元统计理论知识[19]，该问题可通过构造统计量进行假设检验，

令

X(a)=(Xa1,Xa2,…,Xan)T～Nn(μ1,Σ1)

(a=1,2,…,m)

Y(a)=(Ya1,Ya2,…,Yan)T～Nn(μ2,Σ2)

(a=1,2,…,m)

设H0∶μ1=μ2，H1∶μ1≠μ2

令

Zi=Xi-Yi,(i=1,2,…,m)

(12)

检验统计量为

(13)

本文取检验水平α=0.05，查F分布表使P{F>Fα}=α，可确定Fα值，再用样本值按式(13)求出F，若F>Fα，则否定H0，即两组样本来自不同状态，结构发生损伤；否则接受H0，结构完好。

1.4损伤识别步骤

用振动传递率函数及统计假设检验进行结构损伤识别研究，具体步骤为：①分别提取结构健康状态及待检测状态下加速度时程响应数据，按式(7)计算振动传递率函数，并分成m组；②将每组振动传递率函数分成n段，每段长度为p，组成p行n列矩阵H，按式(8)～式(10)进行主成分分析，取第一阶主成分(n维行向量)写成列向量并作为正态总体的一个样本，进而得不同状态下总样本矩阵X，Y；③查F分布表确定Fα值，按式(13)计算测试样本统计量F，若F>Fα，否定H0，即两组样本来自不同状态，结构发生损伤；否则接受H0，结构完好。

2数值模拟

2.1数值模型

用ANSYS10.0建立五层海洋平台的三维有限元模型，见图1。平台底层、顶层平面尺寸分别为0.7 m×0.5 m、0.4 m×0.3 m，层高0.5 m，横梁、柱及支撑均用Q235圆钢管，直径=8～12 mm。为模拟平台上部结构，在顶层设置0.65 m×0.55 m厚20 mm钢板，弹性模量选25℃时的1.932×1011N/m2，密度为7 800 kg/m3，泊松比μ=0.3，平台与基础固接。共模拟5种工况，分别为构件未损伤、构件①发生10%、30%、50%的损伤及构件①、②同时发生30%损伤，见表1。

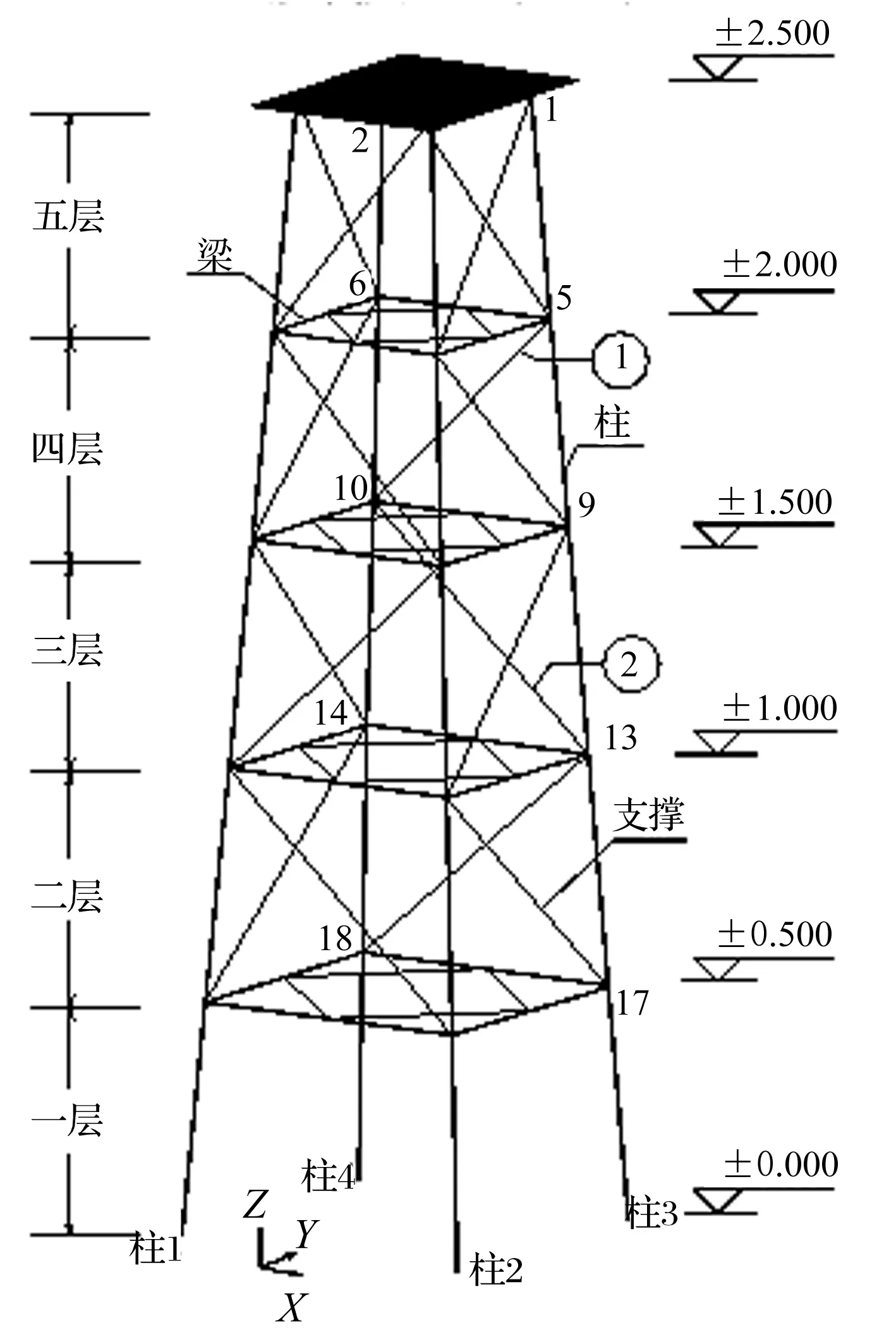
图1　数值模型Fig. 1 The numerical model

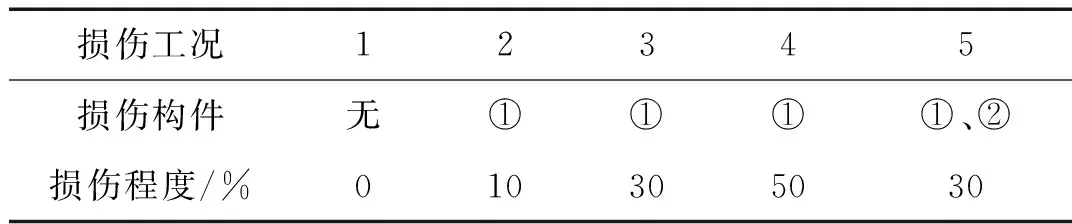
损伤工况12345损伤构件无①①①①、②损伤程度/%010305030

2.2白噪声激励下数值模拟

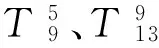
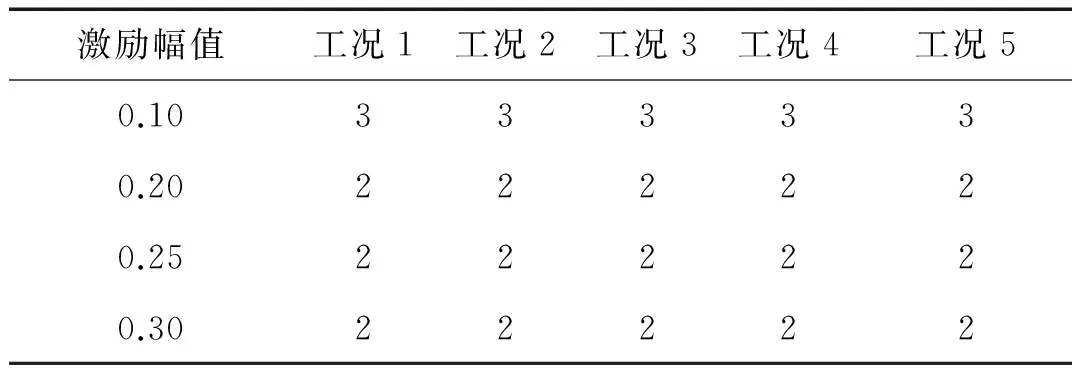
表2　不同幅值激励次数

以9、13点传递率函数为例，简述分析过程。用9次不同激励经计算获得9组长度10 000的数据，将每4 096个数据作为一次观测值，得样本容量为18。将每次观测值4 096个数据均分成8段长度为512的样本，组成512行8列矩阵，用主成分分析得不同工况下第一阶主成分特征值及贡献率见表3。

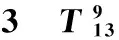
表 不同工况下第一阶主成分特征值及贡献率

由于第一阶主成分贡献率最大，包含原始数据信息量最大，因此选第一阶主成分作为正态总体样本，获得每种工况下样本为8×18矩阵，即样本容量m=18，维数n=8。递率函数T95的分析过程相同，由式(13)得不同工况下F值计算结果见表4。

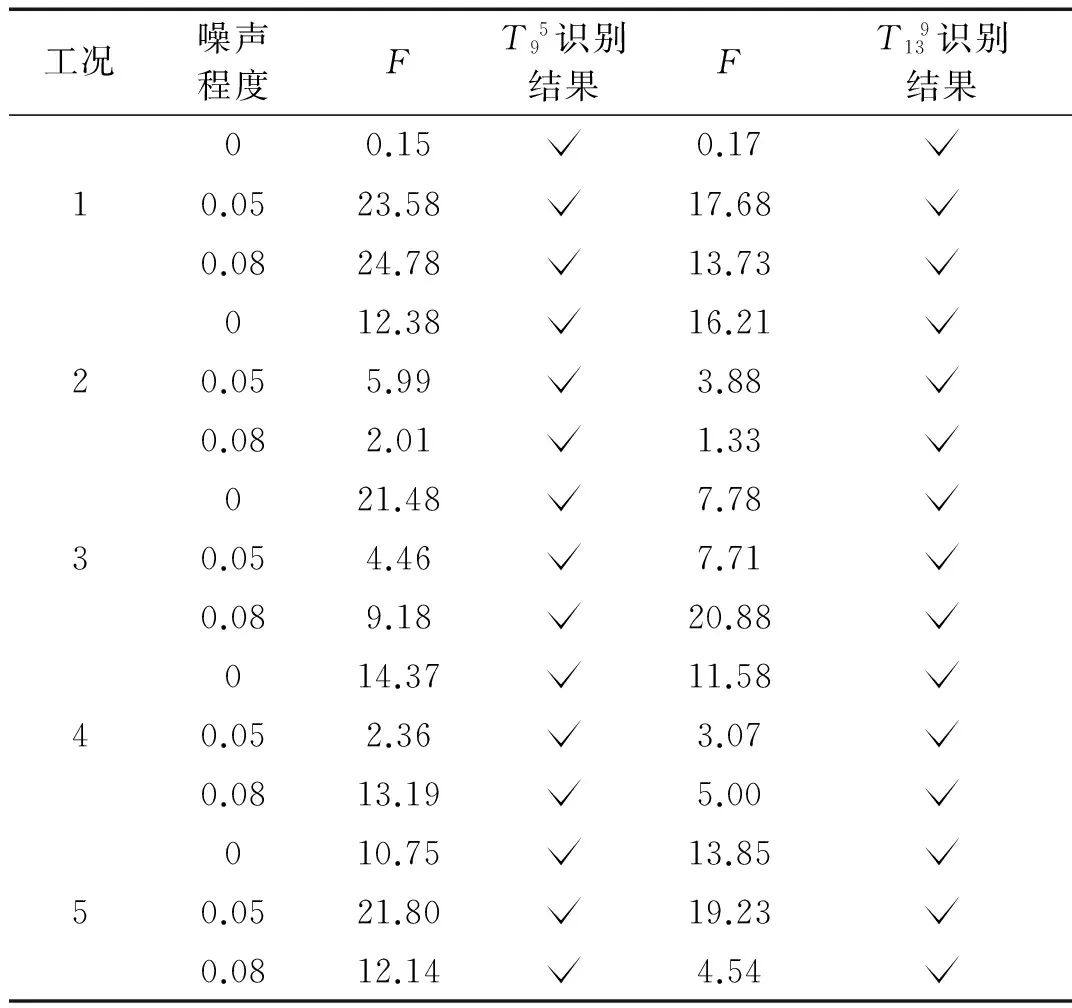
表4　不同噪声程度下的F值及识别结果

注：√表示识别正确，×表示识别错误

2.3测量噪声影响

实际应用中测量噪声不可避免，为考虑测量噪声影响，在加速度响应中叠加一定程度的正态分布随机白噪声，噪声模拟公式为

xnoise=x+RMS(x)NlevelNunit

(14)

式中：xnoise，x为有、无噪声的节点加速度响应；RMS(x)为无噪声加速度均方根；Nunit为均值=0、标准差=1的正态分布随机数据；Nlevel为所加噪声程度大小，本文取5%，8%，损伤识别结果见表4。

3试验验证

用白噪声激励的海洋平台结构损伤识别振动台模型试验数据，进一步验证方法的有效性。试验、数值模型的物理参数相同，试验仪器有：美国SILICON DESIGNS公司的Model 2220-005加速度传感器，量程5 g；德国Imc集成测控有限公司的CRONOS PL16-DCB8数据采集仪，40通道；北京东方振动与噪声技术研究所的INV-6多功能抗混滤波放大器，苏州试验仪器总厂的DY-1000-8电动振动台。台体激励为采样频率120 Hz白噪声，激励幅值为0.5、1、1.5。加速度响应采样频率为500 Hz。原支撑截面为12 mm×1.6 mm圆管，试验中用小截面替换件模拟损伤，实验设置见图2，损伤工况见表5。

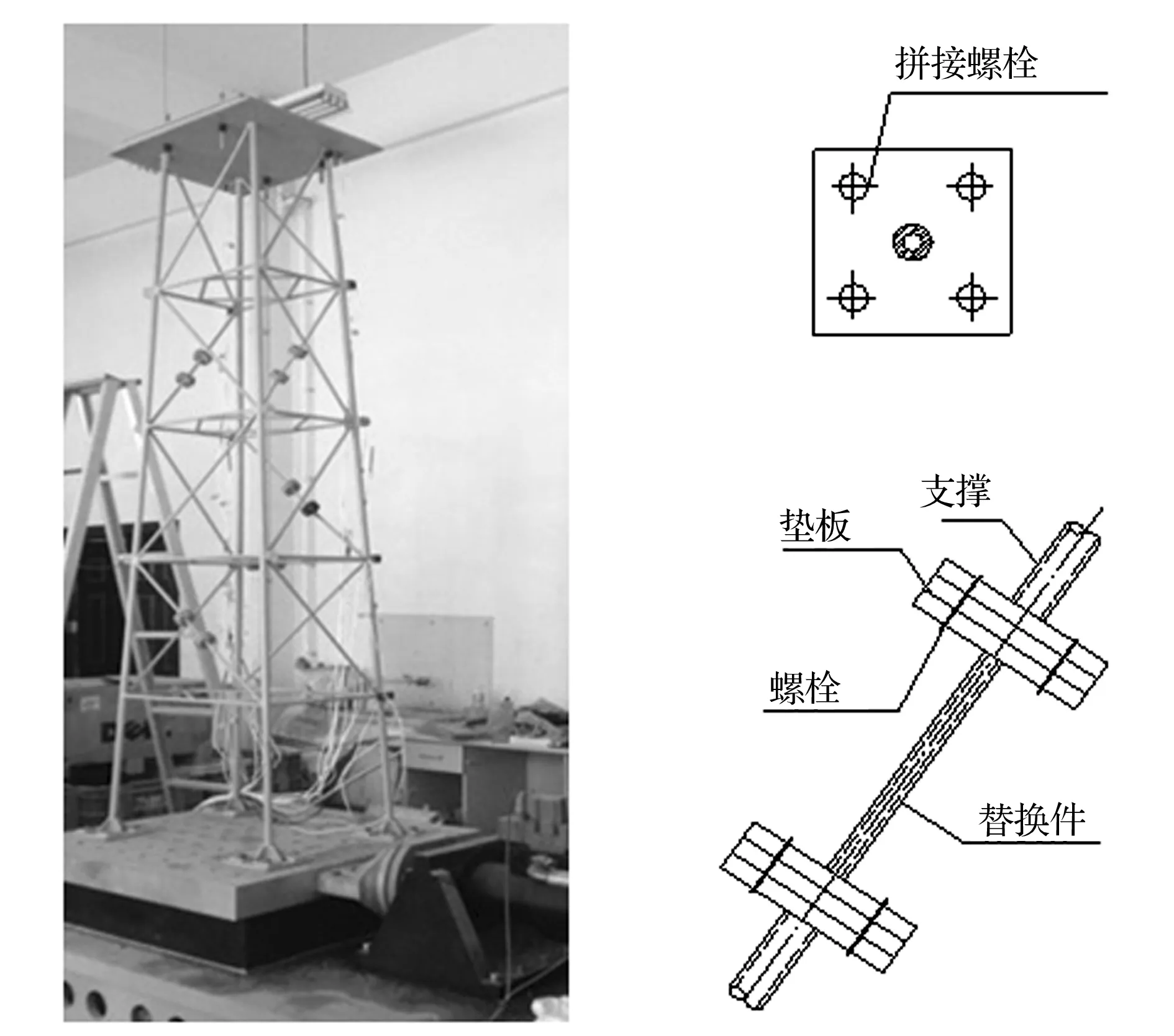
图2　试验设置及替换件大样Fig.2 The experiment setup and replacement parts details

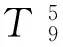
表5　模型试验的损伤工况

表6　模型试验F值及识别结果

注：√表示识别正确，×表示识别错误

4结论

利用振动传递率函数及统计假设检验进行结构损伤识别研究。该方法优点为，无需激励信息，具有一定抗噪声能力，适合处理激励未知、测量噪声等因素引起的不确定性问题。缺点为：需提取较多数据建立完备的基准样本集方可避免误判、漏判发生。需单点激励，对非单点激励的适用性有待研究。

参 考 文 献

[1] Wang M L, Heo G, Satpathi D. Health monitoring system for large structural systems[J]. Smart Material and Structures, 1998, 7(5):606-616.

[2] Aktan A E, Catbas F N, Grimmelsman K A, et al. Issues in infrastructure health monitoring for management[J]. Journal of EngineeringMechanics, 2000,126(7):711-724.

[3] Farrar C R, Worden K. An introduction to structural health monitoring[J]. Phil Trans R Soc, 2007，365(1861):303-315.

[4] 朱宏平,余璟,张俊兵. 结构损伤动力检测与健康监测研究现状与展望[J].工程力学,2011 (2):1-11.

ZHU Hong-ping, YU Jing, ZHANG Jun-bing.A summary review and advantages of vibration-based damage identification methods in structural health monitoring[J]. Engineering Mechanics, 2011(2):1-11.

[5] Farrar C R,Worden K. Structural health monitoring: a machine learning perspective[M]. New York: Wiley,2012.

[6] Farrar C R,Lieven N A J. Damage prognosis: the future of structural health monitoring[J]. Phil, Trans, R, Soc, 2007, 365(1851): 623-632.

[7] 刘智. 基于统计模式识别的空间钢结构损伤预警[D]. 哈尔滨:哈尔滨工业大学, 2010.

[8] 林秀萍. 基于概率统计方法的结构损伤识别研究[D]. 重庆:重庆大学, 2009.

[9] Sohn H, Worden K, Farrar C R. Statistical damage classification under changing Environmental and operational conditions[J]. Journal of Intelligent Material Systems and Structures, 2002, 13(9): 561-574.

[10] Rizos D D, Fassois S D, Marioli-Riga Z P, et al. Vibration-based skin damage statistical detection and restoration assessment in a stiffened aircraft panel[J]. Mechanical Systems and Signal Processing, 2008, 22(2): 315-337.

[11] 李炜明. 土木工程结构系统辨识的统计方法研究[D]. 武汉:华中科技大学, 2009.

[12] Mujica L E, Ruiz M, Pozo F, et al. A structural damage detection indicator based on principal component analysis and statistical hypothesis testing[J]. Smart Materials and Structures,2014, 23 (2) : 14-25.

[13] Maia N M M,Silva J M M, Ribeiro A M R. The transmissibility concept in multiple degrees of freedom systems[J]. Mechanical Systems and Signal Processing, 2001, 15(1):129-137.

[14] Zhu D P, Yi X H, Wang Y, et al. Mobile sensor networks: a new approach for structural health monitoring[C]//Structures Congress 19th Analysis and Computation Specialty Conference. Orlands Florida, 2010:159-168.

[15] 刁延松,张启亮,孟冬梅.基于振动传递率的钢质导管架海洋平台结构损伤识别方法研究[J].建筑钢结构进展,2013, 15(1):50-56.

DIAO Yan-song, ZHANG Qi-liang, MENG Dong-mei. Study on the damage identification methon of steel jacket offshore platform based on vibration transmissibility function[J]. Progress in Steel Building Structures, 2013, 15(1):50-56.

[16] Steenackers G, Devriendt C, Guillaume P. On the use of transmissibility measurements for finite element model updating[J]. Journal of Sound and Vibration, 2007, 303:707-722.

[17] 陈志为. 基于统计模式识别技术的结构异常检验[D]. 福州:福州大学, 2005.

[18] 于秀林,任雪松.多元统计分析[M]. 北京:中国统计出版社, 2011.

[19] 朱建平. 应用多元统计分析[M]. 北京:科学出版社, 2012.

基金项目：国家自然科学基金(51179082)；山东省蓝色经济区工程建设与安全协同创新中心

收稿日期：2015-03-30修改稿收到日期：2015-06-11

中图分类号:TU312.3

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.02.037

Structural damage identification of offshore platform based on the vibrationtransmissibility function and statistical hypothesis testing

DIAO Yan-song1,2， XU Dong-feng1, XU Jing1,2， MAO Hui1,2

(1. School of Civil Engineering, Qingdao Technological University, Qingdao 266033, China;2. Collaborative Innovation Center of Engineering Construction and Safety in Shandong Blue Economic Zone, Qingdao 266033, China)

Abstract:The results of the structural damage identification based on vibration have obvious uncertainty because of the influences of unknown excitation, measurement noise and modeling error. Here, the vibration transmissibility function and statistical hypothesis testing methods were utilized to identify the structural damage. Firstly, the acceleration responses before and after the structural damage were used to calculate the vibration transmissibility function. Then the first principal component of vibration transmissibility function before and after the structural damage was extracted with principal component analysis (PCA), which was treated as a sample of normal population. Finally, the F-test of multivariate statistical analysis was employed for hypothesis testing analysis to achieve the purpose of damage identification. This method does not need information of excitation and is able to resist noise, it’s suitable for handling uncertain problems resulting from unknown excitation and measurement noise. The numerical simulation of an offshore platform structure and the shaking table model test showed that the proposed method is feasible.

Key words:damage identification; transmissibility function; principal component analysis(PCA); offshore platform; hypothesis testing

第一作者 刁延松 男，博士，教授，1968年8月生