船用高速发电机基波磁场下机座电磁振动

张贤彪， 王　东， 顾太平， 刘德志

(海军工程大学 舰船综合电力技术国防科技重点实验室，武汉　430033)



船用高速发电机基波磁场下机座电磁振动

张贤彪， 王东， 顾太平， 刘德志

(海军工程大学 舰船综合电力技术国防科技重点实验室，武汉430033)

摘要：以船用高速同步发电机为对象进行电磁振动特性分析。用有限元法计算空载下电机基波气隙磁场引起的径向电磁力波在机座机脚处垂向振动加速度。通过对不同机座安装方式、材料刚度及结构阻尼的振动仿真对比，分析影响振动加速度主因及有限元模型简化处理对计算结果影响。用三维谐波场及瞬态场有限元法计算机脚振动加速度，用电动机运行法测试发电机空载下机座机脚振动加速度。结果表明，仿真与试验结果基本一致，机座及机脚振动受机座安装方式影响较大，定子振幅受材料弹性模量响应较大，在弹性安装/自由状态下机座形变分布主要受结构阻尼影响。该结果可为船用高速电机减振降噪设计、研究提供依据及参考。

关键词：电磁振动；基波磁场；船用发电机；有限元法

由于对船舶声隐身性能要求提高，振动、噪声已成为衡量船用发电机的主要技术指标之一。电机振动按产生机理可分为电磁、机械及空气动力三类[1]。其中，电磁振动主要为气隙磁场引起电磁力振动(暂不考虑磁致伸缩引起的振动[2-3]及定子端部磁场引起的绕组振动[4])，作为电机的寄生效应[5]广受关注。电磁力按气隙磁场作用方向可分为径向、切向及轴向力，径向力中一般考虑基波磁场产生的倍频力波及由定转子谐波磁场相互作用产生的径向力波，为电磁振动主要激励源。各径向力波作用于定转子铁心，使定子铁心、机座及转子出现随时间周期性变化的径向形变(振幅)。

目前对各类电机电磁振动研究多针对定子铁心及机座。对振动激励源及传递途径，通过分析径向电磁力波模型及机座结构模态，可揭示气隙长度、槽配合、转子槽形等主要电磁参数对电磁力波影响规律及结构固有振动特性。以电磁力波避开结构固有频率及模态阶次为主要原则，整体优化电机电磁、结构参数实现电机低电磁振动[6-12]。对振动响应，由于气隙电磁场与定子振动为弱耦合关系[13-14]，主要采用电磁场、应力场相结合的有限元法[15]；据电机实际安装方式及分析方便，计算工况多为电机空载运行，且机座与基础之间为刚性约束或自由状态[16]。

由于基波磁场产生的倍频力波存在阶次低、幅值大且难以削弱等特点，是电磁振动激励源的主要分量。实现船用高速发电机低电磁振动优化设计，需分析基波磁场产生的倍频力波振动。为此，本文以船用高速同步发电机为对象，用机脚振动加速度参数作为振动响应表征，采用磁场、应力场相结合的有限元法计算空载下电机基波气隙磁场产生的倍频力波振动。通过对不同机座安装方式、材料刚度及结构阻尼的振动仿真对比，分析影响振动加速度主因及有限元模型简化对计算结果影响，在此基础上分别采用三维谐波场及瞬态场有限元法计算机脚振动加速度，并实验验证。

1电磁振动数学模型

1.1电磁振动响应模型

多自由度系统由弹性恢复力、阻尼力、惯性力及电磁激振力形成的平衡系统，据达朗贝尔原理得运动方程为

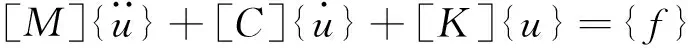
(1)

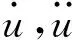
运动方程在模态坐标系下分解为n个独立方程，令{u}=[s]{η}，则有

(2)

电机气隙基波磁密为B(θ,t)=B0cos(pθ-wet)。其中B0为基波磁密幅值；p为电机极对数；θ为定子圆周相位；we为电频率。作用于定子铁心内表面单位面积的径向磁拉力正比于磁通密度平方，即：f(θ,t)=B2(θ,t)/(2μ0)，其中μ0为气隙长度。不考虑常数项，得倍频力波为

f(θ,t)=f0cos(2wet-2pθ)

(3)

据式(3)，设{f}=(f0)cos(2wet)，则{h}=[s]T[M]-1(f0)cos(2wet)={H0}cos(2wet)，代入式(2)求解得稳态电磁振动响应为

(4)

式中：H0i为模态坐标下第i阶广义电磁力波幅值；φi为模态坐标下第i阶节点位移向量相位。

已知{u}=[s]{η}，代入式(4)得

(5)

式中：s(i)为坐标系变换矩阵第i阶元素。

由式(5)可知，振动响应幅度与电磁力波幅值H0i成正比，阻尼比ξi越大振幅ui越小，并与电频率we及模态频率wi密切相关。以定子电磁振动为例，倍频力波频率与定子模态频率相等且阶次相同时(wi=2we,i=2p)，电机定子振幅最大。

1.2定子结构模型

结构固有频率随刚度增大而增大，随质量增大而减小。对形状及尺寸一定的均匀材料结构，增加材料弹性模量或减小材料密度能提高固有频率，反之则降低。定子绕组由多匝电磁线经绝缘包扎、浸漆处理后形成，与实心导电用铜结构不同，其弹性模量远小于实心结构(E=1.08×1011N/m2)，但质量与实心结构相当。有限元建模中，绕组多被作为附加质量计入铁心或铁心磁极[17]。而对较大型定子结构，有效部分绕组对固有频率影响较大，不能简单以附加质量形式计算[18]。故分析绕组对振动影响时忽略端部结构，有效部分按均匀实体建模，选不同弹性模量进行计算。

定子铁心由硅钢片叠压而成，与实心结构不同。在各向异性模型中有一各向同性面(径向平面xoy)，z向为叠压方向，其弹性模量Ez相对较低。定子铁心材料参数模型为

(6)

式中：Er，vr，Gxy为径向弹性模量、泊松比及剪切模量。参数值由硅钢材料决定；Ez与叠压工艺有关，须通过试验测试。铁心弹性模量一般取Er=2.0×1011N/m2，Ez=1.5×1011N/m2。

为分析定子铁心对振动影响，分别按各向同性、异性对比计算。

1.3机座结构模型

船用发电机座通过隔振器安装在基础上，为弹性安装。有限元建模中忽略隔振器质量只计其连接刚度，采用弹性模拟。据隔振器隔振频率fL及额定载荷ML计算垂向连接刚度为

KL=ML(2πfL)2

(7)

连接刚度越大机座固有频率越高。为分析安装方式对振动影响，对比计算机座自由状态、刚性及弹性安装三种方式的振动响应。机座主要为普通钢结构，阻尼比ξ一般直接按经验值0.02计算，或分解为质量阻尼及刚度阻尼系数后计算，即

(8)

式中：α，β为质量、刚度阻尼系数，经验值分别取3.0及0.0001。为分析结构阻尼对振动影响，对比计算有、无阻尼振动响应。

2三维有限元模型及分析

船用发电机系统结构主要包括电机定子、机座(隔板、底板、侧板、机脚)、转子与端盖式轴承及定子以上部件(整流装置、励磁装置、风机等)。定子及机座见图1，其中1为定子，2为侧板，3为机脚，4为底板，5为隔板。

图1　定子及机座三维虚拟样机图Fig.1 Structure of stator core and frame

为便于有限元建模，对定子及机座作常规简化：① 忽略定子通风槽、绕组端部等结构对计算影响，将其简化为圆筒；绕组与铁心固连，铁心与隔板固连。② 忽略结构焊接部分，将隔板、侧板、底板各部分视为固连。③ 忽略对计算影响不大的孔、槽及倒角等。整机采用体单元SOLID186，定子模型采用六面体网格划分。该发电机极对数为2。空载、额定转速下定子径向电磁力波作用在定子内表面，有限元模型见图2。

图2　定子及机座有限元模型Fig.2 Finite element model of stator core and frame

分别采用三维谐波场、瞬态场有限元法计算机脚处4个振动测点的平均加速度。瞬态场分析采用Full完全法，选加载时间为5个周期，每周期分40个载荷步。为获得稳定振动，只分析最后一个周期数据结果。

3振动特性分析

3.1机座自由状态下振动影响因素分析

3.1.1定子、机座形变

机座为自由状态时机脚无自由度约束。定子分两种处理情况：① 低模量：绕组按均匀实体铜建模，不考虑弹性模量，铁心叠压结构按各向异性建模，径向弹性模量取2.0×1011N/m2，叠加方向取1.5×1011N/m2。② 高模量：绕组按均匀实体铜建模，弹性模量取1.08×1011N/m2；铁心叠压结构按各向同性建模，弹性模量取2.0×1011N/m2。机构结构阻尼处理为有阻尼时阻尼比取0.02，无阻尼时阻尼比取0。定子为低模量下机座形变见图3。由图3可知，有结构阻尼机座最大形变主要集中在侧板上半部及尾部隔板处；无结构阻尼机座最大形变量主要集中在侧板、底板头部。有结构阻尼时定子形变见图4。

图3　机座自由状态形变云图Fig.3 Deformation distribution of frame in free installation

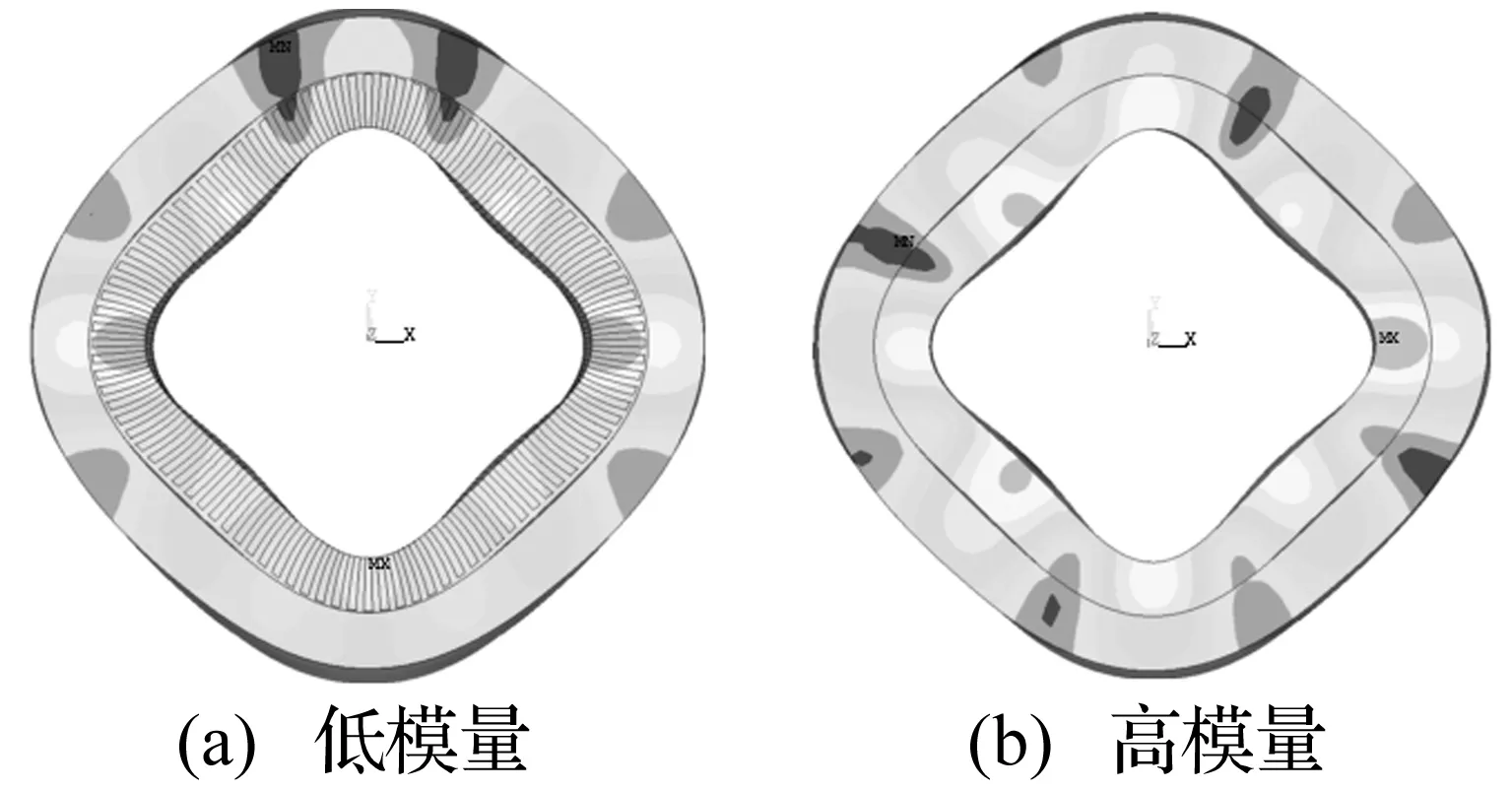
图4　机座自由状态下的定子形变云图Fig.4 Deformation distribution of stator core with free installed frame

机座自由状态下定子、机座形变见表1。由表1知，有、无结构阻尼下定子最大形变值基本相同。无阻尼下机座最大形变量较大，主要分布在机座头部；相反，有阻尼的机座最大形变量较小，且主要分布在机座尾部。机座及定子最大形变量随材料弹性模量增大而减小。因此，对自由状态，机座最大形变量及分布主要受阻尼影响，而最大形变量随阻尼及定子材料的弹性模量增大而减小。定子最大形变量主要受材料弹性模量影响。

表1　自由状态下的定子及机座形变

3.1.2机脚垂向加速度

自由状态下机脚振动加速度见表2。由表2知，较结构阻尼的机脚垂向振动，有结构阻尼最大加速度值较小，平均加速度值较大。定子为高模量时加速度小于低模量。由此得机座自由状态的机脚垂向平均加速度级为111～112 dB。

表2　自由状态下机脚垂向振动加速度

3.2机座刚性安装的振动影响因素分析

3.2.1定子、机座形变

机座刚性安装时，将机脚与隔振器螺栓连接视为与基础固连，约束垂向位移为0。定子低模量下机座形变见图5。由图5知，有、无结构阻尼的机座最大形变量及分布基本一致，形变主要集中在机座中部及头部底板。

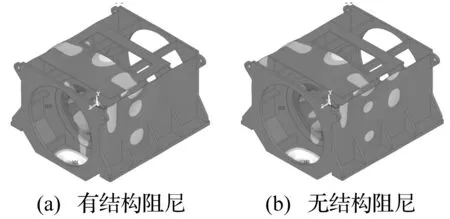
图5　机座刚性安装的形变云图Fig.5 Deformation distribution of frame in fixed installation

刚性安装的定子、机座形变见表3。由表3看出，刚性安装时机座、定子形变量及分布稳定，受结构阻尼及材料弹性模量影响较小。

表3　刚性安装定子、机座形变

3.2.2机脚垂向振动加速度

刚性安装的机脚振动加速度见表4。由表4可知，此时振动加速度受结构阻尼影响可忽略；定子为高模量时机脚振动加速度略小于低模量。

表4　刚性安装机脚垂向振动加速度

3.3机座弹性安装的振动影响因素分析

机座弹性安装时隔振器按弹簧单元建模。据计算结果分析知，此时形变及机脚振动加速度与自由状态的值基本一致。定子为低模量的机座形变见图6。

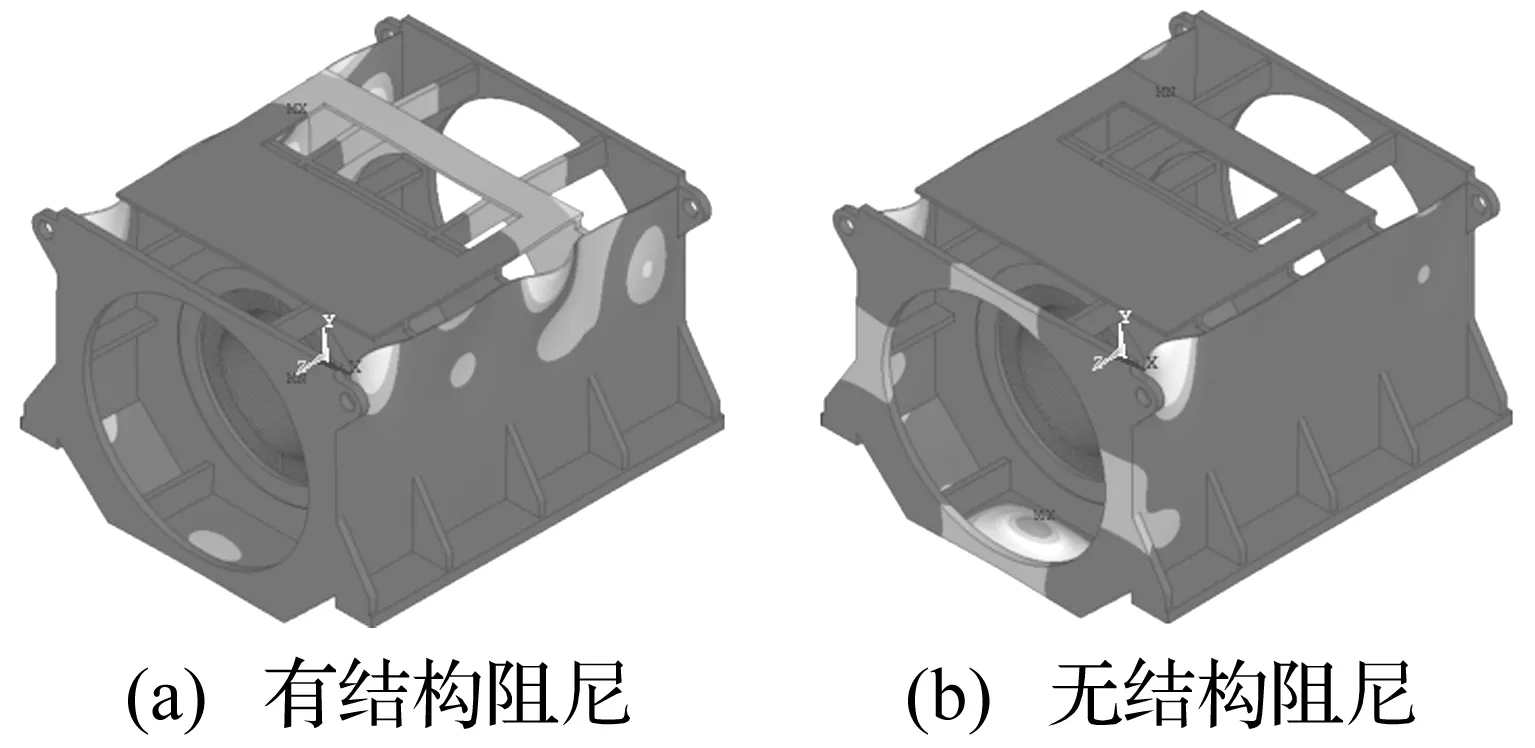
图6　弹性安装的机座形变云图Fig.6 Deformation distribution of frame in flexible installation

弹性安装时机脚振动加速度见表5。

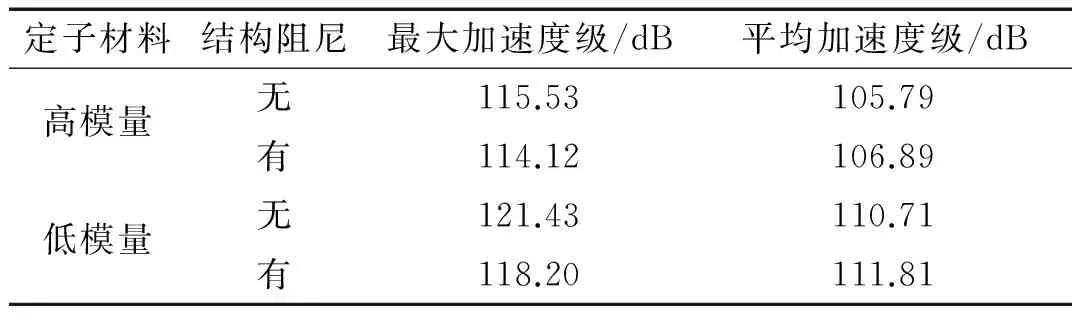
表5　弹性安装机脚垂向加速度

3.4振动特性分析

据机座不同安装方式的振动影响因素分析知，① 机座形变主要受安装方式影响，安装刚度越大机座形变量越小。刚性安装时机座形变基本不受结构阻尼及定子材料弹性模量影响；弹性安装或自由状态时形变分布主要受结构阻尼影响，形变量随阻尼及弹性模量增大而减小。② 定子形变量主要受弹性模量影响，其次为机座安装方式，基本不受结构阻尼影响。弹性模量越高或机座安装刚度越大定子最大形变量越小。③ 机脚垂向加速度受机座安装方式影响最大，其次为材料弹性模量，基本不受结构阻尼影响。安装刚度或弹性模量越大振动越小。刚性安装的弹性模量对振动影响相较弹性安装小，因安装方式影响占主导。④ 已知电机弹性安装，机脚加速度分布式测量，取平均加速度值作为测试结果。定子绕组实际结构中因绝缘、槽楔等其弹性模量较低，绕组按均匀实体铜建模可不计弹性模量；铁心叠压结构应按各向异性建模，因此机座弹性安装且定子低模量时机脚振动平均值加速度更符合电机实际安装及定子铁心结构。仿真计算值为111～112 dB。

4实验验证及分析

电磁振动实验中，为避免轴系耦合对振动测量的影响，将发电机作为同步电动机空载运行，通过三相变频器拖动至额定转速。机座通过4个隔振器与试验底板连接，振动测点布置在机座与减振器的连接螺栓处，测量机脚垂向加速度。电磁振动测试方案见图7。图中，1为振动测点，2为隔振器，3为试验底板。

图7　电磁振动测试方案Fig.7 Test scheme of electromagnetic vibration

采用同一电机定子、机座，分别装配3种不同结构轴承进行振动测试。4个测点主要倍频(对转频而言)振动分量见表6。据电机轴承转速、载荷及稳定性要求等选择可倾瓦轴承，常用结构形式有4片、5片瓦两种。表6中A为4片瓦轴承；B、C为5片瓦轴承。据上、下侧瓦片数不同分别为上侧两片、下侧三片及上侧三片、下侧两片。基波磁场产生的倍频力波为电频率的2倍、转频的4倍。由表6知， 4倍转频平均垂向加速度为0.51～ 0.99 m/s2，转换成分贝为114.2～119.9 dB。仿真结果为111～112 dB，与实测值基本一致，相对误差为2%～7%。仿真误差主要源于有限元求解及模型简化处理。

表6　主要倍频振动分量

为排除有限元求解误差，对比三维谐波场及瞬态场有限元法，所求机脚垂向加速度相对误差见表7。由表7知，用两种方法计算的差值较小，相对误差在3%以内，由此知，有限元求解误差较小。在有限元模型常规简化中，由于忽略过盈装配连接及焊接部分，将机座、定子铁心及绕组视为整体，使整个结构刚性增加，造成计算结果偏小。铁心叠片结构取各向异性，径向弹性模量按经验取值2.0×1011N/m2，该值偏大而使计算结果偏小。

表7　加速度相对误差

5结论

通过对船用高速发电机基波磁场下机座电磁振动特性有限元仿真分析，结论如下：

(1) 机脚垂向加速度受机座安装方式影响最大，定子材料弹性模量次之，结构阻尼无影响。机座安装刚度或定子弹性模量越大振动越小。

(2) 机座电磁振幅(形变量)及分布主要受机座安装方式影响。刚性安装时机座形变基本不受结构阻尼及弹性模量影响；弹性安装或自由状态时形变分布主要受结构阻尼影响，形变量随结构阻尼及材料弹性模量增大而减小。

(3) 定子形变量主要受弹性模量影响，其次为机座安装方式，结构阻尼无影响。弹性模量越高或机座安装刚度越大定子最大形变量越小。

(4) 机脚垂向加速度仿真值与实测值基本一致，相对误差为2%～7%；有限元求解误差较小，用两种有限元求解的机脚垂向加速度级相对误差在3%以内；有限元建模中对各结构简化处理会导致仿真误差。

参 考 文 献

[1] Lisner R P, Timar P L. A new approach to electric motor acoustic noise standards and test Proeedures [J]. IEEE Transactions on Energy Conversion,1999,14(3):692-697.

[2] 郝清亮,胡义军,朱少林. 磁致伸缩在电机电磁振动中的贡献分析[J]. 电机与控制应用,2011, 38(10):31-35.

HAO Qing-liang, HU Yi-jun,ZHU Shao-lin. Contribution analysis of magnetostriction in motor electromagnetic vibration [J]. Electric Machines & Control Application, 2011,38(10): 31-35.

[3] Delaere K, Heylen W, Belmans R,et al. Comparison of induction machine stator vibration spectra induced by reluctance forces and magnetostriction[J]. Magnetics, IEEE Transactions on, 2002, 38(2): 969-972.

[4] 鲍晓华,方勇,程晓巍,等.大型充水式潜水电机定子端部绕组电磁振动研究[J].电工技术学报,2013, 28(11):138-146.

BAO Xiao-hua, FANG Yong, CHENG Xiao-wei, et al. Research on electromagnetic vibration of stator end winding of large water filling submersible motor [J]. Transactions of China Electrotechnical Society, 2013, 28(11): 138-146.

[5] 杨浩东.永磁同步电机电磁振动分析[D].杭州：浙江大学,2011.

[6] Sakamoto S，Hirata T． Vibration analysis considering higher harmonics of electromagnetic forces for rotating electricmachines[J]． IEEE Transactions on Magnetics，1999, 35(3): 1662-1665．

[7] Schlensok C, Schmülling B, van der Giet M, et al. Electromagnetically excited andible noise-evaluation and optimization of electrical machines by numerical simulation[J]. COMPEL: The International Journal for Computation and Mathematics inElectrical and Electronic Engineering, 2007,26(3): 727-742．

[8] Dai Ying, Cui Shu-mei, Zhang Qian-fan. Analysis on electromagnetic vibration/noise of induction motors for EV drives [J]. Proceedings of the CSEE, 2012, 33(32): 89-97.

[9] 张磊,温旭辉.车用永磁同步电机径向电磁振动特性[J].电机与控制学报,2012,16(5):33-39.

ZHANG Lei, WEN Xu-hui. Radial electromagnetic vibration model characteristics of PMSMs for electric vehicles[J]. Electric Machines and Control, 2012, 16(5): 33-39.

[10] 钟焱,丁妍,冯海军,等.异步电动机电磁振动试验研究[J].噪声与振动控制,2011,5:165-167.

ZHONG Yan, DING Yan, FENG Hai-jun,et al. Experimental study on electromagnetic vibration of asynchronous motor [J].Noise and Vibration Control, 2011, 5:165-167.

[11] 杨浩东,陈阳生.分数槽永磁同步电机电磁振动的分析与抑制[J].中国电机工程学报,2011,24(31):83-89.

YANG Hao-dong, CHEN Yang-sheng. Electromagnetic vibration analysis and suppression ofpermanent magnet synchronous motor with fractional slot combination[J]. Proceedings of the CSEE, 2011, 24(31): 83-89.

[12] 左曙光,林福,孙庆,等. 极槽配合和绕组层数对永磁同步电机振动的影响分析[J].振动与冲击,2014,33(13):130-134.

ZUO Shu-guang, LIN Fu, SUN Qing, et al. Vibration of permanent magnet synchronous motor with different slot-pole combinations and winding layers[J].Journal of Vibration and Shock,2014,33(13):130-134.

[13] Rainer S, Biro O, Weilharter B, et al. Weak coupling between electromagnetic and structural models for electrical machines [J]. Magnetics, IEEE Transactions, 2010,46(8): 2807-2810.

[14] Lee J H, Lee Y H, Kim D H,et al.Dynamic vibration analysis of switched reluctance motor using magnetic charge force density and mechanical analysis[J]. Applied Superconductivity, IEEE Transactions, 2002, 12(1): 1511-1514.

[15] 王玎,祝长生,符嘉靖.基于有限元的异步电机电磁振动分析[J].振动与冲击, 2012, 31(2):140-144.

WANG Ding, ZHU Chang-sheng, FU Jia-jing. Electromagnetically excited vibration analysis for an asynchronous electrical machine with finite element method[J]. Journal of Vibration and Shock, 2012, 31(2): 140-144.

[16] 韦春健,刘德志,王东.空载情况下三相异步电动机径向电磁振动特性[J].电机与控制应用,2010, 37(12):13-17.

WEI Chun-jian, LIU De-zhi, WANG Dong. Three-phase asynchronous motor radial electromagnetic vibration analysis without loads[J]. Electric Machines & Control Application, 2010, 37(12): 13-18.

[17] 吴建华. 基于物理模型开关磁阻电机定子模态和固有频率的研究[J]. 中国电机工程学报, 2004, 24(8): 110-114.

WU Jian-hua. Study on the stator mode shapes and resonant frequencies of switched reluctance motor based on real structural model[J]. Proceedings of the CSEE, 2004, 24(8): 110-114.

[18] 王天煜, 王凤翔. 大型异步电动机定子振动与模态分析[J]. 中国电机工程学报, 2007, 27(12): 41-45.

WANG Tian-yu, WANG Feng-xiang. Vibration and modal analysis of stator of large induction motors[J]. Proceedings of the CSEE, 2007, 27(12):41-45.

基金项目：国家自然科学重点基础研究发展计划973项目(2013CB035601);国家自然科学基金资助项目(51137005,51222705)

收稿日期：2014-09-18修改稿收到日期：2014-11-06

通信作者王东 男，博士，教授，博士生导师，1978年生

中图分类号:TH113

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.02.033

Electromagnetic vibration characteristics of marine high-speed generator framederived from fundamental magnetic field

ZHANG Xian-biao, WANG Dong, GU Tai-ping, LIU De-zhi

(National Key Laboratory for Vessel Integrated Power System Technology,Naval University of Engineering, Wuhan 430033, China)

Abstract:With the increase of speed and power-density, the vibration problem of marine high-speed generator has become much more severe. Aiming at this problem, the vertical vibration acceleration at the machine feet of a marine high-speed synchronous generator was studied by finite element method (FEM), which is derived from the radial electromagnetic force due to the fundamental air-gap magnetic field in no-load condition. The vibration characteristicsis were analysed under different type of frame installations, different material stiffness and different structural damping. The main influential factors were classified clearly by comparative analysis. Moreover, the simplification of finite element model was introduced. The vibration acceleration at the machine feet was calculated by using the three dimensional harmonic field FEM and the transient field FEM respectively. The tested vertical vibration acceleration at machine feet of marine high-speed synchronous generator when running as a no-load motor was presented. The simulation results were compared with the test results, where a substantial agreement was achieved. The results show that frame and feet’s vibrations are impacted by installations greatly and the material stiffness is the main influential factor of stator’s vibration amplitude. Moreover, the frame’s damping has a significant effect on the vibration amplitude distribution under free or flexible installation. The results provide a theoretical reference to the analysis of marine high-speed generator vibration and noise reduction.

Key words:electromagnetic vibration; fundamental magnetic field; marine generator; finite element method

第一作者 张贤彪 男，博士生，1986年10月生