基于损伤累积的爆破振动传播规律试验研究

褚怀保， 叶红宇， 杨小林， 梁为民， 余永强

(河南理工大学 土木工程学院，河南　焦作　454000)



基于损伤累积的爆破振动传播规律试验研究

褚怀保， 叶红宇， 杨小林， 梁为民， 余永强

(河南理工大学 土木工程学院，河南焦作454000)

摘要：为进一步揭示基于损伤累积的爆破振动波传播与衰减规律，设计混凝土试块进行损伤累积及爆破振动测试试验。结果表明，测点损伤值随爆破次数增加持续增大，中远区测点损伤有初期缓增及后期突增两阶段；测点单次爆破振动速度随距离增大而减小，近区测点振动速度减小较中、远区测点快；测点爆破振动速度随爆破次数增加总体减小，且爆源近区减小较快，中远区呈小幅度缓慢减小；随爆破次数继续增大各测点振动速度存有突增过程，且衰减系数α增加缓慢，K值减小，两者均存在小幅度畸变过程；多次爆破时确定振动安全阈值及爆破振动波传播衰减规律(K、α值)时应充分考虑损伤累积效应。

关键词：损伤累积；爆破振动；传播与衰减规律；试验研究

爆破技术广泛用于矿山开采、隧道开挖、铁路公路路堑开挖、各类建(构)筑物基础开挖与处理、水利水电设施建设及核电建设工程等领域，可加快工程建设速度、提高生产效率，经济、社会效益显著[1]。随爆破规模、次数增大增多，所致危害效应随之增大，尤其爆破地震效应，不可避免对周围混凝土类建(构)筑物结构(如混凝土衬砌、混凝土大坝、各类混凝土基础等)造成一定程度扰动损伤及破坏[2-5]，严重影响其强度及耐久性，威胁结构的稳定性。因此，爆破振动危害评价与控制成为爆破安全技术的重大研究课题[6]。

对爆破振动危害评价、控制的依据为《爆破安全规程》(GB6722-2003)，该规程建立在大量结构爆破振动危害的调查统计基础上。而该评价方法及控制指标只考虑爆破振动质点峰值速度及主频，且均基于单次爆破，未考虑对混凝土结构塑性损伤的累积效应，对周边环境影响不可避免，甚至引发纠纷。

本文设计混凝土试块损伤累积进行表面爆破的振动及超声波测试，揭示基于损伤累积效应的振动传播与衰减规律，以期为科学的安全判据构建、灾害控制研究提供参考，提升混凝土耐久性，延长工程寿命，确保混凝土结构在不同爆破振动环境的可靠性。

1爆破振动形成机理

孔或药室内炸药爆炸会产生高温高压爆轰气体膨胀挤压周围介质，在介质中产生冲击波或应力波，冲击波使药包近区介质发生粉碎性破坏而消耗大量能量并迅速衰减为应力波。应力波携带能量继续传播使介质承受剪切及拉应力，在介质内产生新的裂隙或促使原裂隙进一步扩展，衰减的应力波携带剩余能量传播到地面形成周期性震动的地震波引起地面质点振动。冲击波与应力波在介质中的传播会改变介质内部应力场并劣化力学性质。

炸药爆炸引起的地面质点振动非常复杂，爆破条件、类型、爆区地形、地质条件及传播介质特性等诸多因素均对振动效果及衰减特性产生影响，其振幅、周期及频率均随时间、空间变化，振动物理量一般用质点振速、加速度、位移及频率等表示，即用地面质点振动速度作为爆破地震效应强度的衡量指标，爆破振动衰减规律理论依据多采用萨道夫斯基经验公式[7]，即

V=K(Q1/3/R)α=Kρα

(1)

式中：V为质点振动速度(cm/s)；Q为装药量(kg)；R为测点至爆破中心距离(m)；K，α为与爆源至测点间地形、地质条件有关的系数及衰减指数；ρ=Q1/3/R为比例药量。

K，α通过爆破试验所得介质质点振动速度及相应药量、距离实测数据，利用最小二乘法求解获得。将式(1)两边取对数，得

lnV=lnK+αlnρ

(2)

设y=lnV,a=α，x=lnρ，b=lnK，据最小二乘法原理及二元函数极值定理得

(3)

由式(3)求得a，b唯一解，再由变量代换，得

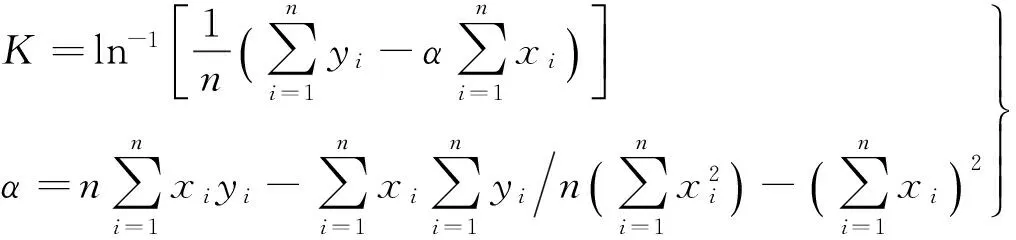
2混凝土试块爆破损伤累积试验方法

在实验室制作C40混凝土试块，尺寸为1 500 mm×500 mm×300 mm，见图1(a)。机械搅拌后在模板中用小型振动棒振捣成形，人工养护28天。在距试块一端300 mm处预留炮孔，深度180 mm，直径16 mm，试验时装入3.5 g黑索金炸药，湿润黄土堵塞，引火药头引爆。

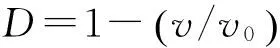
图1　试验图片Fig.1 Experimental pictures

3混凝土试块爆破试验结果及分析

3.1混凝土试块多次爆破试验结果

混凝土试块共进行9次爆破试验，第9次爆破后试块破坏，记录试块表面各测点垂向爆破振动波形及速度，振动波形见图2。据测试所得测点爆破振动波速值，利用萨道夫斯基公式对每次爆破后各测点振动速度值回归获得试块表面爆破振动衰减系数α及K值，测试结果见表1。

据超声波检测仪对试块爆破前后波速测试结果，计算损伤值见表2。

3.2混凝土试块多次爆破测试结果分析

为分析混凝土试块表面爆破振动速度传播规律，据表1数据绘制各次爆破后试块测点振动速度随距离增大的变化曲线见图3，据表2数据绘制各测点损伤值随爆破作用次数增加变化曲线见图4。

为进一步分析爆破振动随爆破作用次数增加的变化规律，据表1数据绘制每次爆破后测点振速随爆破次数增加的变化曲线见图5，每次爆破后振动衰减系数α，K值随爆破作用次数增加变化曲线见图6。

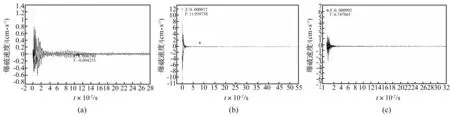
图2　实测爆破振动波形Fig.2 Measured blasting vibration waveform

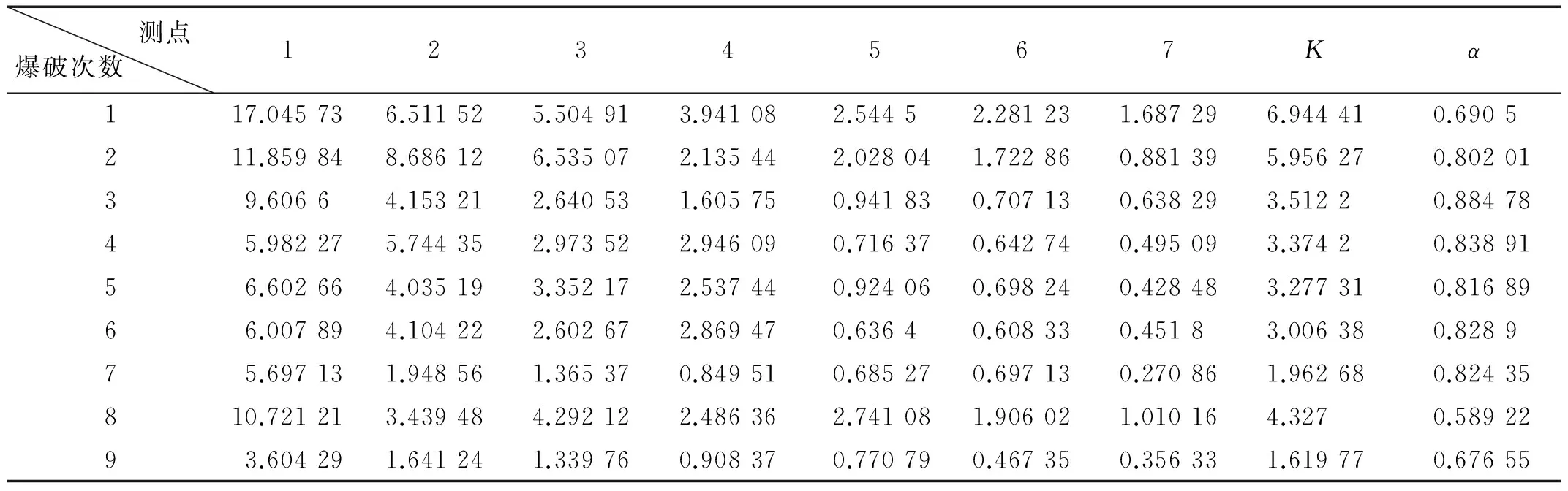
测点爆破次数 1234567Kα117.045736.511525.504913.941082.54452.281231.687296.944410.6905211.859848.686126.535072.135442.028041.722860.881395.956270.8020139.60664.153212.640531.605750.941830.707130.638293.51220.8847845.982275.744352.973522.946090.716370.642740.495093.37420.8389156.602664.035193.352172.537440.924060.698240.428483.277310.8168966.007894.104222.602672.869470.63640.608330.45183.006380.828975.697131.948561.365370.849510.685270.697130.270861.962680.82435810.721213.439484.292122.486362.741081.906021.010164.3270.5892293.604291.641241.339760.908370.770790.467350.356331.619770.67655

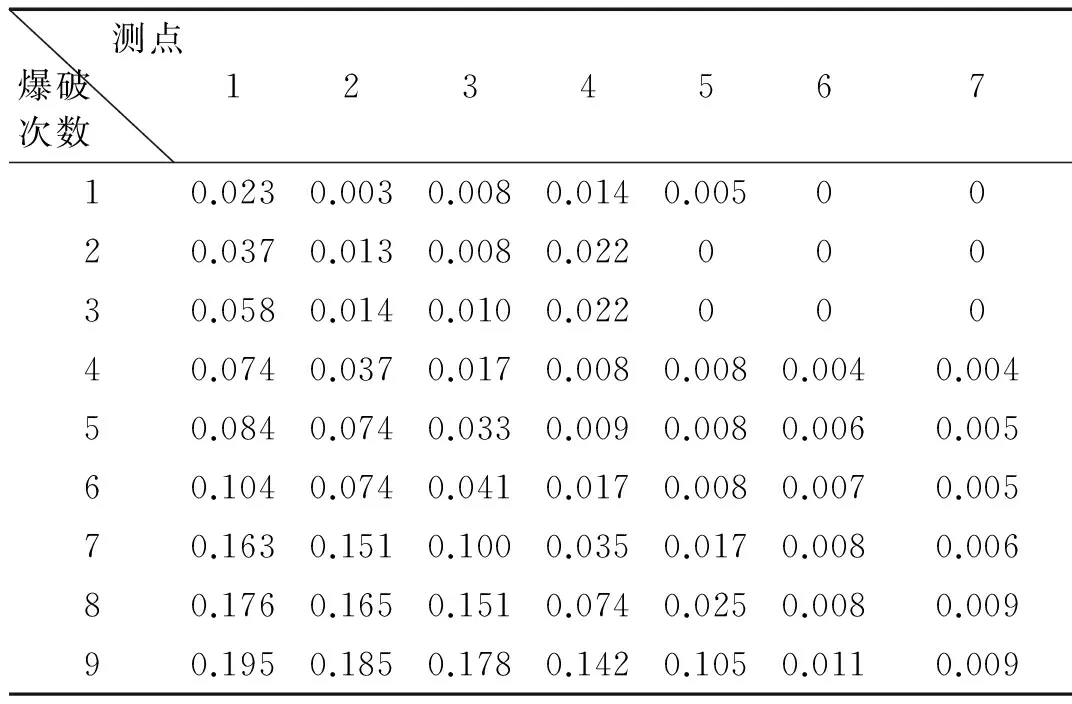
表2　爆破损伤测试结果

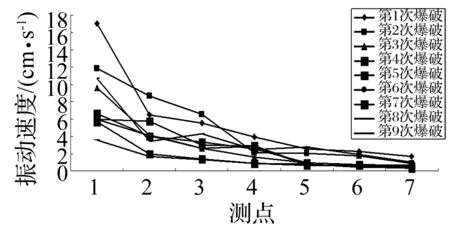
图3　爆破振动速度与测点距离关系Fig.3 Relationships between vibration velocity and distance

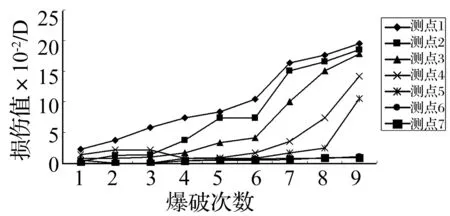
图4　测点损伤值与爆破作用次数关系Fig.4 Relationships between damage value and blasting times

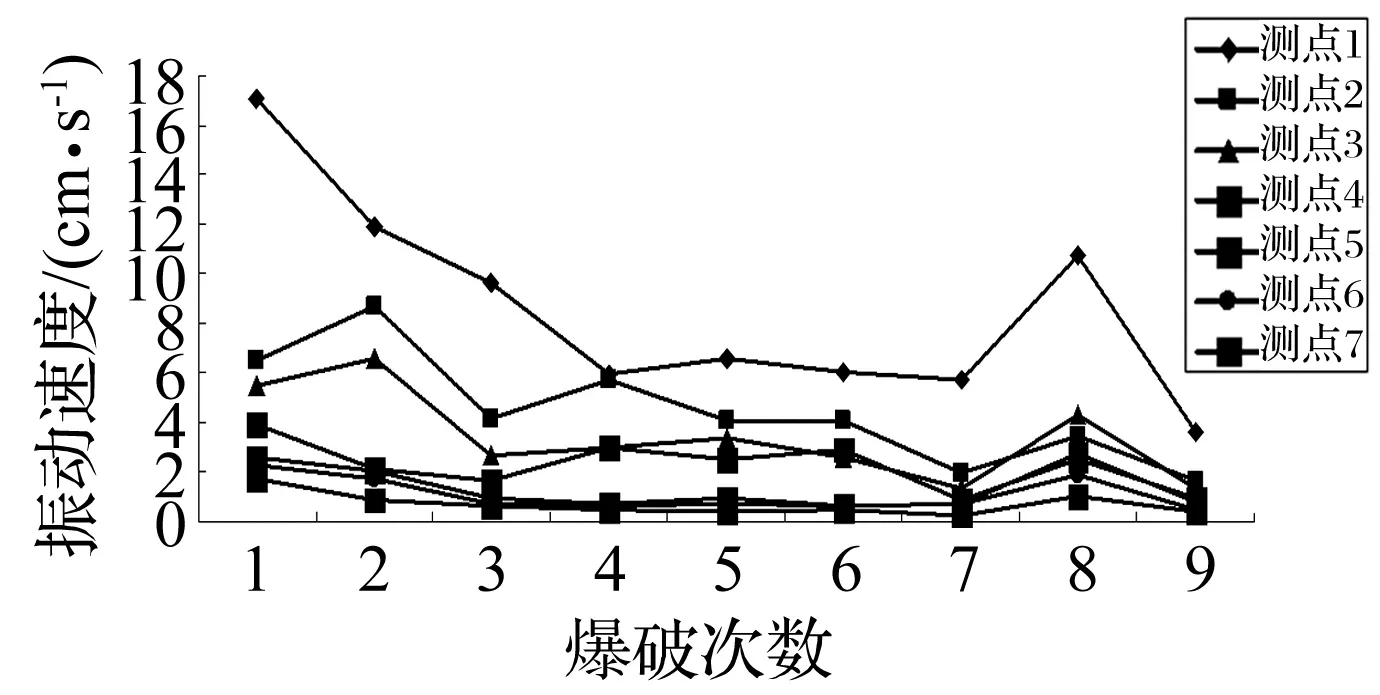
图5　测点振速与爆破作用次数关系Fig.5 Relationships between vibration velocity and blasting times

图6　衰减系数α，K值与爆破作用次数关系Fig.6 Relationships between α，K and blasting times

(1) 由图3看出，每次爆破测点振速沿炮孔中心纵向随距离增大而减小，且爆源近区1、2测点振速快速衰减，中远区、远区3～7测点缓慢衰减。

介质点振动由爆破地震波传播过程对其扰动作用产生，地震波传播为能量通过介质点扰动向爆源四周扩散传递过程，由于转换为爆破地震波的能量只占炸药爆炸释放能量的小部分，且在爆破地震波从爆源向地面传播过程中随传播距离增大，一方面波阵面不断扩大，另方面则因介质内阻尼吸收作用，使爆破地震波能量及振幅不断衰减。式(1)表明条件一定时质点振速随距离增大呈指数衰减。介质衰减作用大小与地震波振动频率有关，对高频振动，介质阻尼作用较大，即高频振动含量更易被吸收，且爆源近区形成粉碎区，炸药爆炸能量损耗严重，导致离爆源较远处高频振动分量被显著衰减，低频成分相对较大，故爆源近区质点振速衰减较快，中远区、远区衰减较慢。

(2) 由图4看出，各测点爆破损伤值随爆破次数增加持续增大，但近区测点损伤值较中远区大，且近区测点损伤值处在较高值阈内缓慢增长；中远区测点损伤值则随爆破次数增加分为初期缓慢增加与后期突然增大两阶段。

混凝土试块近区爆破损伤主要由爆炸应力波作用及爆生气体驱动作用产生的宏观断裂损伤，爆炸应力波随距离增加迅速衰减，故爆破近区损伤快速降低。中区、远区爆破损伤主要由爆炸应力波与爆生气体潜在及间接扰动作用引起，累积损伤断裂演化经历物理力学性能逐渐劣化，宏观及整体力学性能损伤劣化程度增加、混凝土试块整体性与承载力急剧降低突然失稳破坏3个阶段[9-11]。

爆破作用次数较少时由应力集中作用仅能引起初始裂纹尖端处介质晶粒的错动、滑移，该局部影响幅度、范围较小，故初期损伤值累积增长速度缓慢，处于损伤累积演化的初始损伤阶段及细观裂纹形成、扩展阶段，但此不可逆的错动、滑动不断累积叠加，随爆破作用次数继续增加损伤累积效应愈明显，动态应力强度因子增大至混凝土动态断裂韧度，细观裂纹转化为宏观主裂缝，混凝土试块的完整性及力学性能大幅下降，宏观主裂缝加速扩展直至混凝土试块破坏，致中远区测点损伤值在爆破作用次数达到一定值后呈突变过程。

(3) 由图5看出，各测点爆破振速随爆破作用次数增加总体减小，且爆源近区质点振速减小幅度较中远区测点明显，中远区测点振速仅有小幅降低，但随爆破作用次数继续增大各测点振速存在突增过程。随爆破作用次数增加混凝土试块内部损伤不断发展(图4)，应力波携带能量更多的被介质吸收，衰减系数不断增大，导致测点振速随爆破作用次数增加而降低。

爆破近区损伤主要为爆炸应力波作用及爆生气体驱动作用产生的宏观断裂损伤，且爆炸应力波随距离增加迅速衰减，故爆破近区损伤快速降低。中区爆破损伤则主要由爆生气体准静态应力场作用引起，损伤衰减缓慢；远区爆破损伤主要由爆炸应力波与爆生气体潜在与间接扰动作用及边界反射波作用引起，且试验药量较小，故远区爆破损伤值及变化幅度较小，呈近似平稳状态。

混凝土试块承受爆破作用次数较少时，其内部初始裂纹基本不扩展，但由于应力集中作用，裂纹尖端处介质晶粒结构在爆破作用后均发生错动、滑移，该错动、滑移不可逆，且随爆破作用次数增加累积叠加，致裂纹尖端发生局部损伤及变形引起混凝土试块的物理力学性能逐渐劣化，但试块宏观与整体力学性能不会发生明显劣化。爆破作用次数增加裂纹尖端局部损伤变形累积引起初始裂纹起裂扩展逐渐形成细观裂纹，次数继续增加则细观裂纹逐渐贯通使混凝土力学参数劣化加剧形成宏观裂缝，致试块内部损伤逐渐增大，表面质点振速缓慢降低。宏观裂缝形成时混凝土内部的细观裂纹数量减少，仅需较少能量即致主裂缝宽、长度增大，此时应力波携带的能量转化为地面质点振动能量增大，测点振速存在突增过程，爆破时爆炸能量沿宏观裂缝泄露，质点振速又会降低。

(4) 由图6看出，振动衰减系数α随爆破作用次数增加总体上缓慢增加，但次数继续增加时则存在小幅度减小过程；K值随爆破作用次数增加总体呈降低趋势，且降低幅度减小。

α与K反映爆破场地条件及振动波传播介质的地质条件,可通过爆破试验所得介质质点振速及药量、距离实测数据，利用最小二乘法求得。爆破作用次数增加爆破损伤持续缓慢增大(图4)，必会增大爆破振动传播过程的衰减速度。本试验过程中爆破振动测点有5个在中、远区，仅2个在近区，因此α值及变化规律主要受中、远区爆破振速传播与衰减过程决定，α随爆破作用次数增加缓慢增大。K值随试块质量损伤劣化呈降低趋势。随爆破作用次数继续增加各测点振速存有突增过程，该过程由质点振速计算式(1)可直接反映介质完整性增强，故α值减小，K值增大。

4结论

(1) 单次爆破测点振动速度沿炮孔中心纵向随距离增大而减小，且爆源近区测点振动速度快速衰减，中、远区缓慢衰减。

(2) 测点爆破损伤值随爆破作用次数增加持续增大，但近区测点损伤值较中远区大，且近区测点损伤值处在较高值阈内缓慢增长；中远区测点损伤值随爆破次数增加分初期缓慢增加、后期突增两阶段。

(3) 各测点爆破振动速度随爆破作用次数增加总体减小，且爆源近区测点振速减小幅度较中远区明显，中远区测点振速仅小幅度减小；爆破作用次数继续增大时，各测点振速存有突增过程。

(4) 爆破振动衰减系数α随爆破作用次数增加总体缓慢增加，但爆破作用次数继续增加时存在小幅度减小过程；K值随爆破作用次数增加总体呈小幅度减小趋势。

(5) 多次爆破作用下确定振动安全阈值及振动波传播衰减规律需充分考虑爆破振动损伤累积效应，仅以单次爆破振动测试结果分析振动传播及衰减规律进行安全评价不科学。

参 考 文 献

[1] 熊代余,顾毅成. 岩石爆破理论与技术新进展[M]. 北京：冶金工业出版社,2002.

[2] 姚强，杨兴国,陈兴泽,等.大型地下厂房开挖爆破振动动力响应数值模拟[J]. 振动与冲击, 2014, 33(6):66-70.

YAO Qiang, YANG Xing-guo, CHEN Xing-ze, et al. Numerical simulation of dynamic response of large underground powerhouse subjected to blasting vibration[J]. Journal of Vibration and Shock, 2014, 33(6):66-70.

[3] 朱传统,张正宇,佟锦岳,等. 爆破对新浇筑混凝土的影响和控制标准的研究[J]. 爆破,1990,7(3):28-32.

ZHU Chuan-tong, ZHANG Zheng-yu, TONG Jin-yue,et al. Study on the influence of blasting on the new concrete and its control standards [J]. Blasting,1990,7(3):28-32.

[4] 高鸣安,吴新霞. 新浇大体积混凝土安全爆破振动控制标准[J]. 人民长江,1998,29(4):11-13.

GAO Ming-an, WU Xin-xia. Analysis on control standard of blasting security for fresh mass concrete[J]. Yangtze River,1998,29(4):11-13.

[5] 陈明,卢文波. 超早期混凝土爆破安全振动速度的讨论[J]. 工程爆破,2006,12(2):79-81.

CHEN Ming, LU Wen-bo. Safety vibration velocity of fresh concrete under blastingvibration[J]. Engineering Blasting,2006,12(2):79-81.

[6] 宋光明. 爆破振动小波包分析理论与应用研究[D]. 湖南：中南大学,2001.

[7] 吕涛,李海波,周青春,等. 传播介质特性对爆破振动衰减规律的影响[J]. 防灾减灾工程学报,2008,28(3):335-341.

LÜ Tao, LI Hai-bo, ZHOU Qing-chun,et al. The influence of the characteristic of medium on the attenuation law of propagation of vibration due to blasting[J]. Journal of Disaster Prevention and Mitigation,2008,28(3):335-341.

[8] 褚怀保,杨小林,梁为民,等. 煤体爆破损伤规律模拟试验研究[J]. 采矿与安全工程学报, 2011, 28(3):488-492.

CHU Huai-bao,YANG Xiao-lin, LIANG Wei-min,et al. Experimental study on the blast damage law in simulation coal[J]. Journal of Mining & Safety Engineering, 2011, 28(3):488-492.

[9] 李朝阳,宋玉普,车轶. 混凝土的单轴抗压疲劳损伤累积性能研究[J]. 土木工程学报,2002, 35(2):38-40.

LI Chao-yang,SONG Yu-pu,CHE Yi. Study on cumulative damage behavior of concrete under uniaxial cyclic load[J]. China Civil Engineering Journal, 2002, 35(2):38-40.

[10] Li X B, Lok T S, Zhao J. Dynamic characteristics of granite subjected to intermediate loading rate[J]. Rock Mechanics and Rock Engineering, 2005, 38(1):21-39.

[11] 闫长斌,王贵军,王泉伟,等. 岩体爆破累积损伤效应与动力失稳机制研究[M]. 郑州：黄河水利出版社,2011: 82- 90.

基金项目：国家自然科学基金项目(11542019,50874039)；河南省骨干教师资助项目；河南理工大学骨干教师资助项目；河南理工大学博士基金

收稿日期：2014-11-25修改稿收到日期：2015-01-13

中图分类号:TD235.1+1

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.02.029

Experiments on propagation of blasting vibration based on damage accumulation

CHU Huai-bao, YE Hong-yu, YANG Xiao-lin, LIANG Wei-min, YU Yong-qiang

(College of Civil Engineering, Henan Polytechnic University, Jiaozuo 454000, China)

Abstract:In order to further reveal the propagation attenuation of blasting vibration based on damage accumulation, damage accumulation and blasting vibration experiments on a concrete block were designed. The results show that the damage values at measured points increase successively with the increase of the number of blasting times. The variation of damage value can be divided into two stages in middle and far areas: a slow increase at early stage and a quick increase at later stage. The vibration velocities of single blasting at measured points decrease with the distance increasing, and the vibration velocities at measured points in the near area decrease faster than in the middle and far areas. The blasting vibration velocities at measured points decrease generally with the increase of the number of blasting times, near the explosion source it decreases more rapidly, but in middle and far areas, it decreases in small amplitude and slowly. And with the increase of the number of blasting times, the vibration velocity experiences a process of sudden increase. The vibration attenuation coefficient α increases slowly with the increase of the number of blasting times, however, the value of K reduces, and both of them undergo a process of small amplitude distortion. Under the condition of repeated blasting, in the determination of the safety threshold and propagation attenuation (the value of K and α) of the blasting vibration, the blasting vibration damage accumulation effect should be taken into account.

Key words:damage accumulation; blasting vibration; propagation attenuation laws; experimental study

第一作者 楮怀保 男，博士，副教授，1978年12月生