多共振消声器串联系统声学特性分析及应用

高书娜， 赵金斗

(西南大学 工程技术学院, 重庆　400716)



多共振消声器串联系统声学特性分析及应用

高书娜， 赵金斗

(西南大学 工程技术学院, 重庆400716)

摘要：针对内燃机进气系统需良好的低频消声效果而可用空间有限的问题，研究多个消声器串联后的声学特性。基于共振消声器集中参数模型，推导消声器串联后系统主消声频率公式并验证。结果表明，双共振消声器串联系统有两主消声频率，即小于、大于下端消声器的偏频；增加体积比时较小的接近偏频，较大的远离偏频；长度比等于1、面积比小于等于1时串联系统所需体积小。串联系统消声器结构参数均相同时主消声频率个数与消声器个数相同。基于此，对某商用车进气系统进行降噪设计，使200 Hz以内的传声损失整体提高约5 dB。

关键词：串联；共振消声器；集中参数模型；主消声频率；总体积

汽车进气噪声主要集中在50～400 Hz的中低频范围内，常并联多个不同体积的共振消声器实现降噪[1-2]。而多个共振消声器并联只能实现传声损失的线性叠加，且为实现良好的低频消声效果，需将共振腔体积设计的较大[3-4]。实际上，因车辆可利用空间有限，难以布置目标体积的共振消声器。为此，已有对共振消声器串联的消声特性进行研究[5]，但只针对几个不同形式的串联结构，未给出支持理论、对串联结构展开深入细致分析及揭示一般性规律。

本文通过推导共振消声器串联系统基础理论，深入分析串联系统声学特性及一般性规律，为工程串联式消声器设计提供理论依据；并将设计的消声器用于某车进气系统评价消声效果，验证理论设计的可行性。

1双共振消声器串联系统基础理论

共振消声器传声损失公式计算精度不足，本文针对主消声频率进行讨论。

1.1主消声频率公式

图1　双共振消声器串联系统类比示意图Fig.1 Sketch map of analogy of the series-wound system of double-resonant silencer

设系统阻尼系数为c，基于类比系统无阻尼自由振动方程推导串联系统主消声频率公式。类比系统无阻尼自由振动方程为

(1)

式中：

设z2=0，相当于仅下端消声器工作，则系统的圆频率为

(2)

设z1=0，相当于仅上端消声器工作，则系统的圆频率为

(3)

式中：ω01及f01，ω02及f02为系统偏频。

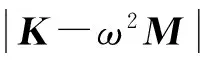
(4)

得

(5)

设m2=am1，k2=bk1，将式(2)代入，式(5)可写为

(6)

串联系统主消声频率为

频率比为

(8)

设体积比RV=V1/V2，面积比RS=S1/S2，长度比Rl=l1/l2，则有

(9)

(10)

为提高计算精度，常用短管声学长度l1a=l1+δ1代替实际长度l1，δ1为修正值。经大量计算分析知，采用声学长度虽研究结论基本无变化，却增加串联消声器系统设计的复杂程度，故仍用实际长度。

1.2主消声频率公式验证

消声器实物试制及实验周期较长，故采用虚拟试验法先期验证。利用有限元法计算传声损失，统计主消声频率，验证理论推导结果。研究知，显著影响消声器传声损失的有共振腔体积、短管截面积及长度、主管截面积，而消声器具体形状(矩形或圆形等)对传声损失影响较小[8-9]。为便于建模均用矩形。

所建单共振消声器有限元模型见图2(a)。模型参数为共振腔体积V1=200×200×100(mm3)，短管截面积S1=30×30(mm2)，短管长度l1=9 mm，主管截面积=50× 50 (mm2)。传声损失见图2(b)，可见在500 Hz内只有一个主消声频率，大小为100 Hz。在消声器模型上方串联一共振消声器，模型参数为l2=l1，S2=S1，V2=V1/(0.1～10)，得Rl=1，RS=1，RV= 0.1～10。

图2　单共振消声器有限元模型及传声损失Fig.2 The finite element model and transmission loss ofa single-resonant silencer

用有限元法计算系统主消声频率，用式(7)求得f01= 100 Hz，Rl= 1，RS= 1，RV= 0.1～10时双共振消声器串联系统主消声频率，结果见图3。由图3看出，公式与有限元法计算结果非常接近，误差在4%以内，两者吻合较好。表明推导的双共振消声器串联系统主消声频率公式计算精度较高。

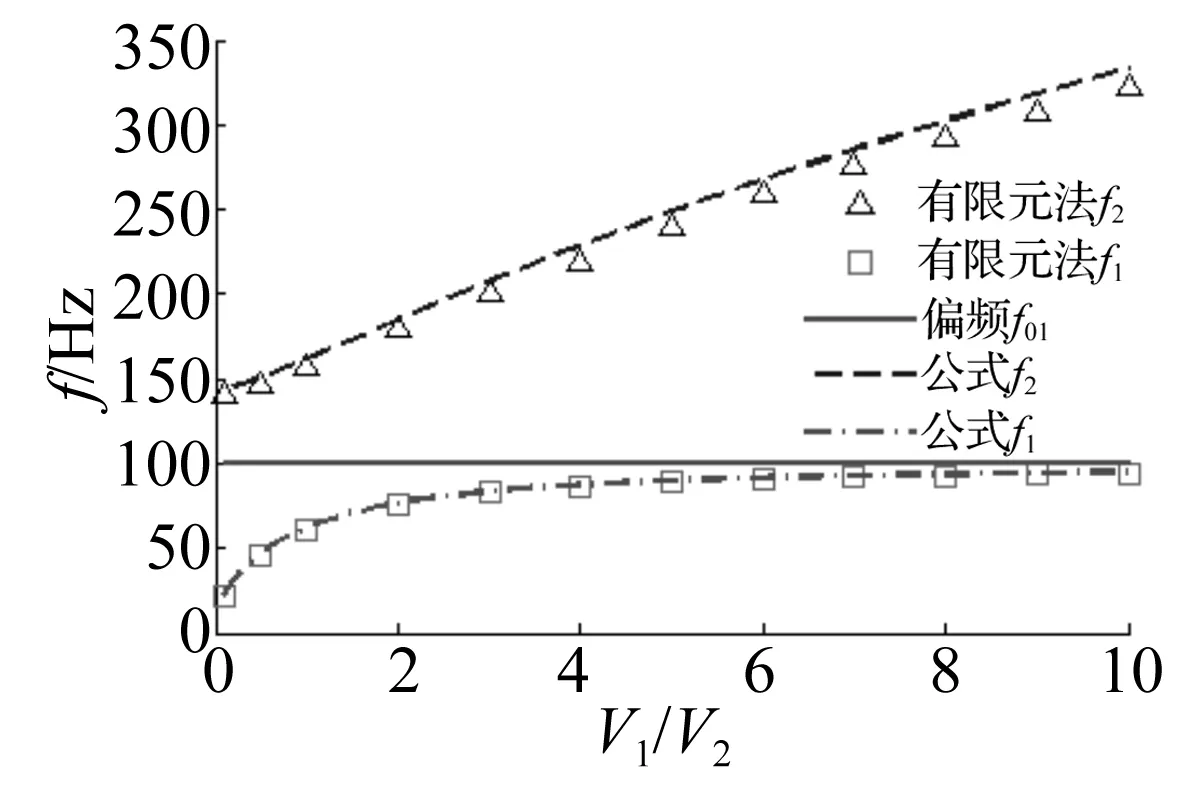
图3　主消声频率与体积比关系曲线Fig.3 Relationship between the main resonant frequencies and the volume ratio

1.3声学特性分析

1.3.1主消声频率分布

据式(8)分析频率比Rf的取值范围，找出主消声频率分布特点。由于Rl、RS、RV均大于零，则a、b也大于零，故频率比Rf有两个正值。式(8)等号两边取平方

(11)

因

(12)

且

(13)

式(12)减去式(13)，有

式(12)加上式(13)，有

因(b-a)<(b+a)，故不等式成立，即

在不等式两边分别加2a，不等号方向不变，即

不等式两边分别除以2a，有

(14)

(15)

因此，频率比Rf分别有个小于1、大于零及大于1的值，即双共振消声器串联系统主消声频率有小于、大于下端单共振消声器主消声频率f01各1个。由此得主消声频率分布为：在单共振消声器上方串联一共振消声器后系统产生两个主消声频率，大小由式(7)计算，分布于单共振消声器主消声频率两边。

1.3.2主消声频率特点

基于式(8)～式(10)，给定Rl、RS的值，求出频率比Rf随体积比RV变化规律，讨论主消声频率特点。并求出分别用串、并联系统取相同Rl、RS值时所得相同主消声频率所需总体积Vall。典型计算结果见图4。由图4看出，①Rl= 1，RS= 2时，随体积比增加两频率比均逐渐升高。较高的基本呈线性升高，远离1；较低的基本呈对数升高，无限接近1。在RV= 4时串、并联系统体积相同，RV< 4时串联系统所需体积小，而RV> 4时并联系统所需体积小。②Rl= 1，RS= 1时，随体积比增加两频率比值均逐渐升高。较高的基本呈线性升高，远离1；较低的基本呈对数升高，无限接近1。所需串联系统体积始终小于并联系统。③Rl= 1，RS= 0.5时，随体积比增加两频率比值均逐渐升高。较高的不再呈线性升高，仍远离1；较低的仍基本呈对数升高，无限接近1。所需串联系统体积始终小于并联系统。

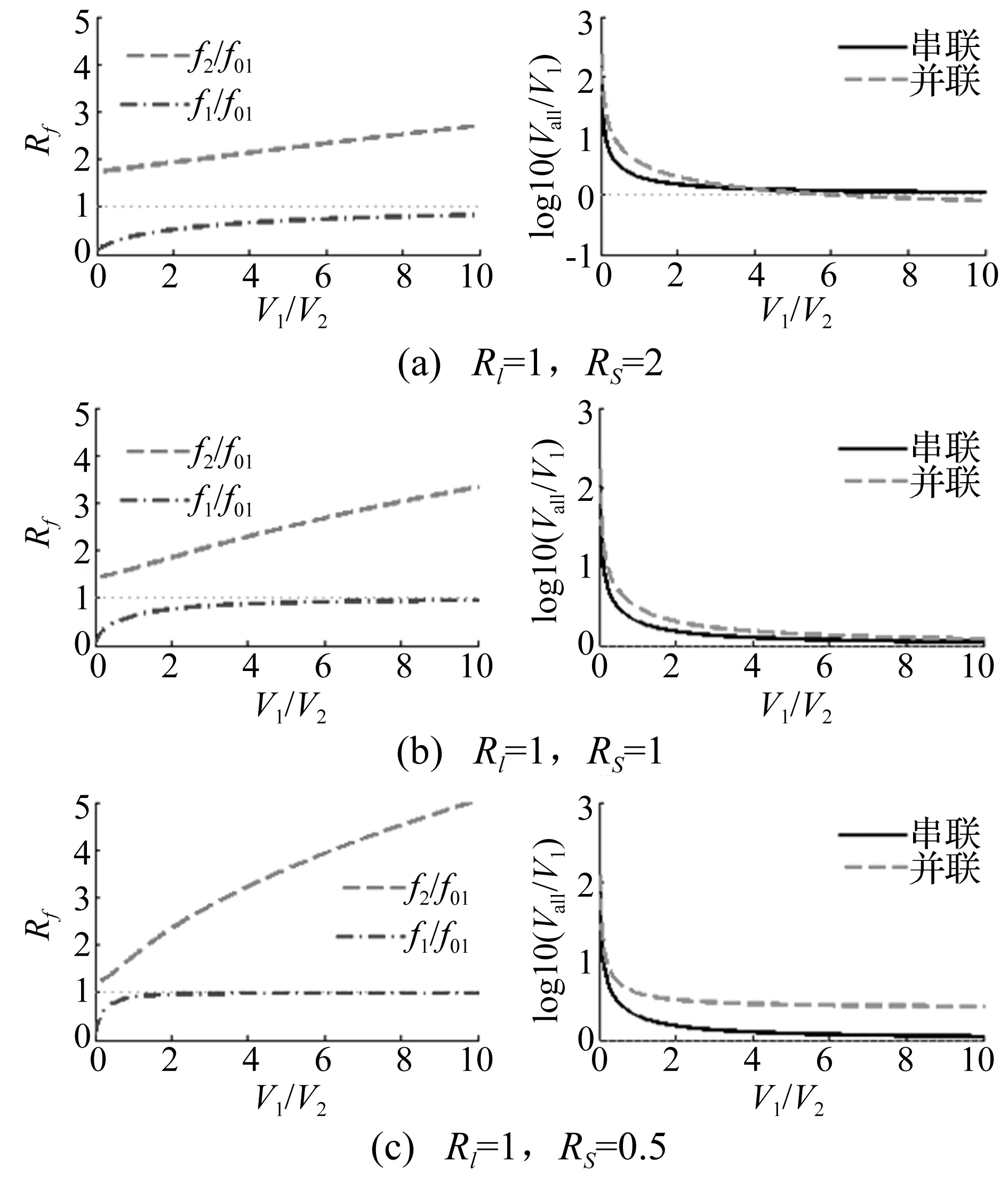
图4　频率比、总体积与体积比关系Fig.4 Relationship amongfrequency ratioandvolume to the volume ratio

因此，串联系统两主消声频率特点为：体积比增加，较高的远离偏频f01，较低的无限接近偏频f01；取Rl= 1，RS≤1时，串联系统所需体积小(该结论已获得验证，篇幅所限未列出)。当两目标消声频率确定后建议取Rl=1，RS≤1，既能实现目标，又能减小所需空间。

2多共振消声器串联系统基础理论

为全面掌握串联式共振消声器主消声频率基础理论，讨论3个或以上共振消声器串联。

2.1主消声频率计算

3个或以上共振消声器串联系统，类比为多个质量-阻尼-弹簧系统串联，求解主消声频率特征方程为

(16)

式中：

(17)

(18)

式(17)、(18)均较复杂。虽已有一元三次、四次方程解的一般形式，但因解的判定方法及一般公式较复杂，实际工程直接应用较少，且据Galois理论，五次及以上线性方程无一般解的公式，需借助数值分析方法求近似解。若实际需多个共振消声器串联系统时，可据具体情况给定结构基本参数再计算。此处仅对串联的几个消声器结构参数相同情况进行讨论，集中质量、刚度系数均相同，则式(17)可写为

(19)

式(18)可写为

(20)

消声器结构参数l1、S1、V1值给定后，可据以上解求出3个或4个共振消声器串联系统的主消声频率。

由以上分析知，结构参数相同的有几个消声器串联，系统则产生几个主消声频率，可以此类推。该结论可为工程用多个共振消声器串联时，系统主消声频率预估提供重要依据。

2.2结论验证

在1.2节单共振消声器上方分别串联2、3个结构参数相同消声器，利用有限元法计算系统传声损失，结果见图5，主消声频率统计及利用公式所得见表1。由图5、表1可知，系统主消声频率个数与串联共振消声器个数相同；且主消声频率公式计算结果与有限元结果非常接近，误差在5%以内，两者吻合较好。从而验证理论推导结果的正确性。

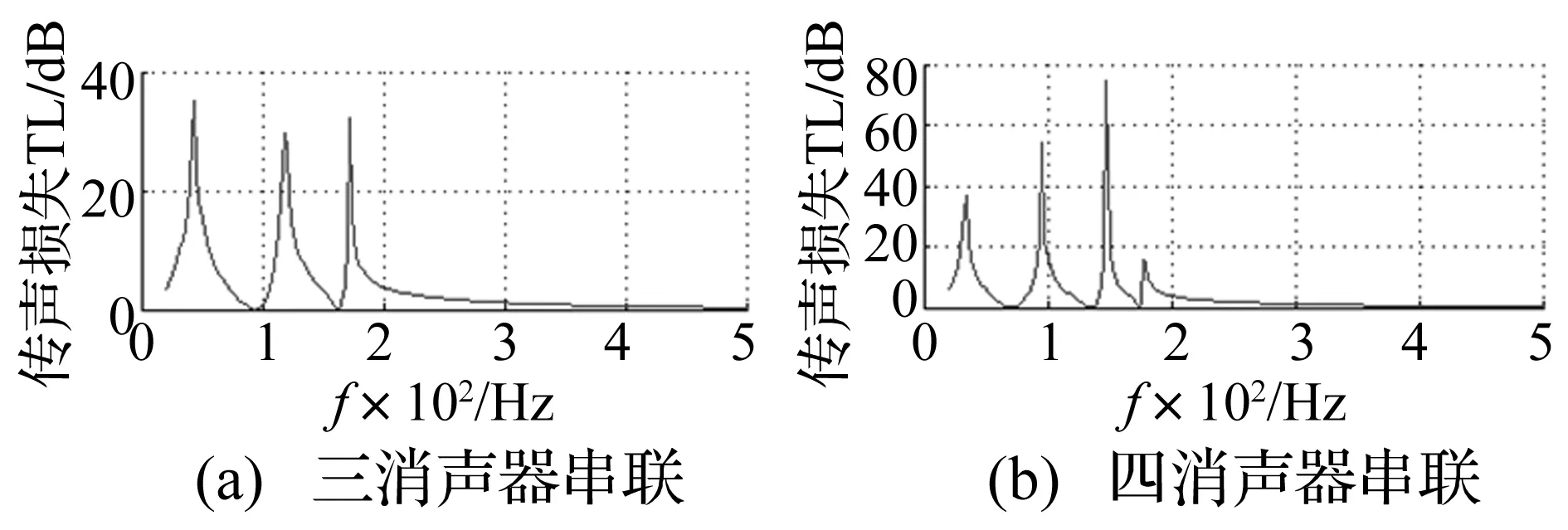
图5　多消声器串联系统传声损失Fig.5 The transmission loss of the series-wound system of multi-resonant silencer

3某商用车进气系统应用

3.1原车进气噪声分析

某商用车全负荷加速时发动机进气歧管处噪声频谱特性见图6(a)。由图6(a)看出，进气系统噪声主要集中在100～600 Hz范围内，且具有明显的阶次特性。

表1　多共振消声器串联系统的主消声频率

随发动机转速变化噪声峰值频率亦变化。高位进气管口处噪声见图6(b)。由图6(b)看出，经空滤器、高位进气管消声，200～2 000 Hz频带下噪声明显降低，尤其250～600 Hz处噪声峰值降低明显；但2阶(50～100 Hz)、4阶噪声(100～200 Hz)几乎未降低，实车试验时能清晰听到该阶次噪声。

图6　某商用车进气噪声Fig.6 The intake noise of a commercial vehicle

因此，该车型进气系统需重点提高50～200 Hz低频处消声量。该频带频率较低，若采用扩张腔消声器，进气系统尺寸须设计的大并不现实。故常用共振式消声器，效果较好；但进气噪声峰值频率随发动机转速变化而变化，共振消声器消声频带较窄且具有较强的频率选择性。若在50～200 Hz整个频带均有较好消声效果，则需并联多个共振消声器，会增加进气消声器系统结构的复杂程度及成本，故宜用串联式共振消声器。因该系统会产生明显的通过频率(图5)，需再并联共振消声器以提高消声低谷。为使结构尽量简单，拟设计双共振消声器串联，再并联一个用于提高低谷消声量，将产生3个消声频率。

3.2进气消声器设计与效果评价

原车进气系统传声损失见图7。由图7看出，在低频50～200 Hz处消声量较小，低于20 dB。整体提高此处消声量，可均布3个目标消声频率67 Hz、134 Hz及200 Hz。考虑消声器设计中结构参数取整，将双共振消声器串联系统目标主消声频率定为70 Hz及200 Hz。

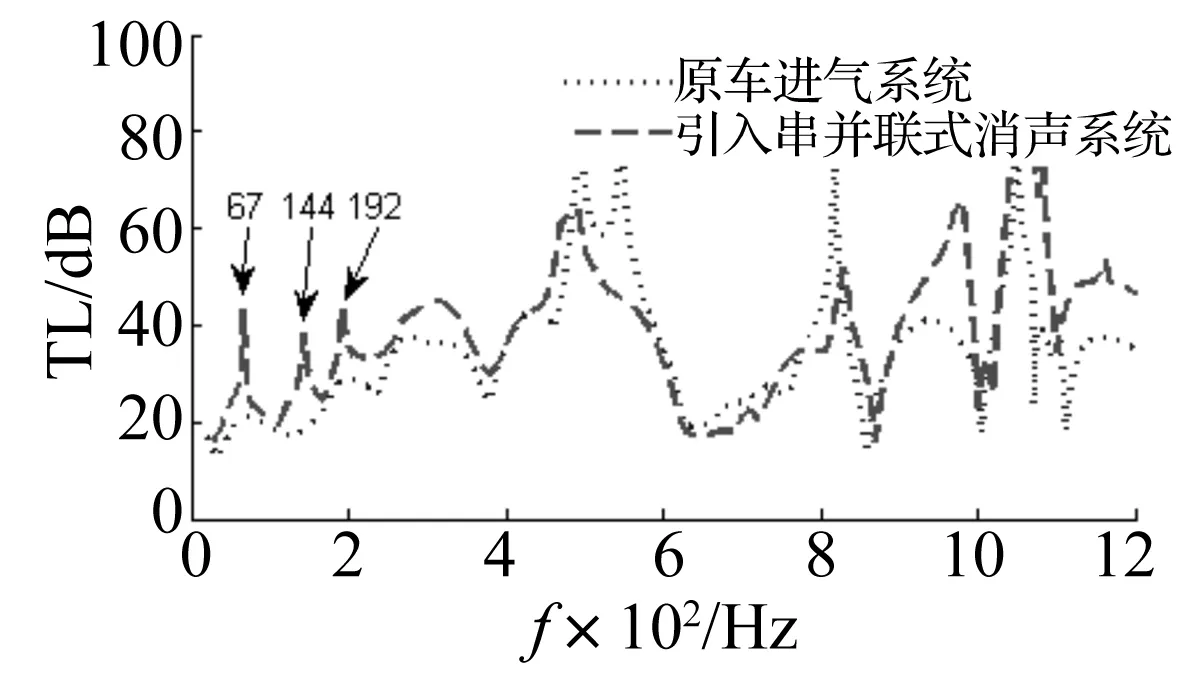
图7　某商用车进气系统传声损失Fig.7 The transmission loss of the intake system of a commercial vehicle

由Rl、RS的取值范围，选Rl= 1、RS= 1及0.5。据式(7)及两个目标主消声频率推导f01关于RV的公式，绘制曲线，两条曲线交点即为f01、RV的解，见图8。由图8看出，RS=1、0.5时均分别有两个解(因f01为关于RV的二次函数)，提取结果见表2。

图8　f01关于RV的关系曲线Fig.8 Relationship between f01 and RV

据实车空间设计下端消声器结构参数为：l1= 50 mm，S1= 40 mm×40 mm；V1据表2偏频f01获得。上端串联消声器结构参数据表2中Rl、RS、RV获得。可见，当Rl=1、RS=1、RV=0.72时所需总体积最小，因此确定用该组参数。计算设计的双共振消声器串联系统传声损失，据两消声峰值间低谷设计并联共振消声器结构参数，并将设计的消声器用于研究车型进气系统(传声损失见图7)。可见，引入串并联式消声器后在67 Hz、144 Hz、192 Hz处产生3个消声峰值，且200 Hz以内传声损失整体提高约5 dB，低频内消声效果明显提高。由此证明串联式消声器理论设计的可行性。

4结论

基于共振消声器的集中参数模型，推导、验证两个及以上共振消声器串联系统主消声频率计算公式，讨论主消声频率特点，并对某商用车进气系统进行降噪设计，结论如下：

(1) 双共振消声器串联系统有两个主消声频率，即小于、大于偏频f01。该两主消声频率随体积比增加，较高的远离偏频f01，较低的无限接近于偏频f01；长度比等于1、面积比小于等于1时串联系统所需体积小。

(2) 串联系统各消声器结构参数相同时，系统主消声频率个数与消声器个数相同。本文设计的串并联式消声器用于某商用车进气系统后，200 Hz以内传声损失明显提高。

参 考 文 献

[1] 庞剑,谌刚,何华. 汽车噪声与振动[M]. 北京:北京理工大学出版社, 2006.

[2] 刘丽媛,季振林. 涡轮增压发动机进气消声器设计与声学性能数值分析[J]. 振动与冲击,2011, 30(10): 193-196.

LIU Li-yuan, JI Zhen-lin.Design ofturbochargedengineintake silencersand numerical analysis for their acoustic performance [J]. Journal of Vibration and Shock, 2011, 30(10): 193-196.

[3] Montenegro G, OnoratiA. Modeling of silencers for i.c. engine intake and exhaust systems by means of an integrated 1D-multid approach[J]. SAE International Journal of Engines, 2008,1(1): 466-479.

[4] Lee I J, Selamet A, Kim H, et al.Design of a multi-chamber silencer for turbocharger noise[J]. SAE International Journal of Passenger Cars-Mechanical Systems, 2009,2(1):1339-1344.

[5] 毕嵘,刘正士,王慧,等. 多腔共振式消声器的声学特性分析[J]. 农业机械学报, 2008, 39(10): 48-51.

BI Rong, LIU Zheng-shi, WANG Hui, et al. Analysis ofacoustical performance of multi-chamber helmholtz resonators[J]. Transactions of the Chinese Society for Agricultural Machinery, 2008, 39(10): 48-51.

[6] 马大酞. 声学手册[M]. 北京: 科学出版社, 1983.

[7] 何渝生. 汽车噪声控制[M]. 北京: 机械工业出版社, 1995.

[8] 阮登芳. 共振式进气消声器设计理论及其应用研究[D]. 重庆: 重庆大学, 2005.

[9] 阮登芳,邓兆祥,杨诚.共振式消声器声学性能分析[J]. 内燃机工程, 2006,27(1): 66-70.

RUAN Deng-fang, DENG Zhao-xiang, YANG Cheng.Analysis of acoustic performance of the resonant silencer[J]. Chinese Internal Combustion Engine Engineering, 2006,27(1): 66-70.

[10] E·阿廷,著.李同孚,译. Galois理论[M]. 黑龙江: 哈尔滨工业大学出版社, 2011.

基金项目：中央高校基本科研业务费专项资金资助(XDJK2014C133; XDJK2013C066)

收稿日期：2014-10-22修改稿收到日期：2015-01-07

中图分类号:TB535 +.2

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.02.032

Acoustic performance analysis of the series-wound system of multi-resonant silencer and its application

GAO Shu-na, ZHAO Jin-dou

(College of Engineering and Technology, Southwest University, Chongqing 400716, China)

Abstract:The good performance of low frequency noise reduction is usually in contradiction with the limited space of intake system of internal combustion engine. Aiming at this problem, the acoustic performance of the series-wound system of a multi-resonant silencer was studied. Based on a lumped parameter model of the resonant silencer, the formula for the main resonant frequencies of the series-wound system of multi-resonant silencer were deduced and verified. The study shows that the series-wound system of double-resonant silencer has two main resonant frequencies, where the one is smaller than the bias frequency of the bottom resonant silencer, and the other is bigger. Along with the volume ratio increasing, the smaller resonant frequency gets close to the bias frequency, while the bigger one gets away.The total volume needed in series-wound system is smaller than in parallel system when the length ratio = 1 and the area ratio ≤1. When the structure parameters of the silencers in the series-wound system are the same, the number of the main resonant frequencies equals to the number of the silencers. Based on these conclusions, the intake system of a commercial vehicle was redesigned with the transmission loss below 200Hz increased by about 5dB over all.

Key words:series connection; resonant silencer; lumped parameter model; main resonant frequency; total volume

第一作者 高书娜 女，博士，讲师，1980年12月生