考虑间隙运动副耦合作用的车辆摆振动力学行为分析

姜俊昭， 卢剑伟， 张　辉

(合肥工业大学 机械与汽车工程学院，合肥　230009)



考虑间隙运动副耦合作用的车辆摆振动力学行为分析

姜俊昭， 卢剑伟， 张辉

(合肥工业大学 机械与汽车工程学院，合肥230009)

摘要：车辆转向机构中各间隙运动副之间的动力学耦合会对其动力学响应产生重要影响。以考虑转向机构中间隙运动副耦合作用的非独立悬架车辆为例，基于分析力学建立了六自由度车辆摆振分析模型。应用数值方法分析了车辆摆振系统的动力学响应特性，对其中出现的Naimark-Sacker分岔、混沌等现象做了分析，并从能量传递角度对其摆振机理进行了解释，相关分析结论可为更好地实现车辆摆振控制提供理论支持。

关键词：车辆；摆振；间隙；耦合

过去几十年来，相关学者围绕车辆摆振的动力学机理分析等开展了大量理论与实验研究，为车辆防摆振设计做出了重要贡献。例如，Demic[1]基于转向系统和悬架系统的耦合研究了转向系统参数对重载汽车摆振的影响；Zhuravlev等[2]提出了分段干摩擦理论，考察了转向系统干摩擦对摆振的影响。管迪华等[3]从能量反馈和负阻尼效应等角度研究了轮胎特性及其它结构参数对汽车前轮摆振的影响；郭孔辉[4]基于试验建立了轮胎侧偏特性分析模型，为车辆摆振分析提供了良好的基础。

上述研究分别考察了轮胎、系统结构参数匹配、摩擦等因素对摆振的影响。而对于在役车辆，磨损导致的运动副间隙不断增大，并可能逐步成为影响车辆摆振响应的主导因素[5]。作者所在团队近几年来尝试揭示运动副间隙对摆振系统动力学行为的影响，前期工作中发现间隙运动副之间的动力学耦合对于机构动力学响应的影响不容忽视，因此，有必要对考虑间隙运动副动力学耦合的车辆摆振系统动力学行为进行讨论。

本文以考虑转向传动机构两个间隙运动副之间动力学耦合的车辆为例，建立了考虑间隙运动副之间动力学耦合的车辆摆振系统模型，通过数值算例对其转向轮摆振响应特性进行了探讨，相关分析结论为抑制在役车辆摆振提供了理论支持。

1考虑间隙运动副耦合作用的在役车辆摆振动力学分析模型

以非独立悬架车辆为例，同时考虑转向传动机构中横拉杆和左右梯形臂之间的两个间隙运动副，基于如下假设建立如图1所示的车辆摆振系统动力学分析模型：

(1) 汽车在平直路面上等速直线行驶；

(2) 仅考虑汽车在横向激励下的响应；

(3) 忽略簧载质量对转向系统的影响，计入转向轮与前桥的耦合振动；

(4) 忽略转向操纵机构对摆振的影响，假定方向盘保持前进方向不动，转向直拉杆到转向盘简化为一弹簧阻尼器。

该模型包含六个自由度：左前轮绕主销摆角θ1、右前轮绕主销摆角θ2、前桥绕纵轴线的侧摆角ψ、横拉杆横摆角Φ、横拉杆质心S1沿x和y方向位移Xs、Ys。

1.1间隙运动副描述

图1中O1、O2为右侧间隙副轴销中心与轴套中心，O3、O4为左侧间隙副轴销中心与轴套中心。基于Hertz理论，并计入运动副接触表面的弹性、阻尼及摩擦，间隙运动副接触点的法向力可写为：

P2n=Kδ2n+Cnv2n

(1)

P1n=Kδ1n+Cnv1n

(2)

式中:K为接触刚度；Cn为法向阻尼；δ2n,δ1n分别为左右两侧间隙的法向变形；v2n,v1n分别为左右两侧间隙接触点的法向速度。运动副切向力可以写为：

(3)

(4)

M1=l2(F2ycosΦ2-F2xsinΦ2)+R1(F2ycosβ2-

F2xsinβ2)+F2ye2x-F2xe2y

(5)

M2=l3(F1xsinΦ1-F1ycosΦ1)+R1(F1xsinβ1-

F1ycosβ1)

(6)

式中:β1为O1O2和x轴的夹角；β2为O3O4和x轴的夹角；R1为轴销半径；l2,l3分别为左右梯形臂长度；e2x,e2y分别为左侧间隙副轴套与轴销中心距在x、y方向的投影；Φ2,Φ1分别为转向梯形左右底角；F2x,F2y,F1x,F1y分别为左右侧接触力在x和y向分力。

1.2轮胎模型

本文采用“魔术公式”来描述轮胎的侧偏力，可以写为：

(7)

式中:T1，T2分别为左、右轮胎的动态侧偏力，α1，α2为左、右车轮的侧偏角。Sx,Sy,B,C,D,E为魔术公式参数，一般通过实验测试进行辨识。本文根据厂家提供的规格为215/55R17轮胎的试验数据，通过遗传算法和数值优化算法对公式进行拟合[6]，结果见表1。

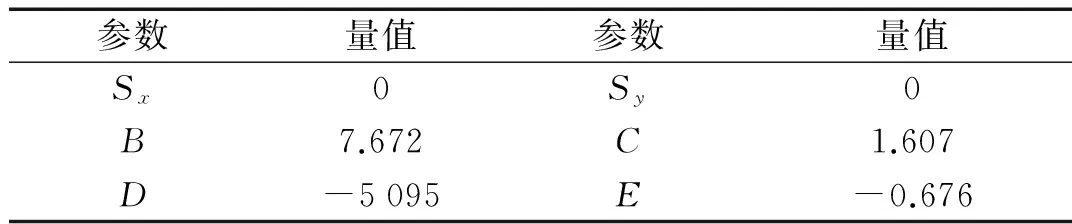
表1　侧向力公式参数辨识结果

1.3摆振模型

运用分析力学的原理，结合以上间隙副模型和轮胎模型，可建立六自由度摆振系统运动方程：

T2(Rγ+ε)-M2=0

(9)

(10)

F1ycosφ-F2ycosφ)-(F1xe1y-F1ye1x)=0

(11)

(12)

(13)

式中:e1x、e1y分别为右侧间隙副轴套与轴销中心距在x、y方向的投影，I1为车轮绕主销的转动惯量；I2为车轮绕其本身旋转轴线的转动惯量；I3为前桥绕其纵轴线的转动惯量；Is为横拉杆绕经过质心垂线的转动惯量；v为车速；R为轮胎滚动半径;c4为车轮绕主销的当量阻尼；k4为轮胎的侧向刚度；k5为轮胎的垂向刚度；γ为主销后倾角；f1为滚动阻力系数；l为主销延长线与地面交点到车轮对称面距离;L为轮距;k2和c2分别为换算到主销的转向机构刚度和阻尼；k3和c3分别为换算到前桥侧摆中心的悬架当量角刚度和角阻尼；σ为轮胎松弛长度；a为轮胎印迹半长度；ε为轮胎拖距。l1为横拉杆长度；m1为横拉杆的质量。

2数值算例及结果讨论

图2为车型参数相同，车速v=55 km/h，间隙均为0.05 mm，考虑左右间隙运动副动力学耦合作用与仅考虑转向机构左梯形臂运动副间隙时的对比分析结果。从中看出，考虑两个运动副间隙时车辆摆振幅值较仅考虑一个运动副间隙时显著增加。图3对两种情况下左轮摆角幅值随间隙的变化做了对比，可见考虑左右间隙运动副耦合作用比仅考虑一个运动副间隙时摆角幅值要大。

图4为车速v=55 km/h，左侧间隙r1=0.05 mm，右侧间隙r2=0.001 mm以及r1=0.001 mm，r2=0.05 mm时的转向轮摆振响应。对比图2，其幅值较仅考虑一个运动副间隙时仍显著增加。当磨损或装配的随机性导致一侧间隙较大时，另一侧间隙即使很小也会与之产生明显的耦合作用。以上分析说明间隙运动副之间的动力学耦合对摆振响应幅值影响较大。

图2 摆振时间历程(r=0.05mm)Fig.2Timehistoryofshimmy(r=0.05mm)图3 摆振幅值变化趋势(v=55km/h)Fig.3Changetrendsofshimmyamplitude(v=55km/h)图4 摆振时间历程(r1≠r2)Fig.4Timehistoryofshimmy(r1≠r2)

图5为车速v=40 km/h，间隙均为0.2 mm，考虑两个间隙运动副动力学耦合及仅考虑一个间隙的摆振响应分析结果。图5(a)所示的系统为拟周期运动，图5(b)所示系统为周期运动。考虑两个间隙时，一侧间隙运动副的接触、碰撞与分离直接影响另一侧间隙的运动，使得摆振形态变复杂。对于本文车型参数，如果间隙继续增大至9 mm时，考虑两个间隙运动副动力学耦合的摆振系统出现混沌现象，如图6(a)所示；而仅考虑一个间隙时系统为3周期运动，如图6(b)所示。尽管这么大的运动副间隙在工程实践中不会出现，但如果车型参数发生变化，有可能在很小的间隙时即出现运动形态方面的显著差异。由此可见，间隙运动副之间的动力学耦合会导致摆振系统稳定性下降，更易引发混沌运动。

图5(a)　考虑两个间隙的左轮摆角响应(r=0.2 mm)Fig.5(a) Dynamic response of left front wheel with consideration of two clearances(r=0.2 mm)

图5(b)　考虑一个间隙的左轮摆角响应(r=0.2 mm)Fig.5(b) Dynamic response of left front wheel with consideration of one clearance(r=0.2 mm)

图6(a)　考虑两个间隙的左轮摆角响应(r=9 mm)Fig.6(a) Dynamic response of left front wheel with consideration of two clearances(r=9 mm)

图6(b)　考虑一个间隙的左轮摆角响应(r=9 mm)Fig.6(b) Dynamic response of left front wheel with consideration of one clearance(r=9 mm)

图7　间隙接触力功率时间历程曲线Fig.7 Time history of power of contact force

考虑间隙耦合作用时，左右两侧间隙接触力做功的功率如图7所示。其正功率均远大于负功率，说明两侧间隙接触力对车轮有能量输入，会加剧摆振。

图8所示为轮胎动能、转向机构势能及横拉杆动能的时间历程对比。其中轮胎动能与横拉杆动能同相，说明轮胎与横拉杆之间有相互激励。由于横拉杆受力为间隙接触力，运动副间隙的动力学耦合作用促使了横拉杆与轮胎的相互激励；轮胎动能与转向机构势能反相，说明摆振过程中轮胎与转向机构之间进行了能量传递。图9中，轮胎摆振的动能随转向机构角刚度的增大而减小，并且在刚度为16 400 N·m/rad时发生突降。所以设计时可适当增大转向机构角刚度以吸收更多的前轮振动能量从而抑制摆振。

图8　能量时间历程曲线Fig.8 Time history of energy

图9　前轮动能变化趋势Fig.9 Change trends of kinetic energy of front wheel

图10所示为考虑左右梯形臂运动副间隙动力学耦合作用时的左轮摆角幅值随车速的分岔特性，从中看出系统会产生跳跃现象。对跳跃前后一系列车速下的摆振动力学响应进行分析，发现跳跃前的运动形态为单周期运动，如图11所示；跳跃后的运动形态为周期3运动，如图12所示。随着车速进一步增大至70 km/h，摆振幅值达到最大，此时系统做拟周期运动，如图13所示。可见系统的运动形态会随着车速的变化发生改变。系统响应由跳跃前的单周期变为3周期，然后3周期运动的周期解失稳，发生Naimark-Sacker分岔，为拟周期运动。

图10　摆振幅值分岔特性Fig.10 Bifurcation of shimmy amplitude

图11　车速v=25 km/h时的左轮摆角响应Fig.11 Dynamic response of left front wheel(v=25 km/h)

图12　车速v=30 km/h时的左轮摆角响应Fig.12 Dynamic response of left front wheel(v=30 km/h)

图13　车速v=70 km/h时的左轮摆角响应Fig.13 Dynamic response of left front wheel(v=70 km/h)

3结论

(1) 考虑不同间隙运动副之间动力学耦合作用的车辆摆振系统动力学响应会发生较大变化。同样初始条件下，由于不同间隙副之间的动力学耦合作用，车辆摆振幅值显著增大，同时系统响应的运动形态趋于复杂，更易发生拟周期运动甚至混沌。

(2) 发生摆振时，能量在转向机构与车轮之间进行传递。两侧间隙接触力对车轮均有能量输入，会加剧摆振。

(3) 摆振系统动力学响应会随车速变化出现分岔现象。系统响应由跳跃前的单周期变为3周期，然后3周期运动的周期解失稳，发生Naimark-Sacker分岔，作拟周期运动。

参 考 文 献

[1] Demic M. Analysis of influence of design parameters on steered wheels shimmy of heavy vehicles[J]. Vehicle System Dynamics, 1996, 26(5): 343-362.

[2] Zhuravlev V Ph, Klimov D M. The causes of the shimmy phenomenon[J]. Doklady Physics, 2009, 54(10): 475-478.

[3] 管迪华，何泽民，肖田元，等. 汽车转向轮振动的研究[J].汽车工程，1984:29-40.

GUAN Di-hua, HE Ze-min, XIAO Tian-yuan,et al. Research on vehicle steering wheel vibration[J]. Automotive Engineering, 1984:29-40.

[4] 郭孔辉. 轮胎动态侧偏特性对汽车摆振的影响[J]. 汽车技术，1995(4): 1-6.

GUO Kong-hui. Influence on vehicle shimmy by dynamic characteristics of wheel tire lateral[J]. Automotive Technology, 1995(4): 1-6.

[5] Lu Jian-wei, Xin Jia-yun, Vakakis A F, et al.Influences of system parameters on dynamic behavior of the vehicle shimmy system with clearance in steering linkage[J]. Journal of Vibration Control, doi: 10.1177/1077546313483786.

[6] 张云清，陈伟，陈立平. Magic Formula轮胎模型参数辨识的一种混合优化方法[J]. 汽车工程，2007(3): 250-255.

ZHANG Yun-qing, CHEN Wei, CHEN Li-ping. A hybrid optimization on parameters identification for magic formula tire model[J]. Automotive Engineering, 2007(3): 250-255.

[7] 卢剑伟，陈昊，辛加运，等.转向传动机构间隙对车辆摆振系统动力学行为的影响分析[J].振动与冲击，2013,32(16):171-175.

LU Jian-wei,CHEN Hao,XIN Jia-yun,et al.Influence of steering linkage clearance on dynamic behavior of vehicle shimmy system[J].Journal of Vibration and Shock,2013,32(16):171-175.

基金项目：国家自然科学基金(50975071);教育部新世纪优秀人才支持计划(NCET-10-0358)及安徽省高校省级自然科学研究重大项目等资助

收稿日期：2014-07-08修改稿收到日期：2014-10-16

通信作者卢剑伟 男，博士，教授，博士生导师，1975年生

中图分类号:U461.6；TH132

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.01.012

Dynamic behavior analysis of a vehicle shimmy system considering dynamic coupling in joints with clearance

JIANG Jun-zhao, LU Jian-wei, ZHANG Hui

(School of Mechanical and Automobile Engineering, Hefei University of Technology, Hefei 230009, China)

Abstract:Dynamic coupling in joints with clearance for a steering mechanism of a vehicle has great influences on its dynamic responses. Based on analytical mechanics, a 6-DOF dynamic model for a vehicle shimmy system considering dynamic coupling in joints with clearance was established. Numerical analysis was carried out to evaluate the dynamic responses of the vehicle shimmy system. Some phenomena, such as, Naimark-Sacker bifurcation and chaos of the system were analyzed, and the mechanism of vehicle shimmy was explained in the view of energy transfer. The results provided a theoretical basis for controlling vehicle shimmy.

Key words:vehicle; shimmy; clearances; dynamic coupling

第一作者 姜俊昭 男，博士生，1987年生