含液饱和多孔波阻板的地基振动控制研究

周凤玺， 马　强， 赖远明

(1.兰州理工大学 土木工程学院，兰州　730050; 2中国科学院 寒区旱区环境与工程研究所，兰州　730000)



含液饱和多孔波阻板的地基振动控制研究

周凤玺1,2， 马强1， 赖远明2

(1.兰州理工大学 土木工程学院，兰州730050; 2中国科学院 寒区旱区环境与工程研究所，兰州730000)

摘要：基于含液饱和多孔介质中的流-固耦合作用，提出了以含液饱和多孔材料作为隔振屏障的一类新型的地基振动控制体系。考虑在弹性地基内部设置饱和多孔波阻板，基于线弹性理论和Biot多孔介质模型，采用Fourier级数展开的方法，分别建立了地基表面和内部受到条形简谐荷载作用下地基动力响应的计算列式。通过数值算例，与传统的单相固体波阻板的隔振效果进行了比较，并且分析了多孔材料波阻板中固相材料性质、孔隙率、孔隙流体性质等物理力学参数对地基隔振性能的影响规律。结果表明，相对于单相固体波阻板隔振体系，基于含液饱和多孔波阻板的地基隔振体系更加具有优越性，并且更具有可设计性。

关键词：地基振动控制；波阻板；含液饱和介质；弹性地基；条形简谐荷载

随着城镇化建设和现代工业的迅速发展，各种人工振动引起的环境污染问题日益频繁；另一方面，随着生活水平的提高，人们对生活环境和工作环境的质量要求也越来越高，环境振动的影响已经引起人们的普遍关注。环境振动及其治理已经成为岩土工程的一个研究热点问题。

地基振动由于振源位置、振源类型以及地基物理力学性质的不同而产生不同的波场特性，其振动的传播过程和衰减规律也不相同。关于地基的动力行为以及波的传播特性问题，国内外学者从荷载类型、地基特征(包括材料特性和边界条件)等多方面进行了分析并取得了一系列重要的研究成果[1-5]，然而关于地基振动的控制问题则研究较少。自Woods[6]通过一系列的现场原位试验，研究了近场主动隔振和远场被动隔振的隔振效果，提出了采用振幅衰减系数来衡量屏障隔振效果，为理论和试验研究提供了一个判断屏障隔振效果的重要参数以来，国内外学者通过试验测试对连续屏障和非连续屏障的减振隔振效果进行了一系列的研究工作[7-14]。其中，在地基中人工设置波阻板(Wave Impedance Block，WIB)来实现振动控制的隔振性能研究也取得了长足的发展。Chouw等[15]采用二维频域边界元法对波阻板主动隔振和被动隔振进行了分析，并对波阻板被动隔振与填充沟被动隔振进行了对比分析，得出了波阻板隔振效果要优于填充沟的结论。采用轴对称和反轴对称有限元法，Takemiya等[16]分析了基岩上单一土层中群桩基础激振时波阻板的隔振效果，结果表明，对于桩基础激振情况下，采用波阻板进行隔振也很有效。采用边界积分方程法，Peplow等[17]研究了二维双层地基波阻板主动隔振的隔振效果。Takemiya[18]首次提出了一种蜂窝状波阻板(Honeycomb WIB,HWIB)隔振措施，对高架铁路桩基振动HWIB隔振进行了现场试验，得到了令人满意的隔振效果。李志江等[19]通过有限元方法研究了HWIB对高速铁路引发低频振动的隔振效果，并与实体波阻块的隔振效果进行了对比。高广运等[20-21]建立了层状介质中土与结构动力相互作用的半解析边界元法模型，分析了二维和三维层状地基中波阻板的隔振效果。

含液饱和多孔介质是内部具有细观孔隙结构且孔隙中充满液体的两相材料，在岩土工程、生物工程以及传热传质等众多工程领域中有着非常广泛的应用。由于固相骨架与孔隙液体的相互作用以及两者不同的运动特性，含液饱和介质的力学行为与单相介质截然不同，有其独特的特性。自Biot[22]提出描述饱和多孔介质动力特性的基本方程以来，国内外众多学者从不同角度对多孔介质动力学问题进行了研究。由于流-固两相的相互耦合作用使得饱和多孔介质结构在振动过程中引起能量的耗散，具有类似阻尼效应[23-24]。以含液饱和多孔材料作为隔振屏障，本文提出了一类新型的波阻板地基隔振体系。考虑平面应变问题，利用Fourier级数展开的方法，研究了半平面弹性地基在表面和内部受到条形简谐荷载作用时含液饱和多孔波阻板的隔振性能，并与单相固体波阻板的隔振效果进行了比较。

1控制方程

1.1单相固体介质

各向同性的线弹性单相连续固体介质的控制方程为

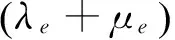
(1)

式中：λe和μe表示固体材料的Lame弹性常数；ρe为固体材料密度；ue表示位移矢量。

相应的应力位移关系为

(2)

式中：σe表示单相弹性固体中的应力张量；I为单位矩阵。

根据Helmholtz矢量分解定理，位移矢量ue可被写成如下形式

ue=φe+×ψe，·ψe=0

(3)

式中：φe和ψe分别表示单相固体的标量位移势函数和矢量位移势函数。

将式(3)代入式(2)中，整理后可得以位移势函数表示的弹性固体波动方程

(4)

1.2两相饱和多孔介质

基于Biot多孔介质理论，均质线弹性饱和多孔介质动力响应问题的控制方程为

μp2u+(μp+λp+α2M)e-

αM

(5)

αMe-M

(6)

式中：u和w分别表示多孔介质中固体骨架位移和流体的相对位移；e=·u，ζ=-·w；λp和μp为多孔介质固体骨架Lame常数；b=η/kf，η为流体黏滞系数，kf表示渗透系数；α和M为考虑二相材料压缩性的Biot参数，/Ks+n/Kf，其中K、Ks和Kf分别为固体骨架、固体颗粒和孔隙流体的体积模量；m=ρf/n表示与孔隙水的质量密度及孔隙几何特征有关的参数；ρs+nρf为混合物介质的质量密度，其中，n为孔隙率，ρs和ρf分别为固相和液相的密度。

根据Helmholtz矢量分解原理，位移矢量u和w可以用位移势函数φs，ψs，φf和ψf表示为

u=φs+×ψs，·ψs=0

(7)

w=φf+×ψf，·ψf=0

(8)

将式(7)和式(8)代入控制方程(5)和(6)，令φs=φ1+φ2，经过整理后可得[5]

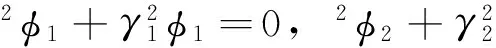
(9)

φf=δp1φ1+δp2φ2，ψf=δsψs

(10)

式中:

相应地用位移表示的应力和孔隙流体压力为

σ=(λp+α2M)(·u)I+

αM(·w)I+μe(u+u)

(11)

p=-αM(·u)+M(·w)

(12)

式中:σ和p为饱和多孔介质的总应力张量和孔隙流体压力。

2位移势函数的级数解

考虑弹性半空间受到频率为ω，幅值为q0的竖向条形简谐荷载q=q0eiωt荷载作用，问题可简化为x1x3平面内的平面应变问题。利用Fourier级数将荷载函数q和位移势函数展开为如下形式

(13)

(14)

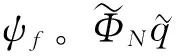
(15a)

(15b)

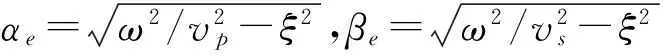
同样，将式(14)代入式(9)和式(10)，经过整理以后可得双相多孔介质的各位移势函数的通解为

Atp2δp2e-iαp2x3+Arp2δp2eiαp2x3

(16b)

(16c)

(16d)

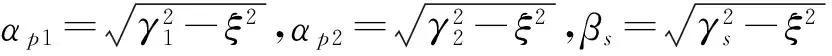
3动力荷载作用在半平面表面

考虑弹性半平面的表面受到简谐荷载q0eiωt的作用，如图1所示。厚度为hw的波阻板设置在距离地基表面深度为H处。波阻板将弹性半平面分成Ⅰ、Ⅱ两部分，图中给出了波的传播以及波幅示意图。其中，在波阻板中右侧实线表示当波阻板为两相多孔介质时波的传播特性，而左侧虚线表示当波阻板为单相弹性固体时波的传播示意。

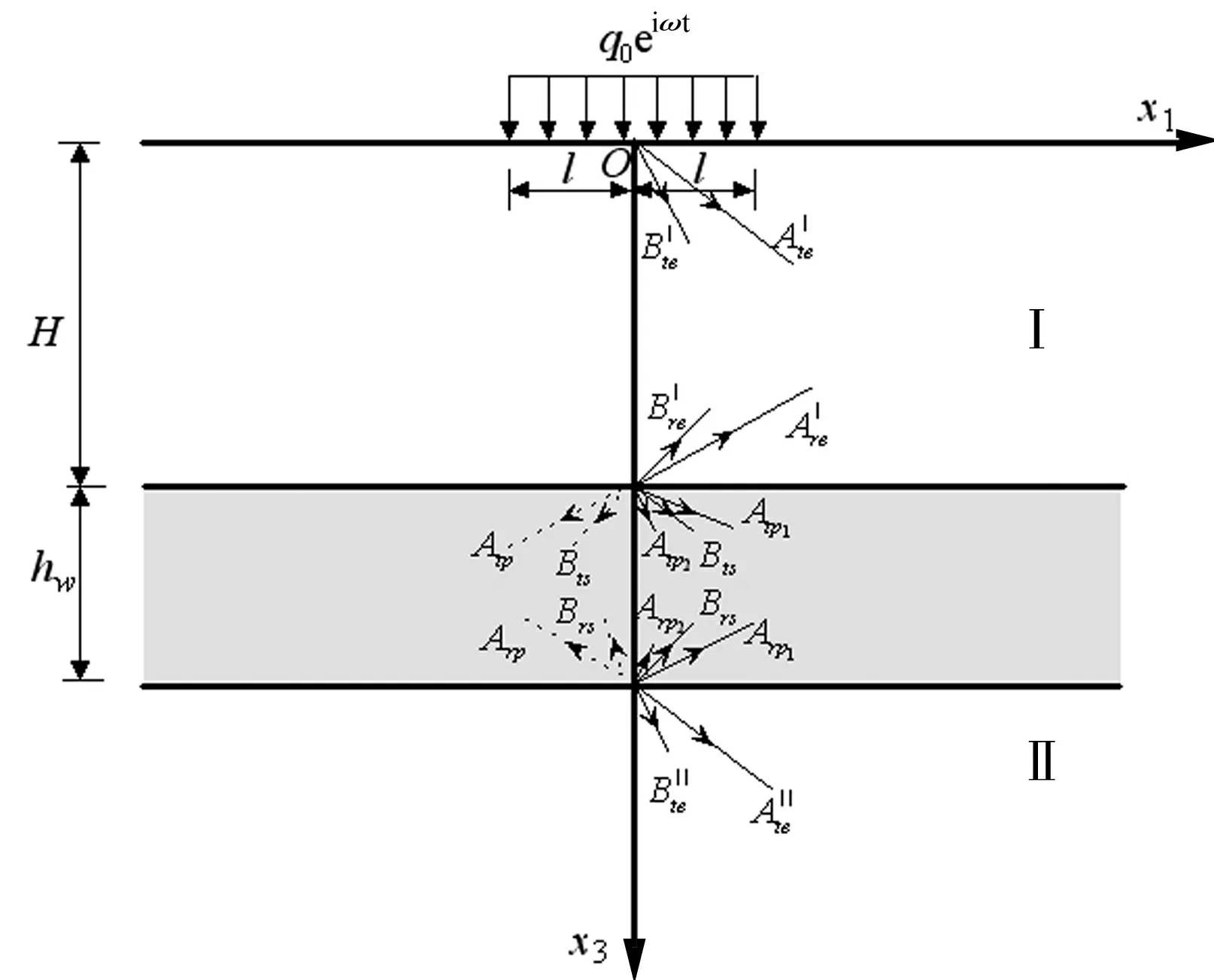
图1　荷载作用在设置有波阻板的弹性半平面表面Fig.1 The elastic half plane subjected a surface strip harmonic load

3.1地基动力响应

将式(15)代入式(2)和式(3)中，将式(16)代入式(7)、式(8)和式(11)、式(12)中，可分别得到弹性介质和多孔介质中的位移、应力等物理量的表达式。

在0≤x3≤H的区域内

(17a)

(17b)

(17c)

(17d)

在H≤x3≤H+hw的区域内

Arp2eiαp2x3)+iβs(Btse-iβsx3-Brseiβsx3)

(18a)

iαp2(Atp2e-iαp2x3-

Arp2eiαp2x3)+iξ(Btse-iβsx3+Brseiβsx3)

(18b)

w1=iξ(Atp1δp1e-iαp1x3+Arp1δp1eiαp1x3+Atp2δp2e-iαp2x3+

Arp2δp2eiαp2x3)+iβsδs(Btse-iβsx3-Brseiβsx3)

(18c)

(Atp1e-iαp1x3+Arp1eiαp1x3)+2μpξβs(Btse-iβsx3-Brseiβsx3)-

(Atp2e-iαp2x3+Arp2eiαp2x3)

(18d)

2ξαp2(Atp2e-iαp2x3-Arp2eiαp2x3)+

(18e)

如果波阻板为单相固体介质，此时在H≤x3≤H+hw的区域内式(18)退化为

iβw(Btse-iβwx3-Brseiβwx3)

(19a)

iξ(Btse-iβwx3+Brseiβwx3)

(19b)

Arpeiαwx3)+2μwξβw(Btse-iβwx3-Brseiβwx3)

(19c)

(19d)

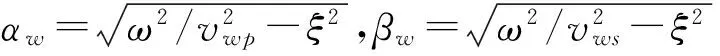
在x3≥H+hw的区域内

(20a)

(20b)

(20c)

(20d)

3.2边界条件以及界面处的连续条件

对于荷载作用在半平面表面的情形，其边界条件以及各层界面处的连续条件如下

在x3=0处

(21)

其中：ξN=Nπ/L，L表示远大于荷载宽度l的参考距离。

在x3=H处

(22)

在x3=H+hw处

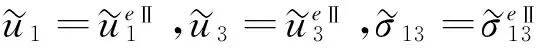
(23)

如果波阻板为单相弹性材料，在连续条件(22)和(23)变成

(24)

(25)

对于波阻板为两相多孔介质材料或单相弹性材料的情况，分别根据式(21)～式(22)或式(21)，式(24)～式(25)可得到用矩阵形式统一表示的方程组

[a]{x}={f}

(26)

式中:矩阵[a]以及矢量{x}和{f}中的各元素详见附录A。

4动力荷载作用在半平面内部

作为另一种常见的情形，考虑简谐荷载q0eiωt作用于半平面内部距波阻板底面的深度为h，如图2所示。此时，波阻板和荷载作用面将弹性半平面分成用Ⅰ、Ⅱ和Ⅲ表示的三部分。

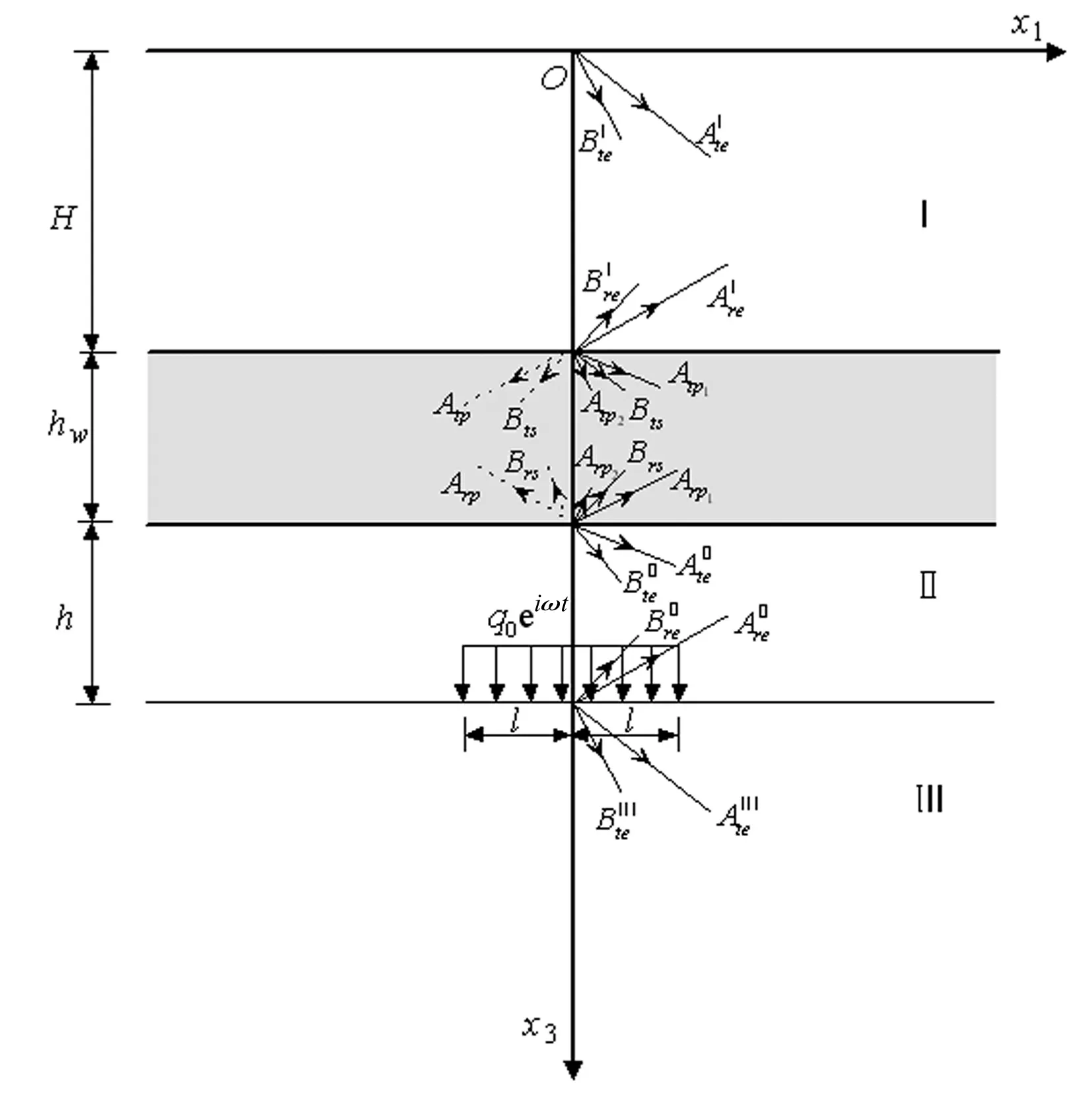
图2　荷载作用在设置有波阻板的弹性半平面内部Fig.2 The elastic half plane subjected a internal strip harmonic load

相应于对于荷载作用在半平面内部的情形，其边界条件以及各层界面处的连续条件如下

在x3=0处

(27)

对于两相多孔材料波阻板时

在x3=H处

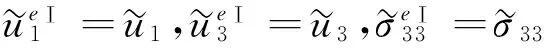
(28)

在x3=H+hw处

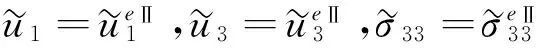
(29)

对于单相弹性材料波阻板时，式(28)和式(29)变为

在x3=H处

(30)

在x3=H+hw处

(31)

在x3=H+hw+h处

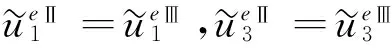
(32)

与荷载作用于地基表面的推导过程类似，结合式(27)～式(29)和式(32)或结合(27)，和式(30) ～式(32)，同样可分别得到波阻板为多孔介质材料和单相弹性材料的情形下的形式如式(26)表示的方程组，方程中的各元素详见附录B。

通过求解方程组(26)，获得各类波第N项的振幅{x}后，结合式(15)～式(20)，最终可得到弹性地基中和波阻板中任意点处的应力和位移响应。

5数值算例

5.1本文方法验证

Lamb在1904年发表了他对弹性半空间介质受力后波场分布的研究结果。从此人们把振源位于半无限介质表面或内部所产生的波的传播问题称为Lamb问题。当半无限体表面作用分布宽度为2l的均布条形荷载q0时，在条形荷载边缘下深度x3处的应力σ33的解析表达式为[25]

(33)

当该条形荷载作用在半空间内部局表面H深度时，则条形荷载边缘下某一深度x3处的应力σ33为[25]

(34)

式中：ν为材料泊松比。

为了验证本文方法的正确性，将方程组(26)可退化到无波阻板的情形，具体见附录C。计算中取均布荷载幅值q0=1 kPa，频率ω=0.01 rad/s，l=1 m，材料的弹性模量E=1×107N/m2，泊松比ν=0.3，密度ρ=1 884 kg/m3。对荷载函数q进行傅里叶级数展开，则荷载函数在波长2L内被离散成2N+1个相等的空间点，取值由0～2N，波长2L被分为相等的2N段。如果取样间隔Δx=0.1 m，相对于荷载长度2l比较小。对于实际算例来说，2N取为4 096，即2L为409.6 m[26]。分别计算了荷载作用在表面以及作用在深度H=4 m时条形荷载边缘下的应力σ33，并与解析解(33)和(34)进行了比较，如图3和图4所示。可以看出在频率很小时，与静态解答基本一致。

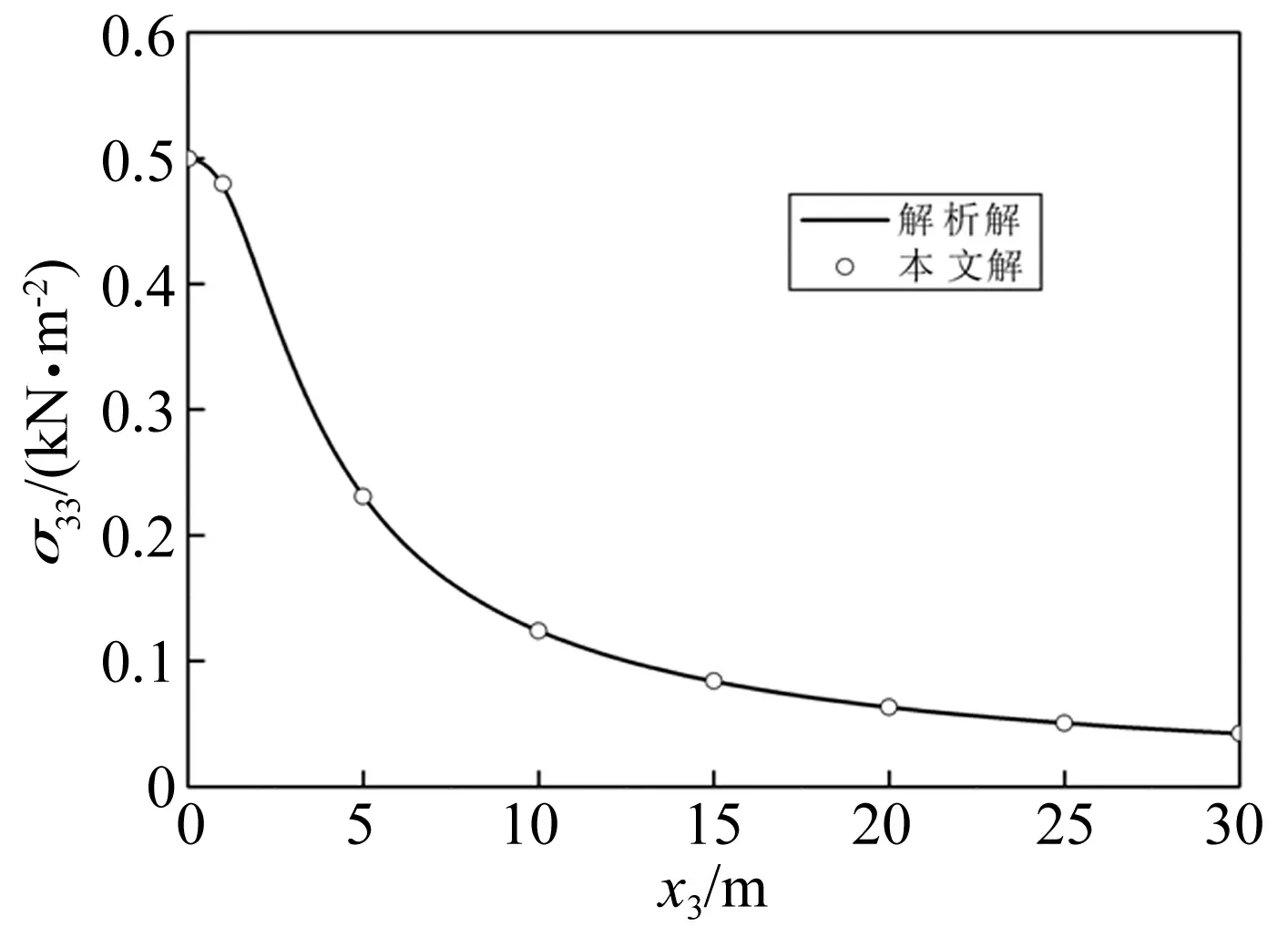
图3　条形荷载作用于表面时荷载边缘下的应力Fig.3 Thenormal stress under corner point of surface load

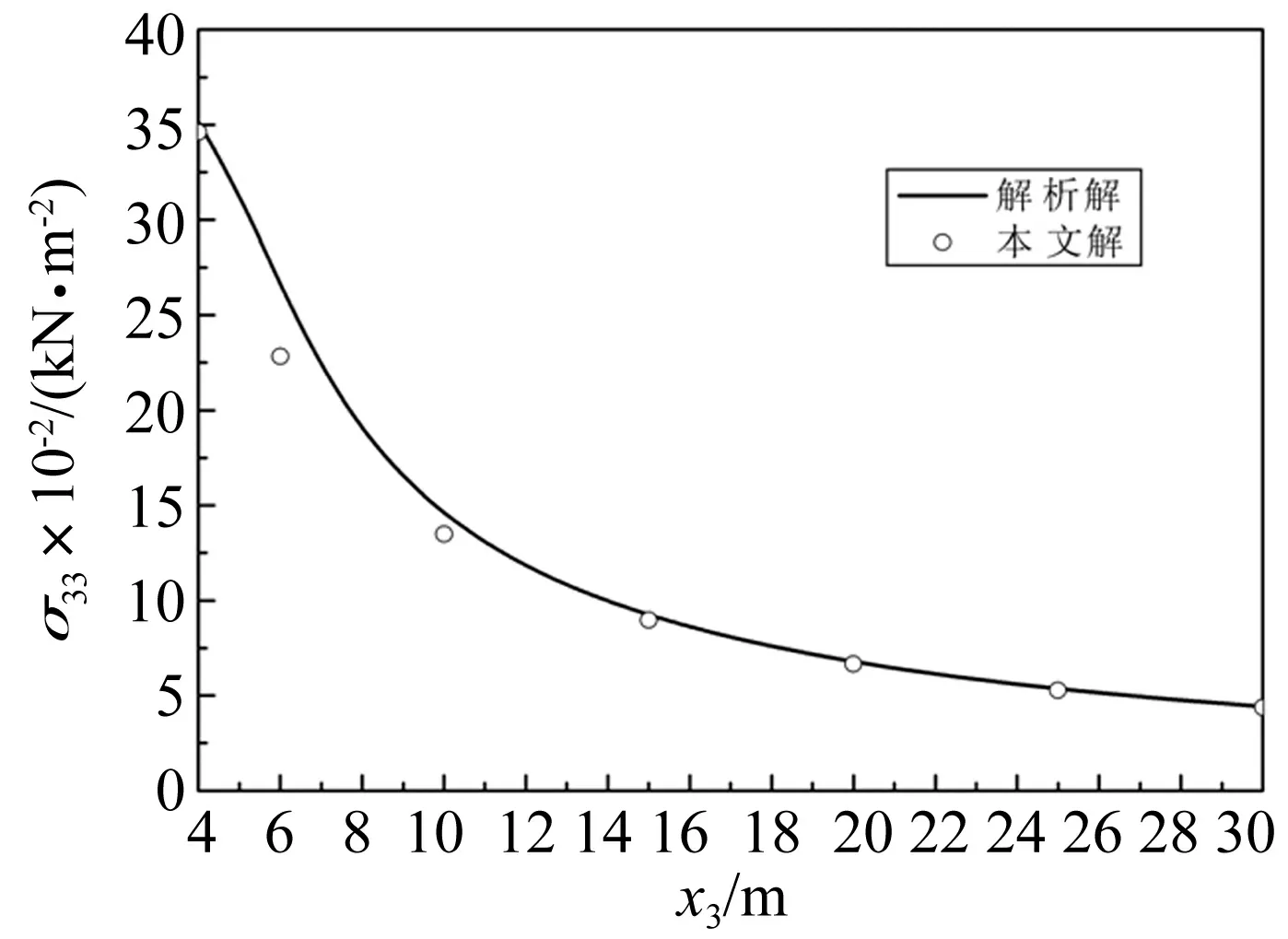
图4　条形荷载作用于内部时荷载边缘下的应力Fig.4 Thenormal stress under corner point of internal load

5.2数值分析

为了研究多孔材料波阻板对地基振动控制的效果，算例中对各种不同的波阻板，包括单相弹性波阻板、气饱和波阻板以及液饱和波阻板的减振隔振效果进行了比较分析，并对其中的一些影响因素进行了参数分析。选取弹性地基的物理力学参数如下：弹性模量Ee=9.8×107Pa，泊松比ν=0.3，密度ρe=1 884 kg/m3。不同波阻板的材料物理力学参数如表1所示。

考虑上覆土厚度H=4 m，波阻板厚度为hw=0.5 m的情形下(如图1所示)，图5～图7分别给出了简谐荷载频率为ω=5 rad/s，25 rad/s和50 rad/s，荷载幅值q0=1 kPa时，在地基内部6 m的深度处竖向位移沿水平方向的变化曲线，比较了弹性地基中未设置波阻板、设置单相固体波阻板以及含液饱和多孔波阻板三种不同情形。从图中可以看出，由于波阻板的设置改变了弹性地基中竖向位移的振动相位，并且与单相固体波阻板相比，含液饱和多孔波阻板具有更好的减振效果。

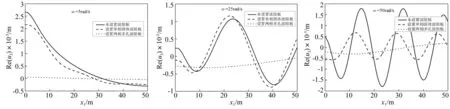
图5 ω=5rad/s时,地基内部6m处竖向位移的变化Fig.5Theverticaldisplacementat6mwithω=5rad/s图6 ω=25rad/s时,地基内部6m处竖向位移的变化Fig.6Theverticaldisplacementat6mwithω=25rad/s图7 ω=50rad/s时,地基内部6m处竖向位移的变化Fig.7Theverticaldisplacementat6mwithω=50rad/s

表1　波阻板的物理力学参数

为了分析各参数对含液饱和多孔波阻板隔振效果的影响。图8绘出了在ω=25 rad/s，n=0.27时，固相材料弹性模量从E=6.5×108Pa、1.3×109Pa、3.25×109Pa、6.5×1010Pa、6.5×1011Pa逐渐增加时，地基内部6 m的深度处竖向位移沿水平方向的变化曲线。从图中可以看出随着波阻板固体骨架弹性模量的增加，其减振效果越好，但是当增加到一定程度以后，固体骨架的弹性模量对减振性能的影响将不明显。图9给出了在ω=25 rad/s，E=6.5×108Pa的情形下，含液饱和多孔波阻板中不同孔隙率n的变化对隔振效果的影响。从图中可以明显的看出随着孔隙率的增加，其减振效果将会降低。图10为ω=25 rad/s，n=0.27时，不同流体黏滞系数的影响规律，可以看出随着孔隙中流体黏滞系数的增加，地基内部的竖向位移将越小。

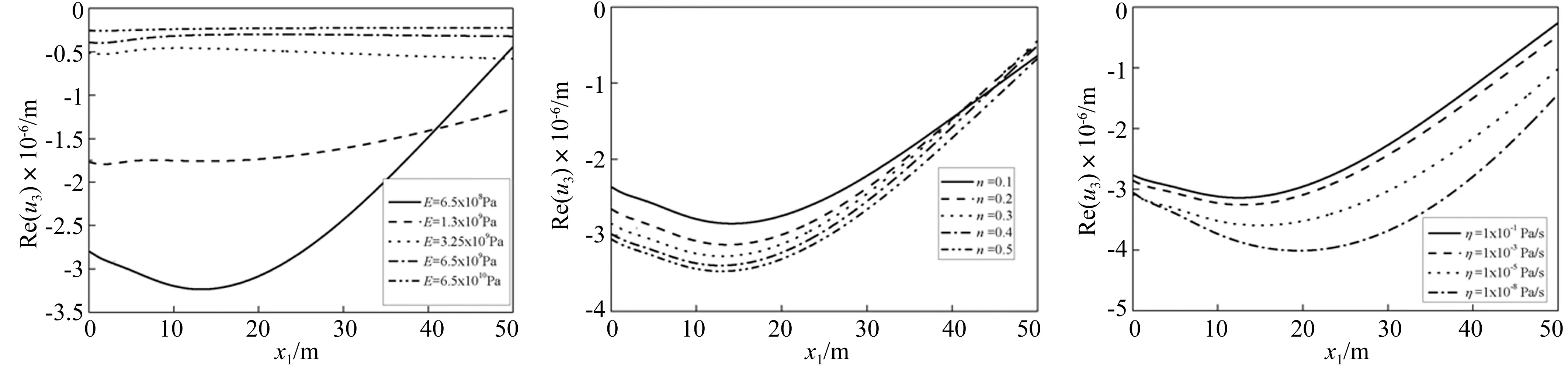
图8 含液饱和多孔波阻板固相弹性模量变化时地基内部6m处竖向位移的变化Fig.8Theeffectofsolidphaseelasticmodulus图9 含液饱和多孔波阻板孔隙比变化时地基内部6m处竖向位移的变化Fig.9Theeffectofporosity图10 含液饱和多孔波阻板流体黏滞系数变化时地基内部6m处竖向位移的变化Fig.10Theeffectofsolidfluidviscositycoefficient

与条形简谐荷载作用于地基表面类似，下面通过数值算例考察了当荷载作用于地基内部时，含液饱和多孔波阻板对地基振动的影响。算例中考虑了振源位于深度为6 m处，上覆土厚度H=4 m，波阻板厚度为hw=0.5 m的情形下(如图2所示)，图11和图12给出了不同荷载频率下，弹性地基表面处的竖向位移沿水平方向的变化曲线，比较了弹性地基中未设置波阻板、设置单相固体波阻板以及含液饱和多孔波阻板三种不同情形下竖向位移的变化曲线。从图中同样可以看出含液饱和多孔波阻板的减振效果要优于单相固体波阻板。

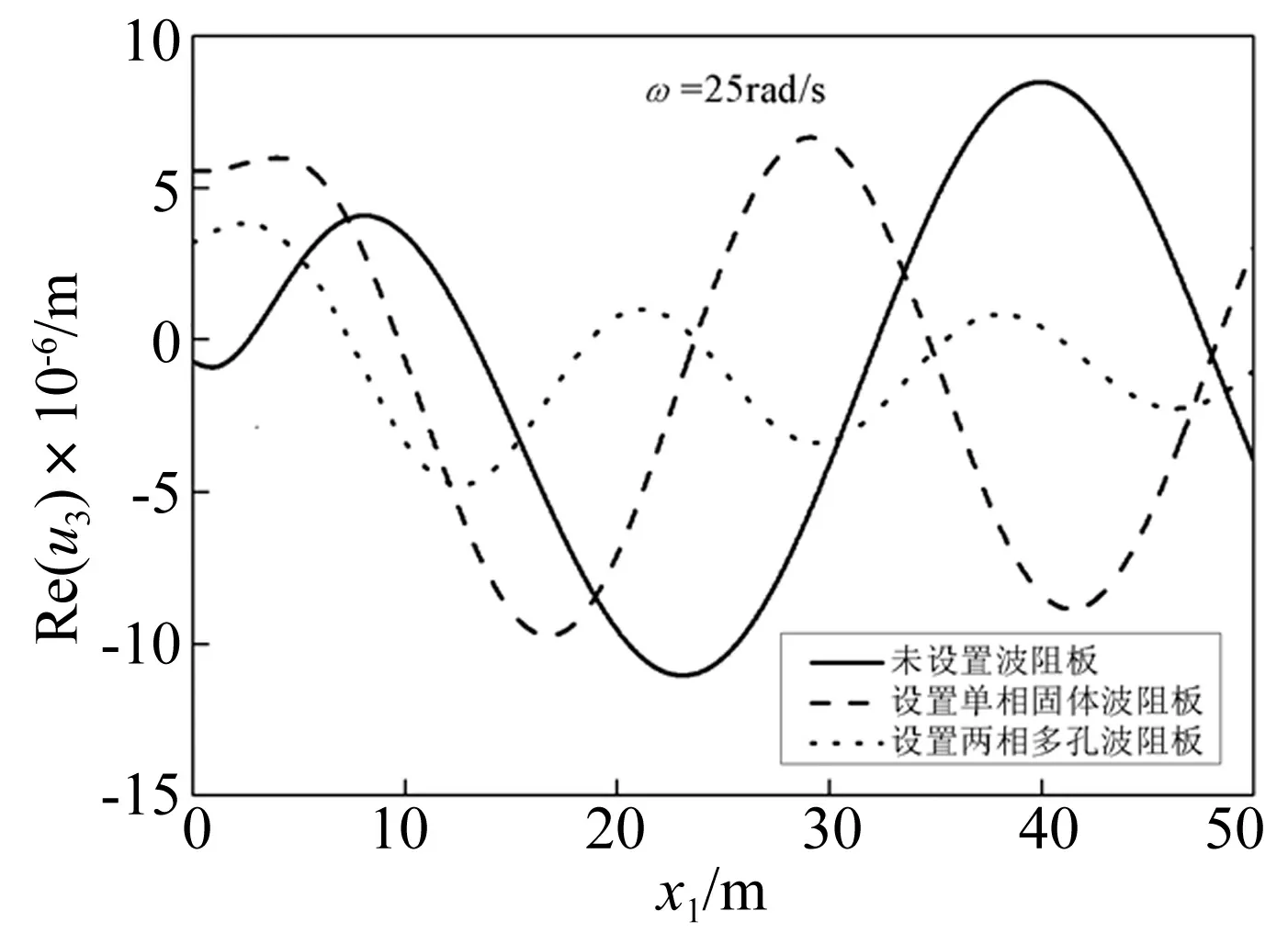
图11　ω=25 rad/s时，地基表面竖向位移的变化Fig.11 The surface vertical displacement withω=25 rad/s

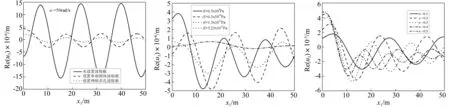
图12 ω=50rad/s时,地基表面竖向位移的变化Fig.12Thesurfaceverticaldisplacementwithω=50rad/s图13 含液饱和多孔波阻板固相弹性模量变化时地基表面竖向位移的变化Fig.13Theeffectofsolidphaseelasticmodulus图14 含液饱和多孔波阻板孔隙比变化时地基表面竖向位移的变化Fig.14Theeffectofporosity

在荷载频率为ω=5 rad/s，荷载幅值q0=1 kPa时，图13～图15分别绘出了含液饱和多孔波阻板的固相材料弹性模量E、孔隙率n以及孔隙中流体的黏滞系数η对地基表面竖向位移的影响。从图中同样可以看出含液饱和多孔波阻板的减振效果随着固相材料弹性模量和孔隙中流体的黏滞系数的增大而增加，而随着孔隙率的增大而降低。

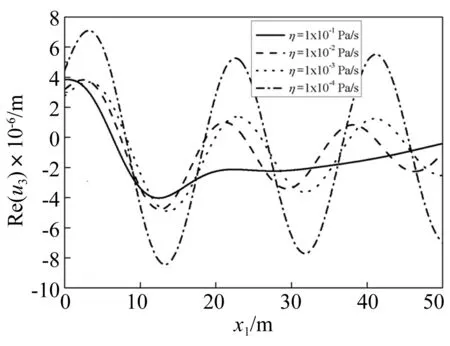
图15　含液饱和多孔波阻板流体黏滞系数变化时地基表面竖向位移的变化Fig.15 The effect of solid fluid viscosity coefficient

6结论

提出了以含液饱和多孔材料作为隔振屏障的新型地基隔振体系，基于弹性理论和Biot多孔介质模型，对含液饱和多孔波阻板的隔振性能进行了分析。分别考虑弹性地基在表面和内部受到条形简谐荷载作用，利用Fourier级数建立了地基振动问题的计算列式，分析了饱和多孔波阻板中各因素对隔振效果的影响规律。结果表明：

(1)含液饱和多孔材料的地基隔振屏障相对于单相固体波阻板是一类更具有可设计性的隔振体系。

(2)含液饱和多孔波阻板的隔振效果随着固相材料弹性模量和孔隙中流体的黏滞系数的增大而增加，而随着孔隙率的增大而降低。

参 考 文 献

[1] Sneddon I N. The stress produced by a pulse of pressure moving along the surface of a semi-infinite solid[J]. Rendiconti del Circolo Matematico di Palermo, 1952, 2: 57-62.

[2] Biot M A.Generalized theory of acoustic propagation in porous dissipative media[J]. The Journal of the Acoustical Society of America,1962a, 34: 1254-1264.

[3] Zienkiewicz O C, Chang C T, Beettss P. Drained, undrained, consolidation and dynamic behavior assumptions in soils[J]. Geotechnique, 1980, 30: 385-395.

[4] 陈远国，金波. 移动简谐荷载作用下多孔地基的动力响应[J]. 中国科学G辑, 2008, 38(3): 250-259.

CHEN Yuan-guo, JIN Bo. Dynamic response of a poroelastic stratum to moving oscillating load[J]. Science in China, Series G, 2008, 38(3): 250-259.

[5] 周凤玺, 赖远明, 宋瑞霞. 非均匀饱和土中平面波的传播特性[J]. 中国科学:技术科学, 2012, 42 (2): 131-140.

ZHOU Feng-xi, LAN Yuan-ming, SONG Rui-xia. Propagation of plane wave in non-homogenouslysaturated soils[J]. Science in China:Technological Science, 2012,42(2): 131-140.

[6] Woods R D. Screening of surface waves in soils. [J] Journal of the Soil Mechanics and Foundations Division，ASCE, 1968, 94 (4): 95l-979.

[7] Al-Hussaini T M, Ahmad S. Design of wave barriers for reduction of horizontal ground vibration[J]. Journal of Geotechnical Engineering, 199l, 117 (4): 616-636.

[8] Ahmad S，Al-Huasaini T M, Fishman K L. Investigation on active isolation of machine foundations by open trenches[J]. Journal of Geotechnical Engineering, 1996, 122: 454-461.

[9] Kattis S E, Polyzos D, Brjkos D E. Vibration isolation by a row of piles using a 3-D frequency domain BEM[J]. International Joumal for Numerical Methods in Engineering, 1999, 46 (5): 713-728.

[10] Huang Ju-hua, Xiao Xiang-zhi, Dong Xiang-huai，et al. Barrier vibration isolation to work-place vibration and its influence on uneven subsidence of pillar foundation[J]. Wuhan University Journal of Natural Sciences, 2002, 7(4): 445-450.

[11] With C, Bahrekazemi M, Bodare A. Wave barrier of lime-cement columns against train-induced ground-borne vibrations[J]. Soil Dynamics and Earthquake Engineering, 2009, 29: 1027-1033.

[12] Katsuya I, Ryota S, Tomihiro H, et al. Systematic analyses of vibration noise of a vibration isolation system for high-resolution scanning tunneling microscopes[J]. Review of Scientific Instruments, 2011, 82 (8): 702-707.

[13] 高广运, 李志毅, 邱畅. 填充沟屏障远场被动隔振三维分析[J]. 岩土力学, 2005, 26 (8): 1184-1188.

GAO Guang-yun, LI Zhi-yi, QIU Chang. Three-dimensional analysis of in-filled trench as barriers for isolating vibration in far filed[J]. Rock and Soil Mechanics, 2005, 26 (8): 1184-1188.

[14] 罗锟, 雷晓燕. 新型铁路沟屏障隔振数值分析[J]. 噪声与振动控制, 2010, 30(1): 67-71.

LUO Kun, LEI Xiao-yan. Numerical analysis of railway vibration iIsolation of new style trenches[J]. Noise and Vibration Control, 2010, 30(1): 67-71.

[15] Chouw N, Le R, Schmid G. An approach to reduce foundation vibrations and soil waves using dynamic transmitting behavior of a soil layer[J]. Bauingenieur, 1991, 66: 215-221.

[16] Takemiya H，Fujiwara A, Wave propagation/impediment in a stratum and wave impeding block (WIB) measumd for SSI response reduction[J]. Soil Dynamics and Earthquake Engineering, 1994, 13: 49-61.

[17] Peplow A T, Jones C J C, Petyt M. Surface vibration propagation over a layered elastic half-space with an inclusion[J]. Applied Acoustics, 1999, 56:283-296.

[18] Takemiya H. Field vibration mitigation by honeycomb WIB for pile foundations of a high-speed train viaduct[J]. Soil Dynamics and Earthquake Engineering, 2004, 24: 69-87.

[19] 李志江, 何锃, 谭燕, 等. HWIB用于高速铁路引发低频振动的隔振分析[J]. 华中科技大学:自然自然科学版, 2011,39 (3): 34-38.

LI Zhi-jiang, HE Cheng, TAN Yan. Isolation analysis of low-frequency vibration from high speed railway by using HWIB[J]. Journal of . Huazhong University of Science and Technology:Nature Science Edition, 2011,39 (3): 34-38.

[20] 高广运, 李伟. 二维地基波阻板隔振分析[J]. 地震工程与工程振动, 2005, 24 (2): 130-135.

GAO Guang-yun, LI Wei. 2-D analysis of ground vibration isolation using wave impeding block[J]. Earthquake Engineering and Engineering Vibration, 2005, 24 (2): 130-135.

[21] 高广运, 张博, 李伟. 层状和竖向非均匀地基中水平-摇摆耦合激振波阻板三维隔振分析[J]. 岩土力学, 2012, 2: 349-353.

GAO Guang-yun, ZHANG bo, LI Wei. 3D analysis of vibration isolation using wave impeding block in layered and vertical heterogeneous foundation under horizontal-rocking coupled excitation[J]. Rock and Soil Mechanics, 2012, 2: 349-353.

[22] Biot M A. Theory of propagation of elastic waves in a fluid-saturated porous solid I: Low-frequency range[J]. The Journal of the Acoustical Society of America, 1956, 28: 168-178.

[23] Wen P H. The analytical solutions of incompressible saturated poroelastic circular mindlin’s plate[J]. Journal of Applied Mechanics,2012, 79 (5):1-7.

[24] 杨骁, 吕新华. 饱和多孔弹性Timoshenko梁的大挠度分析[J]. 固体力学学报, 2012, 33 (1): 103-111.

YANG Xiao, LÜ Xin-hua. Large deflection analysis of a saturated poroelastic Timoshenko beam[J]. Chinese Journal of Solid Mechnics, 2012, 33 (1): 103-111.

[25] 袁聚云，赵锡宏. 竖向均布荷载作用在地基内部时的土中应力公式[J]. 上海力学， 1995, 16(3): 213-222.

YUAN Ju-yun, ZHAO Xi-hong. Formulas for the calculation ofstresses in soil subjecting to distributed loading beneath the surface of the ground[J]. Shanghai Mechnics, 1995, 16(3): 213-222.

[26] 左迎辉, 徐长节, 蔡袁强. 移动荷载下下卧基岩Gibson地基的动力响应[J]. 振动工程学报, 2005,18(3):351-354.

ZUO Ying-hui, XU Chang-jie, CAI Yuan-qiang. Dynamic analysis of Gibson soil medium on bedrock under moving load[J]. Journal of Vibration Engineering,2005,18(3):351-354.

附录A荷载作用于弹性地基表面

A.1设置含液饱和多孔材料波阻板时，方程组(26)的表达式为

(26)

矩阵[a]中的非零元素为

a14=-2μeξβe，a21=2μeξαe，a22=-2μeξαe，

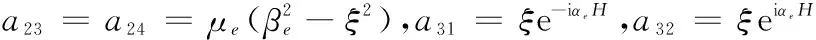
a33=βee-iβeH，a34=-βeeiβeH，a35=a36=a37=a38=-ξ，

a39=-βs，a310=βs，a41=-αee-iαeH，a42=αeeiαeH，

a43=ξe-iβeH，a44=ξeiβeH，a45=αp1，a46=-αp1，

a47=αp2，a48=-αp2，a49=a410=-ξ，

a54=-2μeξβeeiβeH，

a59=-2μpξβs，a510=2μpξβs，a61=2μeξαee-iαeH，

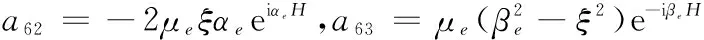
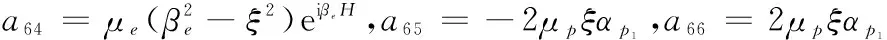
a67=-2μpξαp2，a68=2μpξαp2，

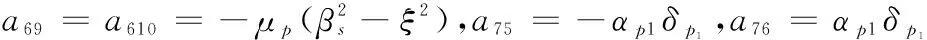
a77=-αp2δp2，a78=αp2δp2，a79=a710=ξδs，

a85=ξe-iαp1hw，a86=ξeiαp1hw，a87=ξe-iαp2hw，a88=ξeiαp2hw，

a89=βse-iβshw，a810=-βseiβshw，a811=-ξ，a812=-βe，

a95=-αp1e-iαp1hw，a96=αp1eiαp1hw，a97=-αp2e-iαp2hw，

a98=αp2eiαp2hw，a99=ξe-iβshw，a910=ξeiβshw，a911=αe，

a912=-ξ，

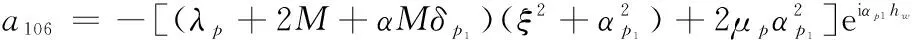
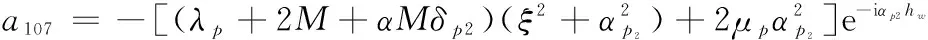
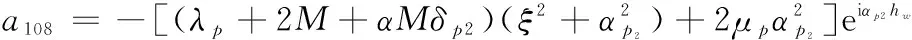
a109=2μpξβse-iβshw，a1010=2μpξβseiβshw，

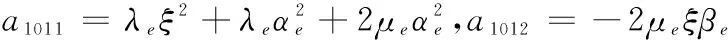
a115=2μpξαp1e-iαp1hw，a116=-2μpξαp1eiαp1hw，

a117=2μpξαp2e-iαp2h7，a118=-2μpξαp2eiαp2hw，

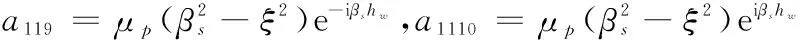
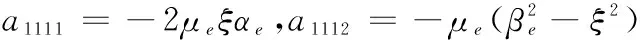
a125=-αp1δp1e-iαp1hw，a126=αp1δp1eiαp1hw，

a127=-αp2δp2e-iαp2hw，a128=αp2δp2Arp2eiαp2hw，

a129=ξδse-iβshw，a1210=ξδseiβshw

A.2设置单相弹性固体材料波阻板时，方程组(26)的表达式为

(26)

矩阵[a]中的非零元素为

a14=-2μeξβe

a31=ξe-iαeH，a32=ξeiαeH，a33=βee-iβeH，a34=-βeeiβeH，

a35=a36=-ξ，a37=-βw，a38=βw，a41=-αee-iαeH，

a42=αeeiαeH，a43=ξe-iβeH，a44=ξeiβeH，a45=αw，

a46=-αw，a47=a48=-ξ，

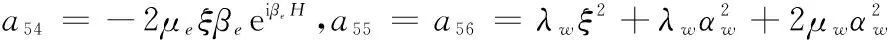
a57=-2μwξβw，a58=2μwξβw，a61=2μeξαee-iαeH，

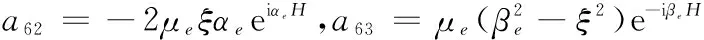
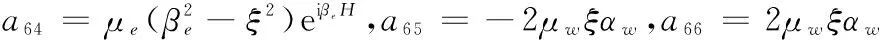
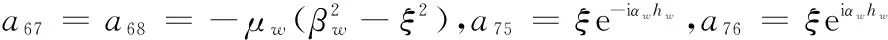
a77=βwe-iβwhw，a78=-βweiβwhw，a79=-ξ，a710=-βe，

a85=-αwe-iαwhw，a86=αweiαwhw，a87=ξe-iβwhw，

a88=ξeiβwhw，a89=αe，a810=-ξ，

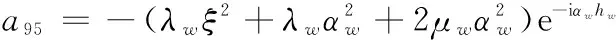
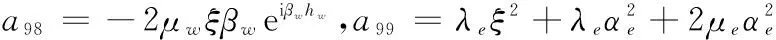
a910=-2μeξβe，a105=2μwξαwe-iαwhw，

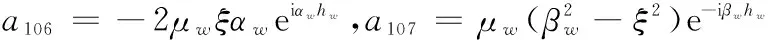
附录B荷载作用于弹性地基内部

B.1设置含液饱和多孔材料波阻板时，方程组(26)的表达式为

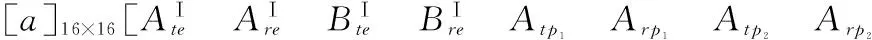
矩阵[a]中的非零元素为

a14=-2μeξβe，a21=2μeξαe，a22=-2μeξαe，

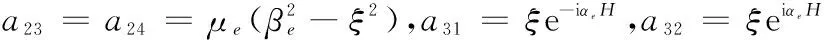
a33=βee-iβeH，a34=-βeeiβeH，a35=a36=a37=a38=-ξ，

a39=-βs，a310=βs，a41=-αee-iαeH，a42=αeeiαeH，

a43=ξe-iβeH，a44=ξeiβeH，a45=αp1，a46=-αp1，

a47=αp2，a48=-αp2，a49=a410=-ξ，

a54=-2μeξβeeiβeH，

a59=-2μpξβs，a510=2μpξβs，a61=2μeξαee-iαeH，

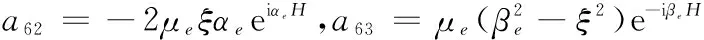
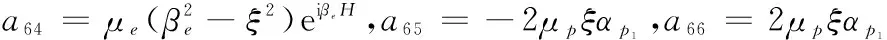
a67=-2μpξαp2，a68=2μpξαp2，

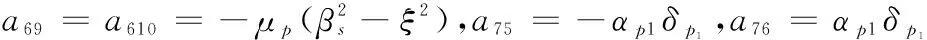
a77=-αp2δp2，a78=αp2δp2，a79=a710=ξδs，

a85=ξe-iαp1hw，a86=ξeiαp1hw，a87=ξe-iαp2hw，a88=ξeiαp2hw，

a89=βse-iβshw，a810=-βseiβshw，a811=a812=-ξ，

a813=-βe，a814=βe，a95=-αp1e-iαp1hw，a96=αp1eiαp1hw，

a97=-αp2e-iαp2hw，a98=αp2eiαp2hw，a99=ξe-iβshw，

a910=ξeiβshw，a911=αe，a912=-αe，a913=a914=-ξ，

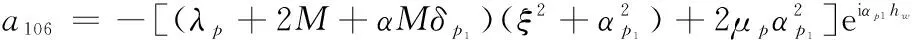
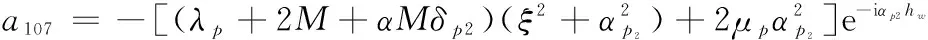
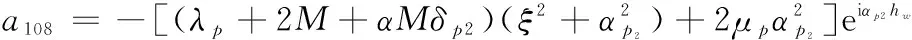
a109=2μpξβse-iβshw，a1010=-2μpξβseiβshw，

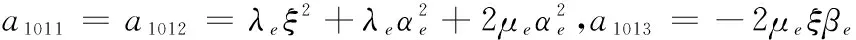
a1014=2μeξβe，a115=2μpξαp1e-iαp1hw，

a116=-2μpξαp1eiαp1hw，a117=2μpξαp2e-iαp2hw，

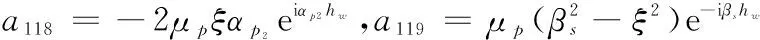
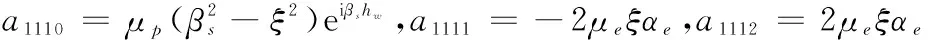
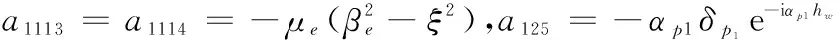
a126=αp1δp1eiαp1hw，a127=-αp2δp2e-iαp2hw，

a128=αp2δp2Arp2eiαp2hw，a129=ξδse-iβshw，a1210=ξδseiβshw，

a1311=ξe-iαeh，a1312=ξeiαeh，a1313=βee-iβeh，

a1314=-βeeiβeh，a1315=-ξ，a1316=-βe，a1411=-αee-iαeh，

a1412=αeeiαeh，a1413=ξe-iβeh，a1414=ξeiβeh，a1415=αe，

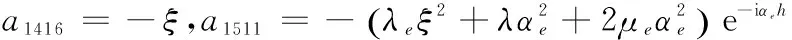
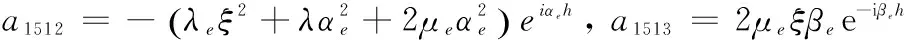
a1516=2μeξβe，a1611=2ξαee-iαeh，a1612=-2ξαeeiαeh，

B.2设置单相弹性固体材料波阻板时，方程组(26)的表达式为

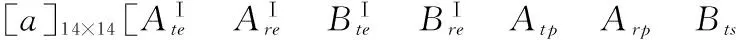
(26)

矩阵[a]中的非零元素为

a14=-2μeξβe，a21=2μeξαe，a22=-2μeξαe，

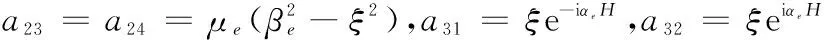
a33=βee-iβeH，a34=-βeeiβeH，a35=a36=-ξ，a37=-βw，

a38=βw，a41=-αee-iαeH，a42=αeeiαeH，a43=ξe-iβeH，

a44=ξeiβeH，a45=αw，a46=-αw，a47=a48=-ξ，

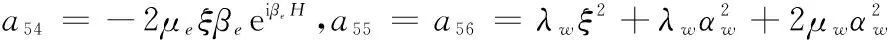
a57=-2μwξβw，a58=2μwξβw，a61=2μeξαee-iαeH，

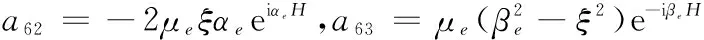
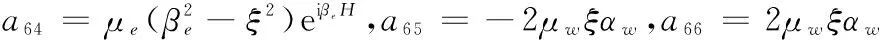
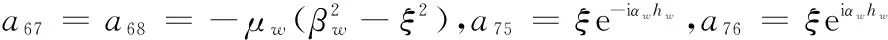
a77=βwe-iβwhw，a78=-βweiβwhw，a79=a710=-ξ，

a711=-βe，a712=βe，a85=-αwe-iαwhw，a86=αweiαwhw，

a87=ξe-iβwhw，a88=ξeiβwhw，a89=αe，a810=-αe，

a911=-2μeξβe，a912=2μeξβe，a105=2μwξαwe-iαwhw，

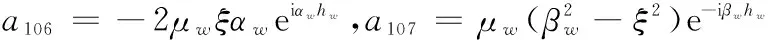
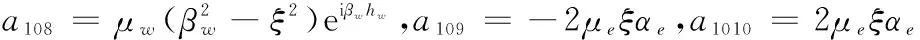
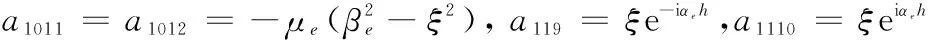
a1111=βee-iβeh，a1112=-βeeiβeh，a1113=-ξ，a1114=-βe，

a129=-αee-iαeh，a1210=αeeiαeh，a1211=ξe-iβeh，

a1212=ξeiβeh，a1213=αe，a1214=-ξ，

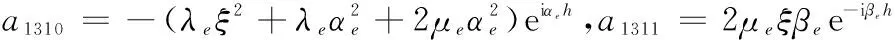
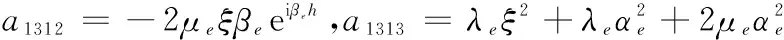
a1314=2μeξβe，a149=2ξαee-iαeh，a1410=-2ξαeeiαeh，

附录C不设置波阻板的弹性地基

C.1荷载作用于弹性地基表面时，方程组(26)的表达式为

(26)

矩阵[a]中的非零元素为

C.2荷载作用于弹性地基内部时，方程组(26)的表达式为

(26)

矩阵[a]中的非零元素为

a14=-2μeξβe，a21=2μeξαe，a22=-2μeξαe，

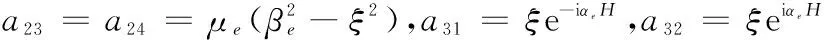
a33=βee-iβeH，a34=-βeeiβeH，a35=-ξ，a36=-βe，

a41=-αee-iαeH，a42=αeeiαeH，a43=ξe-iβeH，a44=ξeiβeH，

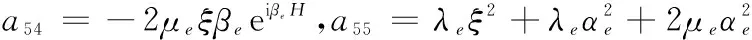
a56=-2μeξβe，a61=2μeξαee-iαeH，a62=-2μeξαeeiαeH，

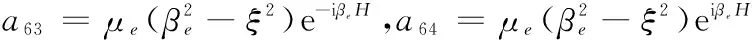
基金项目：国家自然科学基金(11162008，51368038);甘肃省高等学校基本科研业务费专项(1104ZTC140);甘肃省教育厅研究生导师基金(1103-07)资助项目

收稿日期：2014-10-10修改稿收到日期：2015-01-13

中图分类号:O324

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.01.017

Ground vibration control with fluid-saturated porous wave impeding blocks

ZHOU Feng-xi1,2, MA Qiang1, LAI Yuan-ming2

(1. School of Civil Engineering, Lanzhou University of Technology, Lanzhou 730050, China; 2. Cold and Arid Regions Environmental and Engineering Research Institute, Chinese Academy of Sciences, Lanzhou 730000, China)

Abstract:Besed on the fluid-soilid coupling in fluid-saturated porous media, a new type of foundation vibration isolation system was proposed. The fluid-saturated porous wave impeding blocks were set in an elastic foundation subjected to surface and internal strip harmonic loads. The Fouier sevies expansion method was used to build the calculation formulas of the foundation’s dynamic responses to surface and internal strip harmonic loads with the lineat elastic theory and Biot’s model. With numerical examples, the vibration isolation effect was compared to that with conventional single phase solid wave impeding block, and the influences of parameters of fluid-saturated porous material including properties of solid phase, porosity, and properties of pore fluid on the foundation’s vibration isolation performance were analyzed. The results showed that compared with the single phase solid impeding block vibration isolation sytem, the fluid-saturated porous wave impeding block vibration isolation system has more advantages and designabilities.

Key words:ground vibration control; wave impeding block; fluid saturated porous media; elastic foundation; strip harmonic load

第一作者 周凤玺 男，博士，副教授，博士生导师，1979年生