基于多分辨率奇异值分解的表面滤波方法
吴 芬 黄美发 陈磊磊 吴常林
桂林电子科技大学,桂林,541004
基于多分辨率奇异值分解的表面滤波方法
吴芬黄美发陈磊磊吴常林
桂林电子科技大学,桂林,541004
摘要:针对目前表面滤波方法中存在边界效应、缺乏多尺度性和最优小波函数选择等问题,在一维多分辨率奇异值分解(MSVD)的基础上,构造出二维MSVD,并提出基于MSVD的表面滤波方法。该方法具有多尺度性,不存在边界效应,并且不需要选择小波函数。仿真实验和实测表面数据表明,该方法与目前表面滤波方法的滤波效果相一致,适用于表面工程的评定。
关键词:表面形貌;多分辨率; 奇异值分解;表面滤波
0引言
表面形貌是指零件在加工过程中残留下来的微观几何形态,可用粗糙度、波纹度、形状误差等来表征。表面形貌客观地反映了表面生成机制,影响工程表面的功能特性[1]。为了有效地分离粗糙度、波纹度、形状误差等表面形貌特征,国内外许多学者对表面滤波技术进行了深入研究[2-3]。目前,表面滤波的方法主要有多项式拟合法、2RC滤波法、高斯滤波法、稳健高斯回归滤波法、样条滤波法和小波滤波法等。多项式拟合法能保证数学处理速度,但受函数形式和多项式次数的制约,其拟合精度有限;2RC滤波器能有效分离出高频和低频部分,但存在非线性相移的缺陷;高斯滤波法能有效分离表面成分且无相移,但存在边界效应和稳健性差的问题;稳健高斯回归滤波法解决了高斯滤波法存在的边界效应和稳健性差的问题[4];样条滤波法能有效提取大曲率曲线且没有边界效应,但其频率传输特性较差[5-7]。上述滤波法都缺乏多尺度性能,小波滤波法则具有多尺度性能但存在最优小波函数选择的问题[8]。针对目前表面滤波法所存在的问题,本文提出了一种基于多分辨率奇异值分解(MSVD)的表面滤波方法。该方法不存在边界效应和最优小波函数选择的问题,并且具有多尺度性。
1一维多分辨率奇异值分解原理
对于任何一维信号X=(x1,x2,…,xN),构造矩阵
(1)
对矩阵H进行奇异值分解[9](singular value decomposition,SVD)得到:
(2)

Aj=(aj,(1,1),(La1+La2)/2,aj,(2,N-1))
(3)
Dj=(dj,(1,1),(Ld1+Ld2)/2,dj,(2,N-1))
(4)
La1=(aj,(1,2),aj,(1,3),…,aj,(1,N-1))
La2=(aj,(2,1),aj,(2,2),…,aj,(2,N-2))
Ld1=(dj,(1,2),dj,(1,3),…,dj,(1,N-1))
Ld2=(dj,(2,1),dj,(2,2),…,dj,(2,N-2))
一维MSVD递推分解方式如图1所示[10]。
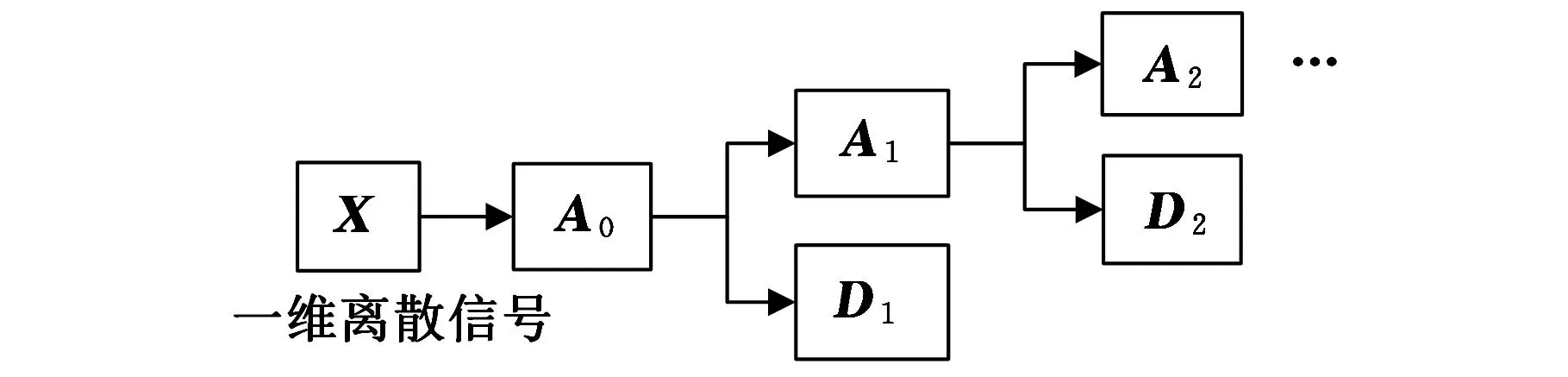
图1 一维MSVD递推分解方式
其中,Aj→Aj+1、Dj+1算法如图2所示。
由式(2)~式(4)可知:Aj=Aj+1+Dj+1,Aj和Aj+1都为N维向量,所以一维MSVD不会存在边界效应。对一维离散信号进行MSVD可知,MSVD与小波分析具有一定的差别,小波分析的分解层数是有限的,而MSVD不受分解层数的限制。文献[11]证明了{Dj}构成近似公比为0.5的等比数列,所以{Aj}是收敛的,则信号通过SVD迭代分解最终得到的结果是稳定的。

图2 Aj→Aj+1、Dj+1分解算法
2二维多分辨率奇异值分解的构造
根据一维MSVD分析理论,本文结合二维小波分析中Mallat算法来构造二维MSVD,其算法如图3所示。其中,Ajx为对矩阵Aj进行行SVD分解得到的主体成分,Djx为对矩阵Aj进行行SVD分解得到的细节成分,AjxAjy为对矩阵Ajx进行列SVD分解得到的主体成分,AjxDjy为对矩阵Ajx进行列SVD分解得到的细节成分,DjxAjy为对矩阵Djx进行列SVD分解得到的主体成分,DjxDjy为对矩阵Djx进行列SVD分解得到的细节成分。

图3 二维MSVD递推分解方式
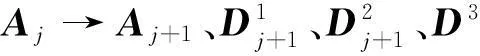
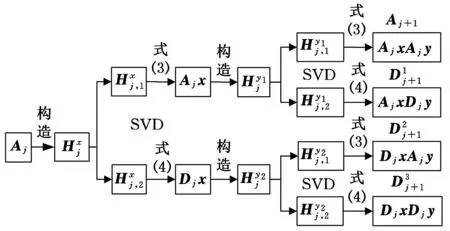
图分解算法
令
式中,M为二维离散信号的行数;N为二维离散信号的列数。

其中,int()为向下取整函数。且i=1,2,…,2M;k=1,2,…,N-1。

令
令
其中,i=1,2,…,2M;k=1,2,…,N-1。
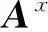
i=1,2,…,M-1;k=1,2,…,2N
分别令
其中,i=1,2,…,M-1;k=1,2,…,2N。
i=1,2,…,M-1;k=1,2,…,2N
分别令
其中,i=1,2,…,M-1;k=1,2,…,2N。
由式(2)~式(4)和图3、图4可知:
(5)
由对一维离散信号的MSVD分解结果可知,一维离散信号通过SVD迭代分解最终得到的结果是稳定的,且不存在边界效应。二维离散信号的SVD迭代分解实质上是通过行分解和列分解迭代的形式进行的,因此二维离散信号MSVD最终得到的结果是稳定的,且不存在边界效应。
3基于MSVD的表面滤波法
3.1表面形貌滤波的MSVD模型
令z(x)为二维表面轮廓信号,z1(x)为二维表面形状误差,z2(x)为二维表面波纹度,z3(x)为二维表面粗糙度; z(x,y)为三维表面轮廓信号,z1(x,y)为三维表面形状误差,z2(x,y)为三维表面波纹度,z3(x,y)为三维表面粗糙度。二维表面形貌滤波的MSVD模型可表示为
z1(x)+z2(x)=Aj(x)
其中,j为分解层数,z1(x)+z2(x)为表面评定基准线,Aj、Dk的求解见图2。三维表面形貌滤波的MSVD模型可表示为
z(x,y)=z1(x,y)+z2(x,y)+z3(x,y)=
z1(x,y)+z2(x,y)=Aj(x,y)
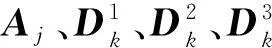
3.2MSVD模型分解层数的确定
MSVD具有多尺度性,因此可在不同尺度下对表面特征进行分离和提取。对于具有多尺度性的小波分析应用于提取表面形貌评定基准时,存在小波分解次数的确定问题,同理,MSVD用于提取表面形貌评定基准也存在分解层数确定的问题。为此,本文提出了一种基于最大临近层差值条件的方法来确定分解层数。定义二维表面和三维表面最大一维相邻层差值:
Δ(j)=max(|Aj(x)-Aj+1(x)|)
(6)
x∈(1,N)
Δ(j)=max(|Aj(x,y)-Aj+1(x,y)|)
(7)
x∈(1,N),y∈(1,N)
其中,Δ(j)为二分递推的第j层Aj与第j+1层Aj+1的最大差值。设定最大邻层差值为Δ,当j≥k时,满足Δ(j)≤Δ,则确定递推分解终止层数为k。因为{Aj}是收敛的,所以必然存在k,使得j≥k时,Δ(j)≤Δ。
3.3基于MSVD滤波法的计算复杂度
设一维测量信号为X1×N,T11、T12、T13分别为Aj→Hj、Hj→Hj,1和Hj,1→Aj+1的计算复杂度,k为分解层数,则一维MSVD滤波法的计算复杂度T1为
T1=k(T11+T12+T13)=k(O(N)+
O(max{22N,2N2})+O(N))=k·O(N2)

T2=k(T21+T22+T23+T24+T25+T26)=
k(4·O(MN)+O(MN2)+O(M2N))=
k·O(max{MN2,M2N})
4仿真计算和实验验证
4.1一维MSVD的实测实验
通过光切显微镜测量长方形铜块表面轮廓,该实验的数据评定长度为ln=7.5 mm,采样间隔为Δx=0.05 mm,采样点数为150,如图5所示。对该实验数据进行一维MSVD,设定迭代终止条件Δ=0.05,由图6可知分解层数可选17。
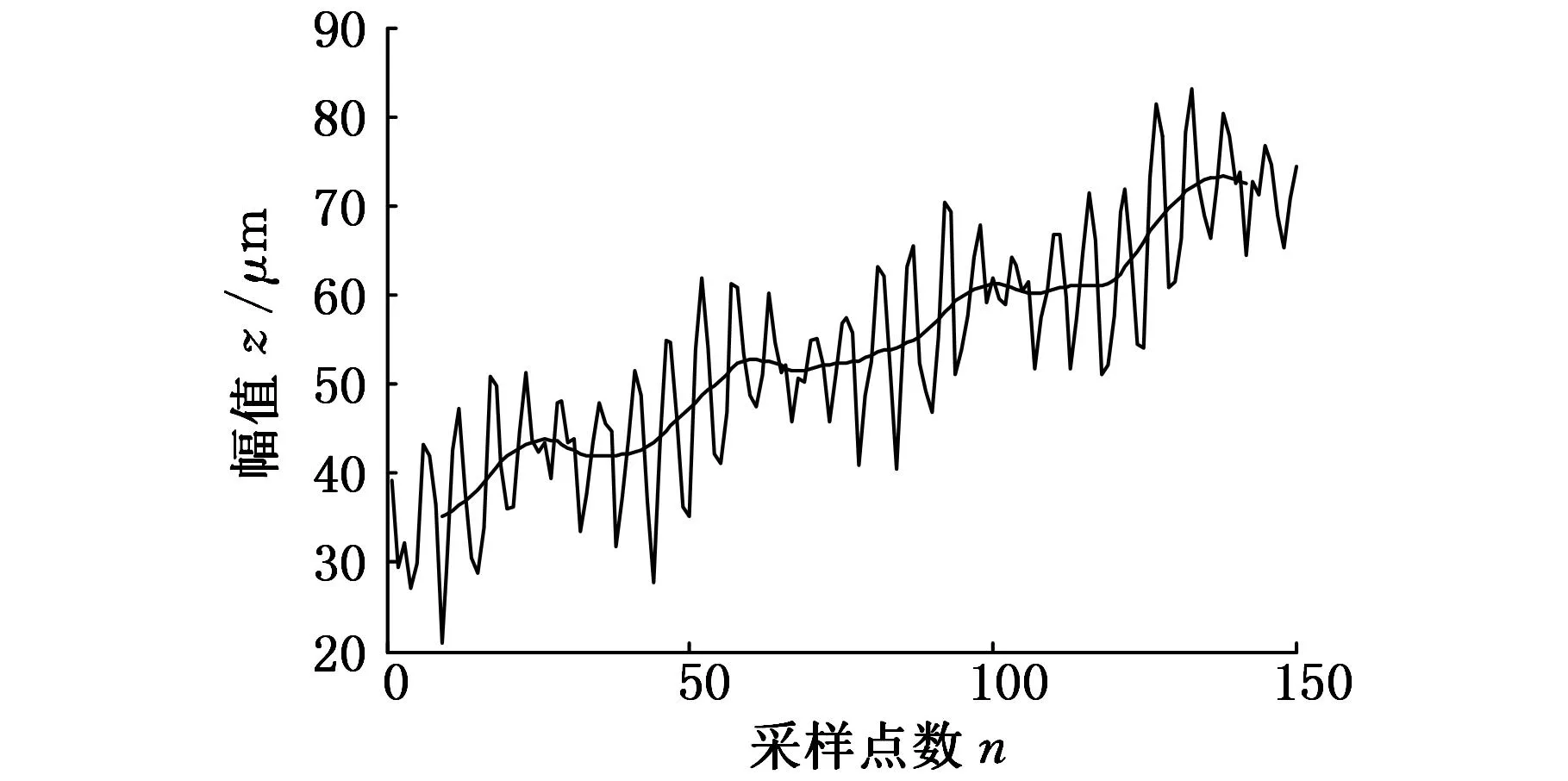
图5 高斯滤波法

图6 最大邻层差值随分解层数的变化
为了验证该方法的可行性与正确性,本文分别采用了高斯滤波法和高斯回归滤波法来提取实验数据的表面基线(图5、图7)。图8为基于一维MSVD滤波法得到的表面基线。从图5、图7、图8可知三种滤波方式得到的表面基线有较好的一致性,并且本文算法不会存在高斯滤波法所存在的边界数据丢失的问题。
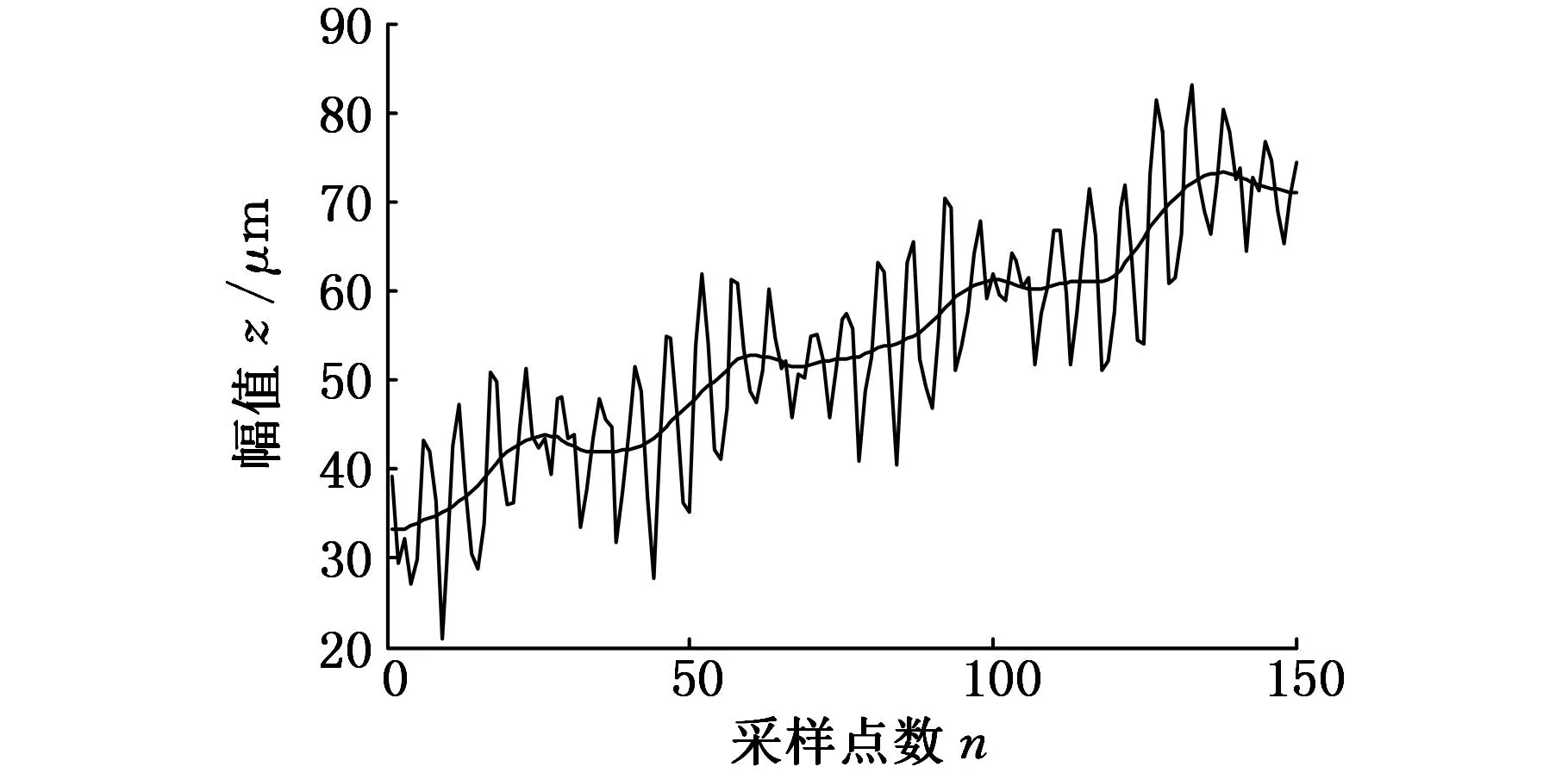
图7 高斯回归滤波法
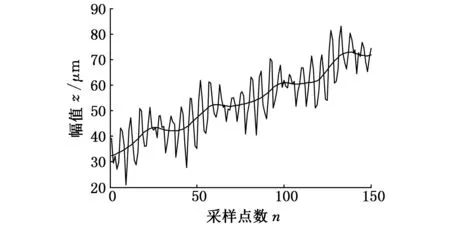
图8 一维MSVD滤波法
4.2二维MSVD仿真实验
为了说明二维MSVD对三维表面滤波法的有效性,本文以多峰函数peaks(200)作为一个采样点数为200×200的三维基准面,同时在该基准面上加白噪声作为模拟表面,如图9所示。运用基于二维MSVD滤波法对模拟表面进行滤波处理,设置迭代终止条件Δ=0.05,得到的基准面如图10所示。同时本文还分别采取了高斯回归滤波法和双树复小波滤波法来提取基准面,如图11、图12所示。

图9 模拟表面
通过对仿真数据进行对比发现:从基准面的形貌来说,三种滤波结果具有较好的一致性。不过滤波性能还是有一定的差异:采用高斯回归滤波时,得到的基准面不够自然平滑,与理想基准面有一定的差异。采用双树复小波滤波法和基于二维MSVD滤波法得到的基准面自然光滑且不存在边界效应。

图10 二维MSVD滤波法(仿真)

图11 高斯回归滤波法(仿真)

图12 双树复小波滤波法(仿真)
为了进一步评价不同滤波法对仿真信号的滤波效果,本文采用信噪比和最大误差两个评价指标来评定。其中二维信噪比RSNR为理想基准面功率和滤波后基准面的噪声功率之比:
(8)
最大误差Δmax为理想基准面与滤波后基准面的最大误差:
Δmax=max(|z(i,j)-z1(i,j)|)
(9)
其中,z为标准基准面的高度矩阵,z1为滤波后基准面的高度矩阵。通过不同滤波法提取基准面的评价指标如表1所示。
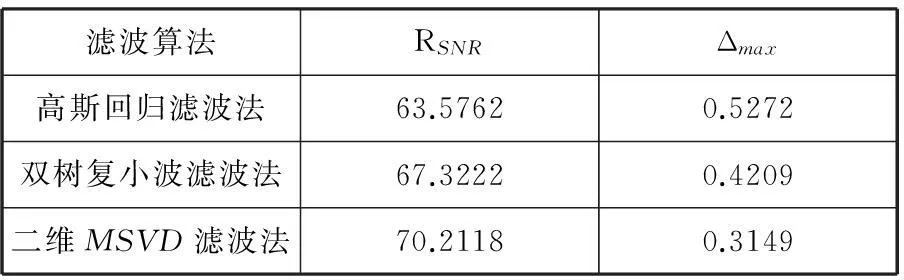
表1 滤波评价结果的对比
从表1可以看出,高斯回归滤波法信噪比最小和最大误差最大,从而评价结果最差;基于二维MSVD滤波模型得到基准面的信噪比最大并且最大误差最小,从而评价结果最优。
4.3二维MSVD实测数据分析
采用英国Taylor-Hobson公司的CCI型白光干涉式表面测量仪进行数据分析,其最小采样间距为0.078 μm,垂直分辨率为0.01 nm,实验样品为某磨削工件,采样点数为256×256,采样间距Δx=1 μm,截止波长选择为λc=80 μm,实测表面如图13所示。为了验证方法的可行性与正确性,本文分别采取高斯回归滤波法、双树复小波滤波法和二维MSVD滤波法对磨削样品进行滤波处理,结果如图14~图16所示。

图13 实测表面
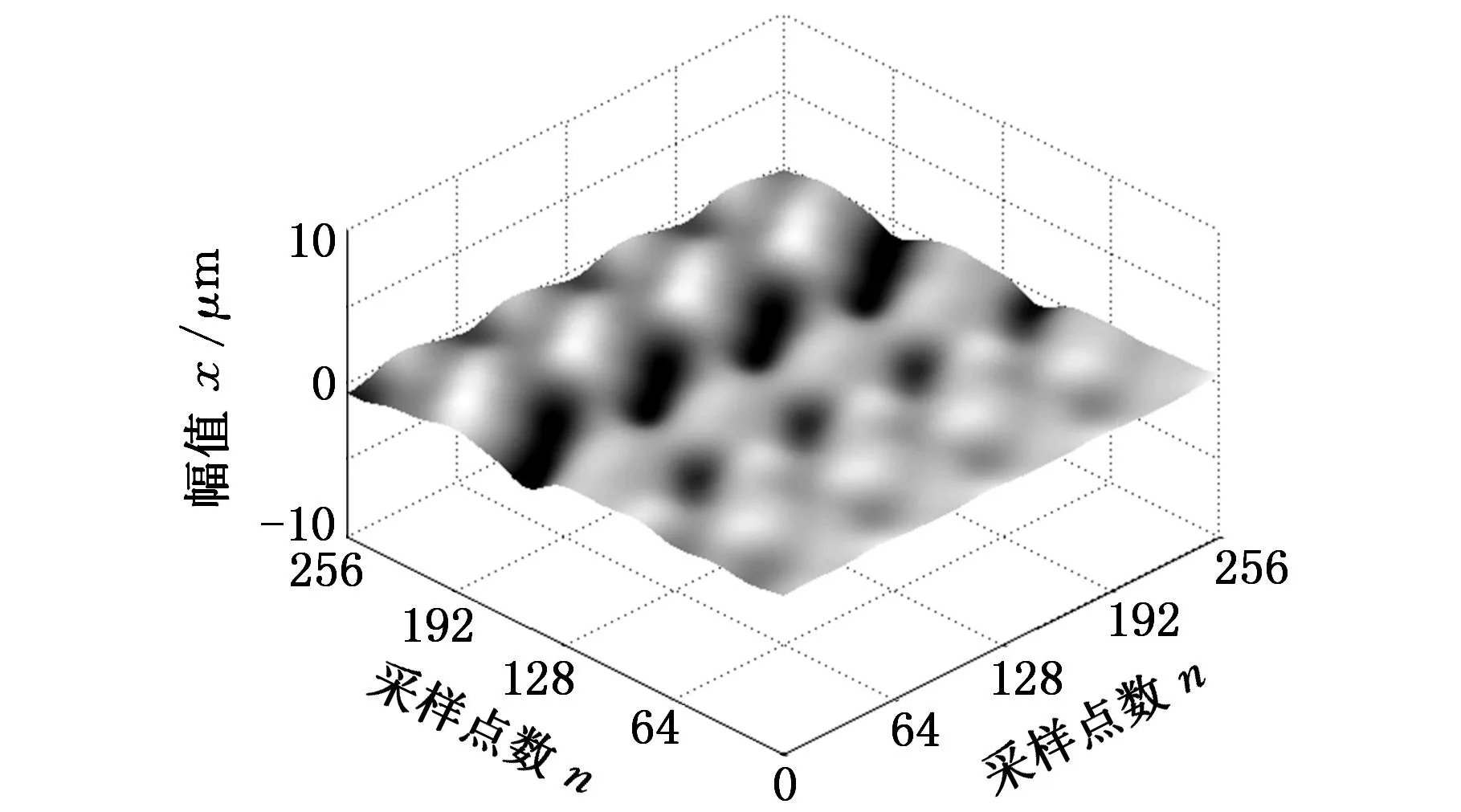
图14 高斯回归滤波法(实测)

图15 双树复小波滤波法(实测)
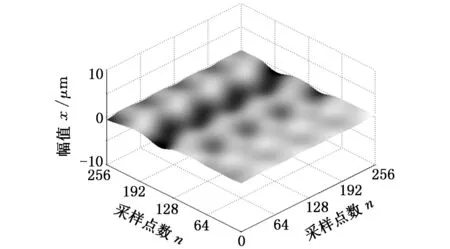
图16 二维 MSVD滤波法(实测)
由图14~图16可知,三种滤波法能有效地提取表面基准面,并且基准面的形貌具有较好的一致性。但高斯回归滤波结果受异常信号的影响有明显的凸峰和凹谷,而双树复小波滤波法和基于二维MSVD滤波法具有多尺度性,可通过选取较大尺度来抑制凸峰和凹谷,但双树复小波滤波法相邻尺度滤波结果差异性较大,并且分解尺度有限。为保证滤波结果的准确性,双树复小波分解尺度可根据截止波长或能量守恒法来确定[11-13],由采样间距和截止波长计算双树复小波分解层数为5,其滤波结果见图15。基于二维MSVD滤波法因细节成分是公比小于1的等比数列,所以相邻尺度滤波结果差异随分解尺度的增大而减小。可通过改变最大差值终止条件来微调表面基准面,这是双树复小波滤波法所不具有的。本文设置最大差值终止条件为0.05,其滤波结果如图16所示,从图16可知基于二维MSVD滤波得到基准面存在不明显凸峰和凹谷,在一定程度上能抑制异常信号的影响。
5结束语
针对表面滤波方法目前所存在的问题,提出了一种基于多分辨率奇异值分解的新的表面滤波方法,该滤波方法不存在边界效应和最优小波函数选择的问题,并且具有多尺度性。仿真实验和实测实验的结果表明,本文提出的滤波法与高斯回归滤波法、双树复小波滤波法具有较好的一致性;在上述滤波法评价结果对比中,MSVD滤波法具有良好的滤波性能,但在确定分解层数时,最大差值终止条件的设置还有待进一步研究。
参考文献:[1]Bhutan B. Tribology and Mechanics of Magnetic Storage Devices[M]. 2nd ed. New York:Springer-Velar,1996.[2]Zhang H, Yuan Y, Hua J, et al. High-order Spline Filter: Design and Application to Surface Metrology[J].Precision Engineering,2015,40:74-80.
[3]Lou S,Jiang X,Scott P J. Morphological Filters for Functional Assessment of Roundness Profiles[J].Measurement Science and Technology, 2014,25(6):065005.
[4]李惠芬.基于新一代GPS体系的表面稳健高斯滤波技术研究[D].武汉:华中科技大学,2004.
[5]Krystek M.Discrete L-spline Filtering Roundness Measurements[J]. Measurement, 1996,18(2):129-138.
[6]张浩.表面计量学中样条滤波器理论的研究[D].哈尔滨:哈尔滨工业大学,2010.
[7]张浩, 袁怡宝. 广义B样条滤波器在表面形貌测量中的应用[J].光学精密工程,2008,16(9):1722-1726.
Zhang Hao, Yuan Yibao. Application of Generalized B Spline Filter to Surface Profile Measurement[J]. Optics and Precision Engineering, 2008, 16(9): 1722-1726.
[8]任志英,高诚辉.小波变换在粗糙度表面几何形貌特征中的应用[J].中国工程机械学报,2013,11(1):78-82.
Ren Zhiying, Gao Chenghui. Applications of Wavelet Transform for Rough-surface Morphological Characterizations[J]. Chinese Journal of Construction Machinery, 2013,11(1):78-82.
[9]史荣昌,魏丰.矩阵分析[M].3版.北京:北京理工大学出版社,2010.
[10]赵学智,叶邦彦,陈统坚.多分辨奇异值分解理论及其在信号处理和故障诊断中的应用[J].机械工程学报, 2010, 46(20): 64-75.
Zhao Xuezhi, Ye Bangyan, Chen Tongjian. Theory of Multi-resolution Singular Value Decomposition and Its Application to Signal Processing and Fault Diagnosis[J]. Journal of Mechanical Engineering, 2010, 46(20): 64-75.
[11]曾文涵.双树复小波表面分析模型及加工过程形貌辨识方法研究[D].武汉:华中科技大学,2005.
[12]任志英,高诚辉,林建兴,等. 基于双树复小波变换的三维粗糙度表面评定方法研究[J].中国机械工程,2014, 25(13):1795-1799.
Ren Zhiying, Gao Chenghui, Lin Jianxing, et al. Evaluation Method of Three-dimensional Rough Surface Based on Dual-three Complex Wavelet Transform Methods[J]. China Mechanical Engineering, 2014, 25(13):1795-1799.
[13]任志英,高诚辉,申丁,等. 双树复小波稳健滤波在工程表面粗糙度评定中的应用[J]. 光学精密工程,2014, 22(7):1820-1827.
Ren Zhiying, Gao Chenghui, Shen Ding, et al. Application of DT-CWT Robust Filtering to Evaluation of Engineering Surface Roughness[J]. Optics and Precision Engineering, 2014, 22(7): 1820-1827.
(编辑王艳丽)
收稿日期:2015-07-20
基金项目:国家自然科学基金资助项目(51365009);桂林电子科技大学研究生教育创新计划资助项目(YJCXS201501)
中图分类号:TH161.14
DOI:10.3969/j.issn.1004-132X.2016.13.013
作者简介:吴芬,男,1990年生。桂林电子科技大学机电工程学院硕士研究生。主要研究方向为新一代GPS表面滤波技术。黄美发,男,1962年生。桂林电子科技大学机电工程学院教授、博士研究生导师。陈磊磊,男,1985年生。桂林电子科技大学机电工程学院助教。吴常林,男,1989年生。桂林电子科技大学机电工程学院硕士研究生。
A New Surface Filtering Technology Based on Multi-resolution Singular Value Decomposition
Wu FenHuang MeifaChen LeileiWu Changlin
Guilin University of Electronic Technology,Guilin,Guangxi,541004
Abstract:Recently, the way used to extract the surface evaluation reference existed some issues such as boundary effect,no multi-scale and the selection of wavelet basis function.Aimming at above problems,a theory called 1D multi-resolution singular value decomposition (MSVD) was introduced and a 2D MSVD was deduced.And a surface filtering method based on MSVD was provided according to the above theory.The filtering effectiveness has a good consistency with the existing surface filtering technology and this surface filtering is suitable to surface engineering evaluation.
Key words:surface morphology; multi-resolution; singular value decomposition(SVD); surface filtering

