基于偏导数的Sobol’总测度指标的上下限分析

宋述芳　周　桐　吕震宙

1.西北工业大学,西安,710072　　2.香港理工大学,香港,999077



基于偏导数的Sobol’总测度指标的上下限分析

宋述芳1周桐2吕震宙1

1.西北工业大学,西安,7100722.香港理工大学,香港,999077

摘要：以Sobol’主测度指标Si作为总测度指标i的下限，建立并推导了基于偏导数的测度指标作为i的新上限。基于泛函和Euler-Lagrange等式，进行了不同变量分布形式下(均匀、正态、指数、Beta、三角分布等)，Sobol’总测度指标i的基于偏导数的上限分析，并给出了新上限详细的推导过程和具体的计算公式。通过简单数值和工程算例，验证了新上限的精度及效率，为更准确地界定总测度指标i的取值区间提供了参考。

关键词：总测度指标；主测度指标；基于偏导数的测度指标；Euler-Lagrange等式

0引言

全局灵敏度(又称重要测度)指标可以全面反映模型输入变量的不确定性对模型输出响应不确定性的贡献程度，它在工程设计及概率安全评估中具有很重要的作用[1-6]。依据全局灵敏度指标的大小，为基本变量进行重要性排序，进而在设计和优化中优先或者重点考虑重要性程度高的基本变量或者忽略重要性程度低的基本变量，对系统工程设计和优化具有重要的指导作用。

1Sobol’的测度指标

文献[1-2,6]利用方差分析(analysis of variance, ANOVA)给出了基于方差的重要性测度指标。因而，一般的ANOVA分解被认为是基于方差的重要性分析的基础。ANOVA分解的前提是假设各子项期望为零且各子项正交，在这种假设下ANOVA的分解唯一，即功能函数Y=f(x)的唯一分解式为

(1)

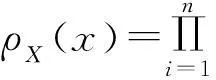
(2)

fij(xi,xj)表征两变量(xi,xj)的相互作用，它可以通过下式求得:

fi(xi)-fj(xj)-f0

(3)

类似地，可得到s(s=3,4,…,n)个变量的分解项fi1i2…is(xi1,xi2,…,xis)，也可称之为s阶交叉项，可通过对除这s个变量外的所有变量求数学期望后减去这s阶变量的任意子集影响及常数项f0得到。

考虑式(1)各分解项的正交特点，功能函数Y=f(x)的方差:

可以由各分解项方差之和表示，即

(4)

(5)

定义与变量xi有关的子项之和为ui(x)[14]，即

f1…n(x1,…,xn)=f(x)-∫Rf(x)ρXi(xi)dxi

(6)

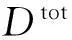
(7)

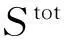
(8)

Di=var[E(Y|xi)]

(9)

(10)

其中，E(·)为期望算子，var(·)为方差算子，下标“-i”表示除xi以外的变量，即x-i=(x1,…,xi-1,xi+1,…,xn)，从而可得到输入变量xi的重要性测度两个指标的计算表达式分别为

(11)

(12)

求解Sobol’测度指标的方法有很多，如基于MC或QMC模拟的方法(如式(11)、式(12))，随机抽样的高维模型替代法(HDMR)等(如式(5))，这些方法多涉及双重抽样分析，计算量较大。我们更期望找到较简单的计算方式以获得总测度指标的区间，进而确定变量的重要性排序。

2文献中的Sobol’总测度指标的上下限

2.1下限(lowerbound,LB)

2.2上限(upper bound, UB)

Sobol’等[12]提出的基于偏导数的测度指标(DGSM)定义为对模型输出偏导数平方的积分。假设模型函数Y=f(x)，其输入变量x=(x1,x2,…,xn)是相互独立的随机向量，其联合概率密度函数和累积分布函数分别为ρX(x)和FX(x)，如果∂f/∂xi存在并且平方可积，变量xi的DGSM指标υi为

(13)

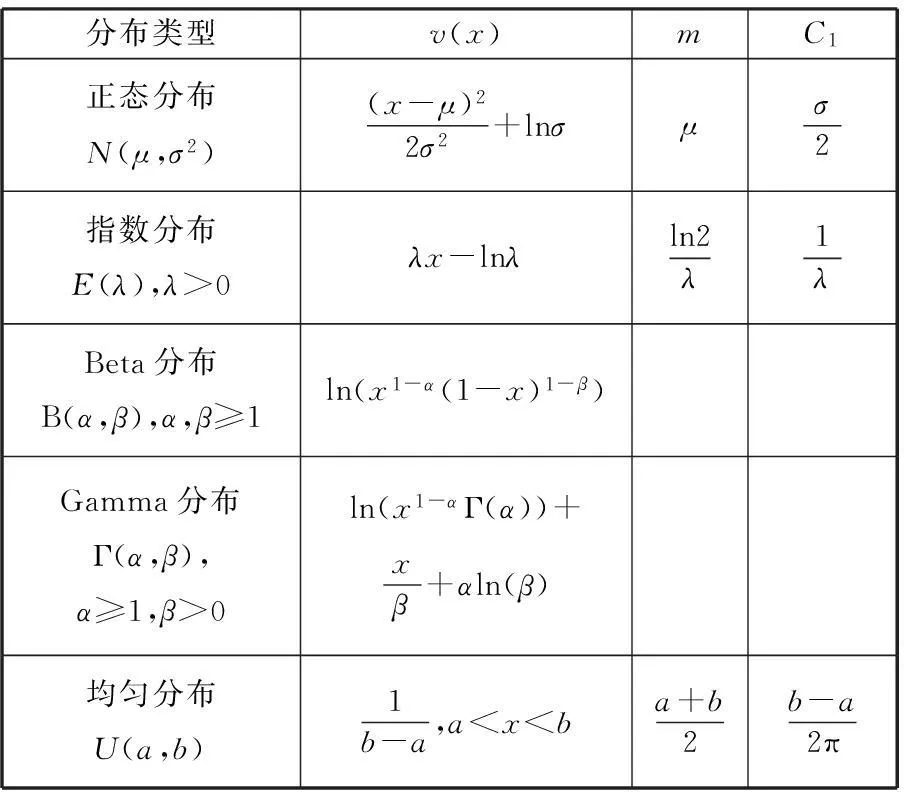
表1　满足log-concave概率分布情况下的

定理1在以下假设条件下：①随机输入变量相互独立；②函数f(x)为实函数；③f(x)的一阶导数为实函数；④随机变量xi的分布是Boltzman概率测度，有

(14)

其中，FXi(xi)为随机变量xi的累积分布函数。

定理2在以下假设条件下：①随机输入变量相互独立；②函数f(x)为实函数；③f(x)的一阶导数为实函数；④随机变量xi的分布是log-concave概率测度, 有

(15)

3.1均匀分布

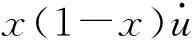
(16)

并且当且仅当u是常数的时候等号成立。

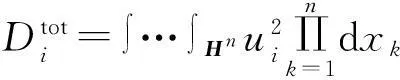
(17)

其中，Hn为n维的超立方体空间，ui为与变量xi有关的项。

根据变量代换可得出(a,b)区间上的均匀分布变量的总测度指标的新上限为

(18)

3.2其他变量分布类型

假设对于其他分布，构造如下形式的上限：

(19)

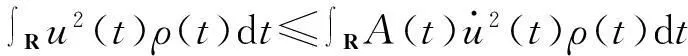
假设Φ=Φ[u]是一个关于u(t)的泛函，即

(20)

将积分不等式转化为变分法求泛函极值的问题，当u(t)满足∫Ru(t)ρ(t)dt=0时使得泛函Φ[u]最小。假设泛函有极值函数u*=t-μ，其中μ是随机变量t的平均值，此极值函数需满足Euler-Lagrange方程：

(21)

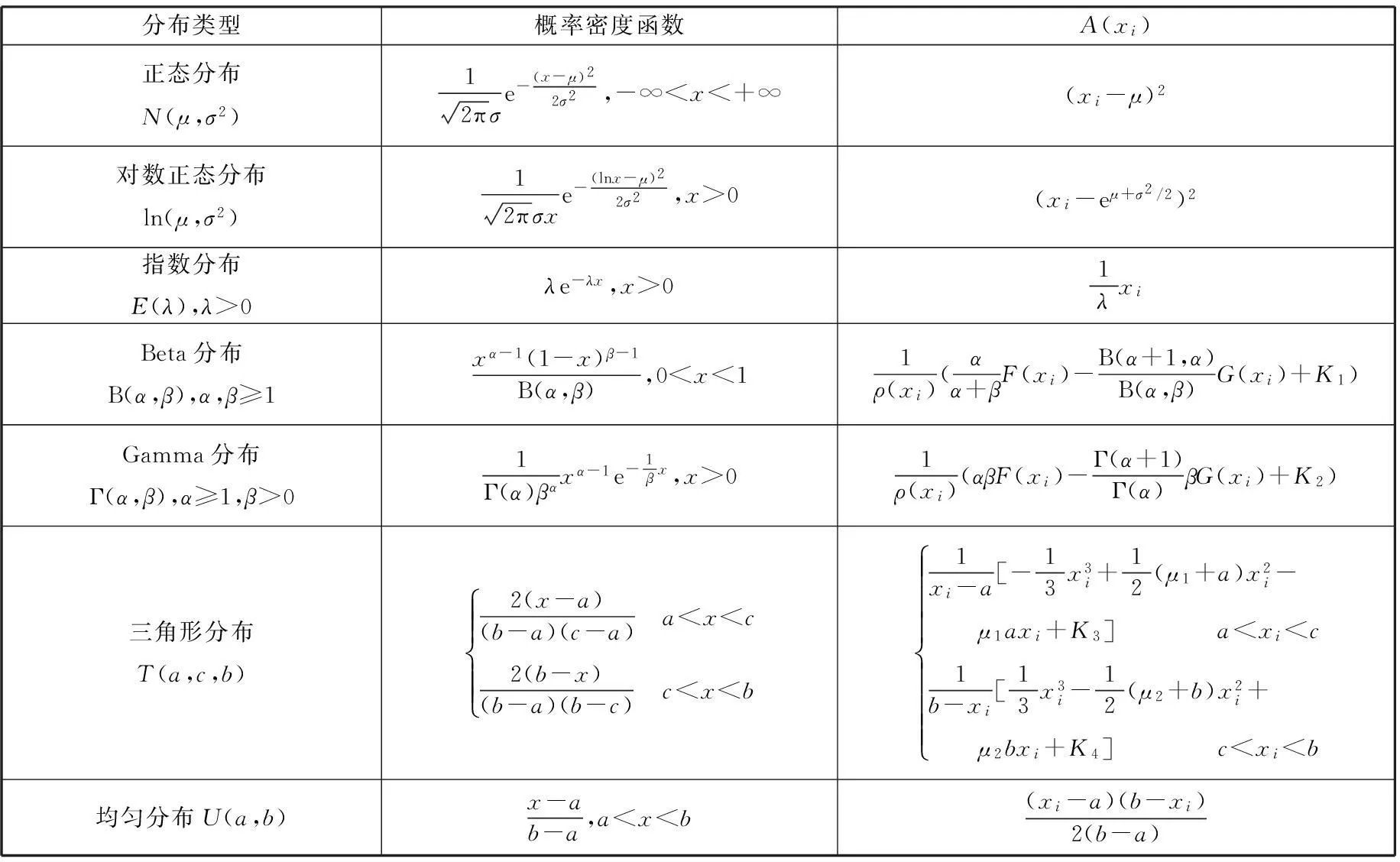
表2　满足log-concave概率分布情况下的新上限A(xi)函数

表2中的常数K1、K2、K3和K4分别为

K2≥0

4算例及分析

将文献[12-13]提出的基于偏导数的测度指标DGSM称为γUB1，本文所提出的新上限称为γUB2，通过对不同分布、不同类型的功能函数进行测试，验证其正确性与有效性。

4.1数值算例

4.1.1均匀分布算例

算例1～3的函数及测度指标结果显示列于表3，其中所有输入变量均服从(0,1)区间上的均匀分布，变量之间相互独立。

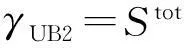
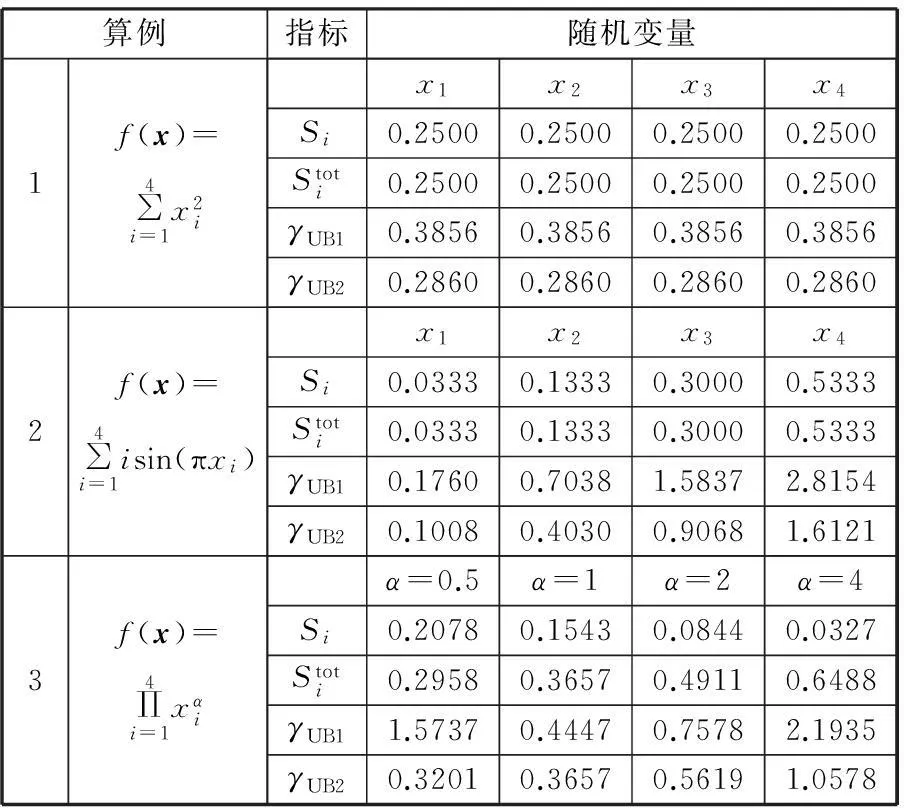
表3　算例1～3的函数及测度指标结果对比

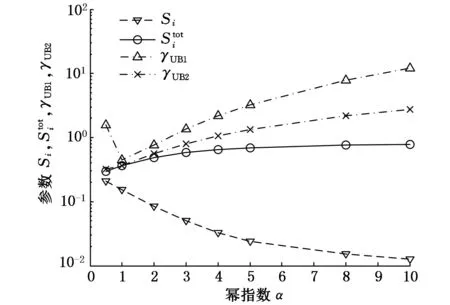
图1　算例3的随α的变化趋势图

4.1.2指数分布算例

算例4～6的函数及测度指标结果参见表4，其中输入变量x1,x2,x3,x4分别服从均值为1,2,3,4的指数分布，变量之间相互独立。

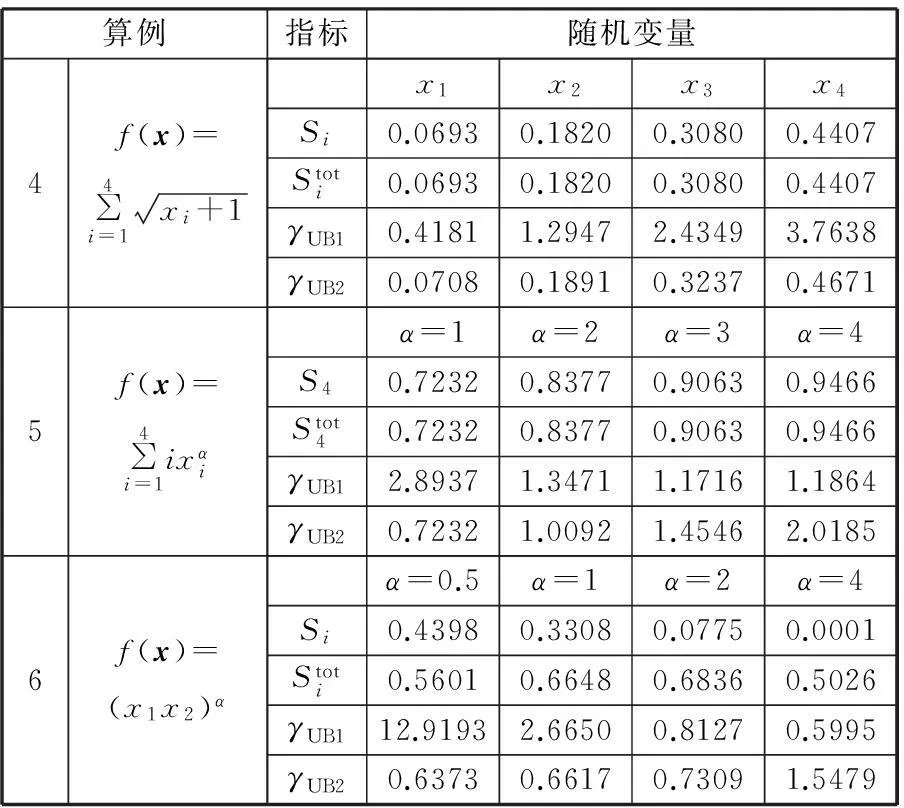
表4　算例4～6的函数及测度指标结果对比

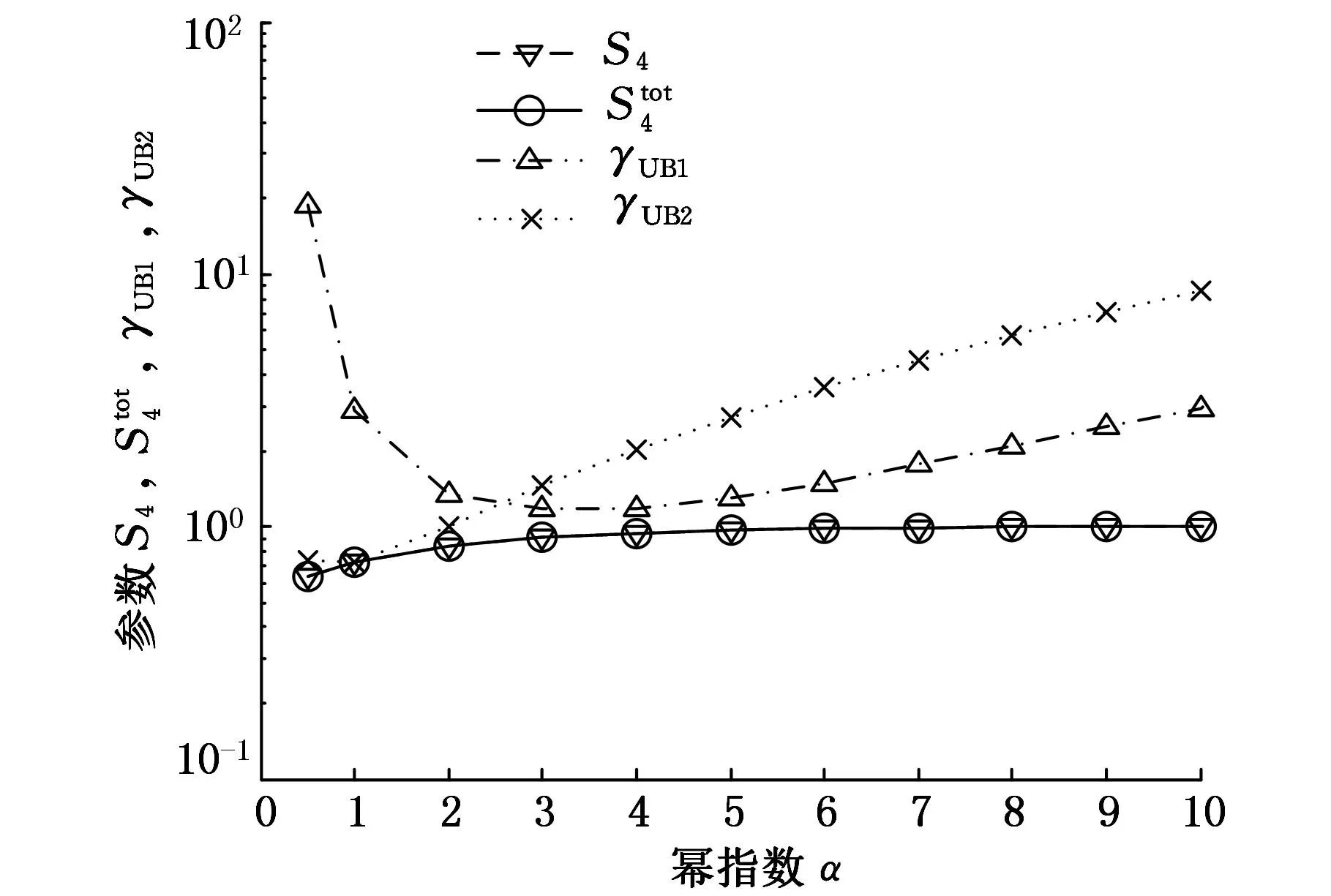
图2　算例5的随α的变化趋势图

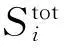
工程算例1悬臂梁结构在自由端受到载荷P作用，以自由端位移不超过0.004 m建立极限状态方程为

其中，弹性模量E=200 GPa。将梁的长L、宽b和高h看作随机变量，其均值分别为0.5 m，0.02 m，0.05 m，标准差为0.05 m，0.002 m，0.005 m，其中，L和h为对数正态分布变量，b为正态分布变量，载荷P为(200，400)N的均匀分布变量。该算例的测度指标对比表参见表5。

表5　工程算例1的测度指标结果对比

从表5可以看出，两种上限给出的变量重要性排序是一致的，且都能够很好地找出对输出响应影响小的两个参数b和h，均匀分布时指标γUB2比γUB1好，正态分布时指标γUB1≤γUB2，当且仅当为正态线性函数时，等号成立。

工程算例2基于材料的蠕变和疲劳试验数据，并考虑一级载荷水平，文献[17]采用如下非线性极限状态方程来定义失效与安全的边界线：

g(Nc,Nf,nc,nf,θ1,θ2)=

Dc=nc/NcDf=nf/Nf

其中，θ1和θ2为从试验数据中得到的两个参数；Nc与Nf分别为蠕变寿命和疲劳寿命；nc和nf分别为蠕变载荷和疲劳载荷作用的实际周次。

文献[17]依据试验分析，假定上述极限状态方程中的基本随机变量Nc、Nf、nc、nf均服从对数正态分布，θ1和θ2服从正态分布(表6)，则该算例的测度指标对比参见表7。

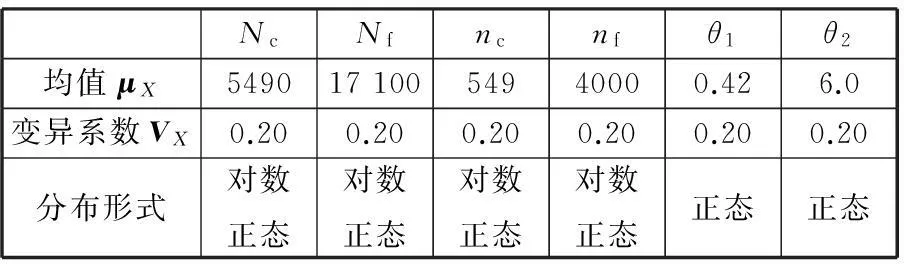
表6　基本变量分布形式

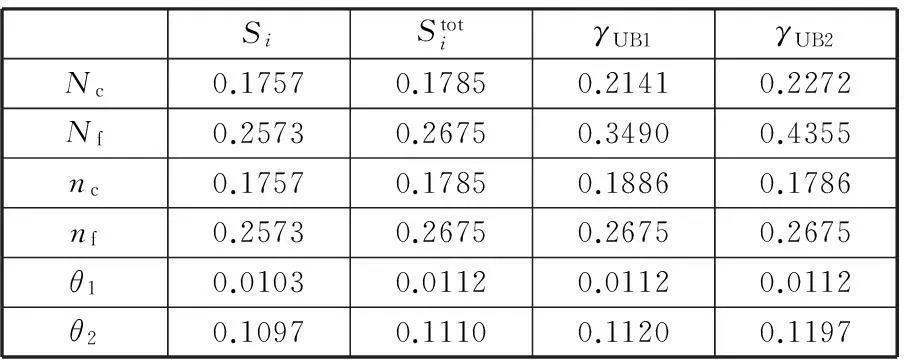
表7　工程算例2的测度指标结果对比

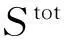
工程算例3单层单跨结构(图3)的极限状态方程为

f(x)=0.01 m-u3(A1,A2,P)=

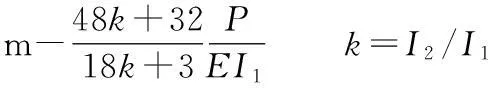
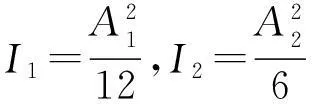
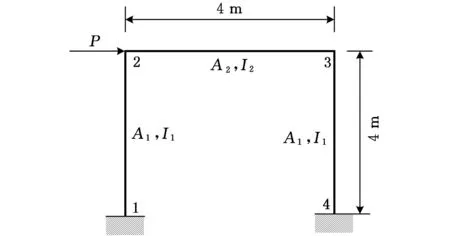
图3　单层单跨结构

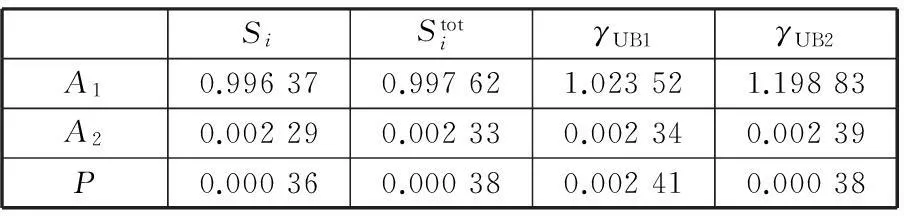
SiStotiγUB1γUB2A10.996370.997621.023521.19883A20.002290.002330.002340.00239P0.000360.000380.002410.00038

5结语

本文围绕Sobol’总测度指标和基于偏导数的测度指标进行了如下工作：建立了(0,1)区间上均匀分布变量的偏导数测度指标，并将其作为Sobol’总测度指标的新上限，在此基础上基于泛函和Euler-Lagrange等式，推导出了正态分布、指数分布、Beta分布、三角分布等分布形式的偏导数测度指标公式。采用QMC方法，在输入变量服从不同分布，不同的功能函数情况下，计算出不同测度指标，并比较它们之间的关系，从理论和数值上证实了所提指标的可靠性。通过算例比较分析得出，对于均匀分布来说，大多数情况下，γUB2优于γUB1，对于指数分布来说，当函数非线性程度不高时，γUB2的优越性还是很明显的，但随着函数非线性程度的提高，γUB1的优势逐渐显现出来。此外，γUB2和γUB1确定的变量重要性排序和总测度指标基本一致。

参考文献：

[1]吕震宙,李璐祎,宋述芳,等. 不确定性结构系统的重要性分析理论与求解方法[M].北京:科学出版社，2015.

[2]Sobol’IM.GlobalSensitivityIndicesforNonlinearMathematicalModelsandTheirMonteCarloEstimates[J].MathematicsandComputerinSimulation, 2001, 55(1):221-280.

[3]BorgonovoE.MeasuringUncertaintyImportance:InvestigationandComparisonofAlternativeApproaches[J].RiskAnalysis, 2006, 26(5): 1349-1361.

[4]BorgonovoE.ANewUncertaintyImportanceMeasure[J].ReliabilityEngineering&SystemSafety, 2007, 92(6):771-784.

[5]SaltelliA.SensitivityAnalysisforImportanceAssessment[J].RiskAnalysis, 2002, 22(3): 579-590.

[6]SaltelliA,AndresM,CampolongoF,etal.GlobalSensitivityAnalysis:thePrimer[M].NewYork:JohnWiley&SonsLtd., 2008.

[7]FeilB,KucherenkoS,ShahN.ComparisonofMonteCarloandQuasiMonteCarloSamplingMethodsinHighDimensionalModelRepresentation[C]//TheFirstInternationalConferenceonAdvancesinSystemSimulation.Porto,SIMUL, 2009:12-17.

[8]Sobol’IM,KucherenkoS.OnGlobalSensitivityAnalysisofQuasi-MonteCarloAlgorithms[J].MonteCarloMethodsandSimulation, 2005, 11(1): 1-9.

[9]LiGY,HuJS,WangSW,etal.RandomSampling-highDimensionalModelRepresentation(RS-HDMR)andOrthogonallyofItsDifferentOrderComponentFunctions[J].JournalofPhysicalChemistryA, 2006, 110(7): 2474-2485.

[10]FeilB,KucherenkoS,ShahN.VolatilityCalibrationUsingSplineandHighDimensionalModelRepresentationModels[J].Wilmott, 2009, 1(2): 179-195.

[11]KucherenkoS,SongS,ComparisonofDifferentNumericalEstimatorsforMainEffectGlobalSensitivityIndices[C]//1stECCOMASThematicConferenceonUncertaintyQuantificationinComputationalSciencesandEngineering.CreteIsland, 2015:22-53.

[12]Sobol’IM,KucherenkoS.DerivativebasedGlobalSensitivityMeasuresandTheirLinkwithGlobalSensitivityIndices[J].MathematicsandComputersinSimulation, 2009, 79(10): 3009-3017.[13]IoossB,PopelinAL,BlatmanG,etal.SomeNewInsightsinDerivative-basedGlobalSensitivityMeasures[C]//ProceedingsofPSAM11 &ESREL2012Conference.Helsinki, 2012: 1094-1104.

[14]KucherenkoS,SongS.Derivative-basedGlobalSensitivityMeasuresandTheirLinkwithSobol’SensitivityIndices[C]//MonteCarloandQuasi-MonteCarloMethods.KULeuven:SpringerInternationalPublishingSwitzerland, 2014: 23-38.

[15]BobkovSG.IsoperimetricandAnalyticInequalitiesforLog-concaveProbabilityMeasures[J].TheAnnalsofProbability, 1999, 27(4): 1903-1921.

[16]HardyGH,LittlewoodJE,PolyaG.Inequalities[M]. 2nded.Cambridge:CambridgeUniversityPress, 1973.

[17]MaoHY,MahadevanS.ReliabilityAnalysisofCreep-fatigueFailure[J].InternationalJournalofFatigue, 2000, 22(9): 789-797.

(编辑王艳丽)

收稿日期：2015-08-03

基金项目：国家自然科学基金资助项目(NSFC51308459)；中央高校基本科研业务费专项资金资助项目(310201401JCQ01014，3102015BJ(Ⅱ)CG009)

中图分类号：TP302.7

DOI：10.3969/j.issn.1004-132X.2016.13.014

作者简介：宋述芳,女,1982年生。西北工业大学航空学院副教授。主要研究方向为飞行器设计、飞行器可靠性工程。发表论文30余篇。周桐，男,1993年生。香港理工大学机械工程学院博士研究生。吕震宙,女,1966年生。西北工业大学航空学院教授、博士研究生导师。

Analyses for Lower and Upper Bounds of Sobol’ Total Sensitivity Index Based on Derivative

Song Shufang1Zhou Tong2Lü Zhenzhou1

1.Northwestern Polytechnical University，Xi’an,710072 2.Hongkong Polytechnical University,Hongkong,999077

Abstract:A main sensitivity index Si was set as the lower bound of i and the new upper bound of i was built based on the derivative. On the basis of functional analysis and Euler-Lagrange equation, the new upper bound of i based derivative was analyzed for different variable distribution types, such as uniform, normal, exponential, triangular, Beta distribution etc. The derived process and formulas were presented in detail. Several numerical and engineering examples were used to verify the precision and efficiency of the presented bounds, which may provide the accurate bounds of i.

Key words：total global sensitivity index;main global sensitivity index;derivative based global sensitivity index;Euler-Lagrange equation