结构弹性对桨距角突变下风力机气动性能的影响

刘　翀，　刘鹏寅,　沈　昕,　竺晓程

(上海交通大学 机械与动力工程学院，上海 200240)



结构弹性对桨距角突变下风力机气动性能的影响

刘翀，刘鹏寅,沈昕,竺晓程

(上海交通大学 机械与动力工程学院，上海 200240)

摘要：对桨距角突变情况下的风力机气动性能进行了数值模拟，着重分析了风力机叶片非对称性、叶片结构弹性及塔架结构弹性对气动性能的影响，并模拟了桨距角突变情况下风力机气动性能的过冲现象.结果表明：变桨前后主轴扭矩的波动主要是由于风力机2个叶片质量非对称引起的，而风力机叶片结构弹性加剧了风轮主轴扭矩在过冲过程的振荡；风力机叶片非对称性、叶片结构弹性及塔架结构弹性共同作用是导致轴向推力出现波动的主要原因.

关键词：风力机； 气动性能； 桨距角； 叶片结构弹性； 塔架结构弹性； 数值模拟

近年来，随着风力机单机容量的不断增加，风力机效率、安全性能及输电品质对电网的影响越来越大.风力机在运行过程中将遇到运行工况瞬间改变的情况(如桨距角突变)，此时风轮上的载荷无法同步变化，导致气动参数迅速改变至峰值，并经过一段时间才能达到新的稳定状态，该过程又称为过冲现象.过冲现象通过对气动阻尼的影响使风力机各部件振动，对风力机稳定性以及部件寿命带来不利影响[1-2].而目前常采用的双馈异步风力机对电网电压暂降较为敏感，这需要风力机及时有效地通过变桨距等方法来控制气动性能，并输出无功功率支撑电压[3-5].因此，在对风力机进行研究分析时，需要分析桨距角突变时的气动性能.

沈昕等[6-7]采用时间步进自由尾迹法对变桨情况下风力机气动性能进行了模拟分析，在验证模拟方法的同时，发现过冲现象是由桨距角变化导致诱导速度发生改变而引起的，并提出了实测值存在的振荡现象可能是由风力机塔架所受推力变化导致其自身振动引起的；Niebsch等[8]提出风轮叶片的非对称性将引起风力机载荷变化，并通过风力机整机振动影响其气动性能；刘雄等[9]在对风力机叶片动态响应分析中发现，叶片在工作过程中易受较大振动和变形，从而影响到叶片自身的气动性能；李德源等[10]在对大型风力机塔架涡致振动的研究分析中得出，由于非定常力的作用塔架上将引起结构振动，进而影响整机气动性能.Chattot等[11]在利用升力线法模拟风力机气动性能情况时，针对实验测量中出现的主轴扭矩和轴向推力的振荡问题，认为这是由于塔架结构的弹性振动导致的.

上述研究分析中，虽然都提到叶片和塔架会通过结构振动在桨距角突变情况下对风力机气动性能产生影响，但并未对其进行深入的模拟分析.因此，笔者以两叶片水平轴小型风力机作为研究对象，探讨桨矩角突变情况下主轴扭矩和轴向推力波动性加剧的问题，分析了叶片结构弹性及塔架结构弹性对风力机气动性能的影响，最终发现了叶片非对称性对风力机气动性能的重要影响.

1数值模拟方法

数值模拟软件采用由美国可再生能源实验室(NREL)研发的FAST开源软件.该软件专门应用于两叶片及三叶片水平轴风力机的气动弹性模拟.FAST开源软件的气动参数求解主要基于叶素理论(BEM)及广义动态尾迹理论(GDW)，而结构动态特性求解主要基于KANE方程，其将风力机作为一个刚柔部件组合的动力系统来建立动力学方程进而求解[12-13].

叶素理论是目前使用最广泛的风力机叶片气动性能分析理论，该理论主要基于叶素理论和动量理论.根据叶素理论，在半径为r位置的环形区域中叶素产生的推力T和转矩Q分别为

(1)

(2)

式中：ρ为来流密度；U为来流速度；CL、CD分别为叶素翼型的升力系数和阻力系数；φ为入流角；B为叶片数；c为该叶素弦长.

根据动量定理，该环形区域中叶素所产生的推力和转矩可表示为

(3)

(4)

式中：a、a′分别为轴向速度诱导因子和切向速度诱导因子；Ω为风轮角速度.

在此基础上考虑叶尖、轮毂损失影响，并增加葛劳渥特湍流尾迹修正模型，再通过迭代方法计算出沿叶展方向上每个叶素的诱导速度、攻角以及推力系数，再进一步求解叶片上各气动性能参数.

广义动态尾迹理论基于加速度势方法，并考虑了诱导速度的时间滞后效应，是解决风力机非定常尾迹动力学问题的有效方法.该理论基于拉普拉斯方程势流解，并在转子径向、方位角方向分别采用无穷级数的勒让德函数和三角函数加以描述，并在具体算法中限定压力分布、诱导速度场的有限计算级数进行求解[14].

以NREL Phase VI风力机作为研究对象.NREL对该风力机进行了风洞实验，并提供了其在稳定和非稳定工况下的实验数据.风力机使用双叶片转子，叶片半径为5.03 m，质量为60.4 kg.叶片弦长沿半径线形变化，扭角沿半径非线性变化，叶片在整个展向均使用NREL S809翼型.风轮转速为72 r/min(即风轮旋转频率为1.2 Hz)，风向为上风且正对风轮[15].

分阶段来看，2005—2011年，＜，尽管海南省旅游经济发展滞后于生态环境的保护和建设力度，但是增长速度较快，且蕴含着极大的发展潜力；2012—2015年，＞，海南省生态环境的保护和建设滞后于旅游经济的发展，表明自2010年国际旅游岛建设上升为国家战略以后，旅游经济继续保持稳定大幅度增长，但是随着旅游业规模的不断扩大和发展，生态环境质量也在不断下滑，不过从2015年开始出现的小幅上升表明了海南省对于生态环境保护意识的觉醒。

2模拟结果与分析

2.1研究方法准确性验证

为了验证研究方法的准确性，首先模拟风力机在不同风速下的气动性能，并与NREL对其在相同条件下的实测结果进行对比.图1给出了不同风速下的风轮轴向推力和主轴功率.从图1可以看出，模拟结果与实测结果基本吻合.随着风速的增大，轴向推力逐步增大；在低风速下(小于9 m/s)主轴功率随着风速的增大而升高；当风速超过9 m/s后，随着风速的增大主轴功率基本保持不变，这是由于随着风速的增大，叶片与空气的相对速度增大，攻角增大，叶片进入失速运行状态.对比结果初步验证了所采用数值模拟方法的准确性.

对风力机在5 m/s稳定风速下，桨距角以66.0°/s角速度从-6°突变到10°时风力机的轴向推力和主轴扭矩进行数值模拟.图2给出了在叶片对称、叶片及塔架结构为刚性条件下的模拟结果与实测结果对比图.从图2可以看出，模拟结果与实测结果的趋势基本相符，成功模拟了桨矩角突变情况下的过冲现象；但模拟结果中过冲前后的气动性能曲线未出现实测结果相同的波动现象，且主轴扭矩的过冲情况与实测结果差别较大.

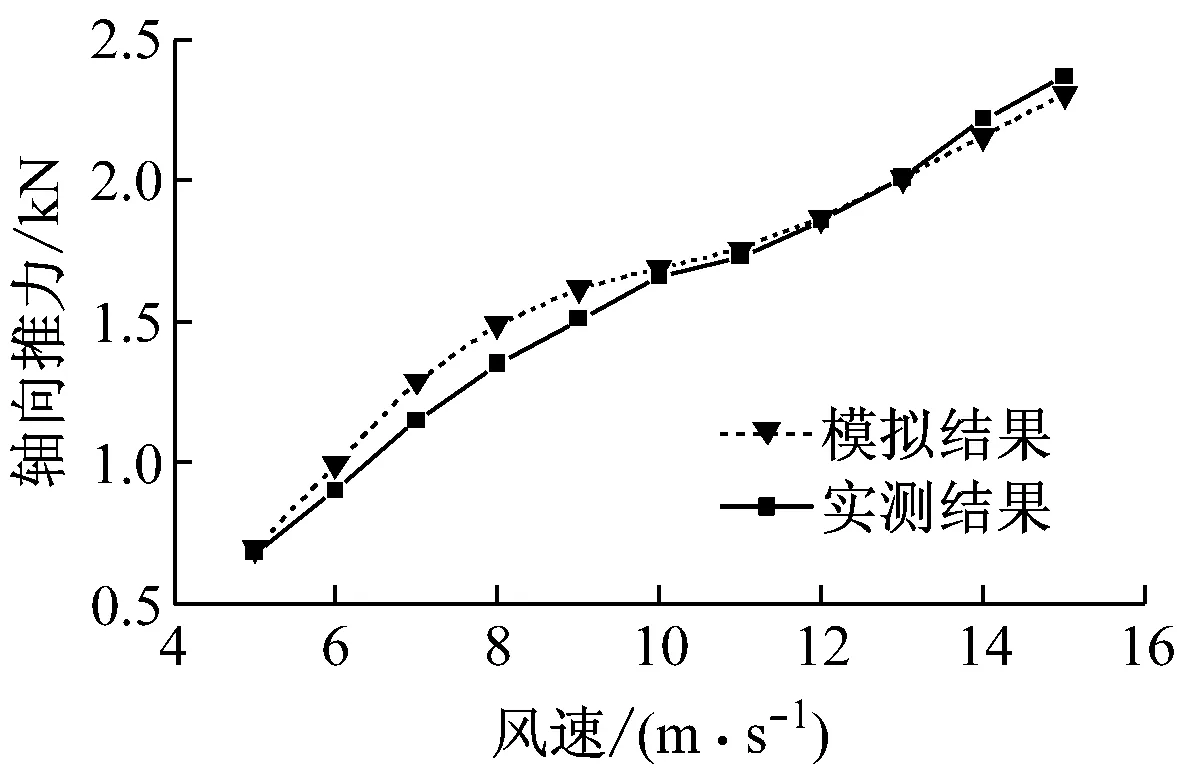
(a) 轴向推力

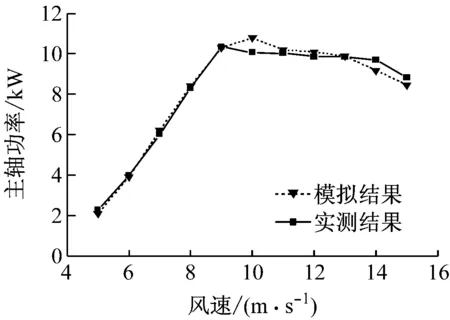
(b) 主轴功率

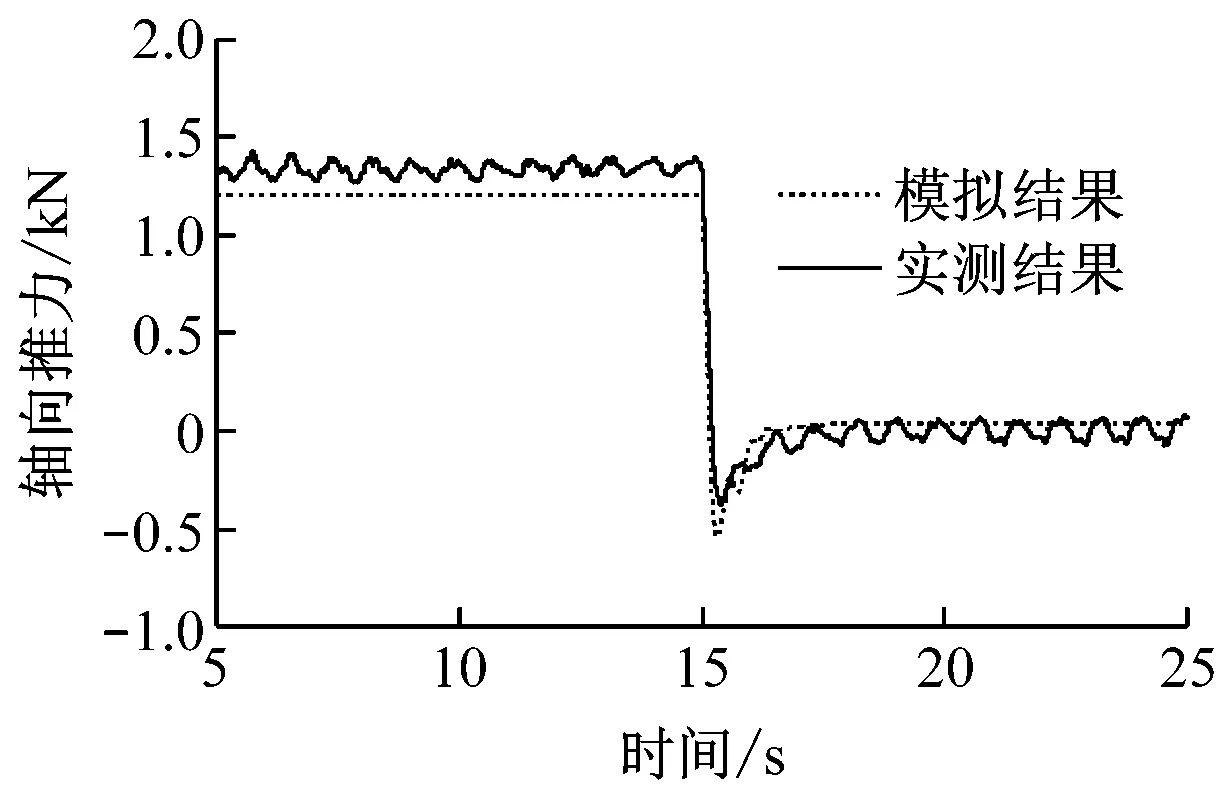
(a) 轴向推力

(b) 主轴扭矩

Fig.2Comparison of aerodynamic performance between experiment and simulation with rigid blades and tower

2.2叶片非对称性对气动性能的影响

分析图2中过冲前后的实测结果，发现其轴向推力和主轴扭矩均出现频率为1.2 Hz的波动，这与风轮转频相等.实验所采用的风轮为双叶片结构，每个叶片质量均为60.4 kg，其中一个叶片上安装有0.45 kg的测量探针，该质量仅占叶片总质量的0.37%.因此，之前对该模型的研究分析中此微小质量非对称性均被忽略.上述气动性能的波动现象可能是由该质量非对称性导致风轮旋转不平衡引起的，故在设定模拟参数时，在其中一个叶片上添加质量为0.45 kg的质量块.

图3为考虑叶片非对称性时的模拟结果与实测结果的对比图.对比图2(a)和图3(a)可知，风轮轴向推力基本没有变化，说明叶片非对称性对轴向推力没有直接影响；对比图2(b)和图3(b)可知，主轴扭矩在过冲前后出现较明显的波动，该波动频率同为1.2 Hz，波动幅值略小于实测结果，说明风轮叶片微小的非对称性是引起风轮主轴扭矩出现较大幅度波动的主要原因.

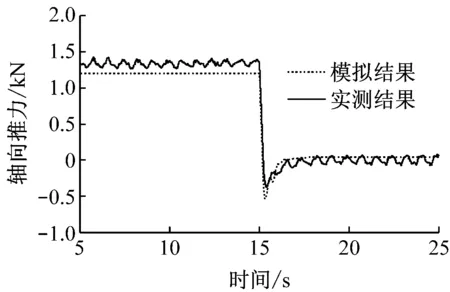
(a)轴向推力

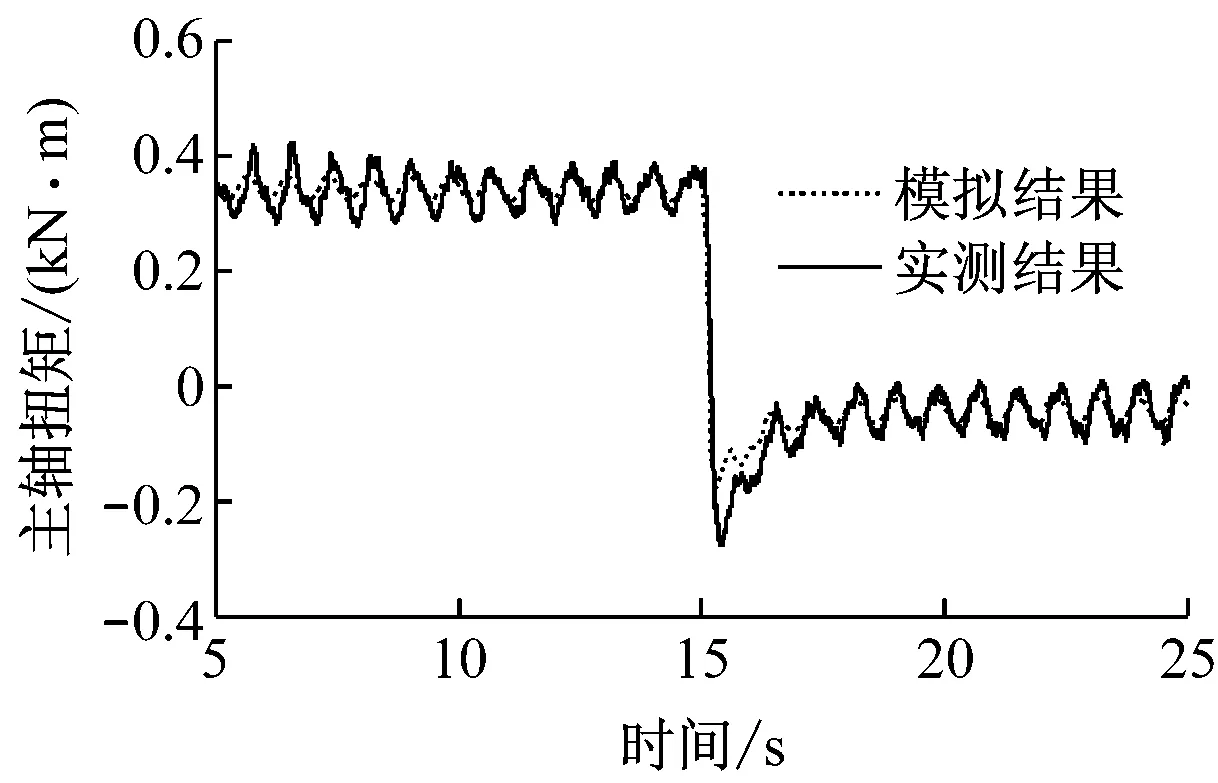
(b)主轴扭矩

Fig.3Comparison of aerodynamic performance between experiment and simulation with imbalanced rotor

2.3叶片结构弹性对气动性能的影响

在考虑叶片非对称性的基础上进一步研究叶片结构弹性对风力机轴向推力和主轴扭矩的影响，模拟结果与实测结果见图4.

对比图3(a)与图4(a)可知，是否考虑叶片结构弹性对风力机所受轴向推力没有影响；对比图3(b)与图4(b)可知，在考虑叶片结构弹性后，主轴扭矩在过冲过程中出现振荡加剧的现象.这是由于当叶片桨距角突变时，其攻角也随之发生改变，致使叶片上的气流诱导速度随之改变，进而引起叶片上气动力分布变化，叶片产生振动，从而影响叶片上的气流运动，形成复杂的流固耦合，导致在变桨引起的过冲过程中主轴扭矩波动加剧.

2.4塔架结构弹性对气动性能的影响

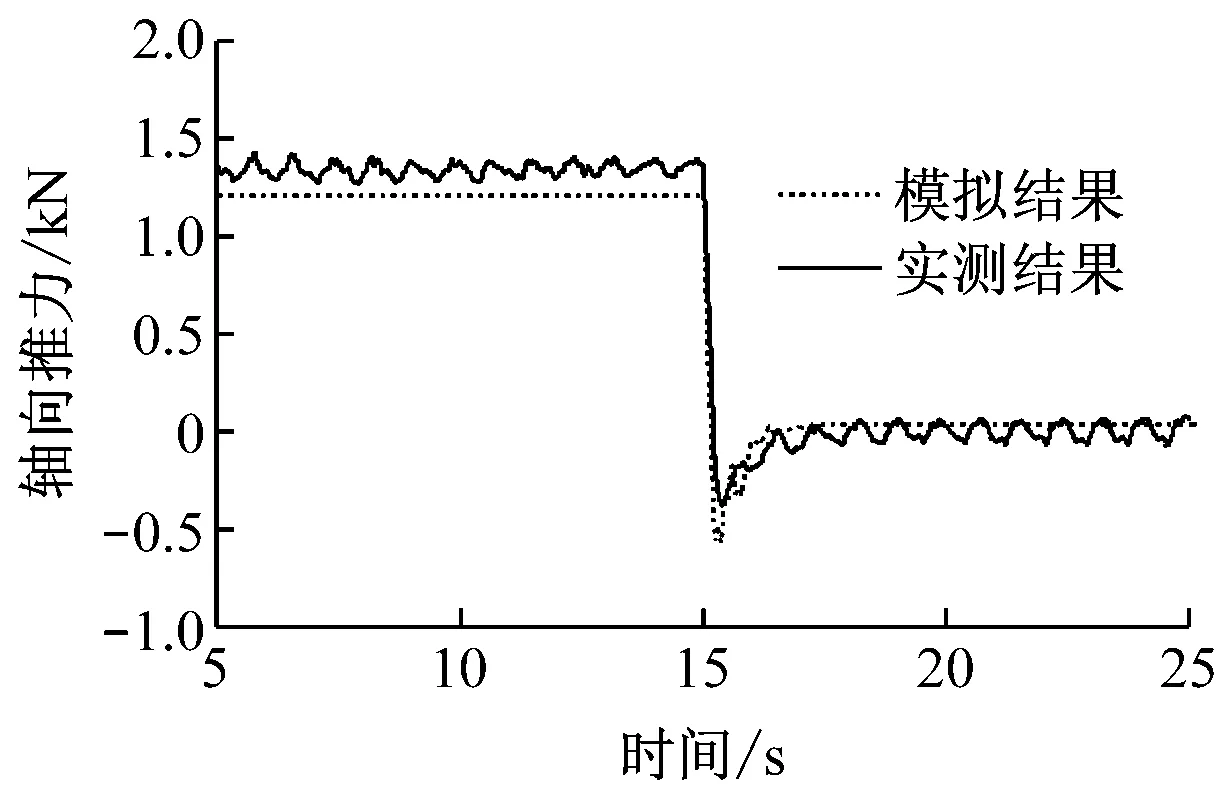
(a)轴向推力

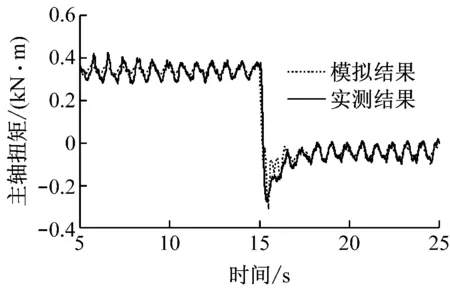
(b)主轴扭矩

Fig.4Comparison of aerodynamic performance between experiment and simulation with flexible blades

从图5(a)可以看出，考虑塔架结构弹性后，轴向推力在过冲过程中出现振荡加剧的情况，这是由于当桨距角突变时，作用在风力机上的气动力发生改变，当塔架结构为弹性体时将产生塔架前后振动，进而影响过冲过程的轴向推力大小；过冲后，塔架振动在结构阻尼的作用下逐渐衰减，导致轴向推力也逐渐减小并趋于平缓；但在过冲前稳定状态下，轴向推力并未出现与实测结果相同的波动；对比图3(b)与图5(b)可知，是否考虑塔架结构弹性对主轴扭矩的影响不大，再次证明叶片结构弹性是主轴扭矩出现过冲振荡加剧的主要影响因素.

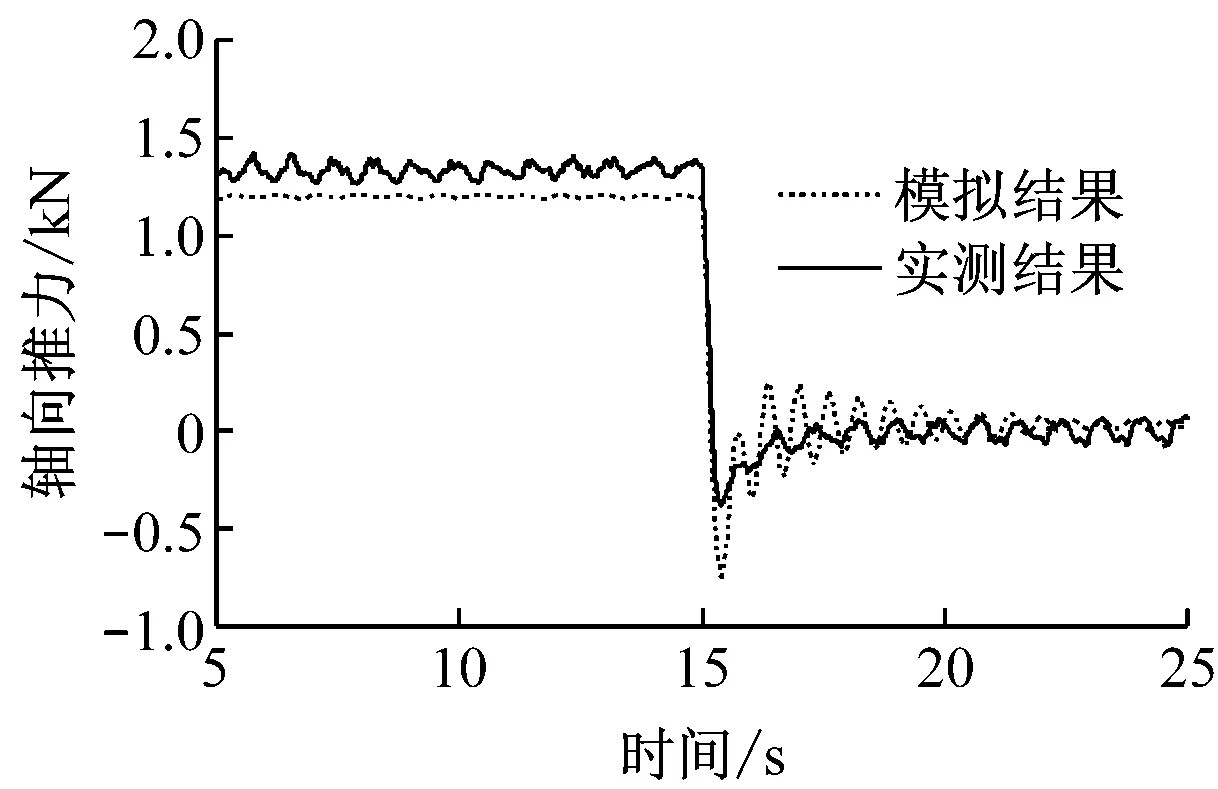
(a)轴向推力

(b)主轴扭矩

Fig.5Comparison of aerodynamic performance between experiment and simulation with flexible tower

2.5叶片结构弹性和塔架结构弹性对气动性能的影响

综合考虑叶片非对称性、叶片结构弹性及塔架结构弹性对风力机气动性能的影响，模拟结果与实测结果对比如图6所示.

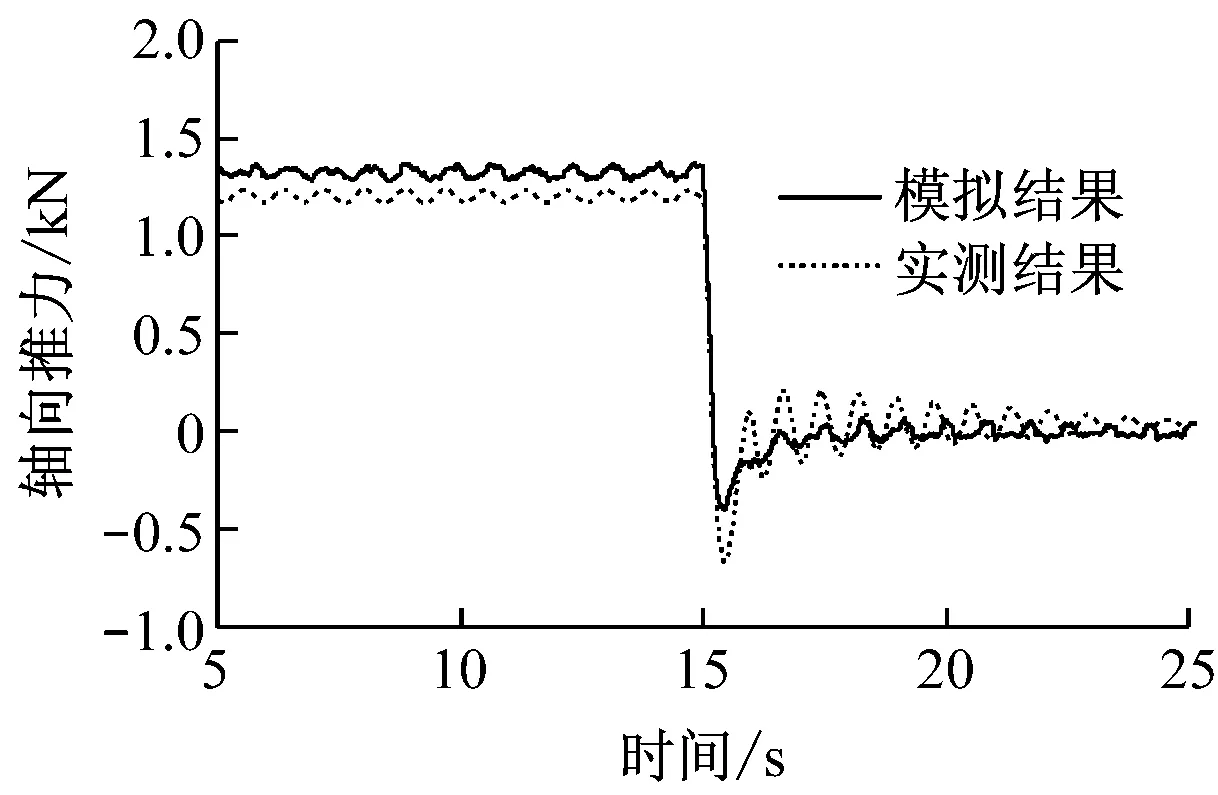
(a)轴向推力

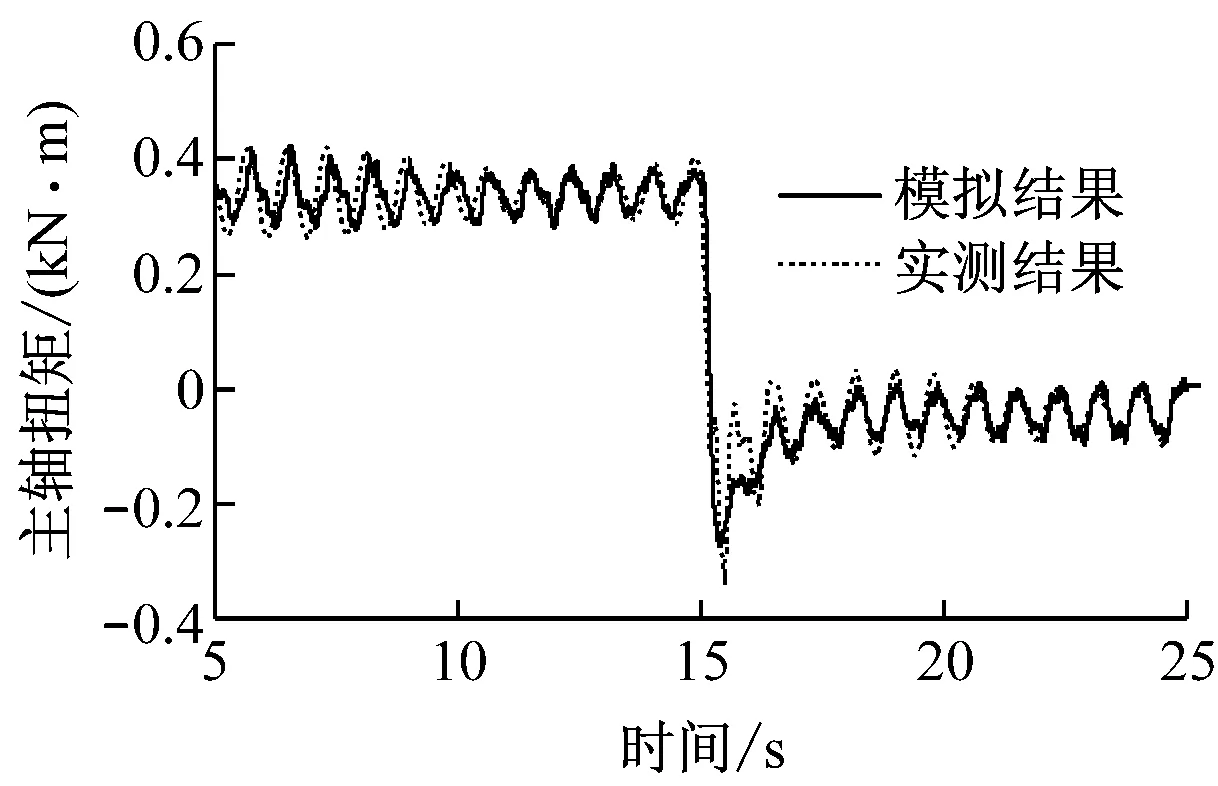
(b)主轴扭矩

Fig.6Comparison of aerodynamic performance between experiment and simulation with flexible blades and tower (imbalanced rotor)

对比图5(a)与图6(a)可知，考虑叶片结构弹性及塔架结构弹性后，在过冲前后模拟所得轴向推力出现与实测结果相近的波动，桨距角突变带来的塔架瞬态振动在结构阻尼作用下逐步衰减，最终仅剩旋转不平衡所产生的塔架振动，轴向推力仅在该振动条件下才能得出与实测结果相近的波动性能.对比图5(b)与图6(b)可知，模拟所得主轴扭矩波动情况也有所加剧.这是由于风力机叶片上的气动力通过叶片结构传递给其他风力机部件[16]，而且综合考虑塔架及叶片结构弹性后，整体系统的固有频率为1.7 Hz，该频率与叶轮旋转频率1.2 Hz相近，导致风轮主轴扭矩曲线波动幅值增加.

为了进一步验证叶片非对称性对轴向推力的影响，忽略叶片非对称性影响，考虑叶片结构弹性及塔架结构弹性时的模拟结果与实测结果对比见图7.与图6(a)相比，图7(a)中模拟结果在过冲前未出现波动现象；图7(b)中，主轴扭矩模拟结果与实测结果相差较大.结合图3可知，叶片非对称性对风轮所受轴向推力有间接影响.

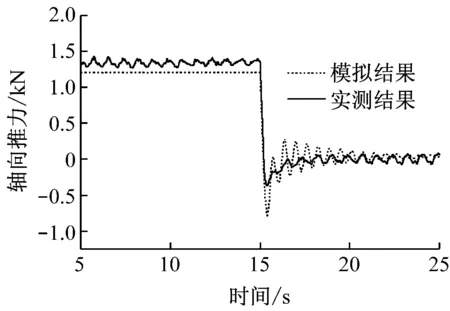
(a)轴向推力

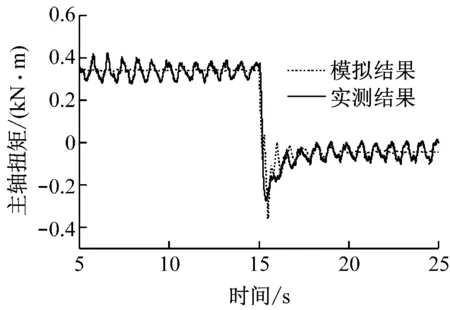
(b)主轴扭矩

Fig.7Comparison of aerodynamic performance between experiment and simulation with flexible blades and tower (balanced rotor)

3结论

(1)叶片上微小质量的非对称会影响风力机气动性能波动，在研究过程中不能忽略.该非对称性是过冲前后主轴扭矩产生波动的直接原因，对风轮所受轴向推力有间接影响.

(2)考虑叶片结构弹性后，风轮主轴扭矩在过冲过程中出现振荡加剧现象；考虑塔架结构弹性后，风轮轴向推力在过冲过程中出现振荡加剧现象.

(3)综合叶片非对称性、叶片结构弹性及塔架结构弹性后，在过冲前后风轮的轴向推力才出现类似于实测结果得到的波动，由此说明风力机整体的流固耦合是导致轴向推力出现波动的主要原因.

参考文献：

[1]SNEL H, SCHEPERS J G. Investigation and modelling of dynamic inflow effects[M].Netherlands: Netherlands Energy Research Foundation ECN, 1993.

[2]沈昕,俞国华,竺晓程,等.瞬变工况风力机气动性能预测[J].上海交通大学学报,2013, 47(3):392-397.

SHEN Xin,YU Guohua,ZHU Xiaocheng,etal. Aerodynamic investigation of wind turbine during pitching motion[J].Journal of Shanghai Jiaotong University,2013,47(3):392-397.

[3]叶航冶.风力发电机组检测与控制[M].上海:机械工业出版社, 2011.

[4]仇永兴，梁俊宇，康顺.电网电压跌落过程中风轮气动特性研究[C]//2014年中国工程热物理学会工程热力学与能源利用、热机气动热力学和流体机械学术会议.北京:中国工程热物理学会, 2014:147093.

[5]王晓雷, 毋炳鑫, 吴必瑞. 风力机的新型变桨距自抗扰控制系统[J].动力工程, 2009, 29(3): 250-253.

WANG Xiaolei, WU Bingxin, WU Birui. A new active disturbance rejection variable pitch control system of wind turbine[J].Journal of Power Engineering,2009, 29(3): 250-253.

[6]沈昕.水平轴风力机气动性能预测及优化设计[D].上海：上海交通大学, 2014.

[7]QIU Yongxing, WANG Xiaodong, KANG Shun,etal. Predictions of unsteady HAWT aerodynamics in yawing and pitching using the free vortex method[J].Renewable Energy, 2014, 70: 93-106.

[8]NIEBSCH J, RAMLAU R, NGUYEN T T. Mass and aerodynamic imbalance estimates of wind turbines[J]. Energies, 2010, 3(4): 696-710.

[9]刘雄, 李钢强, 陈严, 等. 水平轴风力机叶片动态响应分析[J].机械工程学报, 2010,46(12): 128-134.

LIU Xiong, LI Gangqiang, CHEN Yan,etal.Dynamic response analysis of the blade of horizontal axis wind turbines[J].Journal of Mechanical Engineering,2010, 46(12): 128-134.

[10]李德源, 刘胜祥, 黄小华.大型风力机筒式塔架涡致振动的数值分析[J].太阳能学报,2008,29(11):1432-1437.

LI Deyuan, LIU Shengxiang, HUANG Xiaohua. Numerical analysis of vortex-induced vibration of the large scale wind turbine cylindrical tower[J].Acta Energiae Solaris Sinica,2008,29(11):1432-1437.

[11]CHATTOT J J, BRAATEN M E. Wind turbine pitch change simulation with helicoidal vortex model[C]//ASME Turbo Expo 2012: Turbine Technical Conference and Exposition. Copenhagen, Denmark:2012:789-796.

[12]PATRICK J. Aerodyn theory manual[M].Golden, Colorado,USA: National Renewable Energy Laboratory,2005.

[13]JONKMAN J M, BUHL J M L. FAST user's guide[M]. Golden, Colorado,USA:National Renewable Energy Laboratory, 2005.

[14]MANWELL J F, MCGOWAN J G, ROGERS A L. Wind energy explained: theory, design and application[M]. Manhattan,USA:John Wiley & Sons, 2010.

[15]HAND M M, FINGERSH L J, JAGER D W. Unsteady aerodynamics experiment phases II-IV test configurations and available data campaigns[M].Golden, Colorado,USA: National Renewable Energy Laboratory, 1999.

[16]YOUNSI R, ISMAIL E B, TRITSCH J B,etal. Dynamic study of a wind turbine blade with horizontal axis [J]. European Journal of Mechanics-A/Solids, 2001, 20(2)：241-252.

Influence of Structural Elasticity on Aerodynamic Performance of a Wind Turbine During Pitching Step

LIUChong,LIUPengyin,SHENXin,ZHUXiaocheng

(School of Mechanical Engineering, Shanghai Jiaotong University, Shanghai 200240, China)

Abstract：Numerical simulations were conducted on aerodynamic performance of a wind turbine during pitching step, while the effects of blade asymmetry, blade elasticity and tower elasticity on aerodynamic performance of the wind turbine were analyzed, and the overshoot phenomenon of turbine aerodynamic performance occurring in pitching step was simulated. Results show that the mass imbalance of two blades is the main reason leading to the rotor torque vibration before and after pitching step, and the structural elasticity of blade structure aggravates the rotor torque oscillation during overshoot. The fluctuation of axial thrust is caused by combined action of the imbalanced rotor, the elastic blade and tower structure, etc.

Key words：wind turbine; aerodynamic performance; pitch angle; flexible blade; flexible tower; numerical simulation

收稿日期：2015-07-20

修订日期：2015-09-30

基金项目：教育部博士点基金资助项目(20110073110031)

作者简介：刘翀(1990-)，女，黑龙江哈尔滨人，硕士研究生，主要从事风力机气动方面的研究.电话(Tel.): 18818251205;

文章编号：1674-7607(2016)06-0468-05中图分类号：TK83

文献标志码：A学科分类号：470.40

E-mail: chong_liu@sjtu.edu.cn.