3×3棒束通道内低速流动沸腾传热特性的实验研究

周云龙，　张　超，　李洪伟,　杨　迪，　侯延栋

(东北电力大学 能源与动力工程学院，吉林省吉林市 132012)



3×3棒束通道内低速流动沸腾传热特性的实验研究

周云龙，张超，李洪伟,杨迪，侯延栋

(东北电力大学 能源与动力工程学院，吉林省吉林市 132012)

摘要：以去离子水为实验介质，在入口温度为80～100 ℃、质量流速为0～100 kg/(m2·s)、入口压力为0.1 MPa的参数范围内，对棒束通道内流动沸腾传热特性进行了实验研究，分析了质量流速和热流密度对流动沸腾传热系数的影响，考察不同子通道内的传热特性.根据实验工况选取了Liu-Winterton关系式、Kandlikar关系式、Gungor-Winterton关系式和Chen关系式对棒束通道内的流动沸腾传热系数进行预测，将实验结果与预测结果进行比较，并对4个关系式的预测结果进行统计评估.结果表明：Liu-Winterton关系式、Kandlikar关系式和Chen关系式的预测结果偏小，其中Chen关系式的预测结果误差最大，Gungor-Winterton关系式的预测结果更加准确.

关键词：棒束通道； 流动沸腾； 热流密度； 传热特性

在压水堆(PWR)和沸水堆(BWR)发生失水事故时，冷却剂流过堆芯燃料棒束组件时就会出现棒束通道内的流动沸腾现象[1-2].然而，受到棒束通道特殊几何结构的影响，流体流过棒束通道时的流型、传热特性与流过普通圆管时存在显著差异，其传热机理尚未得到令人满意的理论分析结果.因此，研究棒束通道内的流动和传热，对核反应堆的设计和安全有效运行有着重要意义.

Anklam等[3]采用8×8的棒束在压力为3.9～8.1 MPa、水的流速小于0.01 m/s情况下进行了蒸汽-水的气液两相流实验研究，并对Zuber和Findlay在1965年提出的漂移流模型进行修正，得出了新的预测空泡份额的经验关系式.Osakabe等[4]在高压沸腾条件下对25根加热棒构成的棒束通道内的弹状流到环状流的转变进行了试验研究，提出了一个预测弹状流到环状流转变界限的模型.Qazi等[5]在圆形套管(水力直径DC=40 mm)内采用2×2的棒束进行了蒸汽-水的两相流试验，并对棒束间的流型进行了研究.Bergles等[6]在高压条件下采用蒸汽-水对正方形阵列的4根纵向棒束内的两相流流型进行了研究，得出纵向棒束通道内的流型及流型转变图.Wang等[7]在23～28 MPa的超临界压力范围内，采用水作为介质对2×2棒束内的流动沸腾传热特性进行了实验研究，分析了热流密度、系统压力和质量流速对棒束通道内水流动沸腾的影响，得到圆周方向的壁面温度分布，并将获得的实验数据与8个针对超临界水发展的传热关系式进行对比.赵桂生等[8]将R113作为实验工质，在内径为30 mm和35 mm的套管内对2×2棒束进行了过冷和饱和沸腾的研究，得出了管束间狭窄通道内传热系数与压降的经验关系式.

笔者通过对棒束通道内的流动沸腾传热特性进行实验研究，得到大量的实验数据，分析了质量流速、热流密度对棒束通道内流动沸腾传热特性的影响，选取Liu-Winterton关系式[9]、Kandlikar关系式[10]、Gungor-Winterton关系式[11]和Chen关系式[12]对传热系数进行预测,并与实验结果进行对比，研究结果可以为工程设计和相关设备的安全运行提供参考.

1实验装置及数据处理

1.1实验装置

纵向棒束气液两相流实验系统如图1所示，主要由水箱、离心泵、涡轮流量计、预热器、实验段、汽水分离装置、冷凝器和高速摄像仪等组成.实验选定去离子水作为工质，用离心泵驱动，经过预热器预热达到预定的入口温度后进入实验段.实验过程中，交流电直接加到预热段和实验段加热棒束，加热功率通过调压器连续调节.

实验段由电加热棒束和套管2部分组成，如图2所示.9根3×3阵列的不锈钢加热棒置于圆形套管中构成实验通道.加热棒束总长1 000 mm，底部300 mm 和顶部100 mm为非加热段，中间600 mm 为有效加热段；加热棒外径为10 mm，相邻棒间距为15 mm.套管长为1.33 m，外径为70 mm，内径为60 mm.

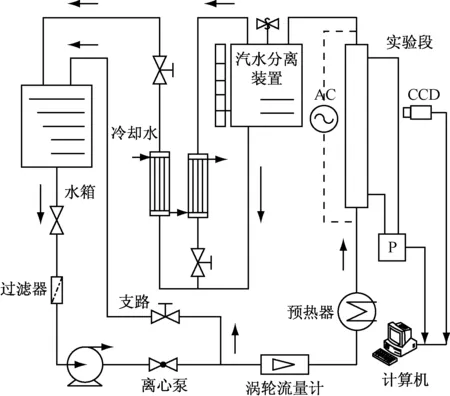
图1　实验流程图

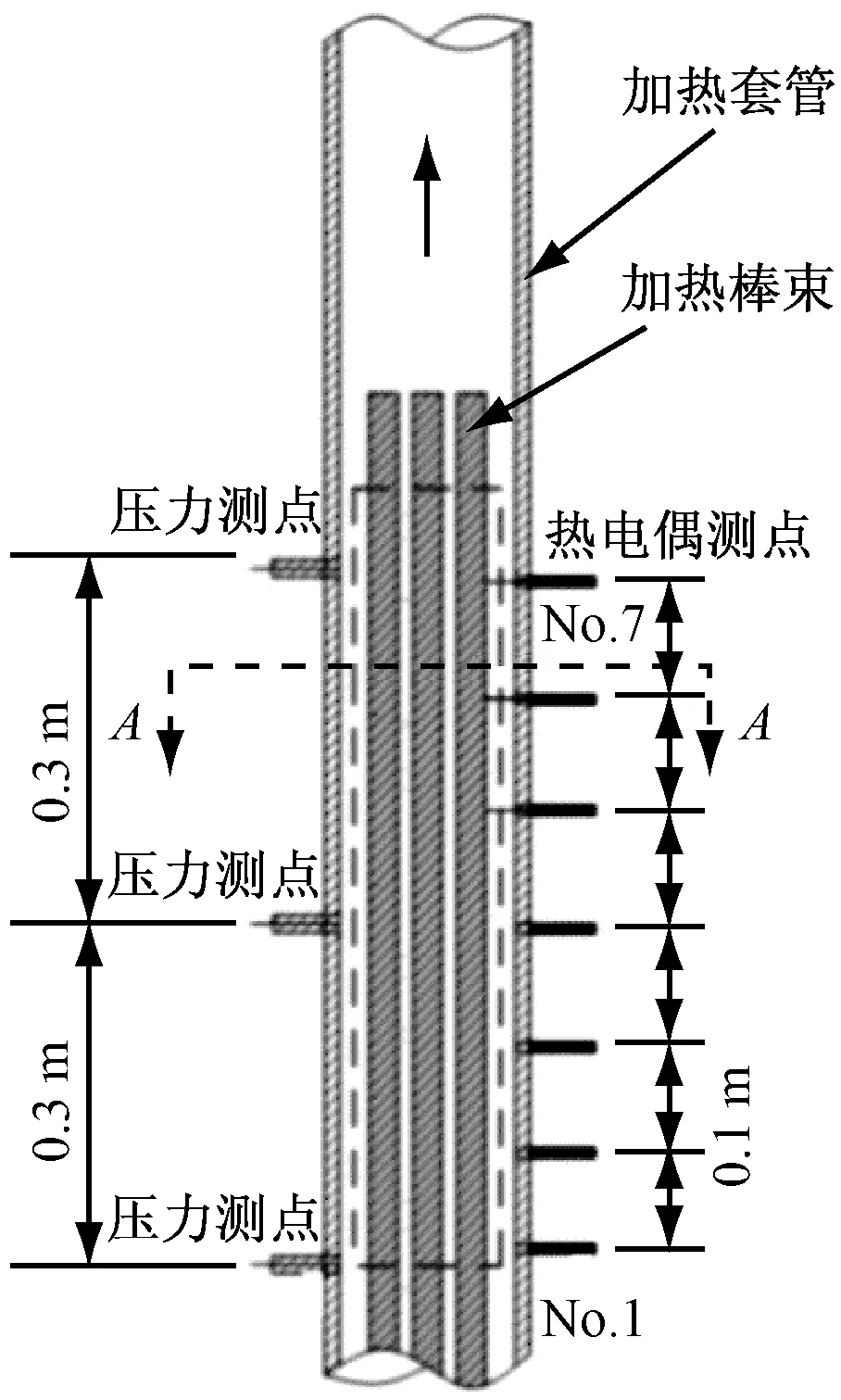
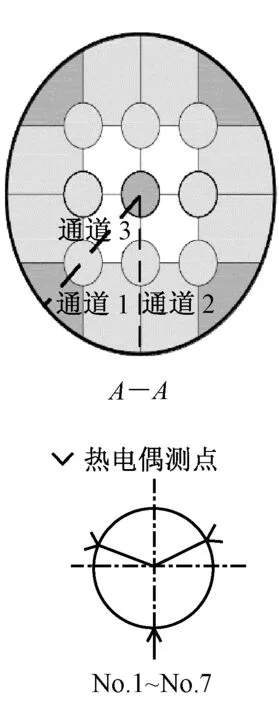
图2　实验段结构图

工质流量采用涡轮流量计测量，压力采用Rosemount 3051S电容式压力传感器测量，测量精度为0.05%.预热段和实验段的有效电加热功率根据测得的电压值和电流值计算得到.本实验中所有温度均采用K型热电偶测量.实验段共有7个测温截面，每个测温截面距离流体入口的距离分别为300 mm、400 mm、500 mm、600 mm、700 mm、800 mm和900 mm，每个测温截面Z上在加热棒外壁面设3个测温点，用来测量对应的3个局部壁面温度，测温点布置在离子通道1最近的加热棒上.实验段上共开3个测压孔，分别距入口300 mm、600 mm和900 mm.此外，在实验段对应的套管位置上，开2个对称的视镜口，镶嵌上石英玻璃(如图2中虚线方框所示)，在实验过程中用于高速摄影装置拍摄流型.

实验条件为：实验段出口压力为0.1 MPa，实验段流体入口温度为80～100 ℃，质量流速为0～100 kg/(m2·s).

1.2数据处理

根据Fluke万用表测得的电压值和电流，根据式(1)计算实验段的热流密度qe.

(1)

式中：Ue为实验段电源的电压，V；Ie为实验段电源的电流, A；d为加热棒直径,m；l为加热棒有效加热长度，m；ηe为实验段的加热效率，可在实验系统的热平衡实验中获得.

测温截面Z处的平均壁面温度计算如下：

(2)

式中：tw,z为测温截面Z处的平均壁面温度，℃；t1,z、t2,z和t3,z分别为测温截面Z处不同测点的温度，℃.

在测温截面Z处的传热系数为

(3)

式中：tf,z为测温截面Z处的流体温度，℃.

由于整个实验在过冷流动沸腾状态中进行，所以根据热平衡得到流体温度的计算公式为

(4)

式中：cp为比定压热容，kJ/(kg·K)；z为有效传热面积的轴向距离，m；G为质量流速，kg/(m2·s)；Ac为流通截面积，m2.

根据能量守恒，实验段和预热器的蒸汽干度计算公式如下：

(5)

式中：xin为实验段入口的干度;hf,z为测温截面Z处流体的焓值，kJ/kg;hf,in为入口流体的焓值，kJ/kg;hfg为汽化潜热，kJ/kg.

通过选取ζMAE(平均绝对误差)和ζRMSE(均方根误差)2个物理量对实验数据进行误差分析，计算公式如下：

(6)

(7)

式中：hcal为传热系数的经验关系式预测结果，W/(m2·K)；hexp为传热系数的实验结果，W/(m2·K).

2实验结果及分析

2.1质量流速对传热系数的影响

图3给出了质量流速G为12.5～13.4 kg/(m2·s)、36.8～37.8 kg/(m2·s)、52.4～53.2 kg/(m2·s)3种不同工况下传热系数h随干度变化的分布情况.从图3可以看出，当干度x<0.15时，3种质量流速下随着干度的增加传热系数增大，但差别很小；当干度x>0.15时，3种质量流速下的传热系数均显著增大，质量流速对传热系数的影响显著.这是由于干度较大质量流速越大时，截面含有的气泡数量越多，流动沸腾换热效果增强，导致传热系数增大.

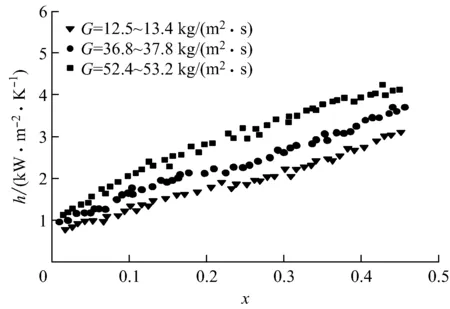
图3　干度对传热系数的影响

Fig.3Effect of dryness on heat-transfer coefficient at different mass flow rates

2.2热流密度对传热系数的影响

图4给出了系统压力p=0.1 MPa、质量流速G=24.6 kg/(m2·s)时，不同热流密度下两相流动区域内传热系数随干度的沿程分布情况.从图4可以看出，质量流速一定时，随着热流密度的增加，传热系数显著增大.这是由于x<0.5时，流型为泡状流、搅混流和环状流，泡核沸腾在流动沸腾换热过程中处于主导地位，从而导致传热系数增大显著.由于实验条件的限制，在实验中未出现干涸等情况，因此没有出现传热恶化、传热系数减小等情况.

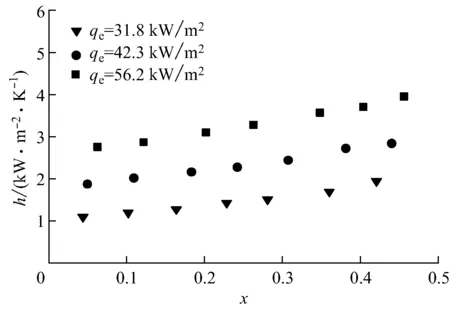
图4　热流密度对沸腾传热系数的影响

2.3各子通道内传热特性的分布

从图2可以看出，整个流动通道可划分为不同的子通道(子通道1～子通道3).不同子通道所处的位置不同，在通道内对流体的加热程度存在差异，造成不同通道内加热棒的壁面温度存在明显差异.图5给出了质量流速G=48.8～50.4 kg/(m2·s)情况下子通道内局部壁面温度tw的分布.从图5可以看出，子通道3内的壁面温度最低，子通道1内的壁面温度次之，子通道2内的壁面温度最高.这是由于不同子通道内的加热量、流通截面积以及流道形状存在差异，导致不同子通道内流体的搅混、流型及干度不同，导致子通道内壁面温度不同.

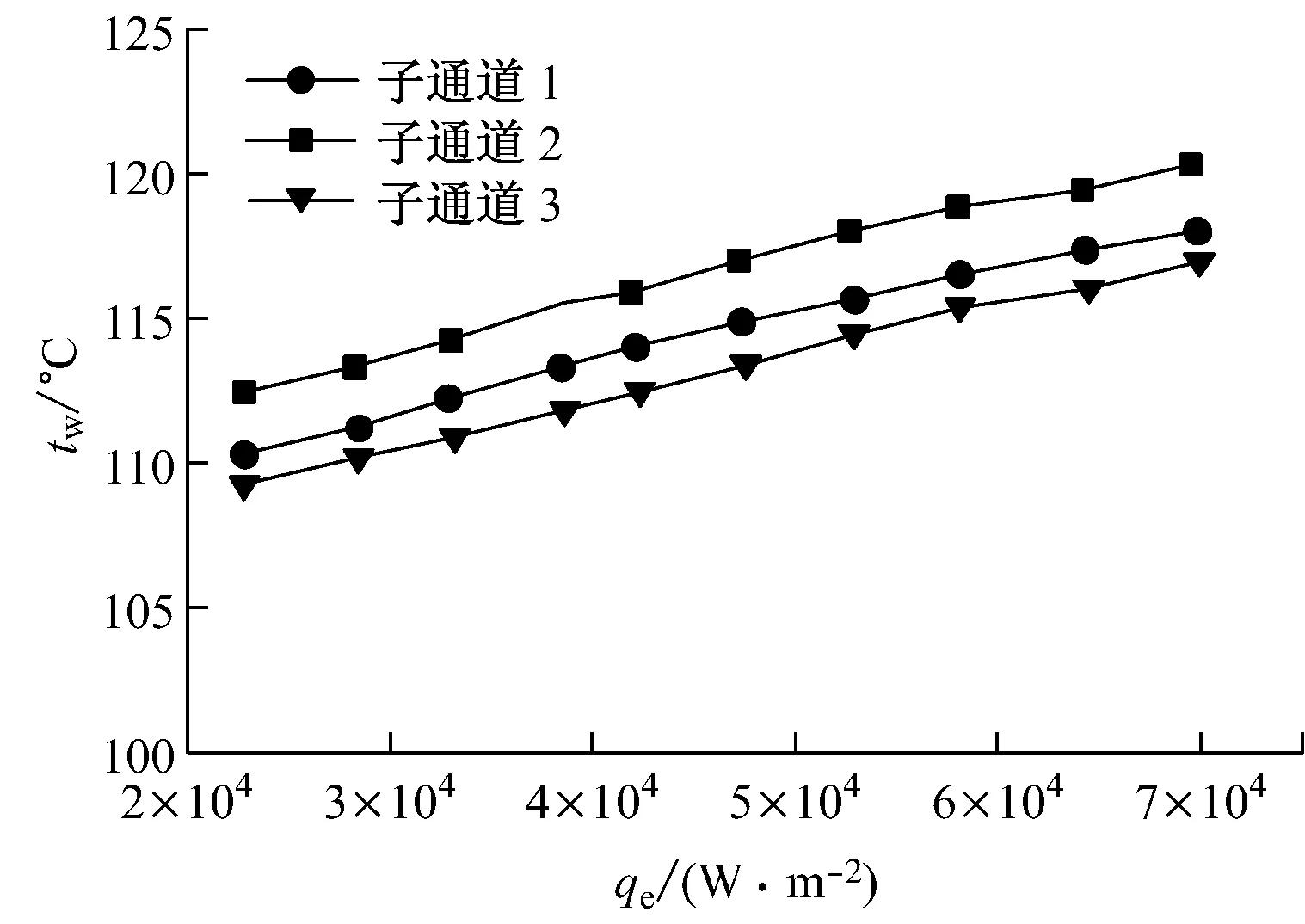
图5　子通道内局部壁面温度的分布

3与常用关系式的比较

3.1常用流动沸腾传热关系式

从已有文献看，目前针对圆通道、环形通道、矩形通道和微通道等已经提出了许多计算传热系数的经验关系式.其中Liu-Winterton关系式、Kandlikar关系式、Gungor-Winterton关系式和Chen关系式得到了较广泛的应用.上述4种关系式的具体形式见文献[9]～文献[12].其共同点都是将单相强制对流传热与核态沸腾传热相组合，根据干度的大小确定相关修正系数.本文的实验工况都处在上述关系式的范围内.

3.2各关系式预测结果与实验结果的比较

图6为本文的130个实验数据点与上述4种关系式预测结果的对比图.从图6可以看出，Liu-Winterton关系式、Kandlikar关系式和Chen关系式的预测结果偏小，Kandlikar关系式和Gungor-Winterton关系式的预测结果较准确.

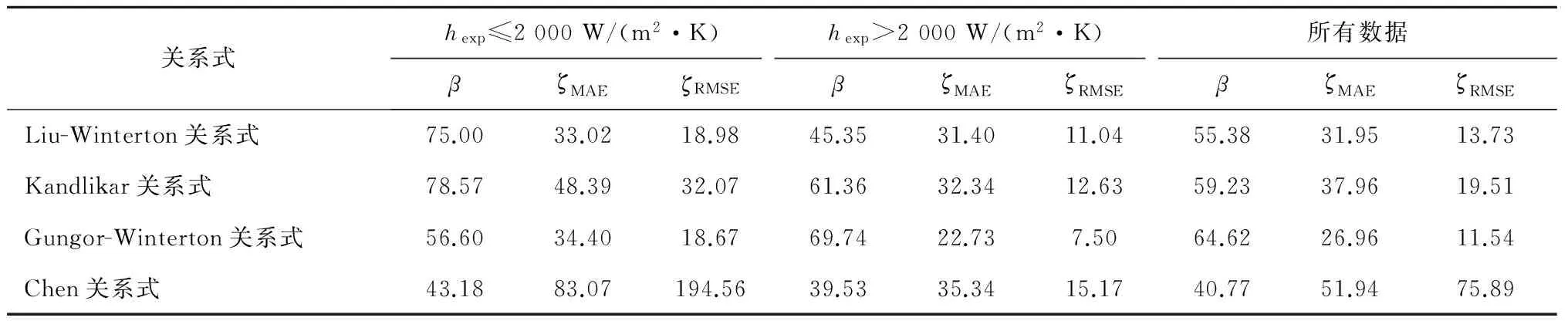
为了对预测结果有一个定量的分析，采用β(数据在±30%误差线内)、ζMAE和ζRMSE3个统计量对预测结果进行评价(见表1).从表1可以看出，当hexp≤2 000 W/(m2·K)时，Liu-Winterton关系式、Gungor-Winterton关系式预测结果的ζMAE、ζRMSE较小；当hexp>2 000 W/(m2·K)时，Gungor-Winterton关系式的β最大、ζMAE和ζRMSE最小.在整个实验工况范围内，Chen关系式的预测结果误差最大，Gungor-Winterton关系式的预测结果更准确.

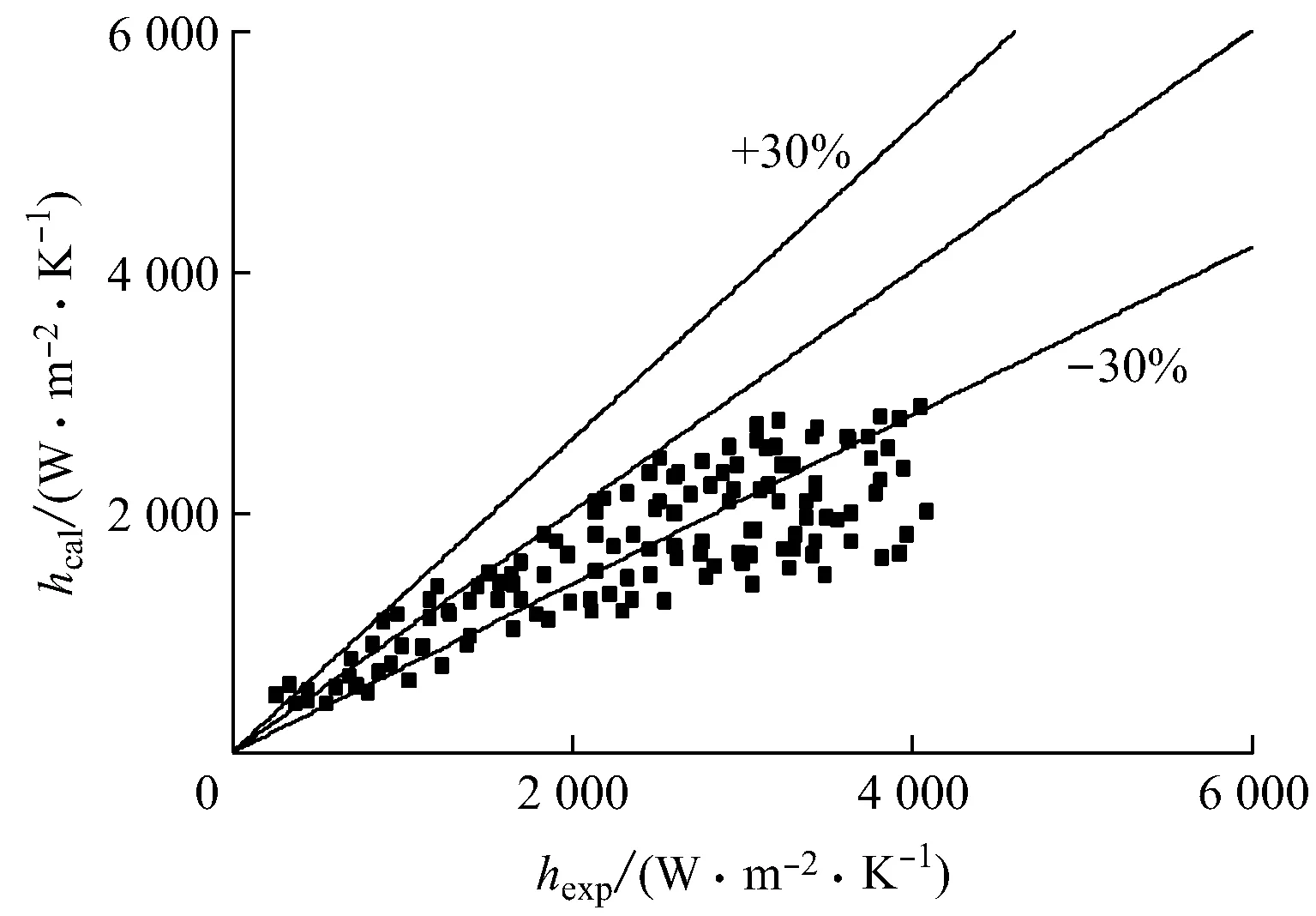
(a) Liu-Winterton关系式

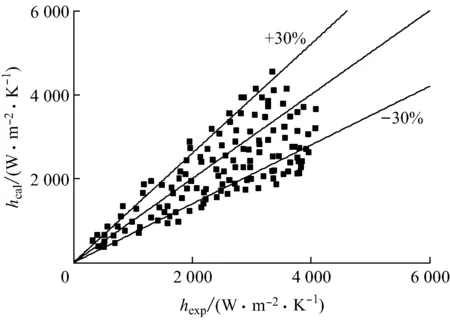
(b) Kandlikar关系式

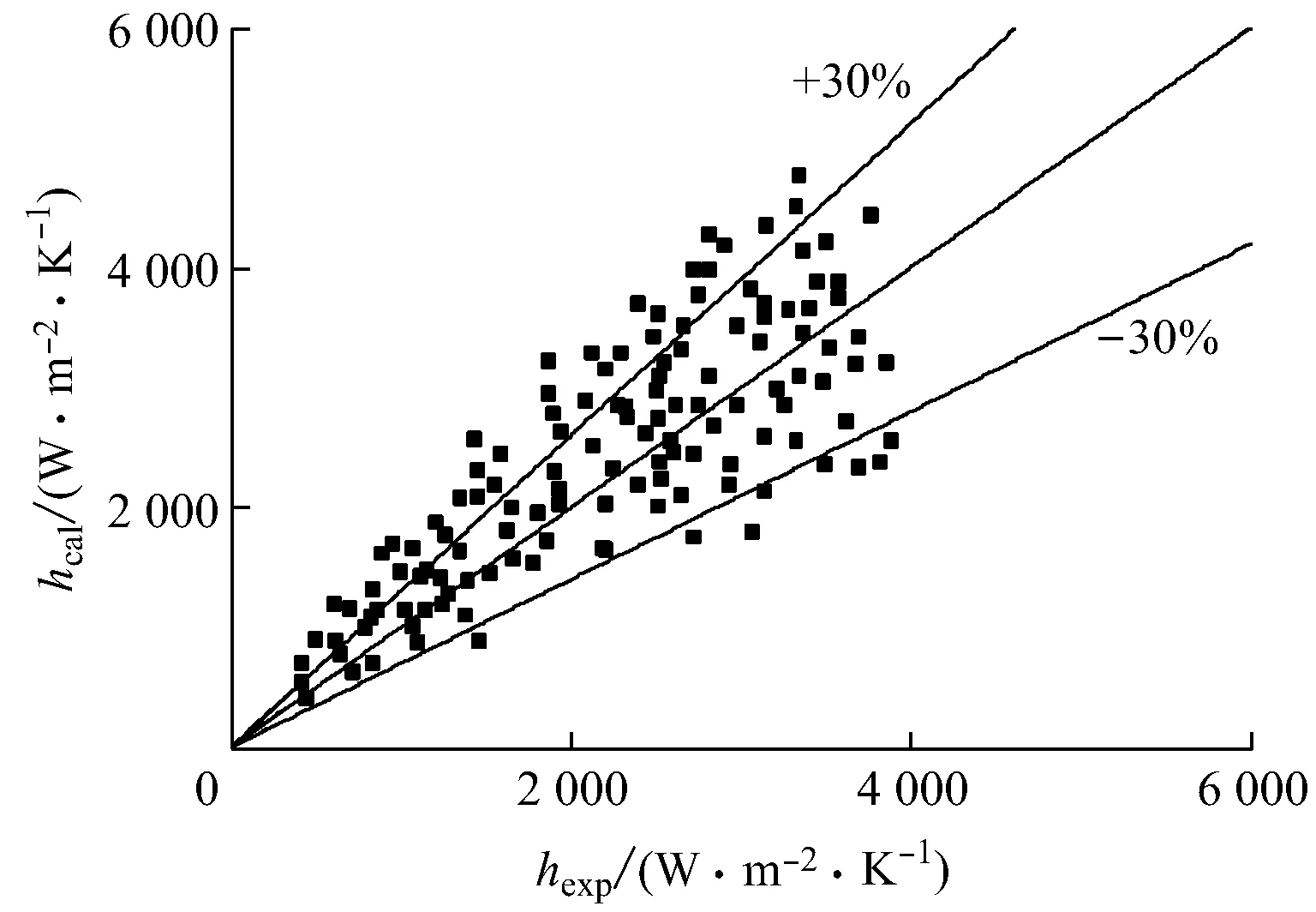
(c) Gungor-Winterton关系式

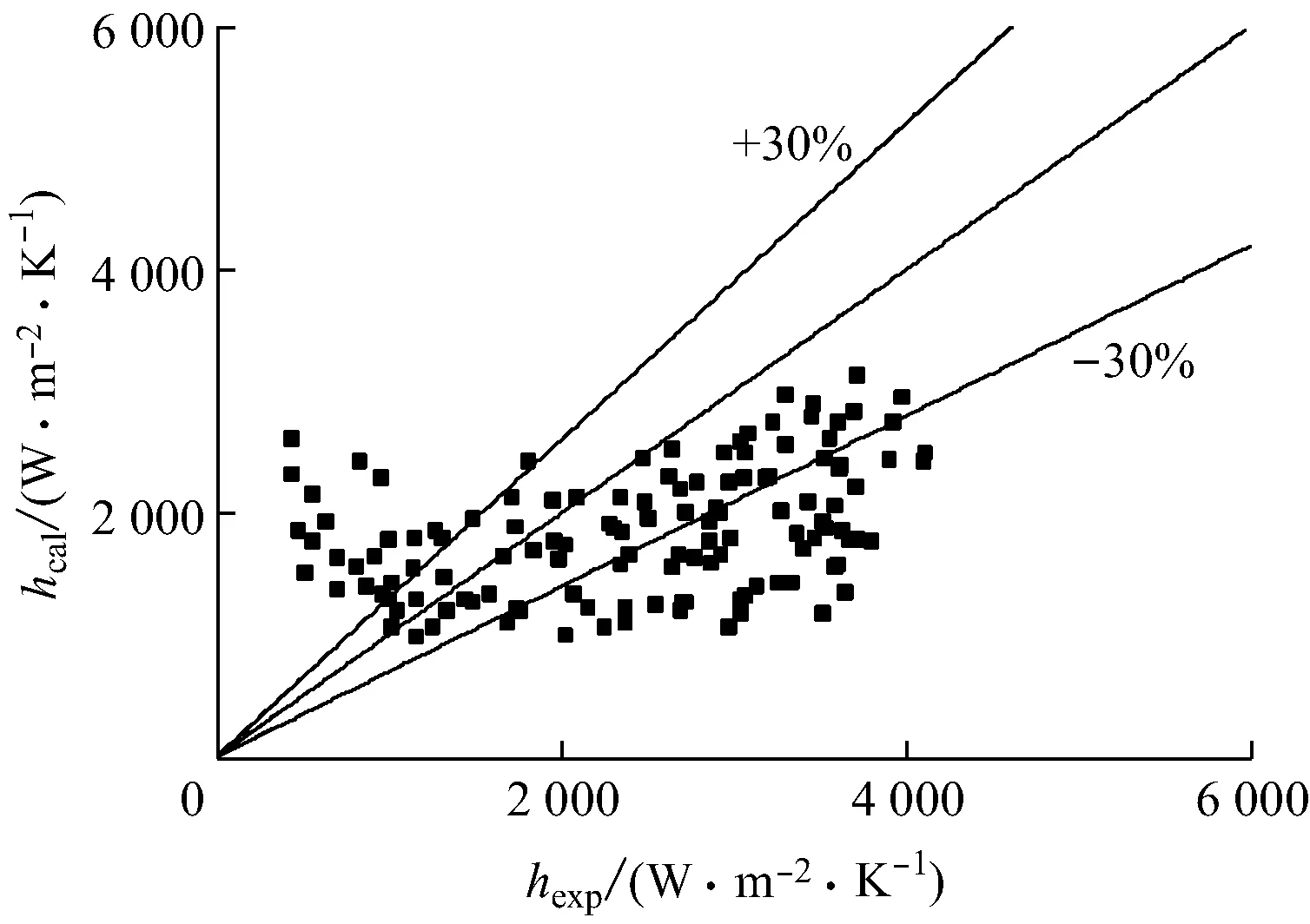
(d) Chen关系式

4结论

(1) 对棒束通道内流动沸腾传热特性进行了实验研究，分析了质量流速和热流密度对传热系数的影响.结果表明：当干度x<0.15时，3种质量流速下传热系数随着干度的增加增大，但差别很小；当x>0.15时，3种质量流速下的传热系数随着干度的增加显著增大，质量流速对其影响显著；质量流速一定时，随着热流密度的增加，传热系数显著增大.

(2) 当hexp≤2 000 W/(m2·K)时，Liu-Winterton关系式和Gungor-Winterton关系式预测结果的ζMAE、ζRMSE较小；当hexp>2 000 W/(m2·K)时，Gungor-Winterton关系式的β最大、ζMAE和ζRMSE最小；在整个实验工况范围内，Chen关系式的预测结果误差最大，Gungor-Winterton关系式的预测结果更准确.

参考文献：

[1]PETTIGREW M J, GORMAN D J. Vibration of heat exchanger tube bundles in liquid and two-phase cross-flow[J].Flow-Induced Vibration Design Guidelines,1981: 89-110.

[2]PETTIGREW M J, TAYLOR C E. Two-phase flow-induced vibration: an overview (survey paper)[J]. Journal of Pressure Vessel Technology,1994,116(3):233-253.

[3]ANKLAM T M, MILLER R F. Void fraction under high pressure, low flow conditions in rod bundle geometry[J].Nuclear Engineering and Design,1983,75(1):99-108.

[4]OSAKABE M, KOIZUMI Y, YONOMOTO T,etal. Slug to annular flow transition during boiloff in a rod bundle under high-pressure conditions[J].Nuclear Engineering and Design,1986,98(1):69-76.

[5]QAZI M K, GUIDO-LAVALLE G, CLAUSSE A. Void fraction along a vertical heated rod bundle under flow stagnation conditions[J].Nuclear Engineering and Design,1994,152(1/2/3):225-230.

[6]BERGLES A E, GOLDBERG P,CLAWSON L G,etal. Investigation of boiling flow regimes and critical heat flux[R]. Cambridge,Mass,USA: Dynatech Corp.,1968.

[7]WANG Han, BI Qincheng, WANG Linchuan,etal. Experimental investigation of heat transfer from a 2×2 rod bundle to supercritical pressure water[J].Nuclear Engineering and Design,2014, 275: 205-218.

[8]赵桂生,路广遥,王经.管束间狭窄通道单相及沸腾流动传热实验关系式[J].上海交通大学学报,2009, 43(2):266-270.

ZHAO Guisheng, LU Guangyao, WANG Jing. Experimental investigation of flow heat transfer correlation through tube bundle channel[J].Journal of Shanghai Jiaotong University,2009,43(2):266-270.

[9]LIU Z, WINTERTON R H S. A general correlation for saturated and subcooled flow boiling in tubes and annuli, based on a nucleate pool boiling equation[J]. International Journal of Heat and Mass Transfer, 1991,34(11): 2759-2766.

[10]KANDLIKAR S G. A general correlation for saturated two-phase flow boiling heat transfer inside horizontal and vertical tubes[J]. Journal of Heat Transfer,1990,112(1): 219-228.

[11]GUNGOR K E, WINTERTON R H S. A general correlation for flow boiling in tubes and annuli[J]. International Journal of Heat and Mass Transfer,1986,29(3):351-358.

[12]CHEN J C. Correlation for boiling heat transfer to saturated fluids in convective flow[J].Industrial & Engineering Chemistry Process Design and Development,1966,5(3):322-329.

Experimental Study on Low-velocity Flow Boiling Heat Transfer in a 3×3 Rod Bundle

ZHOUYunlong,ZHANGChao,LIHongwei,YANGDi,HOUYandong

(School of Energy and Power Engineering, Northeast Dianli University, Jilin 132012,Jilin Province, China)

Abstract：Taking deionized water as the working medium, experimental studies were conducted on flow boiling heater transfer in a 3×3 rod bundle at an inlet temperature of 80-100 ℃, a mass flow rate of 0-100 kg/(m2·s), and an inlet pressure of 0.1 MPa, so as to analyze the effects of mass flow rate and heat flux on the flow boiling heat-transfer coefficient, and to investigate the heat-transfer characteristics in various sub-channels. Four correlations were adopted to predict the flow boiling heat-transfer coefficient, including Liu-Winterton, Kandlikar, Gungor-Winterton and Chen, etc., and subsequently their prediction results were compared with experimental data, which were simultaneously evaluated using three statistic indicators. Results show that the predicted values of Liu-Winterton, Kandlikar, and Chen correlation are relatively lower than the experimental data, in which the error of Chen correlation is the highest, while Gungor-Winterton correlation is the most accurate one among all the four correlations.

Key words：rod bundle channel; flow boiling; heat flux; heat-transfer characteristic

收稿日期：2015-02-05

修订日期：2015-10-22

基金项目：国家自然科学基金资助项目(51406031)

作者简介：周云龙(1960-)，男，吉林松原人，教授，博士生导师，主要从事气液两相流与传热方面的研究.

文章编号：1674-7607(2016)06-0493-05中图分类号：TK212

文献标志码：A学科分类号：470.10

侯延栋(通信作者)，男，硕士研究生，电话(Tel.):13659251192;E-mail:houyandong1012@126.com.