柔性襟翼对风力机翼型气动性能的影响

郝文星，　叶　舟,2，　丁勤卫，　李　春,2

(1. 上海理工大学 能源与动力工程学院，上海 200093；2. 上海市动力工程多相流动与传热重点实验室，上海 200093)



柔性襟翼对风力机翼型气动性能的影响

郝文星1，叶舟1,2，丁勤卫1，李春1,2

(1. 上海理工大学 能源与动力工程学院，上海 200093；2. 上海市动力工程多相流动与传热重点实验室，上海 200093)

摘要：通过对柔性尾缘襟翼(DTEF)参数化建模，实现了对尾缘襟翼柔性变形与控制.采用数值模拟方法研究DTEF对翼型整体静态与动态气动性能的影响及流动机理.结果表明：DTEF位于不同摆角时，翼型升力系数与阻力系数均有不同程度的明显改变，随着攻角的增大，襟翼改变翼型气动性能的能力降低，对襟翼附近的流动影响亦减弱；DTEF动态运动过程中，翼型升力系数滞后于摆角的变化，DTEF改变升力系数的能力降低，翼型阻力系数超前于摆角的变化，DTEF改变阻力系数的能力增加，此动态效应随摆动周期减小而增强，并在翼型表面压力系数与尾迹涡量上有一定体现.

关键词：风力机翼型； 气动性能； 柔性襟翼； 计算流体力学

为了更大程度地获取风能，降低单位风电成本，风力机单机容量及叶片尺寸不断增长，截止至2014年，已研制出的风力机最大单机容量为10 MW，风轮直径达190 m，最大叶片尺寸达到85 m[1].叶片尺寸的增大使得叶片极限载荷和疲劳载荷增大，且使沿叶片展向载荷分布不均匀性增强[2].尾缘襟翼能够改变翼型的气动性能，在风力机运行过程中，通过控制其运动与几何特性实现对叶片的载荷控制，且能够克服现有变桨技术的大惯性以及不能有效控制局部载荷波动上的不足[3].

美国Sandia国家实验室、荷兰Delft理工大学和丹麦RisØ DTU等几个国外著名实验室较早地开展了风力机叶片尾缘襟翼的研究，初步结果表明尾缘襟翼具有较好的降载效果[4-5].Troldborg[6]以具有可变参数的尾缘襟翼RisØ-B1-18翼型为研究对象，基于数值模拟重点对尾翼形状和尺寸进行了优化，得出长度0.05c～0.1c(c为翼型弦长)的尾缘襟翼为较优设计方案.Lackner等[7]采用GH_BLADED对比分析了美国可再生能源实验室(NREL)5 MW风力机叶片分别采用独立变桨和尾缘襟翼后对疲劳载荷的影响，指出尾缘襟翼可有效降低叶片疲劳载荷.Andersen[8]采用HAWC2模拟动态失速模型和近尾流模型，验证了尾缘襟翼减少疲劳载荷的能力.Lackner等[9]对尾缘襟翼非定常特性进行了研究，并选取折合频率作为评价参数，如式(1)所示.

(1)

式中：l为特征长度；f为扰动频率；U为特征速度.以翼型弦长c为特征长度，流体流速为特征速度，主要扰动为襟翼运动，可较好地表征襟翼摆动频率.余畏等[10]自主开发了基于尾缘襟翼整机气动伺服弹性仿真平台，验证了湍流风况下襟翼减小叶片疲劳载荷的有效性.叶舟等[11]以襟翼摆角为控制变量，研究了尾缘襟翼对翼型升阻特性的控制效果以及其对翼型周围流场特性的影响.李传峰等[12]采用计算流体力学方法研究了尾缘襟翼偏转角频率对翼型气动参数及动态特性的影响，指出襟翼偏转达到一定角频率时流场具有明显的动态特性.

以上研究主要关注的是尾缘襟翼气动特性、控制策略和实现方式等方面，更多地考虑流动的宏观参数，较少考虑襟翼在静态和动态过程中对气动性能的不同影响及其影响机理.

笔者以NREL S809翼型[13]为基础翼型，通过控制襟翼参数实现襟翼几何变形与运动，利用计算流体力学(CFD)方法研究襟翼变形对翼型气动性能的影响，进而分析其影响机理，并对襟翼运动时的气动及流场动态特性进行分析.

1计算模型

1.1尾缘襟翼模型

图1给出了以S809为基础翼型的尾缘襟翼变形示意图.其中，H为变形铰点，坐标为(x0,y0)；θ为襟翼顶端相对基础位置摆动角度(定义逆时针为正).柔性尾缘襟翼型线变化规律如式(2)所示，通过对襟翼表面节点控制实现襟翼变形，θ′为型线各节点绕铰点H的偏转角度.函数f(x,q,x0)通过控制节点偏转角度随节点横坐标x的变化来控制襟翼摆动时的形状，为保证襟翼变形的连续性，f(x,q,x0)满足式(3).采取函数形式f(x,q,x0)=(x-x0)q，参数q用以调节襟翼型线的曲率变化.函数R(t)为襟翼摆动的时间函数，用于描述襟翼的位置随时间的变化.

影响尾缘襟翼型线的参数主要包括铰点位置(襟翼长度)、偏转角度和形状函数，襟翼摆动规律主要受时间函数影响，襟翼变形与控制模拟通过CFD软件二次开发端口实现.笔者主要讨论襟翼摆动对翼型气动性能的影响，参考Troldborg[6]的研究结果，定义襟翼长度为0.1c，最大偏转角θ为10°，形状参数q为1，此时襟翼外形过渡性较好，襟翼以正弦规律摆动，如式(4)所示.

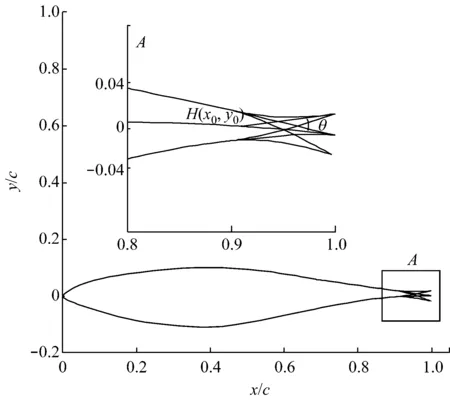
图1　尾缘襟翼变形示意图

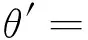
(2)

(3)

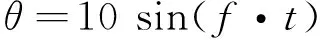
(4)

1.2计算域划分及网格

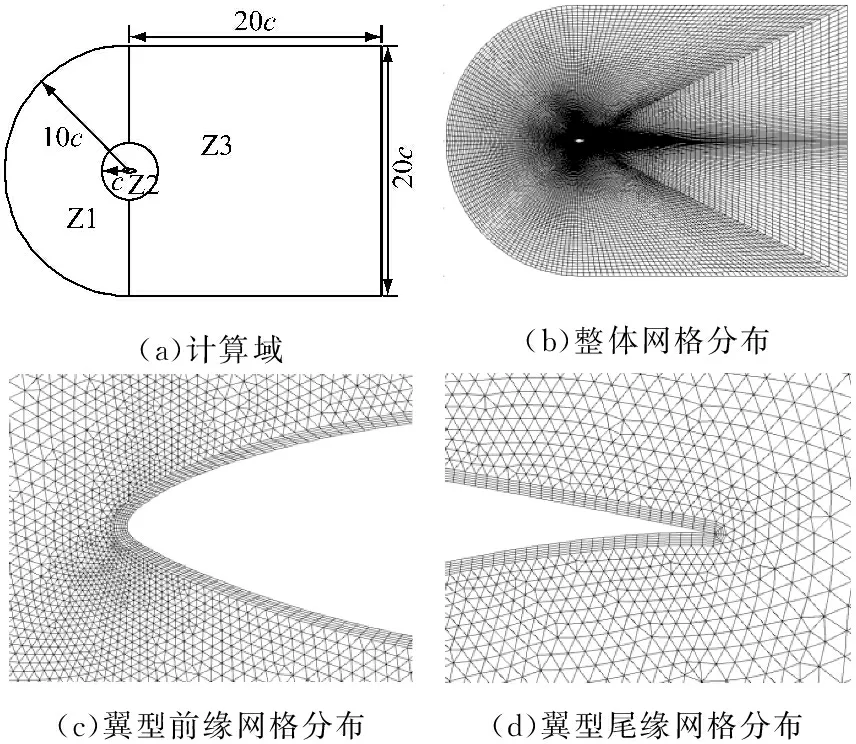
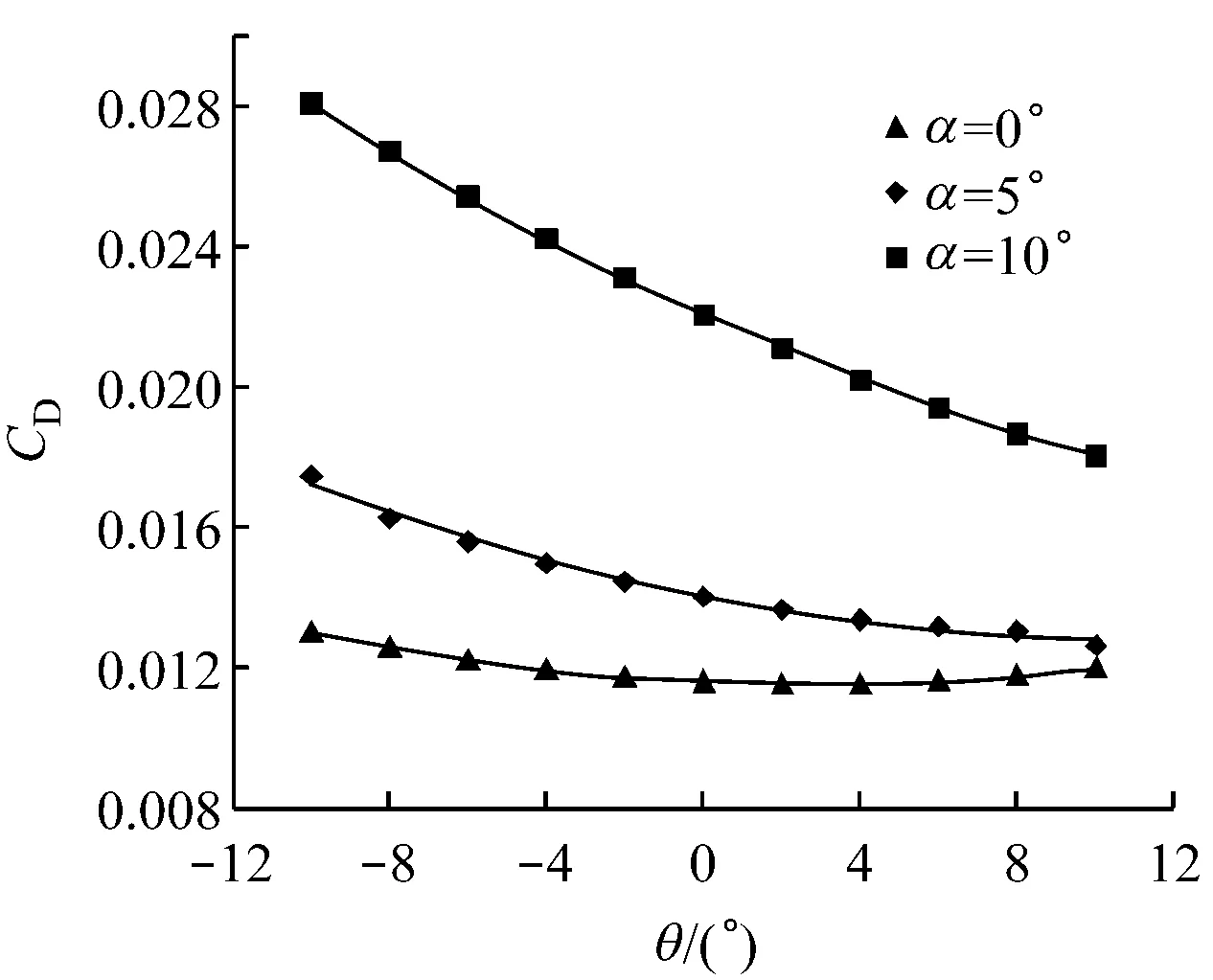
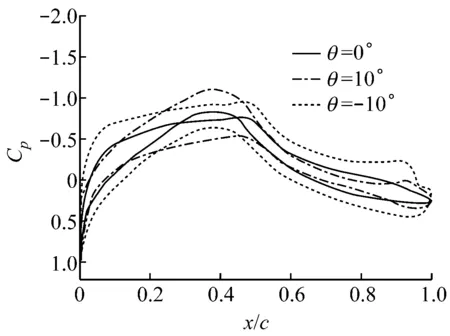
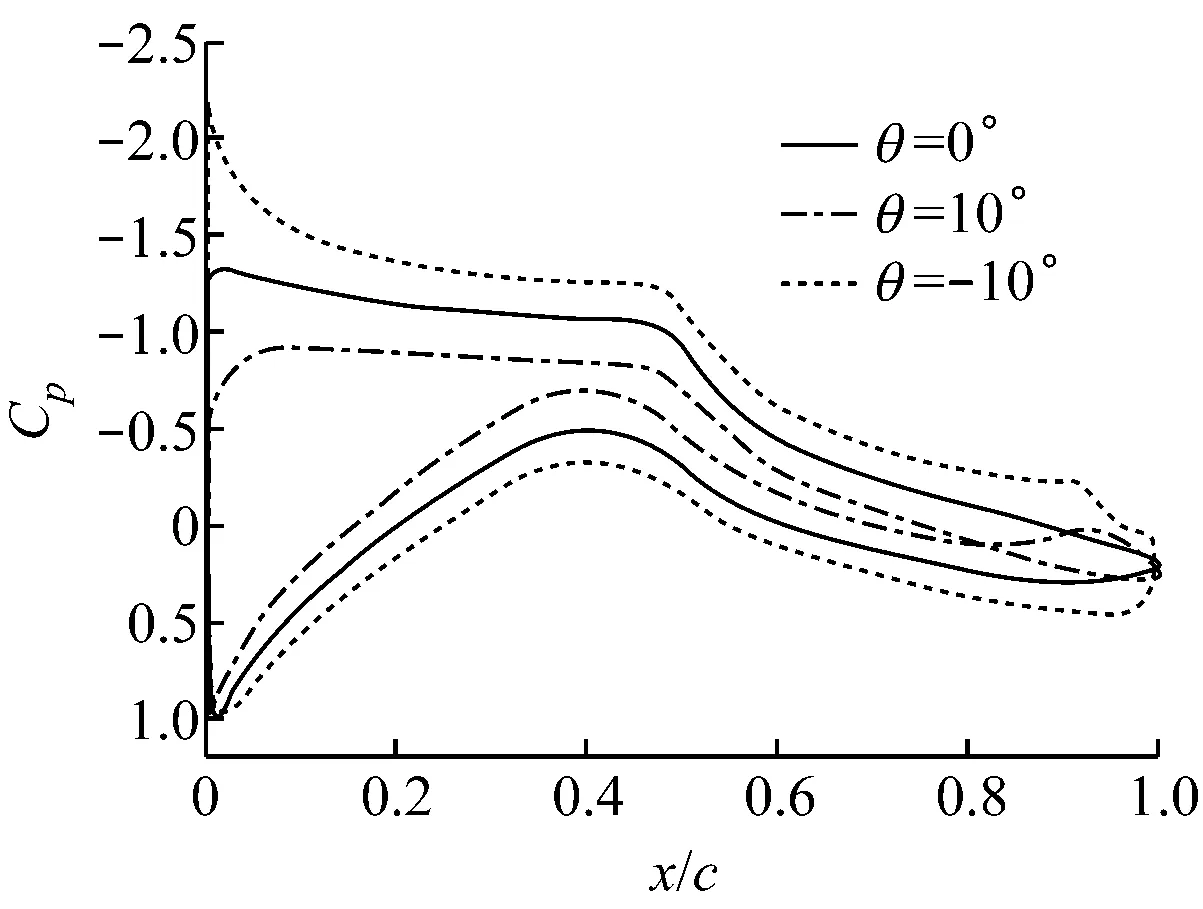
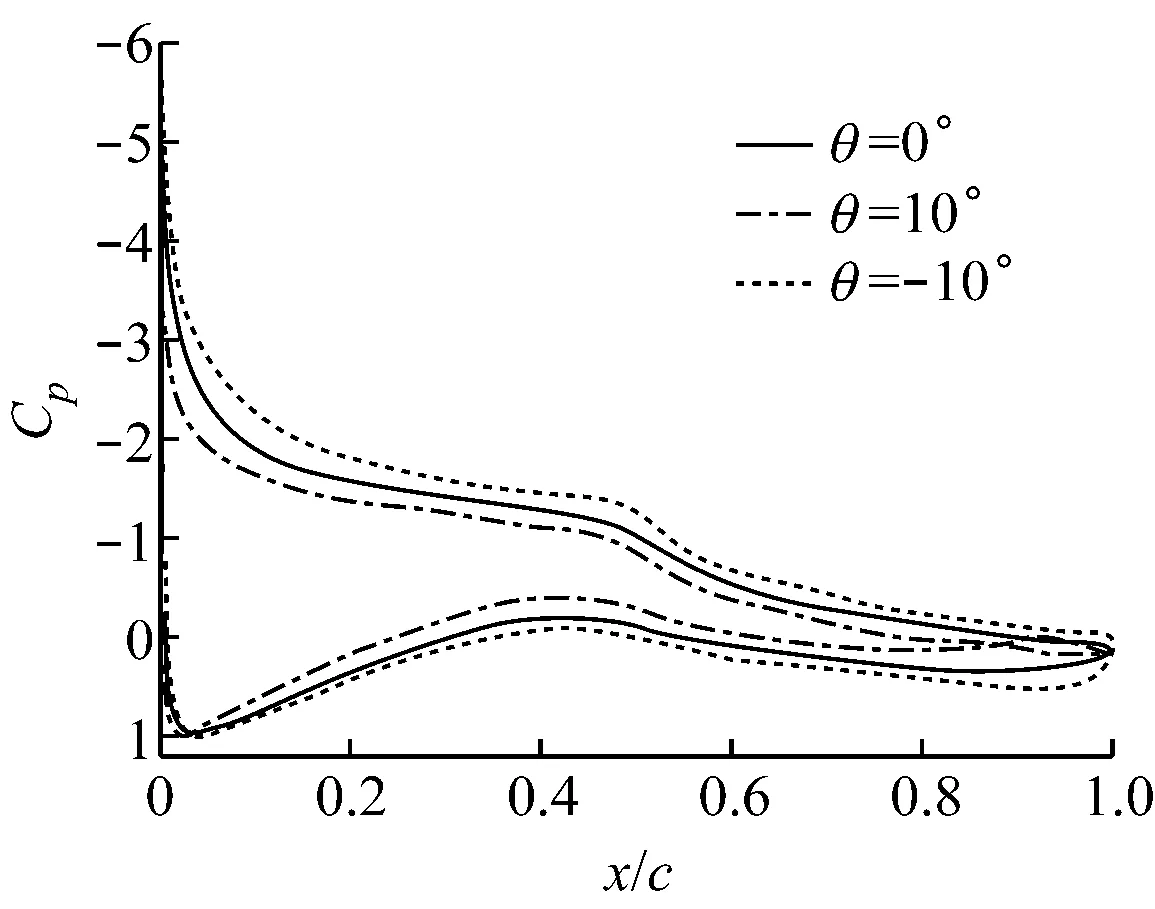
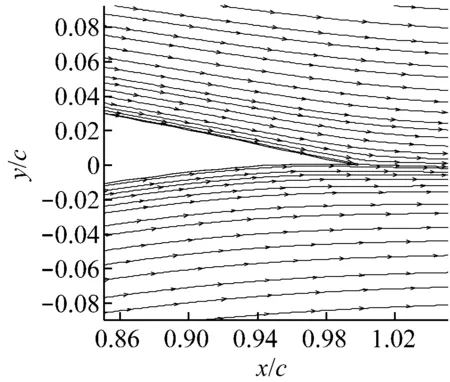
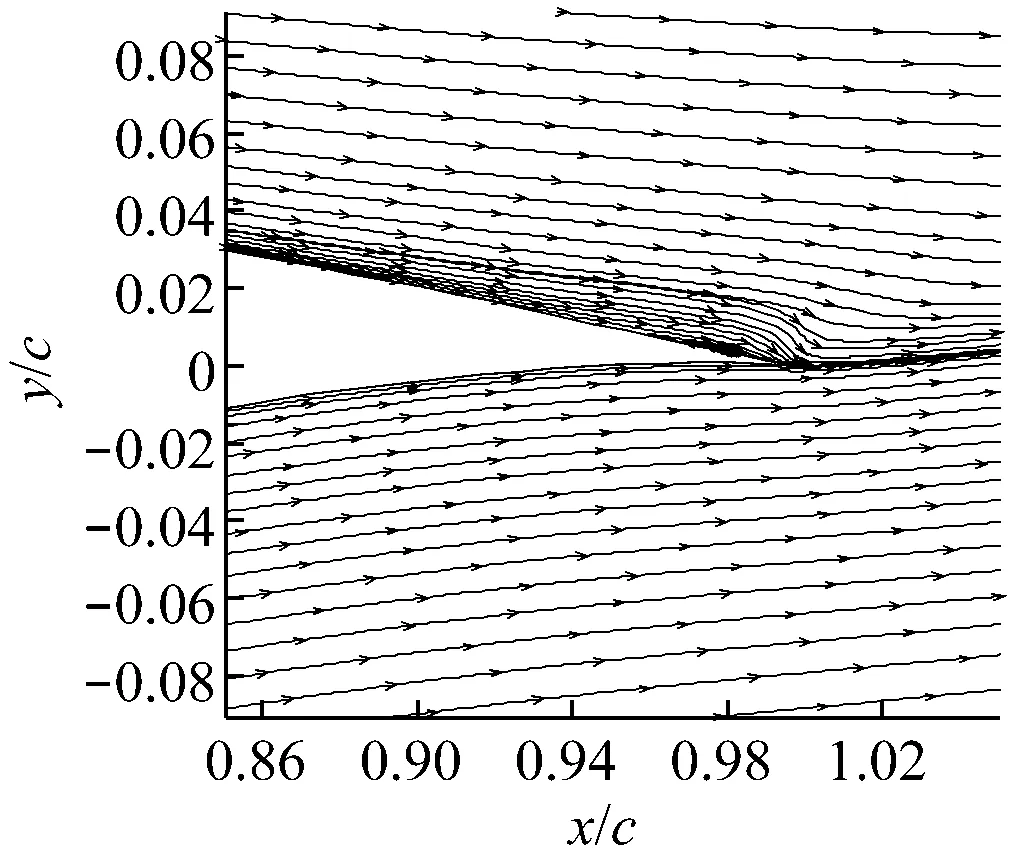
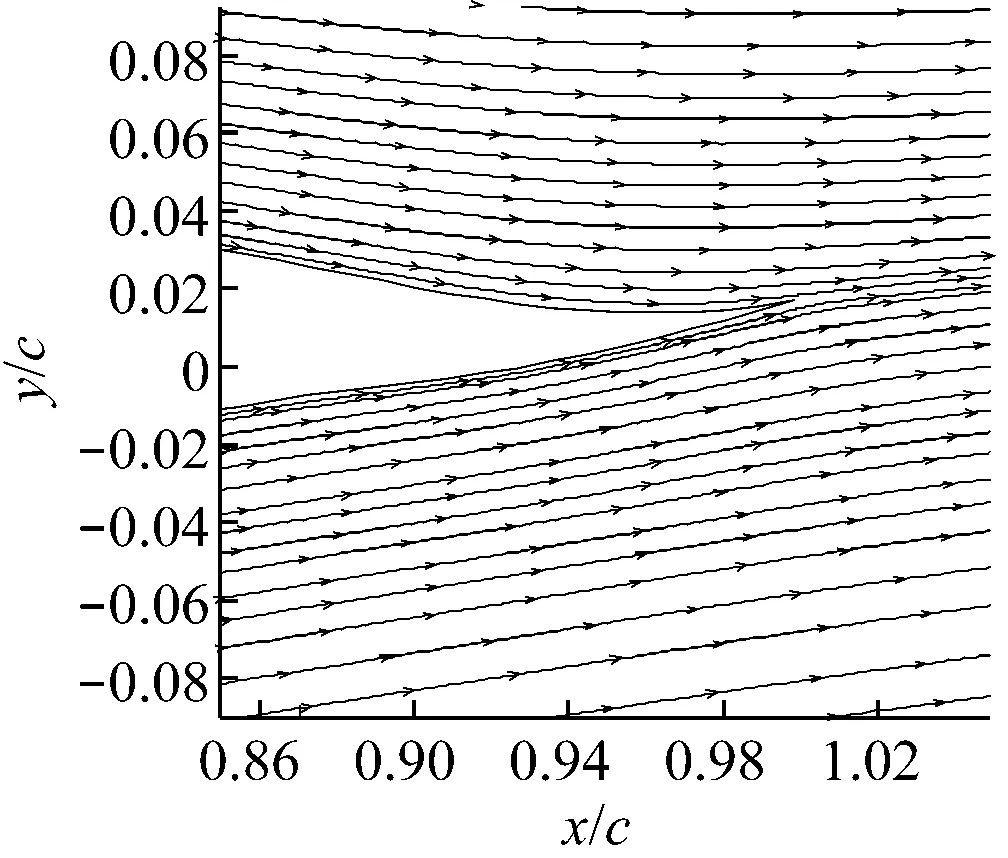
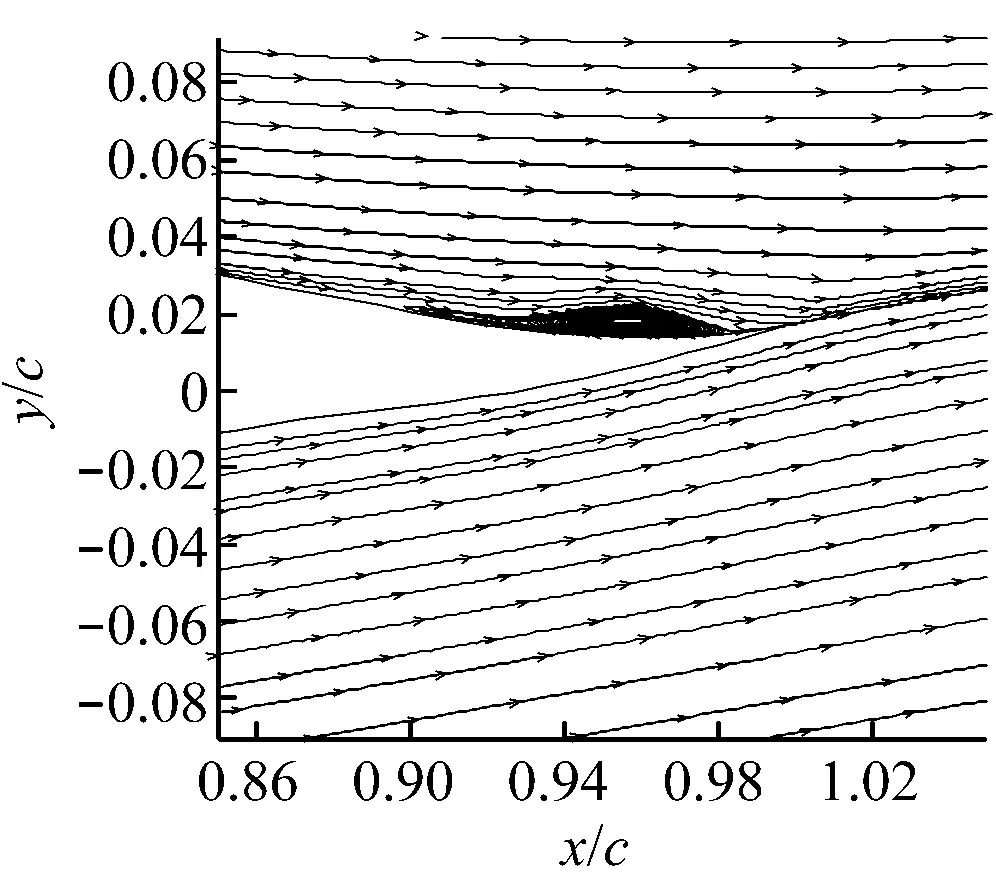
翼型计算域拓扑结构及襟翼周围网格分布如图2所示.计算域由上游来流区、动态网格区和下游尾迹区3部分组成，其中上游来流区Z1为半径10c的半圆形区域，下游尾流区Z3为边长20c×20c的正方形区域，动态网格区Z2为半径c的圆形区域.采用动网格技术[14]控制变形襟翼周围网格重构.常用的动网格技术包括以下3种：滑移网格技术、重构动网格技术和变形动网格技术.根据襟翼的摆动特点，采用重构动网格技术来实现网格变化.

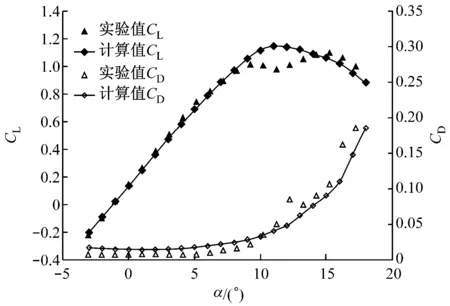
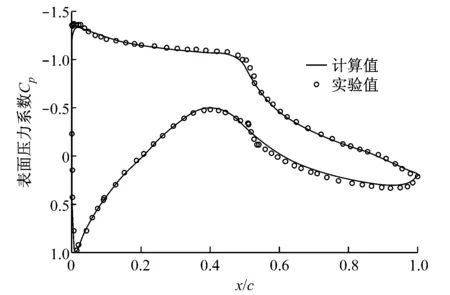
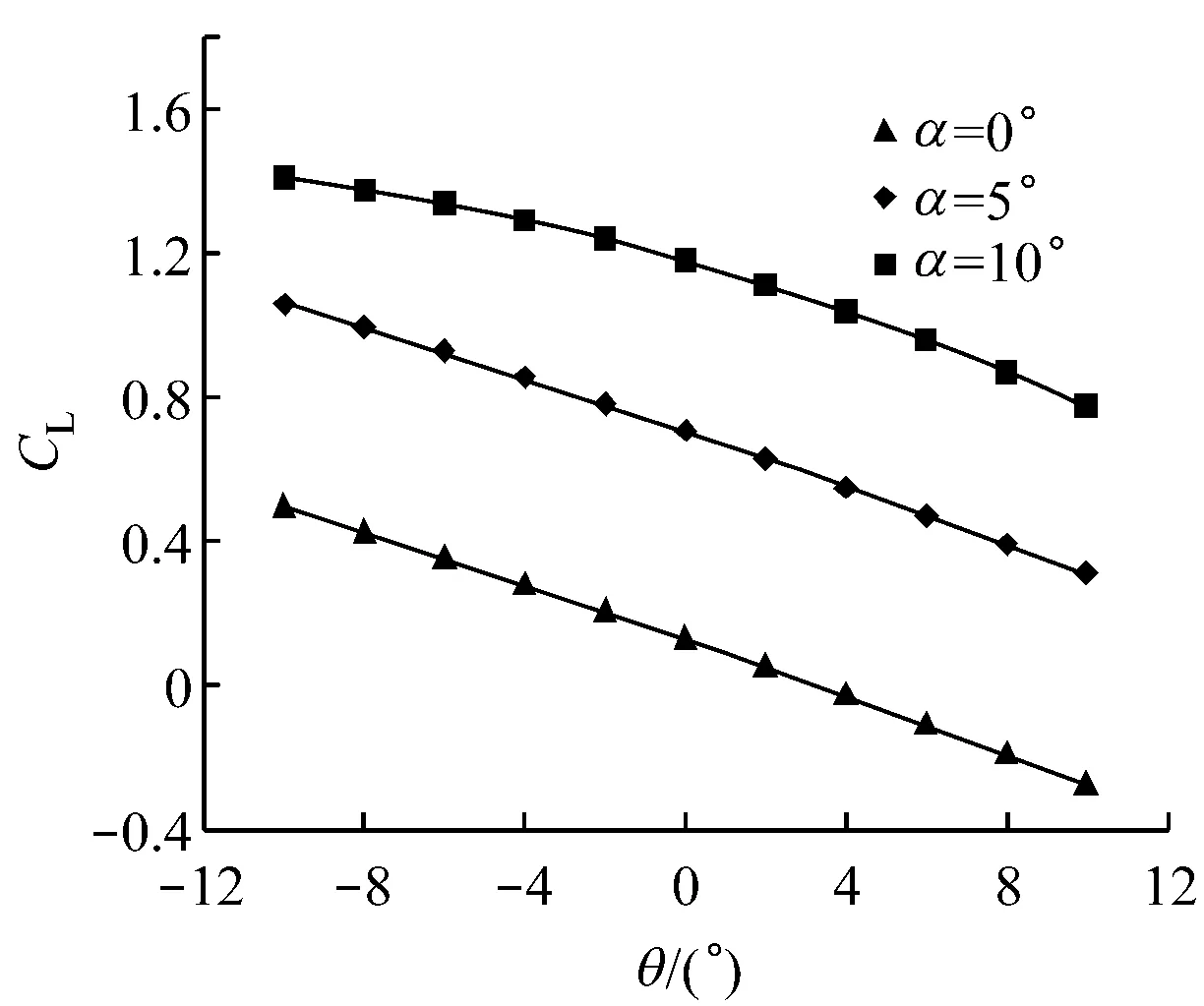
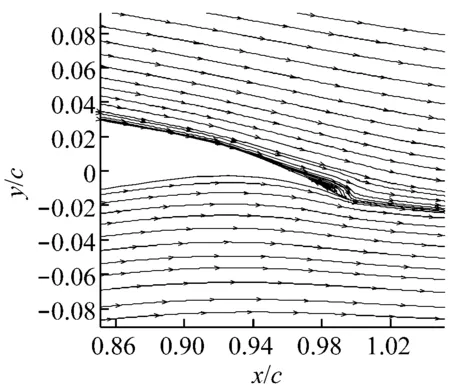
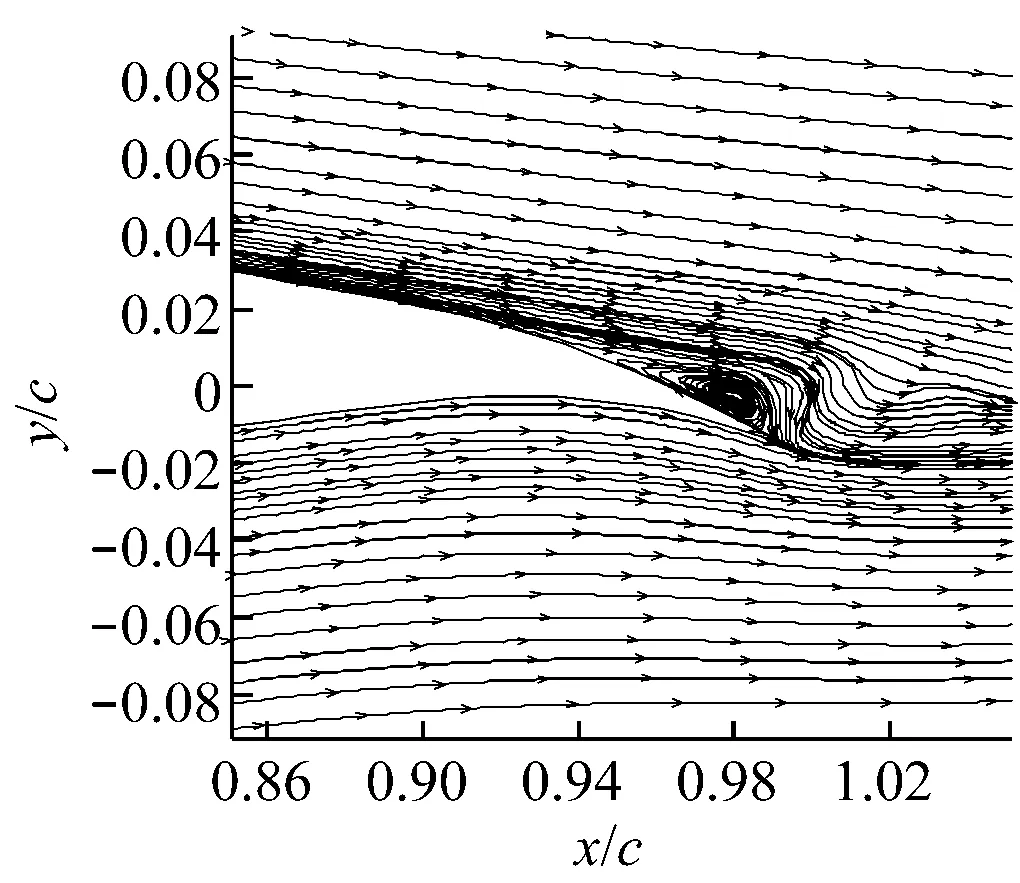
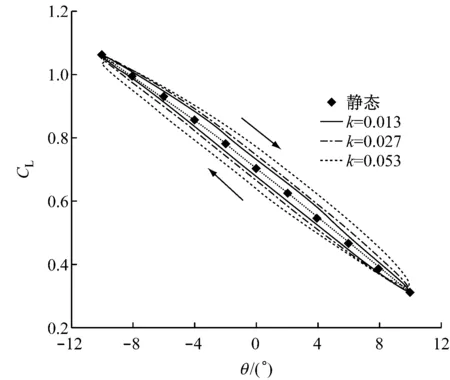
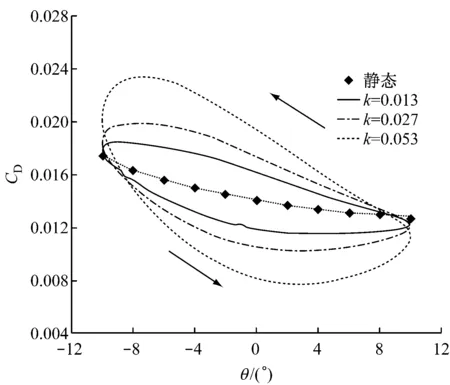
上游来流区与下游尾流区采用结构化网格，动态网格区采用三角形非结构网格.因网格重构过程中翼型周围新生成的网格质量会发生改变，为防止其影响计算精度，在翼型周围覆盖边界层网格.边界层网格不参与网格重构，采用与襟翼摆动相同的运动规律控制其随襟翼一起运动.网格总数约为30 000，翼型表面布置264个节点，对翼型前缘进行了加密处理，第一层网格中心距离壁面约为0.002c(30

(a)计算域(b)整体网格分布(c)翼型前缘网格分布(d)翼型尾缘网格分布

图2翼型计算区域及其网格分布图

Fig.2Calculation region and grid distribution of the airfoil

1.3湍流模型

采用湍流模型RNGk-ε模型进行数值求解，RNGk-ε模型将壁面流动假设为充分发展湍流，主要用于求解处于湍流核心区的流动，故将翼型表面网格放置于湍流核心区，采用标准壁面函数近似黏性底层与过渡层[16].流域入口边界类型为速度入口，来流雷诺数Re=2×106，出口条件设为压力出口，压强为环境压强，翼型表面设为固壁无滑移条件.因来流风速较小且不涉及传热等情况，将来流视为不可压，对连续性方程和动量方程进行求解，采用基于压力求解器，压力-速度耦合采用Simple算法.动态模拟无量纲时间步Δt*经无关性验证后设置为2.5×10-4，无量纲时间步的计算如式(5)所示.

(5)

式中：Δt为实际时间步；cf为襟翼长度；T为襟翼摆动周期.

2可行性验证

翼型主要气动性能参数包括翼型升力系数CL、阻力系数CD以及升阻比K等，如式(6)所示.

(6)

式中：FL为与来流方向垂直的力，即翼型的升力；FD为与来流方向平行的力，即翼型的阻力；ρ为空气密度;W为相对翼型来流风速.

为了验证上述模型对风力机翼型气动性能分析的可行性，选用S809翼型进行二维气动性能计算，并将计算结果与实验数据进行对比分析，实验数据来自TU-Delft的实验[12].攻角α的范围为-3°≤α≤18°.对比结果如图3所示.

从社会和国家层面来看，工匠精神是一种高层次的文化形态，是中国精神的重要内容之一，是社会主义核心价值观的生动体现，是国家和社会构建的价值观念和发展理念，是中华传统文化在国家战略上的支撑和灵魂。作为一种优秀的职业道德文化，它的传承和发展契合了时代发展的需要，具有重要的时代价值和社会意义。通过工匠精神的传承和发扬，新时代中国改革建设发展取得辉煌成就，使中国走向了世界舞台中央，为世界提供了中国智慧和中国方案。培育工匠精神既是实现中华民族伟大复兴中国梦的现实需要，也是高校附属医院党建思想政治教育及其理论研究的一项重要内容。

(a)气动性能参数

(b)α=5.13°时表面压力系数

由图3(a)可以看出：攻角为-3°～9°时，翼型主要位于附着流区[13]，升力系数的计算值与实验值吻合较好，其最大偏差均不超过5%；攻角大于9°时，翼型靠近尾缘绕流开始发生较大分离，因流动情况较为复杂且存在动态现象，计算值与实验值存在一定误差.阻力系数计算值在附着流区大于实验值，在失速区与实验值较为吻合.流体在翼型表面的流动过程为由层流到湍流的转捩过程[17]，上述模型将流动假设为全湍流，因此产生的模拟误差主要体现在附着流区阻力系数上.但因附着流区阻力系数值比较小，且整体模拟趋势较为吻合，故可以采用全湍流模型模拟翼型气动性能.

图3(b)给出了攻角为5.13°时翼型表面压力系数模拟值与实验值的对比.由图3(b)可以看出，此计算模型可较好地模拟翼型表面压力，各位置处表面压力系数计算值以及变化走势均与实验值较为吻合，对0.5c附近因上表面流体由层流向湍流转捩而导致此处压力升高这一现象也有较好的体现.通过对比分析可知，此CFD计算模型对于风力机翼型二维流动具有较高的模拟精度，可较好地模拟翼型气动性能以及翼型流场流动特点.

3结果分析

3.1静态气动性能

图4给出了攻角为0°、5°和10°时S809翼型气动性能参数随襟翼摆角位置的变化.由图4(a)可以看出，在3种攻角下，襟翼位于负角度位置时，升力系数相对原始翼型(摆角为0°时)均有增大，并随着襟翼摆角的增大而增大，最大增幅达到0.265；襟翼位于正角度位置时，情况反之，最大减幅约为0.287.攻角为0°和5°时，升力系数随襟翼摆角的变化关系比较相似，整体成线性发展，攻角为10°时，由于此时翼型尾缘已经发生绕流分离，襟翼位于负角度位置时，升力系数的增幅较为平缓.

(a)升力系数

(b)阻力系数

(c)升阻比

由图4(b)可以发现，襟翼位于负角度位置时，阻力系数相对原始翼型增大，并随襟翼摆角的增大而增大，增幅随着攻角的增大而趋于明显.襟翼位于正角度位置时，阻力系数在不同攻角下的变化情况略有不同：攻角为5°和10°时，阻力系数随襟翼摆角增大而减小，且攻角为10°时较为明显；攻角为0°时，阻力系数随襟翼摆角增大而略有增大.升阻比变化情况如图4(c)所示，攻角为0°时，襟翼摆角对翼型升阻比影响较大，随着攻角增大，升阻比受襟翼摆角的影响减小.

为进一步分析尾缘襟翼对翼型气动性能的影响机理，对上述3个攻角下襟翼摆角分别为-10°、0°和10° 3种情况下翼型表面压力系数进行对比，结果如图5所示.图5(a)中，襟翼摆角为-10°时，受襟翼影响，翼型整体吸力面压力系数较原始翼型减小，压力面压力系数较原始翼型增大，压力系数曲线所围面积增加是翼型升力系数增大的主要原因.襟翼摆角为10°时，情况与上述相反，由图4(a)可知，此时翼型升力系数为负值，结合图5(a)可以看出，此时翼型压力面与吸力面相对原始翼型已发生整体的相互转化.图5(b)和图5(c)的情况与图5(a)类似，均出现了相同规律的压力变化，且当襟翼位于负角度位置时在靠近尾缘位置出现了部分压力面和吸力面的相互转化，并随着攻角的增大，转化区域减小.由以上分析可知，襟翼的摆动位置对翼型各处表面压力均有较大的影响，甚至导致压力面和吸力面的相互转化，最终导致翼型升、阻力有较大的变化.

为了较直观地观察不同攻角下尾缘襟翼附近流场状态，分析尾缘襟翼对翼型流场特性的影响，图6给出了翼型在攻角为5°和10°时襟翼附近流场流线图，因攻角为0°时流线变化与攻角为5°时类似，在此不予给出.攻角为5°状态下，襟翼处于原始位置，与正角度位置均未发现分离现象，襟翼的主要作用是改变尾缘附近的流动方向；襟翼位于负角度位置时，尾缘上表面附近有轻微流体分离现象，由图4可知，此处流体分离对于襟翼对翼型气动性能的调控能力影响不明显.攻角为10°时，原始翼型尾缘上表面附近已经能够发现分离现象，并伴有较小漩涡；襟翼处于正角度位置时分离程度降低，但因襟翼向上弯曲导致尾缘上表面附近压力增大，使来流逆压梯度增大，进而导致尾缘上表面出现明显漩涡；襟翼位于负角度位置时可观察到尾缘上表面出现明显分离现象，并伴有漩涡发生，从图4可以看出，此处流体分离影响了襟翼对翼型气动性能的调控，使得襟翼位于负角度位置时翼型气动性能随襟翼摆角的变化较为平缓.

(a)α=0°

(b)α=5°

(c)α=10°

(a)α=5°，θ=0°

(b)α=5°，θ=10°

(c)α=5°，θ=-10°

(d)α=10°，θ=0°

(e)α=10°，θ=10°

(f)α=10°，θ=-10°

3.2动态气动性能

图7(b)显示的阻力系数的动态变化亦为一条封闭“O”形曲线，且随着折合频率的增大，“O”形曲线开头增大，相同襟翼摆角下，襟翼由正角度位置向负角度位置摆动时阻力系数大于襟翼向相反方向摆动时的阻力系数，动态阻力系数对襟翼摆角的响应为超前响应，与升力系数变化情况相反.“O”形曲线整体外形随着摆动频率的增大，相对于静态结果顺时针旋转，CD最大值增大，最小值减小，动态阻力系数CD整体变化幅度随摆动频率增大而增大.

(a)升力系数随襟翼摆角的变化

(b)阻力系数随襟翼摆角的变化

Fig.7Dynamic changes of aerodynamic characteristics along with the angle of flap for different oscillation cycles

图8给出了翼型在攻角为5°、襟翼摆角为0°时静止状态与襟翼折合频率k=0.027时表面压力系数的对比.由图8可以看出，襟翼处于上摆状态时，翼型上表面压力小于静止状态下，下表面压力大于静止状态下，差距主要体现在翼型前半段，后半段差距不明显.襟翼处于下摆状态时，情况与上述相反.综合以上分析可知，襟翼摆动迟滞现象导致翼型表面压力迟滞，这种迟滞主要体现在翼型前半段，表面压力迟滞使升力系数发生迟滞.

图9给出了翼型在攻角为5°、襟翼摆角为0°时静止状态与襟翼折合频率k=0.027时尾迹涡量图.由图9可以看出，襟翼运动的动态特性在尾迹涡量变化中亦有一定体现.襟翼处于静止状态时，翼型上表面的尾迹涡量略小于下表面.襟翼处于上摆状态时，翼型上表面的尾迹涡量较静止状态增大，下表面的尾迹涡量减小，致使升力系数增大.襟翼处于下摆状态时，情况与上摆状态相反，升力系数减小.尾迹涡量的大小在一定程度上反映了翼型升力的大小，襟翼运动时压力场与涡量场均存在一定的迟滞效应，体现在宏观参数上为升、阻力的迟滞回环.在襟翼实际应用中，尤其是襟翼快速动作时，动态效应不应忽视.

图8　α=5°时静止与摆动状态下表面压力系数的对比

(a)θ=0°， 静止

(b)θ=0° ，上摆

(c)θ=0° ，下摆

图9α=5°时静止与摆动状态下尾迹涡量图

Fig.9Vorticity magnitude in static and oscillating state forα=5°

4结论

(1)采用湍流模型RNGk-ε模型并采用壁面贴体运动结构化网格，对襟翼静止与摆动状态下的气动性能模拟均具有一定的精度，可较好地模拟翼型流场气动特性.

(2)襟翼摆角位置对翼型升、阻力系数有较大影响，主要基于翼型表面压力系数的变化，整体升阻比变化随攻角增大受襟翼影响减小.

(3)襟翼运动状态下，翼型升力系数滞后于襟翼摆角，阻力系数超前于襟翼摆角，气动性能随襟翼摆角变化的曲线近似为封闭“O”形曲线，并随着摆动周期的减小，曲线开口增大；升力系数曲线整体随摆动周期减小逆时针旋转，升力系数变化幅度减小，阻力系数曲线整体随摆动周期减小顺时针旋转，阻力系数变化幅度减小.

(4)尾缘襟翼的运动导致相同摆角位置翼型表面压力系数与静止状态下存在差别，且主要体现在翼型的前半段，此动态特性在翼型尾迹涡量发展中也有一定体现.

参考文献：

[1]Power-technology.com. The world's 10 biggest wind turbines [EB/OL]. [2014-01-02].http://www.power-technology.com/features/featurethe-worlds-bigge-st-wind-turbines-4154395/.

[2]VEERS P S,ASHWILL T D,SUTHERL H J,etal. Trends in the design, manufacture and evaluation of wind turbine blades [J]. Wind Energy, 2003，6(3)：245-259.

[3]BARLAS T K, van KUIK G A M. Review of state of the art in smart rotor control research for wind turbines [J].Progress in Aerospace Sciences, 2010, 46(1): 1-27.

[4]BERG D, WILSON D, RESOR B,etal. System ID modern control algorithms for active aerodynamic load control and impact on gearbox loading [C]//TORQUE 2010: The Science of Making Toruqe From Wind. Crete, Greece：European Wind Energy Association， 2010.

[5]BARLAS T K, van KUIK G A M. State of the art and prospectives of smart rotor control for wind turbines[J]. Journal of Physics Conference Series,2007,75(1)：DOI:10.1088/1742-6596/75/1/012080.

[6]TROLDBORG N. Computational study of the RisØ-B1-18 airfoil with a hinged flap providing variable trailing edge geometry [J].Wind Engineering, 2005, 29(2): 89-113.

[7]LACKNER M A, van KUIK G A M. A comparison of smart rotor for control approaches using tailing edge flaps and individual pitch control [J]. Wind Energy, 2010, 13(2/3):117-134.

[8]ANDERSEN P B. Advanced load alleviation for wind turbines using adaptive trailing edge flaps: sensoring and control [D]. Roskilde, Denmark: Technical University of Denmark, 2010.

[9]LACKNER M, van KUIK G A M. The performance of wind turbine smart rotor control approaches during extreme loads[J]. Journal of Solar Energy Engineering, 2010, 132(1):1-8.

[10]余畏，张明明，徐建中. 基于柔性尾缘襟翼的风电叶片气动载荷智能控制[J]. 工程热物理学报, 2013, 34(6):1055-1060.

YU Wei, ZHANG Mingming, XU Jianzhong. Effect of smart rotor control using deformable trailing edge flap on aerodynamic load reduction[J]. Journal of Engineering Thermophysics, 2013, 34(6):1055-1060.

[11]叶舟，赵海洋，高伟,等. 柔性翼型主动控制与气动特性分析[J]. 排灌机械工程学报, 2013, 31(10)：884-887.

YE Zhou, ZHAO Haiyang, GAO Wei,etal.Analysis on active control and aerodynamic characteristics of flexible airfoil[J]. Journal of Drainage and Irrigation Machinery Engineering, 2013, 31(10):884-887.

[12]李传峰，徐宇，赵晓路,等.风力机翼型尾缘襟翼动态特性分析[J]. 工程热物理学报, 2014, 35(5):883-887.

LI Chuanfeng, XU Yu, ZHAO Xiaolu,etal. Analysis on dynamic performance of trailing edge flap on wind turbine airfoil[J]. Journal of Engineering Thermophysics, 2014, 35(5):883-887.

[13]SOMERS D M. Design and experimental results for the S809 airfoil[R].Pennsylvania, USA: National Renewable Energy Laboratory, 1997.

[14]俞国华. 水平轴风力机叶片失速问题研究[D]. 上海：上海交通大学，2013.

[15]张鸣远，景思睿，李国君. 高等工程流体力学[M]. 7版.西安：西安交通大学出版社，2006.

[16]李鹏飞，徐敏义，王飞飞. 精通CFD工程仿真与案例实战[M]. 北京：人民邮电出版社，2011.

[17]高伟，李春，高月文，等.几何参数对风力机翼型转捩特性的影响[J]. 动力工程学报，2013，33(6): 490-496.

GAO Wei, LI Chun, GAO Yuewen,etal. Inflence of geometric parameters on transition characteristics of wind turbine airfoils[J]. Journal of Chinese Society of Power Engineering,2013, 33(6): 490-496.

Influence of Deformable Trailing Edge Flap on Aerodynamic Performance of the Wind Turbine Airfoil

HAOWenxing1,YEZhou1,2,DINGQinwei1,LIChun1,2

(1. School of Energy and Power Engineering, University of Shanghai for Science and Technology,Shanghai 200093, China; 2. Shanghai Key Laboratory of Multiphase Flow and Heat Transfer in Power Engineering, Shanghai 200093, China)

Abstract：Parametric programming was adopted on the modeling of deformable trailing edge flap (DTEF) to realize its flexible deformation and control, based on which numerical simulations were conducted to analyze the effects of DTEF on aerodynamic performance of the wind turbine airfoil and to study its flow mechanism respectively under static and dynamic conditions. Results show that under static conditions, the angle of flap affects the lift coefficient and drag coefficient obviously; with the rise of attack angle, the ability of DTEF reduces in changing the aerodynamic performance of the airfoil, and its influence on neighboring flow field weakens accordingly. Swing DTEF makes the change of lift coefficient of airfoil lags the change of flap angle, with reduced ability of DTEF on the control of lift coefficient; whereas swing DTEF makes the change of drag coefficient leads the change of flap angle, with enhanced ability of DTEF on the control of drag coefficient; these unsteady effects of flap oscillation are enhanced with the decrease of the oscillation cycle, reflecting in the variation of surface pressure coefficient of airfoil and in the development of wake vortex.

Key words：wind turbine airfoil; aerodynamic performance; deformable trailing edge flap; CFD

收稿日期：2015-07-15

修订日期：2015-08-26

基金项目：国家自然科学基金资助项目(E51176129)；上海市教育委员会科研创新基金资助项目(13YZ066)；上海市研究生创新基金资助项目(JWCXSL1402)

作者简介：郝文星(1991-)，男，河南商丘人，硕士研究生，主要从事风力发电方面的研究.

文章编号：1674-7607(2016)06-0473-07中图分类号：TK83

文献标志码：A学科分类号：470.30

叶舟(通信作者)，男，副教授，博士，电话(Tel.)：13917515193；E-mail：wstar_usst@163.com.