感悟数形结合思想，强化思维策略

花修平

摘 要：随着素质教育的不断发展和教育体制的变革，教育行业不断进步。而数学具有综合性、复杂性和逻辑性的学科，影响着学生未来的扩散思维和逻辑思维能力的养成。在进行数学课程教学中，使用数形相结合的方式，有助于学生创新思维和观念的养成，有助于提升数学课堂教学的质量和效率。在新课程改革不断深入的背景下，人们对数学教学有了更高要求，因此，就要求教师在教学的过程中，要充分运用数形结合的思想，促进学生发展。本文就结合苏教版初中数学教材，探究数形结合思想的优势和运用方法。

关键词：数形结合；初中数学；思维；战略

随着教育体制和社会的进步，社会对人才的要求越来越高，使得教育模式也随之发生改变，由原有的应试教育改变成为素质教育。但是，在现阶段初中数学教学的过程中，要求学生不但要全面地掌握知识，还要能够将知识运用到实际生活中，所以，教师要改变原来的教学方法，融入数形思想，使学生对知识的理解和吸收更加深刻。通常情况下，数形结合教学模式，能够在阐述知识时更具直观性，它能够把抽象的教材知识点转化为图像和图形，从而使学生更准确、牢固地掌握知识。

一、“数形结合”概述

数形结合就是把抽象化、难以理解的数学语言转变成为更加直观的图形，便于学生掌握和理解。从本质上说，就是把代数问题转变为几何问题。数形结合方法是对数学学科进行研究的关键方法，它能够把抽象、复杂的代数和形象直观的几何结合起来，把形象直观和抽象思维结合起来，使抽象的数学问题更加生动化和主观化，把抽象的思维转变为形象思维，能够促进学生更好地掌握、理解数学问题。在初中数学阶段使用数形结合的思想，有利于学生培养抽象性思维和数学逻辑思维。在数学教学中可以通过四个方面来开展：一是形成合适的代数模型，主要针对函数模型、不等式和方程问题；二是形成合适的函数图像或是几何模型，主要针对解决函数和方程问题；三是解决和函数相关的几何综合、代数等问题；四是使用图像的形式把要解决的问题呈现出来。使用数形思想的关键点就在于要把握好形和数的关联点。如果能够有效地把点和形结合在一起，就可以使很多难题迎刃而解。另外，教师要让学生在学习的过程中，使用综合、概括、抽象、分析、观察和类比，主动使用数形结合观念。

二、数形结合的有效策略

1.以数化形方法

以数化形方法就是把代数问题中的条件及数量关系利用图形表现出来，借助“图形”的直观性来探究数量关系，由数化形，数形结合，从而拓宽思路转化思维方式，使难题变为易题，直观、简捷地找到解题途径，这种思维策略体现了数形结合的数学思想的运用。

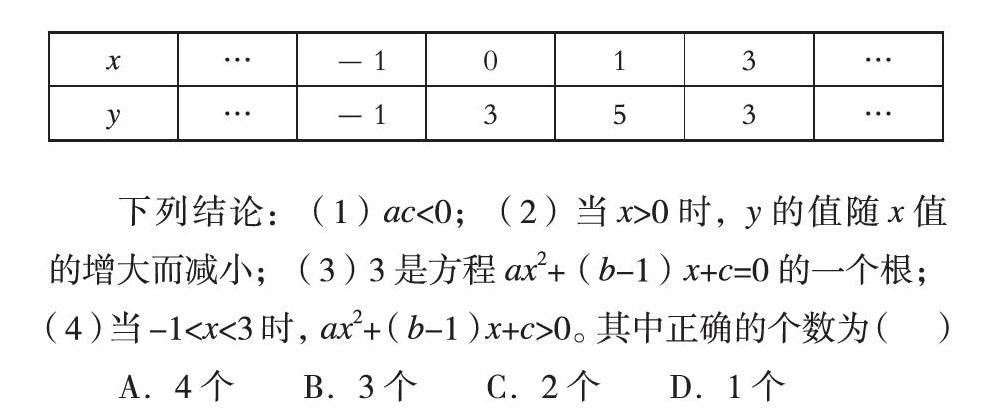
在数学教学中，这种思维策略要渗透给学生，在函数部分教学这一策略会经常用到。如下面这道题：二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如表：

下列结论：（1）ac<0；（2）当x>0时，y的值随x值的增大而减小；（3）3是方程ax2+（b-1）x+c=0的一个根；（4）当-10。其中正确的个数为（ ）

A.4个 B.3个 C.2个 D.1个

题目给出的数量关系是表格的形式，很多学生会根据数据求出二次函数的表达式后再去解决问题。实质上，从图表的数据中我们可以观察出，x从左向右在增大，而y的值先增大后减小，由此就可以确定抛物线开口方向是向下的，再根据对称性就可以画出抛物线的大致图像。利用图像解决问题能够降低这道题目的难度，从而将一个看似复杂的问题轻松解决，这样以数化形的策略把学生从问题困境中解救出来，也增强了学生学习数学的兴趣和信心。

2.以形变数

以形变数就是把几何问题中的变量用字母表示，用数量关系描述图形性质，从而将几何问题转化成代数问题。这种思维策略体现了数形结合思想和方程函数思想。

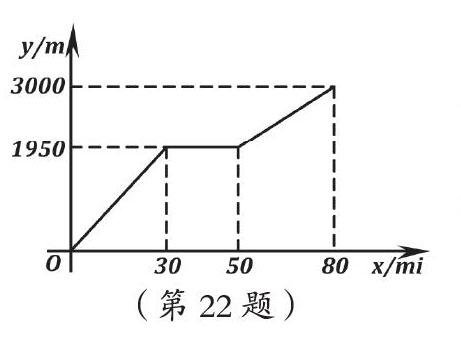
例如，某年南京中考数学的第22题，小颖和小亮上山游玩，小颖乘坐缆车，小亮步行，两人相约在山顶的缆车终点汇合。已知小亮行走到缆车终点的路程是缆车到山顶的路线长的2倍，小颖在小亮出发后50min才乘上缆车，缆车的平均速度为180m/min。设小亮出发xmin后行走的路程为ym。图中的折线表示小亮在整个行走的过程中y与x的函数关系。

小亮行走的总路程是多少，他途中休息了多长时间。

①当50≤x≤80时，求y与x的函数关系式。

②当小颖到达缆车终点时，小亮离缆车终点的路程是多少？

这是一道典型的数形结合题，题目中给了相应的图像和数量关系，并要求学生根据图像和数量关系进行分析，最后得出结论。根据题意我们可以得知，x、y分别代表一个变量，x代表的是小亮出发的时间，y代表的是小亮行走的路程，分析到这里，我们就可以直接得出第一小题的答案，从图形中直接就可以看出，小亮行走的路程是3600米，中途30～50分钟的时候，小亮的路程变化为0，由此得出，小亮的休息时间是20分钟。这道题解答到这里，我们已经可以从图像中得出这些内容，从而解答出第一题总路程为3600米，途中休息了20分钟。

再来看第二小问，根据题意我们可以知道，50～80分钟的时候，小亮行走的路程与时间之间的关系是一次函数的图像的一部分，因而把（50，1950）、（80、3600）两点的坐标代入一次函数的解析式，得出y与x的函数关系式，从而实现了以形变数的策略。

根据题中的文字描述我们可以知道，小亮行走的路程是小颖乘坐缆车行走的两倍，由此可以得出小颖乘坐缆车行走的路程为1800米，由于缆车的平均速度为180m/分，所以小颖乘坐缆车到达终点所用的时间是10分钟，由小颖在小亮出发后50分钟才坐上缆车，对应于图像，我们可以知道在小亮休息结束后，小颖又开始出发的，因而我们可以知道在小颖到达终点20分钟之后，小亮又到达了终点，也就是在小亮出发60分钟后，小颖就已经到达了终点。根据之前求出的x、y的函数表达式，可以将x=60带入，最后求出y的值，用3600减去y的值，就可以得出答案。这道题进行到这里我们可以看出，将图形转化成数的能力也是非常重要的，纵观几年来的中考题和模拟题，有许多的题目都是根据数形结合的思想，要么将数转化为形，要么将形转化成数，无论是哪种转化，都需要学生对数形结合的思想掌握地非常透彻。

三、数形结合的优势

使用数形结合，能够使学生解决疑难问题更具灵活性，使学生解决问题和分析问题的能力得以提升。在数学教学过程中，结合数形结合的思想，能够让学生更加理解数形结合是要找到形和数的关键点，再按照对象的属性，把形和数有效地结合在一起，互相转化，找到更为简单的解题思路。

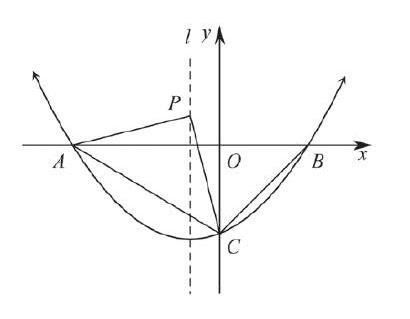
例如，2015年苏州中考数学试卷第27题：如图，已知二次函数y=x2+（1+m）x-m（其中0

本题主要考查了二次函数与几何的综合，以及勾股定理、相似三角形和二次函数最值求法等知识点。求P的坐标时，如果利用传统的方法，过P点作PD⊥y轴于点D，根据勾股定理构造方程可以得到P点坐标，不过这种方法的计算量很大。若采用数形结合的思想，由抛物线的对称性，得PB=PC，通过求BC的垂直平分线与抛物线对称轴l的交点即可。同样，在第3小题中需要证明∠ACP为直角，采用勾股定理的逆定理也是比较麻烦的。观察几何图形不难发现点A、B、C在⊙P上，因为∠ABC=450，所以很快得到∠ACP=2∠ABC=900。对于这样的中考压轴题难度是可想而知的，解题时必须在充分利用几何图形的性质及题设的基础上，挖掘几何图形中隐含的数量关系和位置关系，在复杂的“背景”下辨认、分解基本图形，或通过添加辅助线补全或构造基本图形，并善于联想所学知识，突破思维障碍，借助数形结合思想简化解题过程。

在教学过程中，教师要有意识地引导学生从不同角度去观察问题，就有可能得出不同的思考过程和不同的解题方法。因此，教师应注重学生数学思想意识的培养，逐步训练学生运用数学思想指导思维活动的能力，这样能够以量变促质变，从而优化解题过程，提高解题能力，并因此形成数学学习效果的广泛迁移，实现思维策略的强化。

参考文献：

[1]单淑娟.感悟数形结合归纳解题通法——“抛物线的变换”专题复习课的教学感悟[J].中学数学，2014（6）：25-26.

[2]焦剑.数学思想在教学中的感悟[J].东西南北·教育观察，2011（5）：107.

[3]陈花.“感受数形结合思想的内在力量”的实践与思考[J].教育界，2015（34）：122.

[4]竺忠燕.让学生在活动中感悟数形结合的思想方法——“面积与代数恒等式”教学案例[J].中国科教创新导刊，2011（12）：120-121.

[5]徐林超.让数学思想在课堂学习中获得感悟[J].中学课程辅导·教学研究，2012，6（13）：9.