采用终端滑模观测器的飞机防滑刹车系统执行机构故障重构

孙辉, 闫建国, 屈耀红, 张赞, 任杰

(1.西北工业大学 自动化学院, 陕西 西安　710129; 2.成都飞机工业集团, 四川 成都　610091)



采用终端滑模观测器的飞机防滑刹车系统执行机构故障重构

孙辉1, 闫建国1, 屈耀红1, 张赞1, 任杰2

(1.西北工业大学 自动化学院, 陕西 西安710129; 2.成都飞机工业集团, 四川 成都610091)

摘要：研究了基于终端滑模观测器的飞机防滑刹车系统执行结构故障重构的方法。针对常规滑模观测器渐进收敛而影响执行机构故障重构的时效性问题,利用终端滑模控制所具备的有限时间收敛特性,并且考虑实际系统故障信息未知的情况,构造非奇异终端滑模观测器(NTSMO)保证所有状态在有限时间内收敛于零,在等值控制方法的基础上给出了执行机构故障重构律。最后通过MATLAB仿真验证了所提方法的有效性。

关键词：飞机着陆;故障模式;故障诊断;无刷直流电机;李雅普诺夫方程;MATLAB

在近二十年来,反馈式的防滑刹车控制律有效应用于各类飞机防滑控制中[1-2]。然而,飞机防滑刹车系统数学模型却具有一定的非线性和不确定性。众多论文研究均是基于滑移速度控制式多门限偏压调节(PBM)的控制方法应用于防滑刹车控制律设计,但是由于防滑刹车系统常存在低速打滑现象,故而控制效果并不理想。现有的控制方式大多是基于最佳滑移率控制来设计相应的防滑刹车控制律[3-4],但这类设计均没有考虑刹车系统出现故障时处置策略。若刹车控制的执行机构一旦出现故障,不仅无法完成正常刹车,有时会使得飞机偏离跑道,造成不可避免的飞行事故。故障诊断作为飞机着陆研究的基础和关键技术,对保障飞机的安全运行具有重要的意义。

基于观测器的鲁棒型故障重构技术广泛被用于故障诊断领域中,常见的方法有基于传统滑模观测器、基于神经网络观测器、基于卡尔曼滤波估计器和基于自适应观测器的故障重构[5]。基于卡尔曼滤波估计器、神经网络观测器和基于自适应观测器的故障重构方法对参数的依赖性较强,容易受系统参数的变化影响。由于滑模观测器具有较强的鲁棒性,对系统的不确定性和非线性不敏感,可以达到故障重构的目的。文献[6]将滑模观测器应用于直流电机传感器故障的容错控制中,采用误差等效注入算法设计滑模观测器来重构传感器故障,取得了较好的控制效果。但在该文献中被控对象被简化为线性系统来进行考虑,其实效性较差,结论很难推广至非线性系统。文献[7]提出一种新型的滑模观测器设计方法,将传感器故障通过虚拟状态转换,等效为执行机构故障,重新设计二阶滑模观测器来检测和重构传感器故障。然而,该方法的应用并不能做到有限时间内的故障检测且未考虑外界扰动对故障重构的影响。文献[8]将高阶终端滑模观测器应用于非线性系统中的执行机构故障重构,但由于其引入一个线性变换矩阵实现系统降维,形成二阶系统,再通过构造终端滑模观测器来在线估计执行机构故障,而线性变换矩阵的构造较为复杂,并不具备一定的通用性。

传统滑模存在抖振,并且滑模观测器仅能保证系统可测量状态的有限时间收敛,而对于不可测量状态为渐进收敛性。对于全电刹车中的防滑控制盒来说,执行机构故障时飞机速度、机轮速度和刹车力矩均为可测量量,但执行机构(无刷直流电机)的转速,电枢电流为不可测量量。在采用传统滑模观测器进行状态估计是仅有飞机速度和机轮速度估计误差为有限时间内收敛,从而无法及时重构出控制执行机构输入的电压故障,即存在实时性较差问题。非奇异终端滑模观测器能够使系统状态在有限时间内收敛,有助于提高观测的收敛速度和重构精度,有关将滑模观测器同终端滑模观测器相结合的方法应用至故障诊断和故障重构领域鲜有报道。

综合以上考虑,本文针对实际系统存在执行机构故障上界未知及干扰等情况,提出一种基于非奇异终端滑模观测器的飞机防滑刹车系统输入控制电压故障重构方法,该方法结合传统滑模观测器及非奇异终端滑模观测器的优点,保证系统状态估计误差在有限时间内收敛,使得观测器具有全局稳定性,并利用误差等效注入方法对执行机构输入电压故障进行重构,通过对切换函数的优化,有效避免了常规滑模的抖振现象,最后,对本文所提出方法进行了数字仿真,验证了该方法的有效性。

1问题描述

考虑包含执行机构故障的刹车系统数学模型为不确定非线性系统,建立刹车系统模型时不考虑飞机的横侧向运动,假设所有主机轮的作动机构均具有一致性和同步性,因此刹车控制系统可以简化为仅对单个机轮的控制[9],而本文主要应用于基于滑移率设计的防滑刹车控制系统,则滑移率δ可以被定义为

(1)

对(1)式两边求导可得

(2)

式中

(3)

上述式中,Vx为飞机速度,ωw为机轮速度,Tb为刹车力矩,δ为滑移率,F1、F2和其他飞机机轮建模相关参数的定义详见文献[10],结合系数μ同滑移率δ之间具备非线性关系即

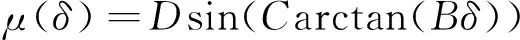
(4)

式中,μ-δ相关参数定义详见文献[11]。由于执行机构系统是由无刷直流电机构成,而电机是由电压输入来控制的,通过改变电压大小可以获得相应的刹车力矩,从而作用至刹车盘。故而将无刷直流电机当作系统的执行机构进行建模可得[12]

(5)

式中,TL=ηTb,η为输出力矩与负载力矩比值。无刷直流电机所有相关参数定义详见文献[12]。

综合(1)式至(5)式可得系统的非线性数学模型为

(6)

根据公式(6)所示,由(2)式、(4)式可知飞机刹车系统是一个较强的不确定非线性系统。

对于上述的刹车系统运动模型,为了分析简便,本文将其变换为状态空间方程的形式,考虑包含执行器故障的防滑刹车不确定非线性系统,定义:x1=δ,x2=Tb,x3=ωm,x4=im,u=U。(6)式可以写成如下形式

(7)

(8)

本文考虑的式执行机构故障,具体的无刷直流电机的输入控制电压发生故障,故障类型可以分为2种:①电压发生常值型缺失故障;②电压出现时变波动,即发生时变型偏移故障。

(9)

综上所述,本文研究的问题为:根据包含故障的防滑刹车非线性模型,(7)式,通过构造相应的终端滑模观测器使其所有状态估计误差在有限时间内快速收敛,并利用输入等效误差注入方法来完成执行机构输入电压故障的重构。

2滑模观测器设计

对于系统(7),同时考虑故障系数λ,可得

(10)

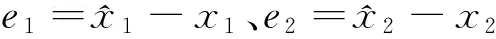
(11)

式中,sgn(·)为符号函数,L1、L2为正常数,且为观测器增益,v1=L1sgn(e1),v2=L2sgn(e2)。e1、e2为观测器估计系统可测状态量的误差。根据(10)式、(11)式,可将状态估计误差方程表示为

(12)

定理1对于非线性系统(10),同时满足假设1,从而设计观测器(11),选取较大的L1、L2能够保证自适应观测器渐进稳定。并且估计误差ei,(i=1,2)在有限时间内趋近于零。

证明选择Lyapunov函数为

(13)

对(13)式两端求导,由(12)式可得

g1e2-v1)+e2(g2e3-v2)

(14)

(15)

(16)

估计误差在有限时间内趋近于零,证毕

由定理1可知,可以用L2sgn(e2)/g2来估算e3。滑模控制通常选择一个线性的滑动平面,使系统到达滑动模态后,跟踪误差会渐进的收敛到零。但是仅调整参数并不会使得跟踪误差在有限时间内收敛到零。防滑刹车系统的刹车过程短暂,若执行机构发生故障,则重构故障的快速性,直接决定了系统进行容错控制的效果。终端滑模的应用能够使得滑模面上的跟踪误差在有限时间内收敛。考虑此优点,本文定义非线性滑模面为

(17)

设计相应滑模观测器如下所示

(18)

式中

v3=

(19)

式中,k0、k1、l、γ3、ξ均为正常数。

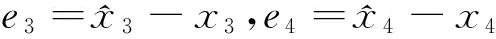
(20)

(21)

定理2考虑观测器误差(20)式、(21)式,同时构造非线性滑模观测器(18)式,若非线性滑模面s在有限时间内趋近于零,并且设计执行机构故障重构律为

(22)

且观测器增益取值为

(23)

满足选择常数γ4<ξ,λ取值足够大时,则状态估计误差e3、e4将在有限时间内收敛于零,执行器故障也将在有限时间内得到任意精度的重构。

证明该证明具体分为3步进行

Step1选择Lyapunov函数为

(24)

对(24)式两端求导可得

(25)

由于考虑(23)式,可知

(26)

由(26)式可知,非线性滑模面s将在有限时间t1内趋近于零

(27)

当滑模面收敛于零时,根据滑模面的定义(17)式可得

(28)

求解(28)式可以得出e3→0的时间t2,即

(29)

当e3在有限时间内收敛于零时,根据(20)式可得

(30)

根据滑模的等值原理,可以用(30)式来估算e4,则(21)式可重新写成

(31)

Step2根据(31)式,可以分析e4的有限时间收敛性,同样定义Lyapnuov函数

(32)

对(32)式,两边求导可得

(33)

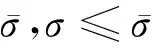
(34)

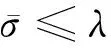
(35)

(36)

由上述可知,e4将在有限时间内t3收敛于零。

Step3由Step1、Step2可得出结论,当时间t≥t1+t2+t3时,其中t1≥ta、e1、e2、e3、e4均将趋近于零。将(32)式变化后两端同时求导,并且带入(34)式,可得

(37)

对(37)式进行变换可得

(38)

综上所述,当选择合适的观测器参数时,系统的状态估计误差e3、e4也将在有限时间内收敛于零,执行器故障也将在有限时间内得到任意精度的重构,至此定理2得证。

由于切换项的存在,滑模控制会产生抖振,为了减少抖振且消除抖动带来的高频干扰,本文选取双曲正切函数tanh(·)来代替符号函数sgn(·)

(39)

式中,τ为正常数。

通过上述分析可知,本文所设计的非奇异终端滑模观测器(11)、(18)可以确保系统状态估计误差ei,(i=1,2,3,4)在有限时间内,趋近于零,使得不可测状态量得到很好的估计,应用重构律(22)式,可以使得系统在有限时间内对防滑刹车执行器故障进行重构。

3仿真分析

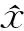
1) 故障类型1,当系统处于执行机构发生部分失效故障的状况,故障定义如下所示

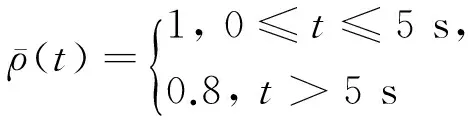
(40)

图1、图2中给出了本文所提出的观测器的状态估计情况,当系统正常时,从初始状态开始,观测器估计状态误差较小,一直保持在零附近,在5 s后发生执行机构常值部分失效故障,从图1、图2可以看出,状态估计误差均偏离滑模面,并能够及时侦测到执行机构故障的发生,但在有限时间内,状态估计误差均能够重新收敛于零附近。从图3、图4中可以看出,在0～5 s,由于执行机构无故障,因此故障重构值为零。在5 s后,执行机构出现故障,故障重构值能够快速逼近真实故障值,实现执行机构故障重构。

2) 故障类型2,当系统处于执行机构发生时变型偏移故障的状况,故障定义如下所示

(41)

3) 故障类型3,当系统处于执行机构即发生常值型部分失效故障,同时又发生时变型附加偏移故障的情况,即混合非线性故障,故障定义如下所示

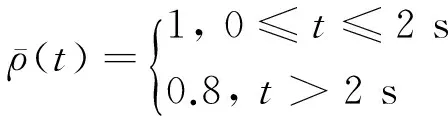
(42)

从图6可以看出,执行机构在2 s处发生部分失效故障,又过3 s后同时发生附加时变偏移型故障,本文所提出的重构律不仅能够对常值型部分失效故障重构,而且同时能够对附加时变偏移型故障进行准确重构,重构误差较小,并且有界。从重构效果来看,不论是故障处于刹车阶段初期时刻(t=2 s),还是故障期间的其他时刻(t=5 s),本文提出的算法均能够快速跟踪故障值,且重构精度较高。

在故障注入点,从图4可以看出执行机构重构值分别存在一个较大的估计误差量,这是由于在该时刻执行机构发生突变故障,继而导致滑模运动发生短暂破坏而引起的突变。但是在之后的时间内,执行器故障重构值相对于真实的故障均存在一定的重构偏差,这是由于等效注入是一种近似处理方法,对系统的故障重构是有一定影响的。但是考虑重构偏差较小,不会影响故障大小的总体诊断。故障重构结果表明,本文所提方法在全电刹车过程中对执行机构故障进行重构是有效的。

图1　滑移率实际值与观测值　　图2　刹车力矩实际值与观测值　　图3　执行机构故障实际值与重构值

图4　执行机构故障重构误差　　图5　重构执行机构时变偏移故障　　图6　重构执行机构非线性混合故障

4结论

本文针对飞机全电刹车系统执行机构故障重构问题,提出了一种基于终端滑模观测器的执行机构故障重构方法。该方法引入终端滑模的设计思想,设计相应的非奇异终端滑模观测器,通过滑模等值原理,进一步迭代,使得所构建的非奇异终端滑模观测器能够保证系统中所有的状态估计误差在有限时间内收敛于零。同时引入误差等效注入方法,对执行机构故障进行重构律设计,能够保证在有限时间内完成不同类型的执行机构故障的精确重构。

参考文献：

[1]Tseng H C, Chi C W. Aircraft Antilock Brake System with Neural Networks and Fuzzy Logic[J]. Journal of Guidance, Control, and Dynamics, 1995, 18(5): 1113-1118

[2]Mirzaei A, Moallem M, Mirzaeian B, et al. Design of an Optimal Fuzzy Controller for Antilock Braking Systems[C]∥Proc of the 2005 IEEE Vehicle Power and Propulsion Conf Chicago, USA, 2005: 823-828

[3]田广来, 谢利理, 岳开宪,等. 飞机防滑刹车系统的最佳滑移率式控制方法研究[J]. 航空学报, 2005, 26(4): 461-464

Tian Guanglai, Xie Lili, Yue Kaixian, et al. Study on Optimal Control Method of an Aircraft Anti-Skid Braking System Based on Slip-Ratio[J]. Acta Aeronautica et Astronautica Sinica, 2005, 26(4): 461-464 (in Chinese)

[4]李玉忍, 张智慧, 徐健龙. 飞机防滑刹车模糊滑模变结构控制研究[J]. 西北工业大学学报, 2015, 33(1): 45-49

Li Yuren, Zhang Zhihui, Xu Jianlong. Study on Fuzzy Sliding-Mode Variable Structure Control for Aircraft Anti-Skid Braking[J]. Journal of Northwestern Polytechnical University, 2015, 33(1): 45-49 (in Chinese)

[5]李娟, 周东华, 司小胜,等. 微小故障诊断方法综述[J]. 控制理论与应用, 2012, 29(12): 1517-1529

Li Juan, Zhou Donghua, Si Xiaosheng, et al. Review of Incipient Fault Diagnosis Methods[J]. Control Theory & Applications, 2012, 29(12): 1517-1529 (in Chinese)

[6]Edwards C, Tan C P. Sensor Fault Tolerant Control Using Sliding Mode Observers[J]. Control Engineering Practice, 2006, 14(8): 897-908

[7]Tan C P, Edwards C. Sliding Mode Observers for Detection and Reconstruction of Sensor Faults[J]. Automatica, 2002, 38(10): 1815-1821

[8]刘聪, 李颖晖, 刘勇智,等. 采用高阶终端滑模观测器的执行器未知故障重构[J]. 西安交通大学学报, 2015, 49(9): 126-133

Liu Cong, Li Yinghui, Liu Yongzhi, et al. Unkown Actuator Fault Reconstruction Based on the High Order Terminal Sliding Mode Observer[J]. Journal of Xi′an Jiaotong University, 2015, 49(9): 126-133 (in Chinese)

[9]王鹏, 李玉忍, 付龙飞,等. 基于扩展卡尔曼估计的飞机防滑刹车系统模糊控制[J]. 西北工业大学学报, 2015, 33(3): 478-483

Wang Peng, Li Yuren, Fu Longfei, et al. A Fuzzy Control of Aircraft Anti-Skid Braking System Using EKF(Extend Kalman Filter) Estimation[J]. Journal of Northwestern Polytechnical University, 2015, 33(3): 478-483 (in Chinese)

[10] 付龙飞, 田广来, 李玉忍,等. 反馈线性化飞机防滑刹车滑模变结构控制律研究[J]. 西北工业大学学报, 2013, 31(6): 962-966

Fu Longfei, Tian Guanglai, Li Yuren, et al. Designing an Effective Sliding Mode Variable Structure Control Law with Feedback Linearization of Aircraft Anti-Skid Braking System[J]. Journal of Northwestern Polytechnical University, 2015, 31(6): 962-966 (in Chinese)

[11] 王纪森. 非线性控制理论在防滑刹车系统中的应用研究[D]. 西安: 西北工业大学, 2001

Wang Jisen. Nonlinear Control Thoery and Its Application to Aircraft Antiskid Brake Systems[D]. Xi′an, Northwestern Polytechnical University, 2001 (in Chinese)

[12] Qiu Y, Liang X, Dai Z. Backstepping Dynamic Surface Control for an Anti-Skid Braking System[J]. Control Engineering Practice, 2015, 42: 140-152

收稿日期：2015-10-20

基金项目：国家自然科学基金(60974146、61473229)资助

作者简介：孙辉(1985—)，西北工业大学博士研究生，主要从事非线性系统故障诊断与容错控制的研究。

中图分类号：TP237

文献标志码：A

文章编号:1000-2758(2016)03-0386-07

Actuator Fault Reconstruction Based on Terminal Sliding Mode Observer for Aircraft Anti-Skid Braking System

Sun Hui1, Yan Jianguo1, Qu Yaohong1, Zhang Zan1, Ren Jie2

1． Department of Automatic Control，Northwestern Polytechnical University，Xi'an 710129，China2 Chengdu Aircraft Industrial ( Group) Co．，Ltd．，Chengdu 610091，China

Abstract:A method of fault reconstruction, which is based on terminal sliding mode observer, is proposed for aircraft anti-skid braking system. In the traditional sliding mode observer, the estimated error of unmeasured state is asymptotic convergence, which affects the timeliness of actuator fault reconstruction. In response to the above problem, the property of finite time convergence of terminal sliding mode is used to build a nonsingular terminal sliding mode observer (NTSMO), which ensures that all of the state estimation errors converge to zero in a finite time with the unknown actuator fault. Accordingly, a reconstruction law based on the specific equivalent control approach is then designed to accurately estimate the value of actuator fault in real-time and online. The performance of the proposed scheme is evaluated extensively through numerical simulations with MATLAB.

Keywords:aircraft landing, failure modes, fault detection, brushless DC motors, Lyapunov functions, MATLAB