基于浸入与不变的气动弹性系统反演滑模控制*

侯小燕 薛文涛 张 晨

江苏科技大学， 镇江 212003



基于浸入与不变的气动弹性系统反演滑模控制*

侯小燕 薛文涛 张 晨

江苏科技大学， 镇江 212003

针对外部扰动不确定的机翼气动弹性颤振问题，提出一种基于系统浸入与流形不变的自适应反演滑模控制方法。首先建立了带双控面和不确定外部扰动的气动弹性系统模型。然后结合反演和滑模控制理论设计了自适应Super-twisting反演滑模控制器，其中自适应扰动估计的设计采用浸入与不变方法，在系统整体自适应律中加入额外补偿项并建立扰动估计误差流形，通过自适应律的设计来保证误差流形的不变及吸引，从而保证扰动估计误差的收敛。最后对设计的控制系统进行了Lyapunov稳定性证明和仿真。结果表明，利用该方法设计的控制器外部扰动估计准确，翼段浮沉位移和俯仰角的控制优于传统的自适应滑模控制，气动弹性系统的稳定性和自适应性有所提高。 关键词 气动弹性机翼；浸入与不变；反演；自适应；Super-twisting；滑模控制

飞行器的气动弹性问题是气动力、弹性力和惯性力相互作用的结果，包括机翼颤振、操纵面嗡鸣及抖振等现象[1-3]。气动弹性系统的非线性也可能导致系统响应出现跳跃现象、极限环、模态交互和其它现象。颤振是一种复杂的非线性不稳定现象，包括极限环振荡、分岔和混沌运动等。颤振将严重影响飞行器的正常运行，导致结构疲劳甚至翼段损坏，由此可见，进行精确的非线性估计和相关的颤振主动抑制至关重要。

近年来，许多非线性气动弹性颤振的分析和控制技术取得了较大进展。例如,反馈线性化、极点配置、滑模和自适应方法等已尝试应用于机翼气动弹性系统的控制，并取得了一定的成果[4-7]。文献[8]采用反馈线性化策略对具有浮沉和俯仰角多项式的非线性二元机翼进行颤振抑制，并通过风洞实验验证了其有效性。文献[9]通过在线求解依赖于状态变量的Riccati方程来确定控制器，从而解决了非线性气动弹性模型的颤振问题。文献[10]设计了一种自适应模糊滑模解耦控制器，基于解耦系统的状态变量设计了2个滑模面，采用2个单独的输入实现浮沉位移和俯仰角的同步控制。然而这些方法对存在外部扰动的气动弹性系统自适应能力较差，仅能在一定程度上削弱外部扰动对系统的影响。文献[11]针对高音速颤振系统设计了一种自适应模糊滑模主动控制器，采用模糊方法来估计系统的非线性动态特性，并设计了自适应律和主动控制律来保证外部扰动下系统跟踪误差的快速收敛和其它信号的一致有界，该方法通过系统不确定估计提高了系统的鲁棒性，但系统的动态响应速度和参数估计精度有待进一步提高。

滑模控制具有较强的鲁棒性[12-13]，其滑动模态可以自由设计且与对象参数和扰动无关，但传统滑模由于控制量的不连续切换在实际应用中受限，这种不理想切换将导致系统抖振。反演法[14-15]不存在抖振现象，是一种严格收敛和基于Lyapunov函数的反步递推法，在增强系统的鲁棒性方面具有较大的灵活性。本文将两者结合进行气动弹性系统控制器的设计。

此外，自适应控制也常用于具有较多不确定因素和外部扰动的气动弹性系统。文献[16-17]提出了基于浸入与不变的自适应控制方法和参数估计方法，在系统参数估计律中引入额外补偿项来增加设计的自由度，对系统的未知参数进行估计，并使参数估计误差一致稳定收敛。浸入与不变通过保持流形的不变与吸引从而保证整个系统的稳定，将该思想应用于系统参数的估计上，相比传统的基于等价原则的自适应控制方法多出一额外补偿项，使系统参数的估计由原来的积分作用转化为比例积分作用，从而提高了参数估计的灵活性，改善了非线性自适应系统的控制性能。

针对带有不确定外部扰动的非线性气动弹性系统，本文将浸入与不变和滑模控制相结合，提出一种基于浸入与不变的自适应反演滑模控制方法。利用浸入与不变方法进行未知扰动估计来削弱外部扰动对系统的影响，反演滑模则采用反步递推设计了Super-twisting滑模控制器，克服了未知扰动估计偏差，提高了系统的稳定性，最后对设计的控制系统进行了仿真分析。

1 气动弹性系统建模

机翼气动弹性系统结构[18]如图1所示，根据气动弹性系统理论，以前副翼偏转角γ、后副翼偏转角β为控制输入，翼段浮沉位移h、俯仰角α为系统输出，建立系统运动方程如式(1)所示。本文采用滑模主动控制，通过前后副翼偏转角γ和β来控制翼段浮沉位移和俯仰角平稳输出，从而实现弹性机翼的颤振抑制。

图1 机翼气动弹性系统结构

(1)

式中，b为机翼半弦长，mt为主翼和控制部分的总质量，mw为主翼的质量，Iα为机翼惯性矩，xα是质心到弹性轴的无量纲距离，ch和cα分别为浮沉位移和俯仰角阻尼系数，kh和kα(α)分别为浮沉位移和俯仰角的弹簧刚度系数，L和M分别为气动力和力矩。这里kα(α)用以下非线性多项式表示：

αkα(α)=k1α+k2α3

(2)

引入非定长气动力和力矩公式[18]：

ρU2bclβspβ+ρU2bclγspγ

(3)

(4)

本实验的模型在对称机翼机构条件下，cmα=0，适用于低频、亚音速飞行条件。

为了方便起见，取c1=ρU2bsp，c2=ρU2b2sp，将式(3)改写为如下形式：

c1clββ+c1clγγ

(5)

定义状态变量和系统输出：

y=[y1,y2]Τ=[x1,x2]Τ。

将式(3)代入式(1)，并改写为状态空间方程：

(6)

cαnon1=-mtk2,

c1mwxαbclα(1/2-a)b(1/U)-cαmt,

ch1=khmwxαb,

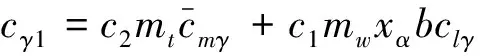
cαnon2=mwxαbk2,

c1Iαclα(1/2-a)b(1/U)+cαmwxαb,

ch2=-khIα,

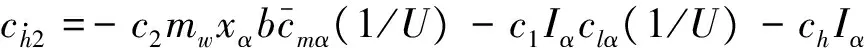
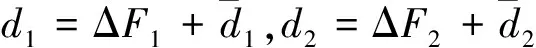
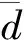
2 基于浸入与不变的自适应反演滑模控制

(7)

(8)

相比传统自适应控制，在自适应律中加入了额外补偿函数β1(x1,x3)和β2(x2,x4)，它的引入将使整体扰动估计由积分转换为比例积分，从而增加了扰动估计律设计的灵活性。整体自适应律不仅受扰动估计自适应率影响，也与额外补偿项β1(x1,x3),β2(x2,x4)有关。

设计Lyapunov函数：

(9)

(10)

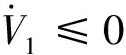
设计滑动面：

(11)

(12)

根据滑模理论设计包含Super-twisting项的二阶滑模控制器：

(13)

现在只需设计扰动估计自适应律w1,w2及额外补偿项β1(x1,x3),β2(x2,x4)，使流形保持不变和吸引。对扰动误差式(8)求导得：

(14)

选取扰动估计自适应律w1,w2如下：

(15)

将其代入扰动估计误差导数式(14)得：

(16)

对于式(16)，取Lyapunov函数：

(17)

(18)

取∂β1(x1,x3)/∂x3=γ1，∂β2(x2,x4)/∂x4=γ2，自适应增益γ1，γ2为常数。则β1(x1,x3)=γ1x3，β2(x2,x4)=γ2x4，至此基于I&I的自适应反演滑模控制律设计完毕。

下面分析系统的稳定性,整理式(12)和(16)得：

(19)

定义如下Lyapunov函数：

(20)

对于式(16)取Lyapunov函数：

(21)

其中，ks1,ks2,η1,η2,λ1,λ2,ε1,ε2均为正数。

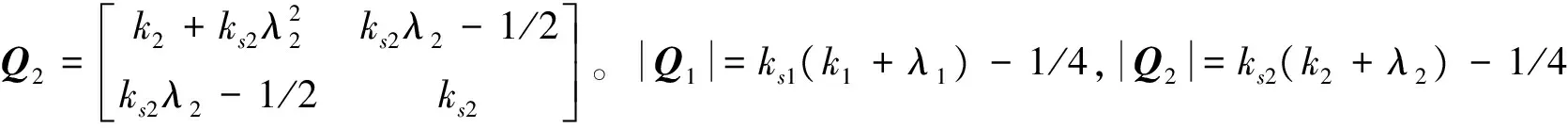
3 仿真分析

为验证所设计控制器的有效性，对给出的非线性系统(6)在控制器(13)作用下的响应进行仿真，并将结果与传统自适应反演滑模控制[19]在相同初始条件下的仿真结果进行比较。相较于文献[19]，本文的自适应控制器采用浸入与不变方法设计，在传统自适应律中加入了额外补偿函数，将整体扰动估计由积分转换为比例积分，提高了扰动估计的灵活性，且本文设计的控制器为Super-twisting二阶反演滑模控制器，与式(19)设计过程不同，Super-twisting控制项的引入同样可以简化控制器的设计，提高控制精度[20]。

系统方程中变量参数取值如下：

a=-0.6719,mt=15.57kg,mw=4.34kg,

ρ=1.225kg/m3,b=0.1905m,sp=0.5945m,

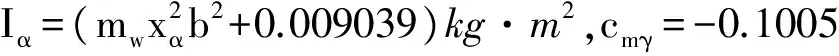
kα(α)=12.77+1003α2,xα=-(0.0998+a),

kh=2844.4N/m,ch=27.43kg/s,cα=0.036kg·m2/s,

clα=6.757,clβ=3.358,clγ=-0.1566,cmα=0,

cmβ=-0.6719。

图2为2种控制方法下气动弹性系统的仿真对比。其中，图(a)和(b)为浮沉位移和俯仰角的时间响应，图(c)和(d)为控制输入u1和u2，图(e)和(f)为滑动面s1和s2，图(g)和(h)为浮沉位移和俯仰角的相平面轨迹，图(m)和(n)为外部扰动估计d1和d2。

图2 两种控制方法的仿真对比

可以看出在给定输出参考轨迹情况下，尽管存在不确定外部扰动，由于扰动估计自适应律的引入，2种控制器均能稳定跟踪给定状态，实现气动弹性机翼颤振的主动抑制，但基于I&I的反演自适应二阶滑模控制对外部扰动估计更准确，且由于控制器中Super-twisting项的引入，加快了浮沉位移和俯仰角的收敛速度。由图(a)和(b)可以看出I&I ABSMC控制的机翼系统的浮沉位移和俯仰角过渡时间更短，收敛过程较平稳，消除了机翼系统的颤振和传统滑模的抖振。由图(c)～(f)可知在2种控制方法下，控制输入u1和u2和滑动面s1和s2最终都随系统的渐近稳定收敛至0，且收敛过程不存在抖振，但I&IABSMC控制下的控制输入和滑动面收敛速度更快。由图(g)和(h)可知，I&IABSMC控制下的浮沉位移和俯仰角相平面轨迹显然更平滑、稳定。图(m)和(n)表明基于I&I的扰动估计可以快速达到真实值，比传统的自适应估计更为准确。本文提出的I&IABSMC控制策略能有效控制机翼气动弹性系统运行在期望的状态，系统在存在未知外部扰动情况下仍具有较好的动静态性能。

4 结 论

针对外部扰动不确定气动弹性系统，将浸入与不变方法应用于不确定扰动的估计，并使用反演法设计了自适应Super-twisting滑模控制器。I&I在外部扰动估计时不遵循传统自适应控制的等价性原理，其稳定性由扰动估计误差的渐进收敛来保证。控制律的设计中，将反步递推和二阶滑模控制相结合，设计了包含Super-twisting控制项的连续二阶滑模控制器，保证了系统的稳定性和自适应性。仿真结果表明：基于I&I对扰动估计的准确性，翼段浮沉位移和俯仰角输出的稳定性得到提高。同时设计的连续滑模控制律也消除了滑模控制的抖振，加快了系统状态的收敛。

[1] 杨智春, 赵令诚. 飞行器气动弹性力学[M].西安: 西北工业大学出版社, 2009.(Yang Zhichun, Zhao Lingcheng. Aerodynamic elasticity mechanics[M]. Xi’an: Press of Northwestern Polytechnical University, July，2009.)

[2] Denegri C M, Cutchins M A. Evaluation of Classical Flutter Analysis for the Prediction of Limit Cycle Oscillations[C]. Proceedings of the AIAA Structures, Structural Dynamics, and Materials Conference, AIAA, Reston, VA, 1997: 1-10.

[3] Chen P C, Sarhaddi D, Liu D D. Limit Cycle Oscillation Studies of A Fighter with External Stores[C]. Proceedings of the AIAA Structures, Structural Dynamics, and Materials Conference, AIAA, Reston, VA, 1998:258-266.

[4] Ko J, Strganac T W, Kurdila A J. Adaptive Feedback Linearization for the Control of A Typical Wing Section with Structural Nonlinearity[J]. Nonlinear Dynamics, 1999, 18(3): 289-301.

[5] Yang C, Song C, Wu Z G, et al. Application of Output Feedback Sliding Mode Control to Active Flutter Suppression of Two-Dimensional Airfoil[J]. China Technological Sciences, 2010, 53(5): 1338-1348.

[6] Choi S B, Xu H, Mirmirani M D. LQG Control of a CFD-Based Aeroelastic Wing Model[C]. 42nd IEEE Conference on Decision and Control, IEEE Publisher, 2003, 5: 4939-4944.

[7] Huang R, Hu H, Zhao Y. Single-Input/Single-Output Adaptive Flutter Suppression of a Three-Dimensional Aeroelastic System[J]. Journal of Guidance, Control, and Dynamics, 2012, 35(2): 659-665.

[8] Strganac T W, Ko J, Thompson D E. Identification and Control of Limit Cycle Oscillations in Aeroelastic Systems[J]. Journal of Guidance, Control, and Dynamics, 2000, 23(6): 1127-1133.

[9] Singh S N, Yim W. State Feedback Control of an Aeroelastic System with Structural Nonlinearity[J]. Aerospace Science and Technology, 2003, 7(1): 23-31.

[10] Lin C M, Chin W L. Adaptive Decoupled Fuzzy Sliding-Mode Control of a Nonlinear Aeroelastic System[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(1): 206-209.

[11] Wang Y, Zhang Q, Zhu L. Active Control of Hypersonic Airfoil Flutter via Adaptive Fuzzy Sliding Mode Method[J]. Journal of Vibration and Control, 2015, 21(1): 134-141.

[12] Song C, Wu Z, Yang C. Active Flutter Suppression of A Two-Dimensional Airfoil Based on Sliding Mode Control Method[C]. 3rd International Symposium on Systems and Control in Aeronautics and Astronautics (ISSCAA), Harbin, 2010: 1146-1150.

[13] Chen C L, Chang C W, Yau H T. Design of Dynamic Sliding Mode Controller to Aeroelastic Systems[J]. Applied Mathematics & Information Sciences, 2012, 6(1): 89-98.

[14] Farrell J A, Polycarpou M, Sharma M, et al. Command Filtered Backstepping[J]. Automatic Control, IEEE Transactions on, 2009, 54(6): 1391-1395.

[15] Bouabdallah S, Siegwart R. Backstepping and Sliding- Mode Techniques Applied to An Indoor Micro Quadrotor [C]. Proceedings of the 2005 IEEE International Conference on Robotics and Automation, IEEE, 2005: 2247-2252.

[16] 刘振，谭湘敏，易建强, 等. 浸入与不变方法原理及其在非线性自适应控制中的应用[J]. 智能系统学报, 2013, 8(5): 400-407. (Liu Zhen, Tan Xiangmin, Yi Jianqiang, et al. Immersion and Invariance Theory and It’s Application in Nonlinear Adaptive Control [J]. CAAI Transactions on Intelligent Systems, 2013, 8(5): 400-407.

[17] Liu X, Ortega R, Su H, et al. Immersion and Invariance Adaptive Control of Nonlinearly Parameterized Nonlinear Systems[J]. IEEE Transactions on Automatic Control, 2010, 55(9): 2209-2214.

[18] Chen C L, Peng C C, Yau H T. High-order Sliding Mode Controller with Backstepping Design for Aeroelastic Systems[J]. Communications in Nonlinear Science and Numerical Simulation, 2012, 17(4): 1813-1823.

[19] Song Z, Li H. Second-Order Sliding Mode Control with Backstepping for Aeroelastic Systems Based on Finite-time Technique[J]. International Journal of Control, Automation and Systems, 2013, 11(2): 416-421.

[20] Shtessel Y, Edwards C, Fridman L, et al. Sliding Mode Control and Observation[M]. Birkhäuser, 2014.

Backstepping Sliding Mode Control of Aeroelastic System Based on Immersion and Invariance

Hou Xiaoyan, Xue Wentao, Zhang Chen

Jiangsu University of Science and Technology, Zhenjiang 212003, China

Inviewoftheaeroelasticflutterproblemofairfoilwithuncertainexternaldisturbances,amethodofadaptivebacksteppingslidingmodecontrol(SMC)basedonsystemimmersionandmanifoldinvariant(I&I)foraeroelasticitysystemisproposed.Firstly,themodelofaeroelasticsystemcontrolledbydoublecontrolsurfacesisestablishedwithuncertainexternaldisturbances.Thentheadaptivesuper-twistingbacksteppingslidingmodecontrollerisdesigned,whichisbasedonbacksteppingandslidingmodecontroltheories,theI&Imethodisusedtodesigntheadaptivedisturbanceestimation,andtheadditionalcompensationitemisinvolvedintothewholeadaptivelawandthedisturbanceestimationerrormanifoldisestablishedbyusingthedesignedadaptivelawtoensuretheinvariantandattractiveoferrormanifold.Therefore,theconvergenceofdisturbanceestimationerrorcanbeguaranteed.Finally,theLyapunovstabilityisprovedforthedesignedcontrolledsystem.Thesimulationresultsshowthatthedesignedcontrollercanaccuratelyestimatetheexternaldisturbanceandthecontroleffectofplungedisplacementandpitchangleissuperiortotheclas-

sicaladaptiveslidingmodecontrol.Thus,thestabilityandadaptivityofaeroelasticsystemareimproved.

Aeroelasticairfoil;Immersionandinvariant;Backstepping;Adaptive;Super-twisting;Slidingmodecontrol

*国家自然科学基金(61203024)

2015-05-11

侯小燕(1990-),女,晋中人,硕士研究生,主要研究方向为先进控制理论与应用等；薛文涛(1974-)，男，郑州人，博士，副教授，硕士生导师，主要研究方向为免疫算法、进化计算和智能控制等；张 晨(1989-)，男，南京人，硕士研究生,主要研究方向为先进控制与智能控制等。

TP316.2

A

1006-3242(2016)04-0003-07