基于双纽线轨迹的凸轮小车设计

徐　柳　彭松林　刘国凯　胡　南　余五新　马致远　廖志雄

(江汉大学 机电与建筑工程学院　湖北　武汉：430056)



基于双纽线轨迹的凸轮小车设计

徐柳彭松林*刘国凯胡南余五新马致远廖志雄

(江汉大学 机电与建筑工程学院湖北武汉：430056)

摘要设计了一辆将重力势能通过动力转换装置及转向机构来实现自动避障的‘8’字凸轮小车。小车采用伯努利双纽线作为主动轮的行驶轨迹，并推导刻画出凸轮以实现转向功能。利用MATLAB仿真工具模拟主动轮行驶的实际轨迹，并对小车关键参数进行单因素分析，总结变化规律，降低调试难度。进一步运过补偿分析，综合调节关键参数来降低因零件加工误差对轨迹的影响，合理地控制加工成本。

关键词无碳小车；凸轮机构；MATLAB；伯努利双纽线；误差分析

根据全国大学生工程训练能力大赛的命题要求，设计了一辆将重力势能通过动力转换装置及转向机构来实现自动避障的‘8’字凸轮小车。小车利用动力转换装置及转向机构来实现对不同间距障碍物的自动避障。‘8’字小车更是必须在较短距离内实现较大的转向，并在一定的加工误差及装配误差的条件下，尽量多地重复绕过障碍物。因此，小车结构设计的重点在于如何实现‘8’字轨迹并提高其重复度。

1结构设计

1.1总体结构及动力转换装置的设计

小车为了实现‘8’字避桩，必须连续性的完成转向过程，而小车在转弯时因存在差速问题，会造成行驶轨迹的突变，轨迹精度严重下降，甚至会导致翻车等状况。为了保证小车转弯时的平稳性，因而采用较慢速的单轮驱动，即将两轮中的一轮作为主动轮，起提供动力的作用，另一轮作为主要起支撑作用的从动轮。导向轮在转向机构的作用下实现小车的转弯。小车结构简图如图1。

图1　小车结构简图

小车动力转换装置利用定滑轮组系及绕线轮将重锤的重力转化为绕线杆的转矩，直接带动转向机构，同时经齿轮组将动力传递到主动轮，从而驱动小车在水平面内按‘8字’轨迹行驶。增设绕线轮是为了便于启动小车和控制小车低速平稳行使，故绕线轮的直径大小是保证小车匀速行驶的基础。

1.2转向机构的设计

转向机构[1]是由转向装置带动导向轮使其在任一时刻产生符合形成轨迹所需偏角的一组机构，其运动需具有周期性和连续性。采用凸轮机构[2]可很好地实现转向机构的运动要求。

伯努利双纽线的方程为[3]：

(x2+y2)2=2a2xy

(1)

2a=750mm时，其函数图像如图2所示，以该曲线为小车主动轮行驶轨迹，且此时2a为双纽线的横向总长。

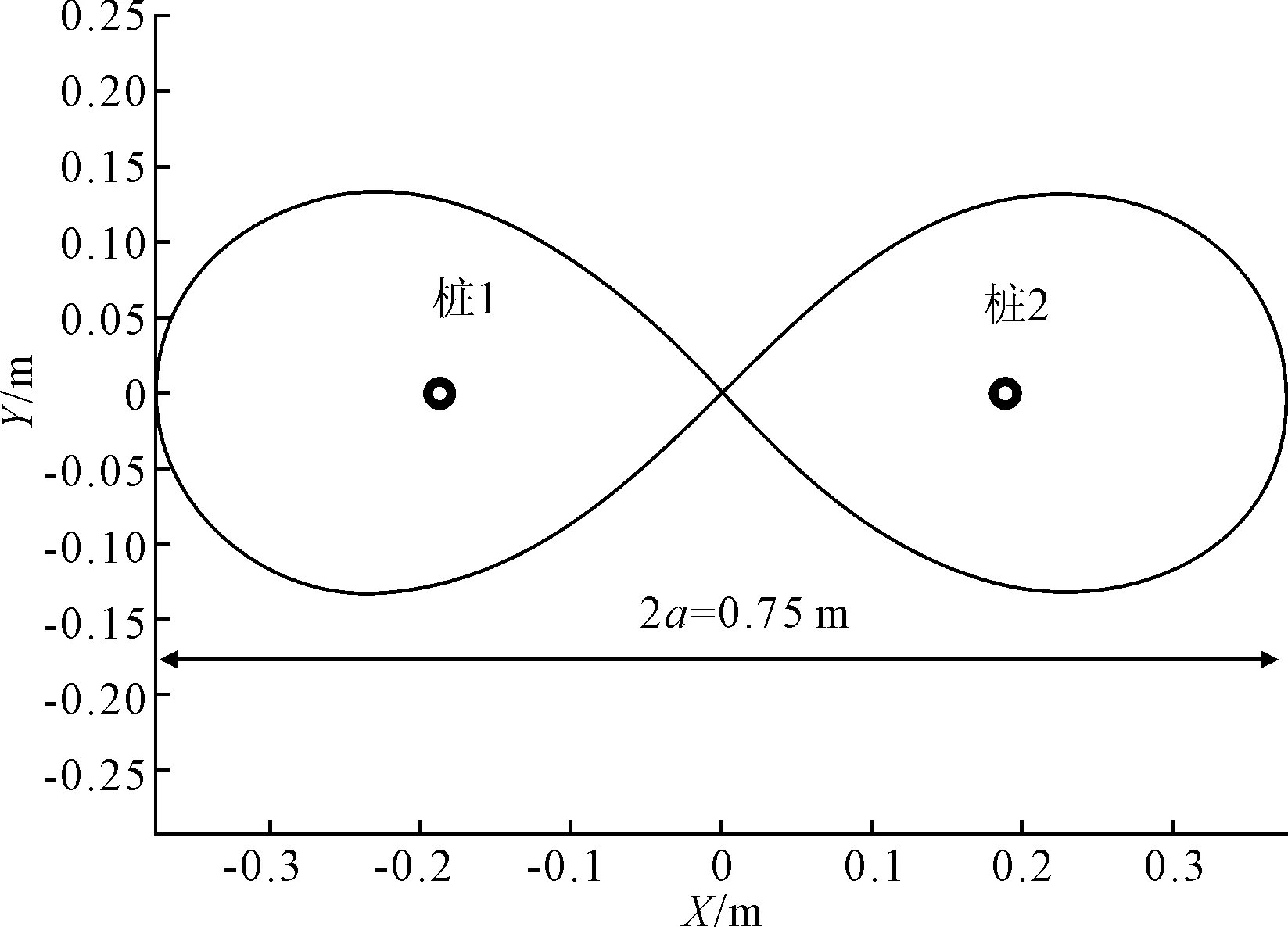
图2　伯努利双纽线

式(1)对应的参数方程为[4]：

(2)

主动轮轨迹的曲率为：

(3)

如图3，小车有左右转弯两种状态[5]，规定右转时θ为正值，则可将左右转弯的几何关系统一为式(4)，以便于后期仿真：

(4)

图3　小车转弯状态

由图1中小车结构简图可知，凸轮轮廓矢径A，转向机构中车身长D，推杆长L2，齿轮中心距C及凸轮距中心线横向距离L1在中心线上的投影满足几何关系：

(5)

联立(3)～(5)可得：

(6)

式(6)表明：小车主动轮轨迹点坐标与凸轮轮廓矢径一一对应，故用MATLAB[6]编程可将其刻画出来，具体轮廓如图4所示。

图4　凸轮轮廓

2实际轨迹生成

在转向机构中，凸轮作为实现转向功能的核心部件，又是保证转向精度的关键零件，因而校核凸轮轮廓的准确性尤为重要。可将凸轮轮廓任意一矢径反推出对应的主动轮与地面接触点坐标，运用MATLAB仿真[7]，即可生成主动轮行驶轨迹，亦即实际轨迹。

2.1前提假设

基于四点假设[8]：①小车运行过程中各轮在地面上纯滚动；②地面绝对平整；③小车运行过程中，零件的加工精度及整车的装配精度不会变化；④小车行驶时，不考虑空气阻力等影响，可用MATLAB仿真小车实际轨迹。

2.2实际轨迹推导

由图1及式(5)可知，小车导向轮转角满足：

(7)

双纽线的弧微分方程为：

(8)

小车在任意时间微元下，整车转角β与实际轨迹弧长ds的关系为：

(9)

则在该任意时间微元下，实际轨迹坐标增量为：

(10)

联立(7)～(10)可得任意时刻主动轮轨迹坐标为：

(11)

试选小车各参数及关键参数D，L1并结合式(11)应用MATLAB仿真得到若干个周期的主动轮行驶的双纽线实际轨迹如图5所示。

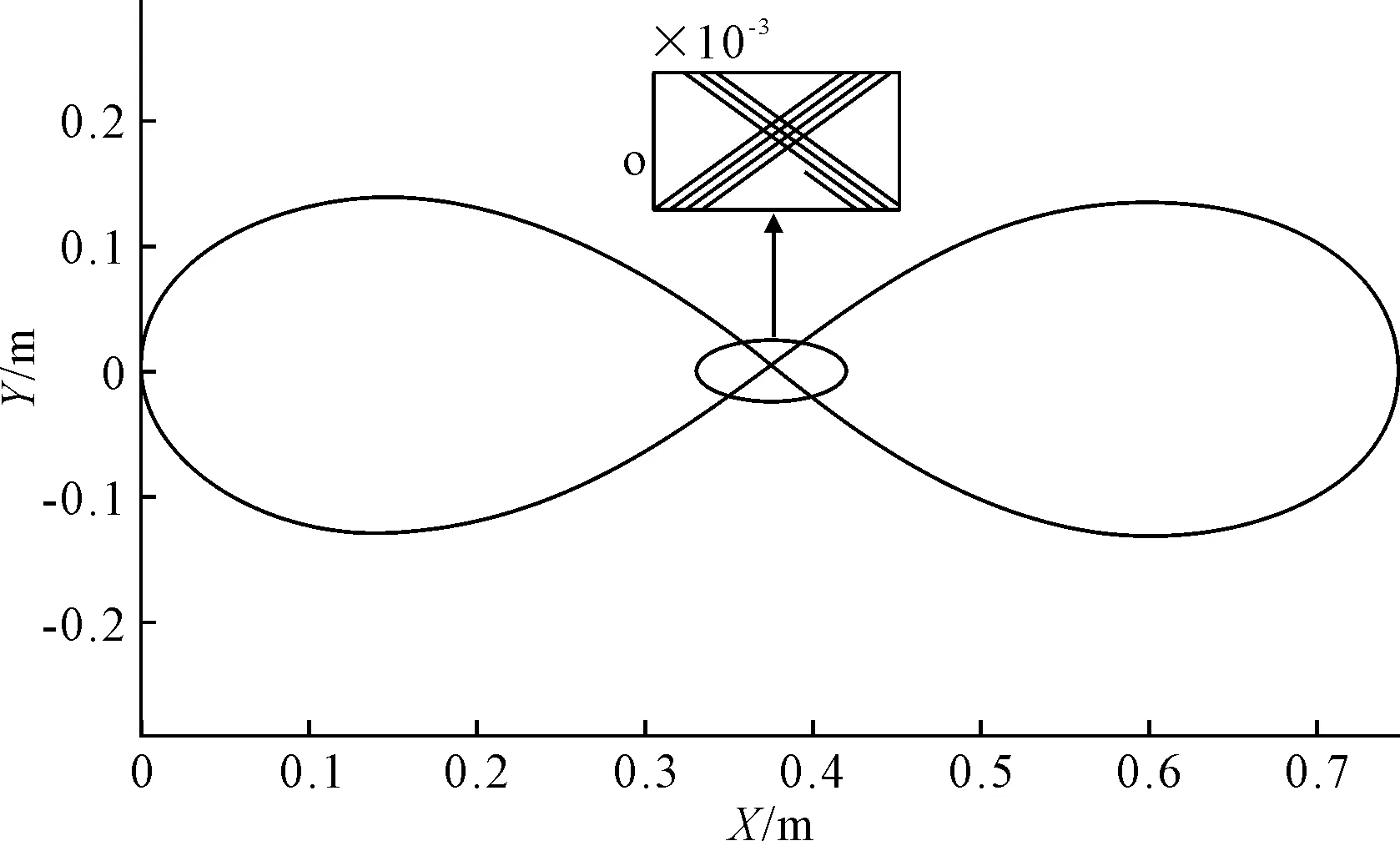
图5　小车实际轨迹

3关键参数单因素分析

在图5中，可以发现实际轨迹曲线并不封闭，在每一周期的起始及结束处有较小的偏差，这说明对于试选的参数D，L1不满足要求，需要通过对参数微调来完善仿真。

3.1D对实际轨迹的影响

运用控制变量法保持其他参数不变，等量调节D值大小，来探求D值的变化对实际轨迹的影响规律，其结果如图6(a)所示。由此可发现：D增大，实际轨迹明显发散，且绕对称轴逆时针偏转显著；D减小，实际轨迹亦明显发散，且绕对称轴顺时针偏转显著；不论D增大或是减小，实际轨迹左半部发散程度都远高于右半部。

3.2L1对实际轨迹的影响

同样运用控制变量法，保持其它参数不变，等量调节L1值，其结果如图6(b)所示。由此可发现：L1增大，实际轨迹略微发散，且绕对称轴顺时针轻微偏转；L1减小，实际轨迹亦略微发散，且绕对称轴逆时针轻微偏转；不论L1增大或是减小，实际轨迹左半部发散程度都略高于右半部。

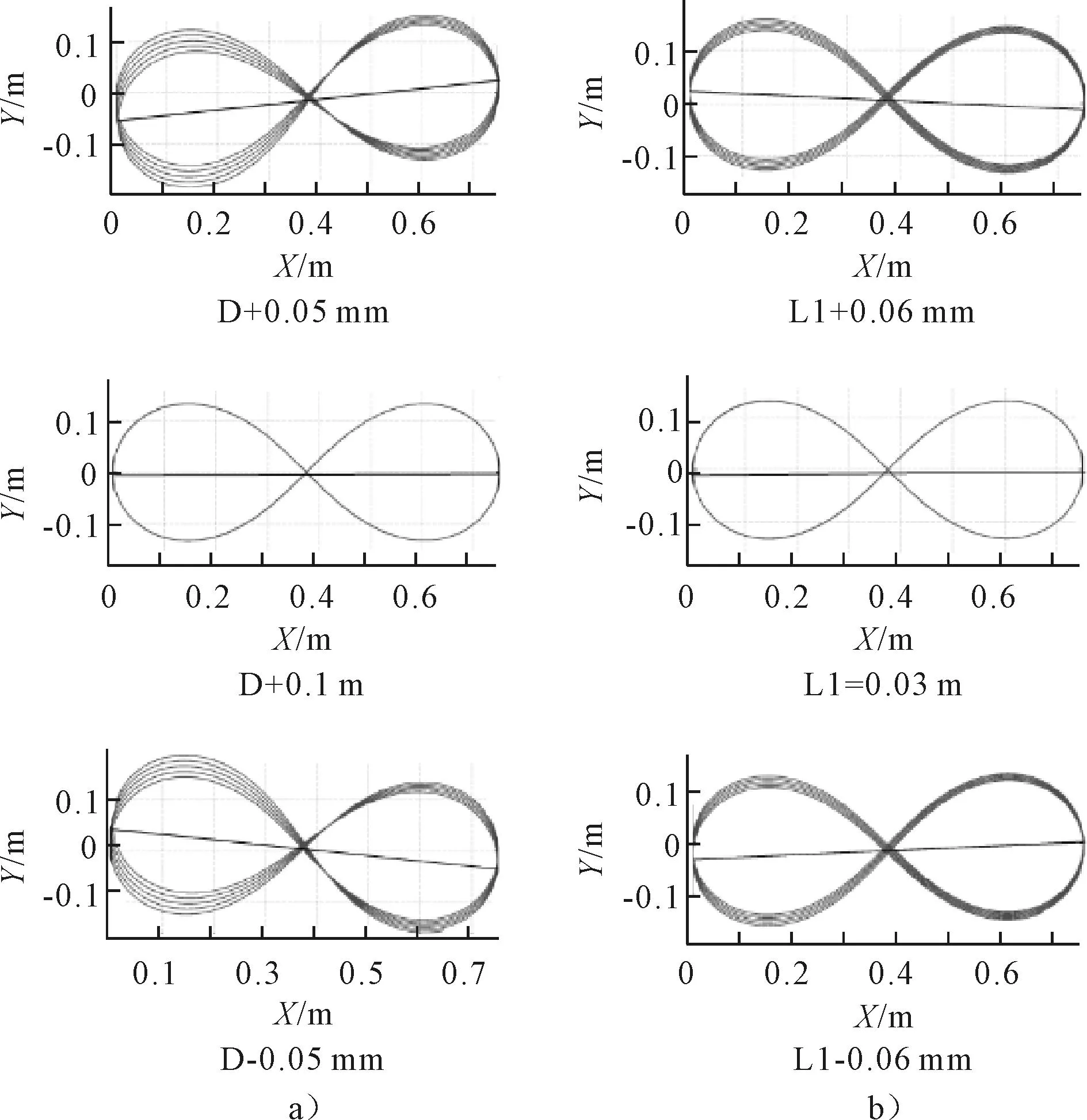
图6　D、L1单因素分析

综上所述，其他参数及凸轮轮廓都处在理想情况时，D和L1在寻常加工精度及装配精度条件下，综合调节此两者，可大幅提高实际轨迹精度与重复度。

4补偿分析

在转向机构中，凸轮作为核心零件，其误差敏感方向[9]是轮廓的法向方向，部分轮廓的加工误差直接反映到推杆上，对导向轮转角可能会造成严重偏差，影响轨迹精度。因此尝试通过分析凸轮加工精度对实际轨迹的影响，并利用综合调节D和L1来补偿其对实际轨迹带来的影响。

凸轮经济加工精度为IT11，表面粗糙度为Ra2.5～10。用MATLAB模拟凸轮实际轮廓矢径，使其误差在精度范围内随机变化，运用前述方法得到若干个周期实际轨迹如图7(a)所示。通过综合调节D和L1来修正实际轨迹如图7(b)所示。由图可知综合调节D和L1能对实际轨迹起到显著地补偿作用。

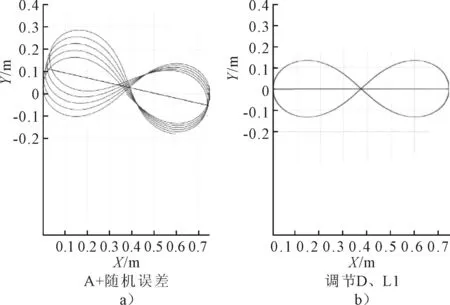
图7　凸轮补偿分析

5实验

为了尽可能地节省能量、减轻重量并保持车身的稳固性，小车多数零件采用铝合金制造。为了保障小车在通常加工精度及装配精度下能达到满意的效果，在推杆及转向杆处设计了微调机构以便D和L1可调。通过实验也验证了上述结论的正确性；仿真获得调节规律及误差可补偿范围，为后期小车快速调试到理想状态提供了有力保障。

6结论

通过数学建模并运用MATLAB，以伯努利双纽线为主动轮轨迹得到凸轮轮廓形状并对其正确性进行了仿真验证，发现实际轨迹每周期间存在微小偏差。进而深入研究了关键参数D和L1单因素对实际轨迹的影响规律，还进一步发现综合调节D和L1能对实际轨迹起到显著地补偿作用。也由此得出基于伯努利双纽线‘8’字凸轮无碳小车无需进行高精加工，只需增设D和L1微调结构即可满足要求的结论。

参考文献

[1]张玉航，黄力，王凯.8字绕障无碳小车转向系统的设计[J].科技创新导报,2014,(13):88-89.

[2]孙恒，陈作模，葛文杰.机械原理[M].北京：高等教育出版社，2006.

[3]同济大学数学系.高等数学[M].北京：高等教育出版社，2007.

[4]王叙贵.多卵线与双纽线——卡西尼卵形线与伯努利双纽线的推广[J].昆明师范高等专科学校学报，2001,23(4):34-36.

[5]方兴.智能车动力学模型参数辨识方法研究[D].上海：上海交通大学学报，2009.

[6]林雪松.MATLAB7.0应用集锦[M].北京：机械工业出版社，2005.

[7]卓金武.MATLAB在数学建模中的应用[M].北京：北京航空航天大学出版社，2011.

[8]曹斌，张海波，朱华炳.基于槽轮机构的8字小车轨迹无碳小车设计[J].合肥工业大学学报,2014,37(5):661-665.

[9]余承辉.机械制造基础[M].上海：上海科技出版社，2009.

(责任编辑：李文英)

Design of Cam Car Based on Lemniscate Trajectories

Xu LiuPeng SonglinLiu GuokaiHu NanYu WuxinMa ZhiyuanLiao Zhixiong

(School of Electromechanical and Architectural Engineering，Jianghan University， Wuhan 430056， Hubei)

Abstract:Our group designed a carbon-free car driving in 8-shaped track which achieved automatic aversion by the gravitational potential energy converting to the power and steering mechanism, using Bernoulli lemniscate as a driving wheel travel path, and deriving depicts cam to achieve steering function. Using MATLAB simulation tool to simulate actual trajectory of the capstan driving, the research makes use of single factor analysis to analyze key parameters of the car, to summarize variation and reduce debugging difficult. Further analysis by compensation, we made a comprehensive adjustment of key parameters to compensate for parts processing error caused by the impact of the track to analysis key parameters of the trolley single factor analysis, reasonably control processing costs.

Key words:carbon-free car; cam mechanism; MATLAB; Bernoulli lemniscates; error analysis

收稿日期：2016-04-15修回日期：2016-04-19

作者简介：徐柳(1994～).男，在读本科生*通讯作者：彭松林(1976～)，男，工学博士.E-mail：pslchb@126.com

中图分类号：TH112.2

文献标识码：A

文章编号：1671-3524(2016)02-0009-04