电学计量的误差分析及不确定度理论探究分析

刘佳+齐帮明+柴俭+张浩

摘 要：在电学检定和电学校准过程中，很多技术因素都会导致电学计量工作出现误差，同样在对不确定度进行分析计算时，由于计算失误也会导致误差产生。因此，针对这一情况，本文主要对我国电学计量过程中存在的误差进行分析及对其不确定度理论进行探究。

关键词：电学计量；误差分析；不确定度理论

【Abstract】In electrical and electrical test school registration process， many technical factors can cause electrical metrology errors， also in the analysis and calculation of the uncertainty due to miscalculation will lead to errors generated. Therefore， the response to this situation， this paper， the error of the electrical metering process exists to explore and analyze its theoretical uncertainty.

【Key words】electricity metering；error analysis； Uncertainty Theory

随着经济社会的不断发展，电学计量过程中所采用的测量硬件与软件都在不断升级，而且技术人员对测量结果的准确性也提出了更高的要求。因此，在电学计量过程中，及时发现测量系统中存在的误差和减小误差至关重要。电学计量工作由于其具有灵敏度高及准确度高等特点，因此在实际计量过程中会受到诸多不利因素的干扰和影响，从而导致测量结果出现误差。对此，物理学家海森伯结合量子力学理论提出了一种不确定关系理论，其在电学计量过程中广为使用。

1.电学计量的误差分析

一般而言，电学计量中存在的误差被称为确定性误差，这种系统误差是按照一定的变化规律出现的。因此，在电学计量中可通过误差恒值以及规律分布的误差，针对计量结果进行分析。在电学计量中，如果不能针对电学计量中存在的误差进行及时分析，则会对计量校准或检定结果产生严重影响。这种确定性误差与一般的电学计量偶然性误差不同，其很难被电学计量人员发现，而且很难利用数据发现误差、排除误差。所以，偶然性误差会对计量检定结果造成很大影响。确定性误差可以反映电学测量过程中的不确定度。在对测量不确定度进行评定时，技术人员只需结合数据测量结果就可对事物的优劣情况进行评定。所以，电学计量的精确度对电能计量产品的质量及国家经济效益的提升具有重要的意义。特别是在市场经济不断发展的时代，我国对外贸易经济也受到电学计量测量精度的影响[1]。因此，电学计量误差分析及不确定度理论探究，成为近年来相关领域学者高度重视的内容。

通过上述分析，本文发现系统误差主要分为人为误差及仪器误差和测量装置误差、环境误差、元件误差、电路等因素导致的误差；具体因素不同，误差形式也不同。其中人为因素误差主要分为操作误差及人员误差和温度等外界环境误差、计量读数误差等；仪器误差一般又分为间隔采样误差及标准量具误差和显示特性误差等；测量装置误差主要分为试验设备误差及灵敏度误差两种；具体到环境因素，其主要包括电流热效应及磁场因素和电路、电场稳定性等因素；至于元件因素主要包括稳定性因素及线性因素和非线性因素等；电路因素误差分为直角误差及交流电路中的相角和模等因素导致的误差。

2.电学计量的不确定度理论探究

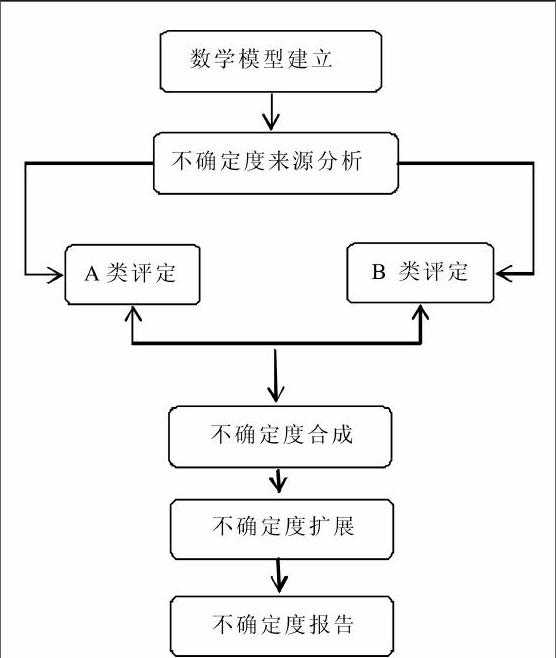
目前国内关于不确定度评定的理论研究主要分为动态测量不确定度评定方法以及静态不确定度评定方法两种。其中，对不确定度进行评定，首先需建立有关的数学模型，然后对不确定度的具体来源进行分析，最后针对不确定度进行科学评定，其中分为A类和B类两种，然后在此基础上对不确定度进行合成，与此同时需扩展不确定；除此之外，还需出具不确定度报告。如下流程所示：

电学计量的不确定度理论分析图解

结合上述图示，在实际应用过程中，首先需建立满足不确定度评定的数学模型，即通过电能计量中被测变量Y与影响量Xi，建立二者之间的函数关系式[2]：

按照上述公式，在测量过程中不能重复与遗漏数据，将所有电学计量过程中可能对不确定度造成影响的相关输入变量X代入上述数据模型中，从而根据实际情况建立新的数据模型。再通过输入变量X的值获得最佳参数值x，通过输入变量Y的值获得最佳参数值y，由此可得到新的数学关系式：

在上述计量模型中，xi的不确定度决定了被测量的不确定度。因此，对电学计量的不确定度分析，首先需针对x的不确定度进行评定。

在对不确度进行评定过程中，由于存在很多影响因素会导致电学计量结果准确性受到影响。因此，标准不确定度分量即是评定每个不确定度来源的标准偏差，通常可采用变量u来表示。而在合成不确定度时，可采用uc（y）表示电学计量中被测量估计值的标准不确定度，其主要由输入量的不确定度合成。而扩展不确定度通常可采用u来表示，即通过合成标准不确定度的倍数，表示电学计量不确定度，即将上述合成标准扩大k倍，从而获得测量的不确定度，最终得到如下计算公式：

在上述公式中，k通常为3或2，其主要由电学计量中被测量的效益、重要性及风险因素所决定。

最后，在出具不确定度报告时，测量不确定度采用合成标准不确定度U=kuc表示，因此需将自由度和uc已知；当采用扩展不确定度表示测量不确定度时，需将u c、p、v以及k已知，从而将更加详细的信息展示在不确定度报告中，提高测量结果的实用价值。

结束语

综上所述，通过对不确定度的评定理论研究发现，电学计量过程中测量不确定度的评定应用十分重要。由于电学计量结果在很大程度上与不确定度评定方式及理论存在很大关系。因此，在电学计量过程中，不仅需要提高测量硬件与软件的技术精准度，更要科学应用不确定度评定方法和理论，从而减小测量过程中的误差，防止受到不良因素影响，以此提高电学计量的科学性。

参考文献：

[1]肖婷婷.电学计量的误差分析及不确定度理论研究[J].科技信息，2013，16：480-481.

[2]王洋.探讨电学计量的误差分析及不确定度理论研究[J].科技与企业，2015，08：200.