柔性机械臂动力学建模理论与实验研究进展
谷勇霞 张玉玲 赵杰亮 阎绍泽
1.北京工商大学,北京,100048 2.清华大学摩擦学国家重点实验室,北京,100084
柔性机械臂动力学建模理论与实验研究进展
谷勇霞1张玉玲1赵杰亮2阎绍泽2
1.北京工商大学,北京,1000482.清华大学摩擦学国家重点实验室,北京,100084
摘要:总结了国内外学者在柔性机械臂建模理论及其相关实验等方面的最新研究进展,系统地阐述了柔性机械臂的变形描述方法、关节动力学建模、柔性机械臂系统的动力学建模方法、臂杆的刚化和软化效应、柔性机械臂实验方法等方面的研究现状,提出了现阶段机械臂动力学理论与实验研究存在的问题与不足,预测了柔性机械臂动力学研究的主要方向和核心技术,详细分析了柔性机械臂最佳模态阶数选取、基于动力学特性的柔性机械臂系统参数优化、关节驱动规律的确定、柔性机械臂在高速运转下刚化与软化效应、柔性机械臂关节精细建模、空间柔性机械臂超低速运行时爬行现象等待解决的关键技术问题。
关键词:柔性机械臂;动力学建模;刚度变化;实验研究
0引言
柔性机械臂因具有质量轻、能耗低、负载比高等优点而受到航空航天领域的广泛关注。但柔性机械臂由于臂杆和关节等具有柔性,故在运动过程中会产生弹性变形和机械振动,使机械臂的分析和控制难度增加,这严重制约了机械臂执行高精度任务的能力[1]。
关节一般包含电机、传动装置及传感器等,主要实现动力的产生与传递、位置感知和机械连接等功能,对机械臂的动力学性能、位置精度及运动平稳性起决定性作用,是整个柔性机械臂的核心[2]。相比臂杆柔性,关节传动装置的柔性是造成系统谐振的主要因素,对机械臂性能的影响更为显著,但研究者为了考虑臂杆柔性的影响,往往忽略了机械臂关节的动力学特性。另外机械臂在做大范围的空间运动时,臂杆变形与关节柔性相互耦合,导致机械臂在柔性变形中的振动频率与传统结构动力学中的振动频率不一致,即使在小变形条件下,机械臂的刚度也可能会发生显著变化,影响其动力学性能。因此,柔性机械臂的动力学行为表现为复杂的刚柔耦合现象,动力学方程呈现高度非线性、强耦合和时变性等特点,不易求解[3]。
本文结合柔性机械臂的特点,对柔性体的变形描述方法进行了概述,对柔性机械臂动力学建模的主要方法进行了分析对比,并介绍了机械臂关节动力学建模的研究现状。对机械臂刚化和软化效应机理进行了分析,总结了研究刚度变化问题的若干方法。最后对目前机械臂的实验研究现状进行了概述,并分析了影响机械臂动力学行为的关键技术问题,预测了今后机械臂动力学理论研究的方向。
1柔性机械臂建模理论研究
1.1柔性机械臂的变形描述方法
柔性机械臂的变形描述是柔性机械臂建模的前提,同时与动力学方程的求解难易程度密切相关。目前柔性机械臂的变形描述方法主要有有限元法、有限段法、假设模态法和集中质量法。王树新等[4]对上述变形描述方法进行了详细研究,认为采用有限元法所得到的动力学方程较为复杂、求解运算量大、计算效率低,相比之下,假设模态法具有系统性和效率高的特点。通过进一步调研发现[5]:有限元法对结构均匀杆件的计算效率和精度均较高,而对于复杂结构,动力学方程难以求解,不便于控制系统的建立。为得到含三个臂杆的柔性机械臂平面机构模型,Piras等[6]采用Lagrange方程与有限元法结合,将非线性方程转变为线性常微分方程以降低求解难度。而基于假设模态法对机械臂进行建模可以大大降低系统的自由度数和方程数,并且有利于后续控制系统的建立[7]。与有限元法相似,有限段法的求解效率较低,为了克服这一缺点,许多学者对提高有限段法的精度进行了研究。王树新等[8]采用有限段法建立了柔性机械臂的离散模型并在求解过程中引入相对位移的模态以提高计算效率。李文龙等[9]在采用有限段法对做大范围运动的柔性航天器进行建模时,提出将有限段法与空间算子代数理论结合的高效处理方法,有效解决了有限段法效率低的问题。集中质量法条理清晰,适用于构建形状比较复杂的柔性体,但采用集中质量法对机械臂建模时往往达不到精度要求[10]。因此,Ding等[11]将集中质量法和Holzer法相结合提出了Ding-Holzer法,有效提高了模型精度。
对于不同的结构可以选择不同的变形描述方法,目前仍以有限元法和假设模态法应用居多。
1.2柔性机械臂的动力学建模方法
对于柔性机械臂的建模,无论采用何种建模方式,都需要对柔性体的变形进行描述以及选取参考坐标等。目前主要有三类参考坐标系:惯性坐标系、随转坐标系和浮动坐标系[12]。
惯性坐标系根据大变形非线性有限元及连续体力学原理,将所有单元的运动都在惯性坐标系下描述,不再对各体刚体运动和弹性变形加以区分,适于大变形柔性建模。
随转坐标系是在柔性体的每个独立单元上建立参考坐标系,并随着每个独立单元的运动而运动,用于大位移、大转角和小应变结构的建模。
浮动坐标系(图1)由惯性坐标系X0OY0和柔性体上的随动坐标系X1OY1组成,将随动坐标系相对于惯性坐标系的大范围运动θ和相对于随动坐标系的弹性变形y(x,t)分开描述,浮动坐标系将多刚体动力学与结构动力学相结合,是目前应用最广泛的方法。Shabana[13]在对柔性多体系统动力学研究中详细阐述了浮动坐标系的选取问题。随着对大变形柔性体动力学问题的研究,出现了基于有限元与连续介质力学理论的绝对节点坐标法,该方法在全局坐标下定义单元的节点坐标,并将有限单元的节点转角坐标用斜率矢量代替[14]。
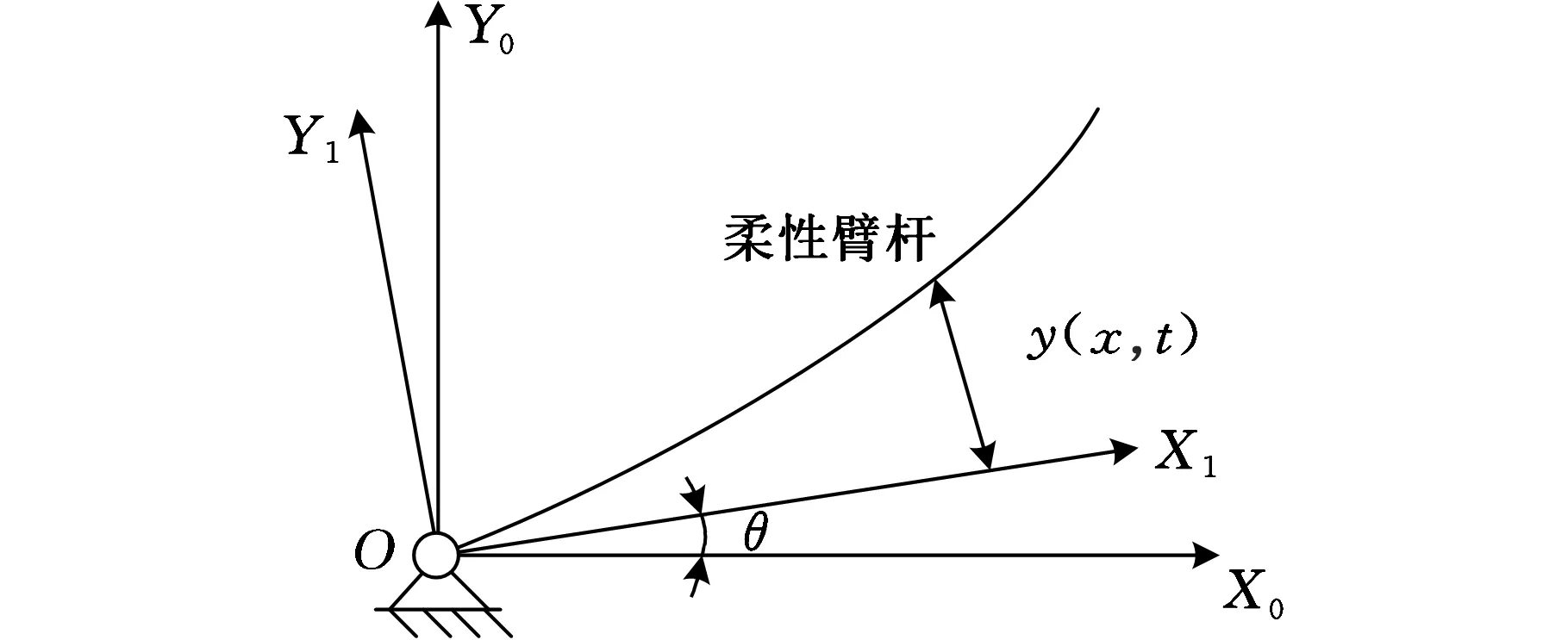
图1 浮动坐标系
随着柔性机械臂建模理论的不断成熟,建模方法也趋于多样化,但仍然以Newton-Euler方程为代表的矢量力学法和以Lagrange方程为代表的分析力学法为主。另外,还有兼具矢量力学法和分析力学法的Kane方程、基于极小值性质的高斯极值原理以及模型辨识法。王树新等[4]和杨敏等[15]对基于Newton-Euler方程、Lagrange方程及Kane方程的柔性机械臂建模方法进行了深入研究。在此基础上进一步调研发现:采用Newton-Euler方程建模时,由于难以消除方程中相邻物体间的内力项,对于复杂结构增加了建模的难度,求解效率降低。但Newton-Euler法是目前动力学分析用于实时控制的主要手段[16]。Lagrange方程形式简单,适合计算机高速求解,并可应用于控制系统。但建模过程中对动能和势能的推导以及微分运算复杂,广义坐标的选取也比较困难。目前Lagrange方程经常结合假设模态法被应用于柔性多体系统的动力学建模中[17]。采用Kane方程建模时不必考虑理想约束的约束反力,也无需进行系统的动能、势能及其偏导数的运算,且推导过程较为系统化,因此在多体系统的建模方面得到广泛应用[18]。上述柔性机械臂建模方法均需建立动力学方程进行动力学分析,而Gauss原理和模型辨识法可以不建立动力学方程就进行动力学分析,现分述如下:

(1)
根据高斯原理可知,质点系的真实运动满足
(2)
高斯原理在机器人的设计和分析中应用广泛,通过建立拘束函数的变分问题,可直接应用优化算法对机器人进行动力学分析[19]。
(2)模型辨识法。根据系统的实验数据来确定系统的数学模型,必须存在实际系统的输入输出数据。根据描述系统数学模型的不同,系统辨识一般可分为线性系统辨识、非线性系统辨识、集中参数系统辨识和分布参数系统辨识。各种方法的本质都是根据输入信号和响应信号辨识出系统的数学模型,如图2所示。基本流程都是根据辨识目的和先验知识设计相关实验,获取实验结果对模型参数进行估计,进而对模型进行验证,获得最终模型,其流程如图3所示。模型辨识方法在实验基础上获取系统的运动特征,抛开了经典力学分析的思想,从而为复杂柔性机械臂的动力学建模提供了有力手段[20]。

图2 系统辨识建模方法

图3 系统辨识流程图
虽然Gauss极值原理和模型辨识法可以避免动力学方程的建立,比较简单,但仍有许多关键技术问题尚需完善。目前对柔性机械臂的建模仍以Lagrange方程应用居多,其建模流程如图4所示。
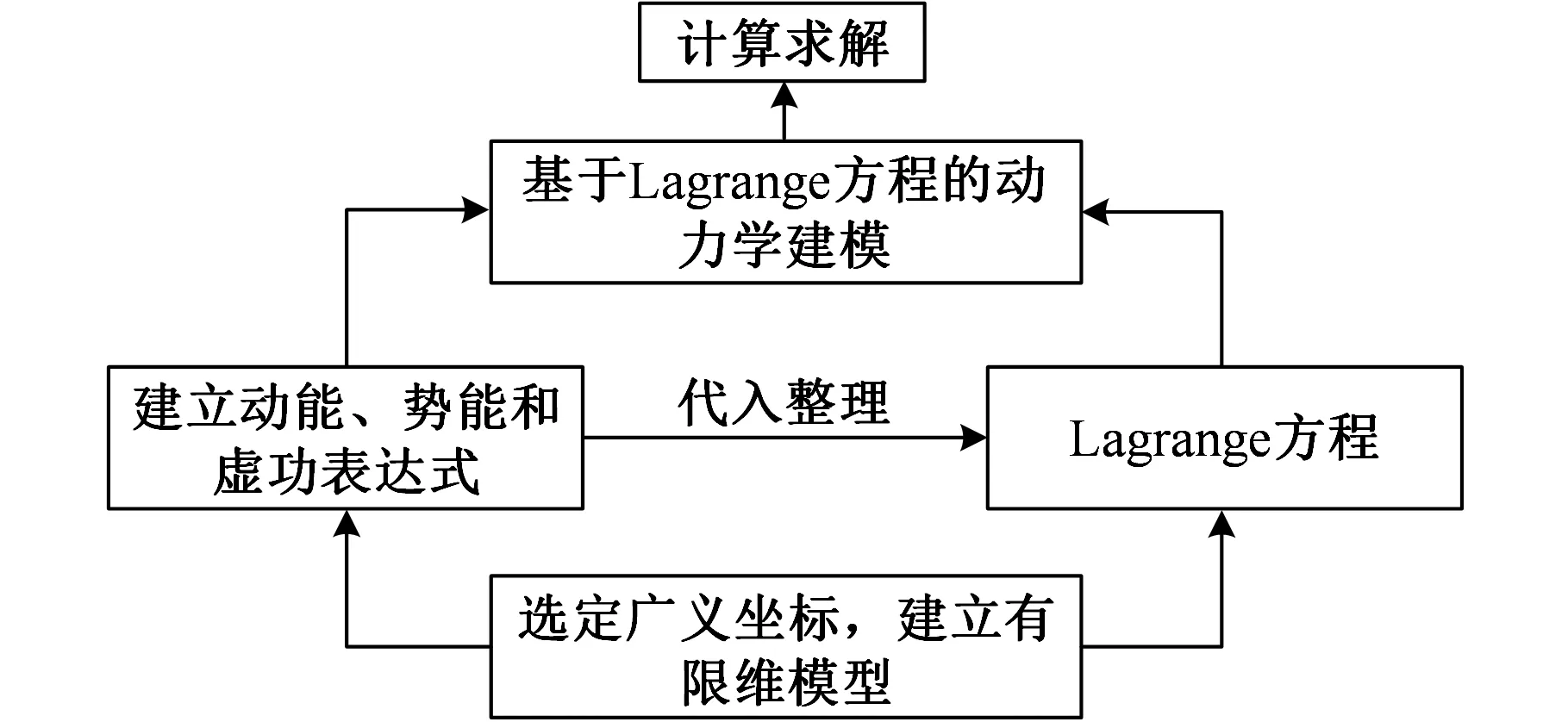
图4 Lagrange方程建模流程图
1.3柔性机械臂关节动力学建模方法
关节是柔性机械臂最关键的部件,其性能的好坏直接影响机械臂的工作性能,因此分析机械臂关节的动态特性对机械臂的控制至关重要,而建立精确的动力学模型是分析关节动态特性的前提。机械臂关节通常含有电机、行星齿轮或谐波齿轮减速器、位置传感器、旋转变压器及控制电路等[21],这些非线性部件会影响机械臂的动力学性能,导致机械臂关节模型的建立比较困难,需要同时考虑摩擦、阻尼、变形和间隙等因素。
早期的研究者往往忽略关节动力学特性的影响而重点考虑臂杆柔性,先后出现了铰链模型、线性扭转弹簧模型、弹簧-阻尼器模型等关节模型[22]。文献[23]将关节视为理想铰链,仅考虑臂杆柔性,建立了柔性机械臂的动力学模型并进行主动控制。之后Korayem等[24]考虑了关节柔性,分别将关节简化为线性扭转弹簧模型和弹簧-阻尼器模型来研究机械臂的建模问题。但这些简化模型都是基于刚性关节或关节小变形假设,不能体现关节的真实结构,对刚性较高的关节比较适用。实际关节在运动过程中会产生摩擦、阻尼、变形等影响机械臂动力学性能的非线性因素,上述简化模型忽略了这些非线性因素的影响,无法反映出关节的特性。在此基础上,许多学者对上述模型进行了修正。何柏岩等[25]在铰链模型的基础上考虑了铰链间隙,研究间隙对刚柔耦合机械臂动力学特性的影响。Erkaya[26]在非线性弹簧阻尼模型的基础上考虑间隙的影响,建立了关节的接触模型。
无论是理想关节模型,还是修正后的关节模型,由于未考虑摩擦等其他非线性因素,只适用于传动较为简单的关节,对于复杂传动关节往往不能满足精度要求,因此很多学者开始研究精细关节模型。于登云等[21]对细化关节模型进行了详细综述。在此基础上对机械臂关节的传动机构进一步调研发现:现有柔性空间机械臂关节一般采用行星齿轮传动或谐波齿轮传动作为减速机构[27],行星齿轮传动具有承载能力大、寿命长、可靠性高等优点,但在机械臂运行过程中,齿轮啮合会产生噪声和机械振动,影响机械臂动力学性能。研究表明,行星齿轮传动过程中时变啮合刚度、啮合误差和齿侧间隙是其主要问题[28]。Yang等[29-30]建立了考虑齿侧间隙、齿廓误差和时变啮合刚度的关节动力学模型并进行了仿真,仿真结果表明,齿侧间隙导致机械臂产生定位误差,而齿廓误差是影响加速度波动和啮合力的主要因素。杨天夫等[31]基于考虑间隙的滚动轴承模型和非线性啮合力的行星齿轮模型,建立了由四级行星齿轮减速器组成的大减速比精确机械臂关节模型。与行星齿轮传动不同,谐波齿轮具有传动比大、传动平稳等优点,由于采用弹性变形传递运动,故其关键问题在于摩擦和非线性刚度[32],这些关键问题会导致运行过程中产生动态误差、柔性和滞后等现象。谷勇霞等[33]建立了考虑谐波滞后的机械臂的动力学模型,并分析了谐波滞后对动力学特性的影响。Gomes[34]在刚体关节动力学模型的基础上,考虑了静态摩擦和库仑黏滞摩擦模型,并基于该模型设计了关节控制器,有效提高了模型动力学分析的精度。由此可知,随着建模理论的成熟,机械臂关节模型也不断得到完善。
2柔性机械臂的刚化和软化效应
柔性机械臂在运行过程中因机械臂柔性产生的变形与大范围的空间运动相互耦合,导致机械臂在其柔性变形中的振动频率与传统结构动力学中的振动频率不一致,即使小变形条件下,也会产生刚化效应[35];同时机械臂在运动过程中受到离心力作用,离心力导致机械臂变形,刚度减小,产生软化效应。两者相互作用使机械臂的刚度发生变化,因此刚度是衡量柔性机械臂性能的重要指标。传统的结构动力学理论分析中刚度通常为常值,不计小变形,但结构的大范围运动与小变形耦合以及本身变形导致的刚度变化,会对系统的动力学特性产生明显的影响。
2.1刚度变化产生的机理
刚度变化是刚化效应与软化效应相互作用的结果,以图5所示的柔性臂杆单元为例分析其刚度变化产生的机理。
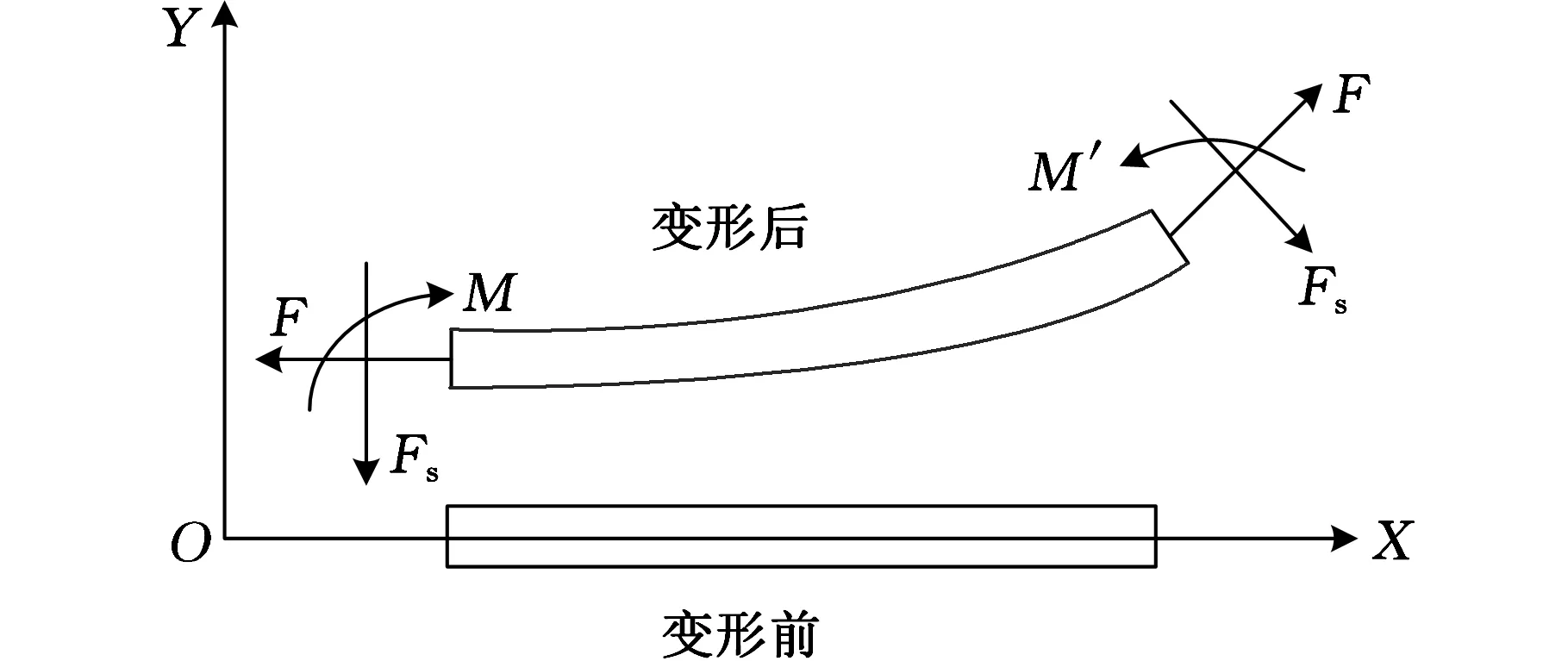
图5 柔性机械臂变形示意图
柔性机械臂在运行过程中产生柔性变形,对柔性臂杆单元进行受力分析,轴向力F提供了机械臂转动的离心力,弯矩M产生弯曲变形,不考虑剪力Fs的影响。变形前,F对M没有影响,但随着机械臂的旋转,其运动和变形的耦合会导致F产生附加的弯矩M′。附加弯矩计算公式为
(3)
由式(3)可知[36],当F很大时,附加弯矩不可忽略,并且随着转速的增大,轴向力不断增大,因此附加弯矩也随之增大,于是产生变化的附加刚度,即刚化效应,导致刚度增大,同时机械臂的柔性变形产生软化效应,使刚度减小,两者共同作用使刚度发生变化。
2.2刚度变化的分析方法
主要教学内容:针对某一具体装配对象进行系统研究,完成装配流程设计、视频采集、达宝易软件分析、标准作业指导书制订等,加强培养学生的实践应用能力。教学地点:实验室;教学课时:1周。
刚度变化与转速密切相关,目前在对机械臂建模时柔性体的变形描述一般采用假设模态法和有限元法,但这两种方法只适用于低速情况,对于高速情况,上述方法会导致仿真数值的发散[37]。
当前对刚化效应的分析方法主要有非线性有限元法、附加刚度法、变形耦合法及子结构法。非线性有限元法需采用隐式迭代算法,计算效率较低,早期主要用于简单柔性梁的动力学分析[38]。随着非线性有限元分析软件的成熟,该方法得到广泛应用,deBorst等[39]对其原理及应用进行了详细的总结。附加刚度法和耦合变形法是目前刚化效应分析的常用方法,但两者的应用也有很大的局限性。而几何非线性法是采用附加刚度法解决刚化问题的典型方法,它保留了位移与应变之间的非线性关系,所得刚度矩阵包含常值刚度阵和几何非线性刚度阵,一般表示为[38]
K=K0+Ks
(4)
式中,K0为常值模态的刚度阵;Ks为几何非线性刚度阵,即附加动刚度阵。
Sharf[40]认为该刚度阵是变形广义坐标α的无穷级数,因此式(4)的刚度矩阵K可采用Taylor展开近似表达为
(5)
其中,KG为α的线性函数,KB为α的二次函数,而且得到了KG和KB的显式表达式。许多学者对几何非线性法的精度给予了高度重视,如陆念力等[41]基于静力凝聚方法,建立了几何非线性刚度矩阵的递推公式,随着递推次数的增加,计算精度可以无限逼近精确解,但计算效率低。因此,需要进一步研究几何非线性法的精度问题。变形耦合法主要通过模态坐标的二阶小量来描述柔性体的变形场,形成精确到二阶小量的运动学描述以保留弹性变形的非线性特性。若取柔性体的前n阶模态,则变形场可表示为
(6)
其中,a为模态坐标,Nij为形函数,Nipj为耦合形函数。根据Lagrangian应变张量和小变形假设,可得耦合形函数为
(7)
再结合Kane方法,将偏线速度和偏角速度中的模态坐标进行线性化处理,由此可得柔性体的动刚度矩阵。阎绍泽等[42]基于变形耦合方法,在解决柔性体大范围运动产生的几何刚度方面作了深入研究。由于对于复杂形状的柔性体,难以得到耦合形函数,因此该方法只适用于简单形状的柔性体。子结构法与有限元法类似,但其子结构为线性变形,集合后的整体结构呈非线性。对于复杂结构,该方法计算量较大,效率较低,且要根据约束方程保证变形的连续性,在高速计算中准确性较好[43]。
虽然对刚化效应的分析趋于成熟,但却忽略了软化效应的影响。为了建立柔性机械臂的精细模型,研究者逐渐重视软化效应对柔性体的影响。吴胜宝等[44]对刚体-柔性梁系统的动力学特性进行了研究,结果表明柔性梁中同时存在刚化效应和软化效应,并影响梁的固有频率。由于刚化效应和软化效应结合使机械臂的刚度产生不确定的变化,影响机械臂的动力学特性,所以研究者提出了时变刚度模型[45],进一步细化了机械臂模型,但随着机械臂复杂化和高精度化,机械臂的时变刚度模型仍有待进一步研究。
3柔性机械臂实验的研究进展
3.1柔性机械臂臂杆实验研究
最早的机械臂实验系统为单连杆柔性机械臂,以DavidWang科研团队设计的实验系统(图6)为代表[46]。该实验系统的机械臂末端处于自由状态,并安装LED灯,与安装在基座处的CCD相机进行振动位移的测量[46]。臂杆采用直流电机驱动,电机的位置由安装在电机轮毂上的光电编码器完成。
斯坦福大学空间机器人实验室为了研究太空失重环境下自由漂浮物体的抓取过程,研发了宏/微机械臂,整套系统(图7)由两条长1.5m的宏机械臂和一组微机械臂组成,并通过空气轴承漂浮于花岗岩上[46]。

图6 David Wang科研团队的单连杆柔性机械臂[46]

图7 斯坦福大学的宏/微机械臂[46]
随着对多自由度机械臂的研究,双连杆机械臂的实验系统趋于成熟。余跃庆科研团队设计的两自由度机械臂实验系统(图8)以应变片作为传感器,PZT-5型压电陶瓷作为致动器,实现了模糊PID融合控制下的臂杆末端轨迹跟踪和柔性臂杆的残余振动控制[47]。

图8 余跃庆科研团队的双连杆柔性机械臂[47]
阎绍泽等[48]设计了双连杆机械臂主动控制实验平台(图9),该实验平台采用光电编码器、加速度计和应变片分别检测机械臂的大范围运动、末端振动位移和驱动力矩,实现了对机械臂结构-控制耦合特性的研究。另外,张令波等[49]提出了基于云模型的柔性机械臂关节轨迹跟踪和末端振动抑制的云控制器的设计方法,设计了一套基于位置敏感探测器(PSD)的双连杆柔性机械臂实验系统,并验证了控制器的实用性能,有效改善了测量精度。

图9 阎绍泽科研团队的双连杆柔性机械臂[48]
3.2柔性机械臂关节性能实验研究

图10 MSS关节实验系统结构图
国际空间站使用的移动服务系统(MSS)在空间站的服务中占据重要位置,可以完成精密装配、轨道装置之间的分离和对接以协助宇航员进行舱外活动等。加拿大航天局为了研究每个关节的性能,设计了测试MSS关节的实验系统,其结构如图10所示[50]。该实验系统主要用于测试关节输出力矩的相关特性、扭转刚度及弯曲刚度等性能参数,含有待测关节、在轨可更换单元、高刚度的适配器、行星齿轮增速器、制动器、加载用摆杆、紧急致停单元、传递力的弯曲箱、5个加载用的螺旋起重器,刚体结构台等。其中加载用摆杆通过在摆杆末端添加质量块来进行加载,关节轴向通过改变摆杆的长度和改变质量块的质量来调节关节的负载,关节径向通过螺旋起重器来改变负载。周留栓等[51]设计了基于虚拟仪器的模块化关节综合性能测试实验系统(图11),主要为了研究模块化关节的动静态参数及性能评定。该实验系统包括待测关节、圆光栅、扭矩传感器、磁粉制动器以及主结构支架等。
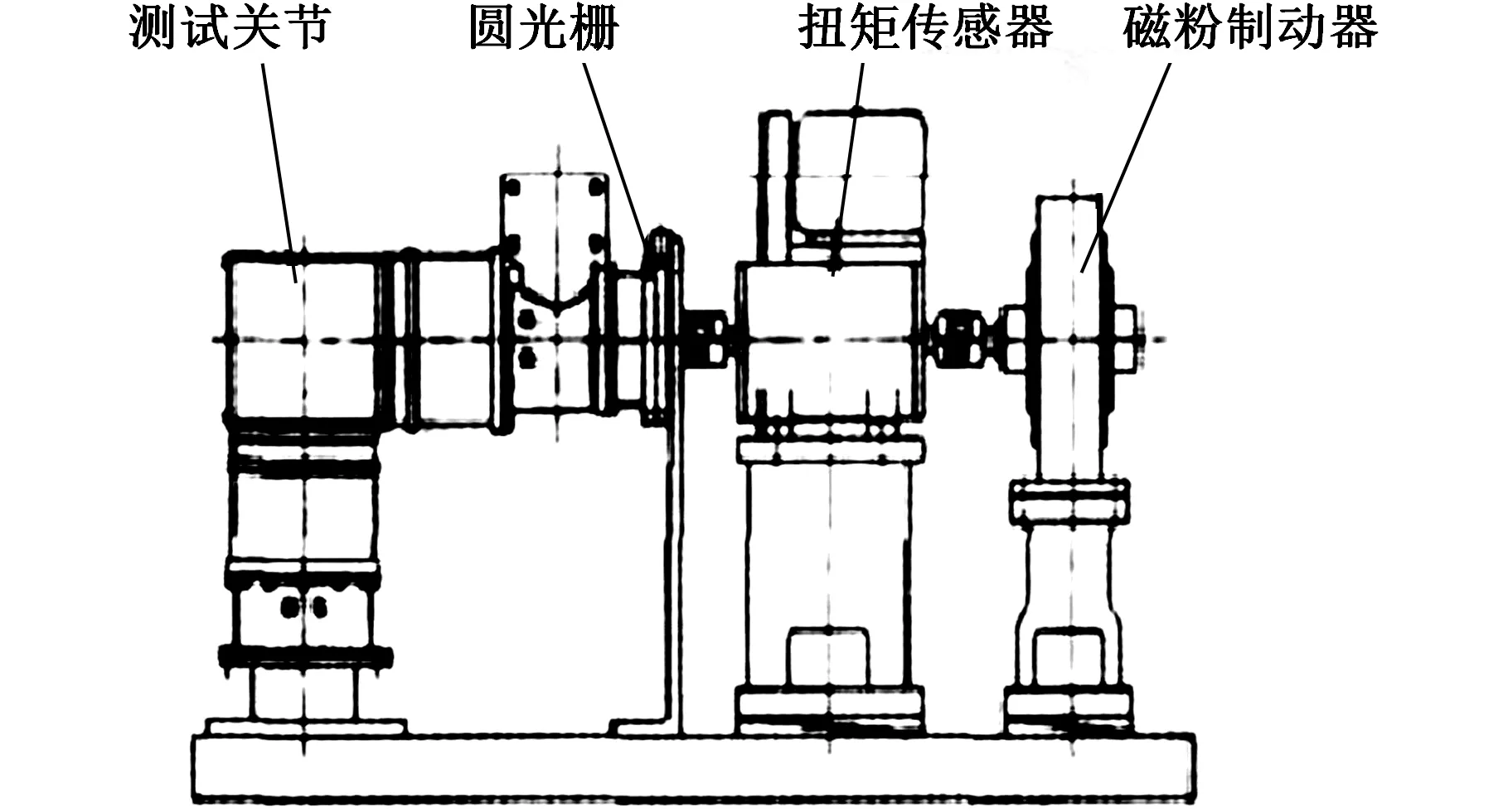
图11 模块化关节综合性能测试实验系统
北京邮电大学与合肥智能化研究所联合研制的空间机械臂原理样机如图12所示,其关节由直流无刷电机、谐波减速器、掉电制动器、旋转变压器等组成,结构紧凑、集成度高[52]。李成等[53]基于模块化设计思想,设计了具有行走和操作能力的空间机械臂(图13),并利用吊丝配重的方法抵消重力的影响来模拟太空环境。

图12 空间机械臂原理样机[52]

图13 机械臂关节[53]
4机械臂动力学研究若干关键技术问题
通过调研国内外学者对柔性机械臂动力学的相关研究发现,柔性机械臂动力学研究主要存在以下一些关键技术问题。
(1)柔性机械臂最佳模态阶数选取。柔性机械臂的动力学模型是连续无限维的,需要采用离散化方法对其变形进行描述,而求解结果的精度取决于模态阶数的选择,一般阶数越多结果越精确,但运算量也较大,而且实际也不必要。因此,如何选取模态阶数对柔性机械臂的动力学建模与分析至关重要。Skelton等[54]提出了基于分量价值分析的模态价值分析准则,其思想是根据各阶模态的模态价值对系统价值函数的贡献来决定对模态的取舍,保留那些对系统价值贡献较高的模态。模态价值分析准则直接将模态选择与控制目标联系起来,因而得到广泛的应用。目前也有学者研究基于实验研究的结构模态阶数选取。唐国潮等[55]等分别截取柔性机械臂的前四阶模态进行仿真,结果表明截取前三阶模态即可满足精度要求。一般针对不同的模型需要截取不同的阶数,如何选取最佳模态阶数值得深入研究。
(2)基于动力学特性的柔性机械臂系统参数优化。虽然机械臂臂杆和关节柔性等对机械臂动力学性能的影响占主要地位,但机械臂系统参数,如结构参数、物理参数、阻尼参数、关节转动惯量、末端附加质量的大小及位置对机械臂动力学性能的影响也至关重要。通过改变机械臂的结构参数(如截面宽度、高度、长度)和物理参数(如密度、弹性模量),研究其对机械臂动力学输出特性的影响,进而选择对动力学特性影响较小的臂杆截面和材料,可以为机械臂的振动抑制提供方法。郭振峰等[56]改变柔性机械臂的结构参数和材料参数并进行了仿真,结果表明,在截面面积相等时,圆形截面和矩形截面的振动频率分别为最低和最高,而末端变形正好相反,因此选择矩形截面可以减小变形;密度变化对柔性机械臂的变形程度影响不大,而弹性模量越大,振动频率越高,末端变形越小。滕悠优[57]分别针对机械臂大范围运动已知和未知的情况,对其末端附加质量位置及阻尼进行了研究。结果表明,在运动已知的情况下,机械臂末端的响应频率较低,阻尼影响很小;而在运动未知的情况下,在机械臂末端附加质量时,引起振幅变大,而响应频率降低,阻尼也对机械臂的振幅有所影响。因此,机械臂的系统参数对其动力学行为产生一定的影响,合理设计机械臂的结构及选择材料可以改善机械臂的工作性能,同时为机械臂系统的结构布置和主动抑振提供实验依据。
(3)关节驱动规律的确定。柔性机械臂的驱动力矩是机电转换的桥梁,为整个机械臂系统提供动力,机械臂在工作过程中,关节电机不断输出关节力矩,驱动关节转动到指定位置。由于机械臂关节驱动电机的大小、尺寸、质量等是有限的,因而产生的输出力矩也是有限的,而目前大部分研究是建立在驱动输入可以无限大的条件下来设计控制器的。对整个机械臂系统而言,过小的关节力矩不能保证关节运动,可能无法完成指定任务;而过大的关节力矩使转速过高,导致机械臂失稳、失控,甚至损坏电机。因此,合理选择关节力矩的范围,对提高机械臂的动力学性能、延长机械臂系统的寿命具有重要意义。
(4)柔性机械臂在高速运转下刚化与软化效应的分析。目前对柔性机械臂刚度变化问题的研究比较普遍,但往往忽略软化效应。综合考虑刚化效应和软化效应的影响,研究机械臂的刚度变化对其动力学特性的影响、建立时变刚度模型具有重要的理论价值。
(5)柔性机械臂关节精细建模。关节减速器包括行星齿轮减速器和谐波齿轮减速器,行星减速器的齿轮副间借助间隙发生相互作用,随着间隙的增大,机械臂的振动加剧,同时在运动过程中伴随着摩擦,影响机械臂的传动精度。而谐波减速器在传动过程中通过柔轮的可控变形传递扭矩,在大负载条件下,柔轮变形为非线性,柔轮与刚轮接触产生摩擦,严重影响机械臂的传动精度。机械臂在运动过程中,间隙和摩擦等非线性因素的影响复杂而不确定,研究其对机械臂传动精度的影响,建立较为精确的动力学模型,是振动主动抑制的关键,也是目前机械臂研究的重点与热点。
(6)空间柔性机械臂超低速运行时爬行现象的分析。摩擦力在机械臂中普遍存在,其对运动的影响大小不仅与动静摩擦因数有关,还与关节的传动刚度和传动速度密切相关。机械臂在超低速运转时,很容易出现爬行现象。爬行现象是一种很复杂的自激振现象,其主要原因是系统摩擦因数的变化和传动机构的刚度不足。爬行现象导致运行不稳定,严重影响机械臂的定位精度,甚至损坏传动系统,还会产生噪声。研究机械臂低速运转的爬行现象,考虑导致爬行的各种因素,是提高机械臂动力学性能的重要手段。柔性机械臂是集机、电、热一体化的系统,结构复杂,而且因对机械臂工作性能的要求越来越高,影响其动力学性能的因素也趋于多样化和复杂化。上述只是影响机械臂动力学行为的一些关键问题,要提高机械臂的动力学性能,还需要对机械臂系统进一步深入研究。另外,机械臂系统各部分关系密切,因此研究多种因素的耦合作用对机械臂动力学特性的影响也具有重要的意义。
5结论
虽然国内外对空间机械臂的研究取得了一定的进展,但仍有很多深层次的理论与技术问题有待进一步解决。
(1)在柔性机械臂动力学建模方面,如何确定机械臂的模态参数进而将其离散化是一个非常值得关注和研究的问题。另外,当前对机械臂的建模以单臂和双臂居多,对更多自由度机械臂系统的动力学模型研究相对较少,且很不完善。即使对单自由度机械臂进行建模,常常忽略关节非线性因素的影响,未整体考虑各部分因素的影响。
(2)在柔性机械臂刚度变化方面,建立时变刚度模型是今后研究的一个热点。
(3)在空间机械臂实验研究方面,机械臂是一个复杂的不确定系统,机械臂在运行过程中,各因素相互作用,因此考虑各种因素的综合影响是研究的一个重点。另外,实验系统与机械臂的实际工况仍有一定的差距,因此完善机械臂的实验系统,提高测量精度,对研究机械臂具有重要意义。
参考文献:
[1]刘明治, 刘春霞. 柔性机械臂动力学建模和控制研究[J]. 力学进展, 2001, 31(1):1-8.
LiuMingzhi,LiuChunxia.TheStudyonDynamicsModellingandControlofFlexibleMechanicalArms[J].AdvancesinMechanics, 2001, 31(1):1-8.
[2]于登云,孙京,马兴瑞.空间机械臂技术及发展建议[J].航天器工程,2007(4):1-8.
YuDengyun,SunJing,MaXingrui.SuggestiononDevelopmentofChineseSpaceManipulatorTechnology[J].SpacecraftEngineering,2007(4):1-8.
[3]王江勇,王基生,张俊俊,等.单自由度柔性机械臂刚柔耦合动力学仿真研究[J].机械设计与制造,2012(12):54-56.
WangJiangyong,WangJisheng,ZhangJunjun,etal.Rigid-flexibleCouplingDynamicSimulationResearchonaSingleDegreeofFreedomFlexibleManipulator[J].MachineryDesign&Manufacture, 2012(12):54-56.
[4]王树新, 员今天, 石菊荣,等. 柔性机械臂建模理论与控制方法研究综述[J]. 机器人, 2002, 24(1):86-91.
WangShuxin,YunJintian,ShiJurong,etal.ARoadmapofResearchonModelingandControlStrategyforFlexibleManipulators[J].Robot, 2002, 24(1):86-91.
[5]MuhammadAK,OkamotoS,LeeJH.ComparisonofProportional-derivativeandActive-forceControlsonVibrationofaFlexibleSingle-linkManipulatorUsingFinite-elementMethod[J].ArtificialLifeandRobotics, 2014, 19(4): 375-381.
[6]PirasG,CleghornW,MillsJ.DynamicFiniteElementAnalysisofaPlanarHigh-speed,High-precisionParallelManipulatorwithFlexibleLinks[J].MechanismandMachineTheory, 2005, 40(7): 849-862.
[7]ShawkyA,ZydekD,ElhalwagyYZ,etal.ModelingandNonlinearControlofaFlexible-linkManipulator[J].AppliedMathematicalModelling, 2013, 37(23): 9591-9602.
[8]王树新, 蒋铁英, 张铁民,等. 柔性机械臂的动力学分析与实验研究[J]. 中国机械工程, 1995,6(6):18-20.
WangShuxin,JiangTieying,ZhangTiemin,etal.DynamicAnalysisandExperimentalResearchofFlexibleManipulator[J].ChinaMechanicalEngineering,1995,6(6):18-20.
[9]李文龙,余正宁,师鹏,等.大范围运动柔性航天器的递推有限段法分析[J].中国空间科学技术,2012,32(4):22-28.
LiWenlong,YuZhengning,ShiPeng,etal.RecursiveFiniteSegmentMethodAnalysisofFlexibleSpacecraftUndergoingLargeOverallMotions[J].ChineseSpaceScienceandTechnology,2012,32(4):22-28.
[10]RahimiHN,NazemizadehM.DynamicAnalysisandIntelligentControlTechniquesforFlexibleManipulators:aReview[J].AdvancedRobotics, 2014, 28(2): 63-76.
[11]DingXilun.LumpedParameterDynamicModelingforTheflexibleManipulator[C]//FifthWorldCongressonIntelligentControlandAutomation.Hangzhou, 2004: 280-284.
[12]潘冬.空间柔性机械臂动力学建模分析及在轨抓捕控制[D].哈尔滨:哈尔滨工业大学,2014.
[13]ShabanaAA.DynamicsofMultibodySystems[M].Cambridge:CambridgeUniversityPress, 2013.
[14]SopanenJT,MikkolaAM.DescriptionofElasticForcesinAbsoluteNodalCoordinateFormulation[J].NonlinearDynamics, 2003,34(1/2): 53-74.
[15]杨敏, 刘克平. 柔性机械臂动力学建模与控制方法研究进展[J]. 长春工业大学学报:自然科学版, 2011, 32(1):7-13.
YangMin,LiuKeping.TheResearchAdvancesinModelingandControlMethodforFlexibleManipulator[J].JournalofChangchunUniversityofTechnology(NaturalScienceEdition), 2011, 32(1):7-13.
[16]霍伟.机器人动力学与控制[M].北京:高等教育出版社,2005.
[17]梁捷, 陈力. 双臂空间机器人基于高斯型函数的姿态、关节运动模糊自适应补偿控制[J].中国机械工程, 2010,21(3):330-336.
LiangJie,ChenLi.FuzzyAdaptiveCompensationControlforSpace-basedRobotSystemwithDual-armBasedonGaussian-typeFunctiontoTrackTrajectoryinJointSpace[J].ChinaMechanicalEngineering, 2010,21(3):330-336.
[18]KaneTR,LevinsonDA.FormulationofEquationsofMotionforComplexSpacecraft[J].JournalofGuidance,Control,andDynamics, 1980, 3(2): 99-112.
[19]刘延柱.基于高斯原理的多体系统动力学建模[J].力学学报,2014, 46(6): 940-945.
LiuYanzhu.DynamicModelingofMulti-bodySystemBasedonGauss’sPrinciple[J].ChineseJournalofTheoreticalandAppliedMechanics,2014,46(6):940-945.
[20]耿令波, 陈柏, 吴洪涛. 基于连接组合体方法的关节机器人动力学参数辨识[J]. 中国机械工程, 2014, 25(5):581-587.
GengLingbo,ChenBai,WuHongtao.IdentificationofArticulatedRobots’DynamicsParametersBasedonLinkage-assembliesMethod[J].ChinaMechanicalEngineering,2014, 25(5):581-587.
[21]于登云, 潘博, 孙京. 空间机械臂关节动力学建模与分析的研究进展[J]. 宇航学报, 2010,31(2):2448-2455.
YuDengyun,PanBo,SunJing.ALiteratureReviewonDynamicModelingandAnalysisoftheJointsinSpaceManipulator[J].JournalofAstronautics, 2010, 31(2):2448-2455.
[22]潘博, 于登云, 孙京. 大型空间机械臂关节动力学建模与分析研究[J]. 宇航学报, 2010, 31(11):2448-2455.
PanBo,YuDengyun,SunJing.ResearchonDynamicModelingandAnalysisofJointinLargeSpaceManipulator[J].JournalofAstronautics, 2010,31(11):2448-2455.
[23]MurotsuY,TsujioS,SendaKEI.DynamicsandPositioningControlofSpaceRobotwithFlexibleManipulators[C]//AIAAGuidance,NavigationandControlConference.Portland,OR, 1990: 735-742.
[24]KorayemMH,RahimiHN,NikoobinA.MathematicalModelingandTrajectoryPlanningofMobileManipulatorswithFlexibleLinksandJoints[J].AppliedMathematicalModelling, 2012, 36(7): 3229-3244.
[25]何柏岩,高峰,王树新.计及铰链间隙的机械臂动力学建模与仿真[J].天津大学学报,2005, 38(9):795-799.
HeBaiyan,GaoFeng,WangShuxin.ModelingandSimulationofaMechanicalArmwithJointClearance[J].JournalofTianjinUniversity,2005,38(9):795-799.
[26]ErkayaS.InvestigationofJointClearanceEffectsonWeldingRobotManipulators[J].RoboticsandComputer-IntegratedManufacturing, 2012, 28(4): 449-457.
[27]NamWK,OhSH.ADesignofSpeedReducerwithTrapezoidalToothProfileforRobotManipulator[J].JournalofMechanicalScienceandTechnology, 2011, 25(1): 171-176.
[28]ParkerRG,LinJ.Modeling,ModalProperties,andMeshStiffnessVariationInstabilitiesofPlanetaryGears[R].Columbus:OhioStateUniversityColumbusDepartmentofMechanicalEngineering, 2001.
[29]YangT,YanS,MaW.JointDynamicAnalysisofSpaceManipulatorwithPlanetaryGearTrainTransmission[J].Robotica, 2014,34(5):1-17.
[30]YangT,YanS.DynamicSimulationofPlanetaryGearbox[J].KeyEngineeringMaterials, 2014, 584:220-224.
[31]杨天夫,谷勇霞,阎绍泽.大型空间机械臂动力学建模及其性能分析[C]//中国空间科学学会2013年空间光学与机电技术研讨会.西安,2013:213-219.
[32]TuttleTD.UnderstandingandModelingtheBehaviorofaHarmonicDriveGearTransmission[R].Cambridge:MITArtificialIntelligenceLaboratory, 1992.
[33]谷勇霞,赵杰亮,阎绍泽,等.考虑谐波传动滞后的柔性空间机械臂运动精度[J].机械工程学报,2013,49(23):74-79.
GuYongxia,ZhaoJieliang,YanShaoze,etal.KinematicAccuracyoftheFlexibleSpaceManipulatorwithHarmonicDrive[J].JournalofMechanicalEnginnering, 2013,49(23):74-79.
[34]GomesSCP.DynamicModellingandFrictionCompensatedControlofaRobotManipulatorJoint[C]//Proceedingsof1992IEEEInternationalConferenceonRoboticsandAutomation.Nice, 1992: 1429-1435.
[35]金在权,权成七.弹性旋转梁的动力刚化效应[J].延边大学学报:自然科学版,2000,26(2):116-118.
JinZaiquan,QuanChengqi.TheStiffeningEffectoftheCentrifugalForce[J].JournalofYanbianUniversity(NaturalScience),2000,26(2):116-118.
[36]张俊苹.基于振动的旋转风力机叶片损伤识别研究[D].哈尔滨:哈尔滨工业大学,2012.
[37]于清, 洪嘉振. 柔性多体系统动力学的若干热点问题[J]. 力学进展, 1999(2):145-154.
YuQing,HongJiazhen.SomeTopicsonFlexibleMultibodySystemDynamic[J].AdvancesinMechanics, 1999(2):145-154.
[38]SimoJC,Vu-QuocL.OntheDynamicsofFlexibleBeamsunderLargeOverallMotions-thePlaneCase:PartII[J].JournalofAppliedMechanics, 1986, 53(4): 855-863.
[39]deBorstR,CrisfieldMA,RemmersJJC,etal.NonlinearFiniteElementAnalysisofSolidsandStructures[M].WestSussex:JohnWiley&Sons, 2012.
[40]SharfI.GeometricallyNon-linearBeamelementforDynamicsSimulationofMultibodySystems[J].InternationalJournalforNumericalMethodsinEngineering, 1996, 39(5): 763-786.
[41]陆念力,张宏生.一种高精度几何非线性递推凝聚梁单元[J].中国工程机械学报,2008,6(1):1-5.
LuNianli,ZhangHongsheng.InvestigationintoHigh-accuracyGeometrically-nonlinearRecursiveCondensationBeamElement[J].ChineseJournalofConstructionMachinery,2008,6(1):1-5.
[42]阎绍泽,季林红,范晋伟,等.柔性机械系统动力学的变形耦合方法[J].机械工程学报,2001,37(8):1-4.
YanShaoze,JiLinhong,FanJinwei,etal.Deformation-CouplingModelingMethodforDynamicsofFlexibleMechanicalSystems[J].ChineseJournalofMechanicalEngineering, 2001,37(8):1-4.
[43]LeungAYT.DynamicSubstructureMethodforElasticFractalStructures[J].Computers&Structures, 2011, 89(3): 302-315.
[44]吴胜宝, 章定国. 大范围运动刚体-柔性梁刚柔耦合动力学分析[J]. 振动工程学报, 2011, 24(1):1-7.
WuShengbao,ZhangDingguo.Rigid-flexibleCouplingDynamicAnalysisofHub-flexibleBeamwithLargeOverallMotion[J].JournalofVibrationEngineering,2011, 24(1):1-7.
[45]YangT,YanS,HanZ.NonlinearModelofSpaceManipulatorJointConsideringTime-variantStiffnessandBacklash[J].JournalofSoundandVibration, 2015, 341: 246-259.
[46]杨康华.柔性机械臂的振动控制与实验研究[D].北京:北京邮电大学,2011.
[47]余跃庆,周刚,方道星.基于模糊PID融合的柔性机械臂振动压电主动控制研究[J].中国机械工程, 2008,19(15):1836-1841.
YuYueqing,ZhouGang,FangDaoxing.ActiveVibrationControlforFlexiblePiezoeletricManipulatorBasedonFuzzy-PIDFusionControl[J].ChinaMechanicalEngineering, 2008,19(15):1836-1841.
[48]阎绍泽,季林红,刘才山,等.柔性机械臂结构-控制藕合特征的实验研究[J].机械科学与技术,2000,19(5):796-798.
YanShaoze,JiLinhong,LiuCaishan,etal.OntheStructure-controlInteractionofFlexibleManipulators[J].MechanicalScienceandTechnology, 2000,19(5):796-798.
[49]张令波,孙富春,孙增圻.基于云模型的柔性机械臂轨迹跟踪与振动抑制控制[C]//2005年中国智能自动化会议论文集.南京, 2005:342-347.
[50]GreenwoodDT.PrinciplesofDynamics[M].EnglewoodCliffs,NJ:Prentice-Hall, 1988.
[51]周留栓, 贾庆轩, 张晓东.机器人一体化关节性能测试系统的设计与实现[J]. 机电产品开发与创新, 2007, 20(5):1-3.
ZhouLiushuan,JiaQingxuan,ZhangXiaodong.Design&ImplementationofPerformance-testingSystemforRobotModularJoint[J].Development&InnovationofMachinery&ElectronicProducts, 2007,20(5):1-3.
[52]SunH,JiaQ,PingY.DevelopmentofaGeneral2-DOFSpaceModule[C]// 2006IEEE/RSJInternationalConferenceonIntelligentRobotsandSystems.Beijing:IEEE, 2006:1002-1007.
[53]李成, 梁斌. 空间机器人的遥操作[J]. 宇航学报, 2004, 22(1):95-98.
LiCheng,LiangBin.TeleoperationofSpaceRobotics[J].JournalofAstronautics,2001,22(1):95-98.
[54]SkeltonRE,YousuffA.ComponentCostAnalysisofLargeScaleSystems[J].InternationalJournalofControl, 1983, 37(2): 285-304.
[55]唐国潮,金国光,刘远.柔性机械臂动力学建模及特性研究[J].机械科学与技术, 2009,28(8):1031-1034.
TangGuochao,JinGuoguang,LiuYuan.ResearchofDynamicModelingandPerformanceforRigid-FlexibleManipulator[J].MechanicalScienceandTechnologyforAerospaceEngineering, 2009,28(8):1031-1034.
[56]郭振锋,金国光,畅博彦,等.刚-柔性机械臂动力学建模及其动力学特性研究[J].天津工业大学学报, 2013,32(1):70-74.
GuoZhenfeng,JinGuoguang,ChangBoyan,etal.ResearchofDynamicModelingandPerformanceforRigid-flexiblemanipulator[J].JournalofTianijnPolytechnicUniversity,2013,32(1):70-74.
[57]滕悠优. 柔性机械臂的主动控制与实验研究[D]. 上海:上海交通大学, 2007.
(编辑袁兴玲)
收稿日期:2016-01-05
基金项目:高等学校博士学科点专项科研基金资助项目(20120002110070);国家自然科学基金资助项目(11272171)
中图分类号:TP24
DOI:10.3969/j.issn.1004-132X.2016.12.024
作者简介:谷勇霞,女,1968年生。北京工商大学材料与机械工程学院副教授。主要研究方向为机械设计及机械系统动力学。张玉玲,女,1989年生。北京工商大学材料与机械工程学院硕士研究生。赵杰亮,男,1989年生。清华大学摩擦学国家重点实验室博士研究生。阎绍泽,男,1964年生。清华大学摩擦学国家重点实验室教授、博士研究生导师。
AdvancesonDynamicsModelingandExperimentalStudiesforFlexibleManipulators
GuYongxia1ZhangYuling1ZhaoJieliang2YanShaoze2
1.BeijingTechnologyandBusinessUniversity,Beijing,100048 2.StateKeyLaboratoryofTribology,TsinghuaUniversity,Beijing,100084
Abstract:This paper summarized the latest advances on the flexible manipulator modeling theories and relevant experiments of scholars at home and abroad, systematically expounded the study status of the methods to describe the flexible manipulator deformations, the joint dynamics modeling, the dynamic modeling methods of flexible manipulator systems, the stiffening and softening effects of the arms and the experimental methods. Then this paper proposed the present problems and shortcomings of manipulator dynamics theory and experimental study, predicted the main direction and core technology of the flexible manipulator dynamics research and analyzed key technical problems about the optimal mode order selection of flexible manipulators in detail. The system parameter optimization based on the dynamic characteristics of flexible manipulators, the determination of joint driving laws, the stiffening and softening effects of manipulator arms under high speed, the fine modeling of flexible manipulator joints and the crawling phenomenon in the super low speed of space flexible manipulators were presented.
Key words:flexible manipulator; dynamics modeling; stiffness change; experimental study

